Завдання для індивідуальної роботи "Логарифмічні рівняння"


1. Логарифмічні рівняння, які розв’язуються за допомогою означення
логарифма.
Ми знаємо, що logaN=α, aα=N, де α – любе дійсне число, N – число що
логарифмується, N >0, α – основа логарифма, причому α>0, α≠1.
Розв’язати рівняння.
- log3(1-2x)=1
-
log
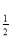 (-
(-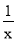 )=4
)=4
- log3(x-12)=2
-
log
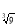 x=1,5
x=1,5
-
log x
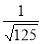 =-1,5
=-1,5
-
3
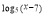 =log464
=log464
-
3
 =log7343
=log7343
- 0,1lg(36-4x)=lg1010
-
2
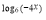 =log381
=log381
- 3log4(-5x)=log5125
- xlgx=0
- logx2401=4
- lg(x-2)2=0
-
logx(
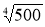 )3=-
)3=-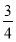
- 2log4(z-8,5)=log381
-
logx8
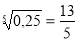
- log7 log3log2log2x=0
-
log8log2log2log2
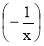 =0
=0
-
log11log3log2
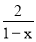 =0
=0
-
2lg
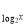 2=1
2=1
-
logx225=
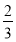
- logx2401=4
- logx0,125=1,25
-
log
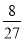 x=
x=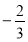
-
10
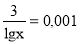
-
2
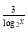 =
=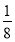
-
4
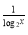 =2
=2
-
log
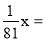 1,25
1,25
-
log27x=-
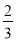
2. Рівняння першого степеня відносно логарифма, які розв’зуються
потенціюванням.
Перехід від рівності, що містить логарифм, до рівності, що не містить його
називається потенціюванням. При розв’язанні таких рівнянь використовуємо
основні логарифмічні тотожності: теорему, що коли логарифми рівні, то при
рівних основах області дійсних чисел рівні і числа, що логарифмуються.
Розв’зати рівняння.
- lgx-lg11= lg19- lg (30-x).
-
5lgx-lg288=3lg
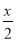
- lg (x+2)-lg5= lg (x-6).
- lg(7x-9)2+lg(3x+4)2=2.
- lgx=2-lg5.
-
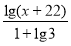 =2.
=2.
-
lg (x+6)-
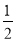 lg (2x -3)=2-lg25.
lg (2x -3)=2-lg25.
-
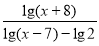 =2.
=2.
-
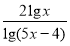 =1.
=1.
-
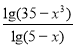 =3.
=3.
-
lg(2x+x-13)=x-xlg5.

-
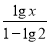 =2.
=2.
- 3lg(x+4,8)+lg5=272lg2.
- lgx-1(x2-5x+10) =2.
-
lg(
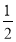 +x)=lg
+x)=lg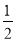 - lgx.
- lgx.
- 2lgx=-lg (6-x2).
-
0,5lg(2x-1)+lg
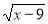 =1.
=1.
- 100lg (x+20) =10000.
-
lg 9-1+ xlg
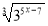 =0
=0
-
logx3-logx2=
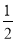
- log4 (x+3)-log4 (x-1)=2-log48
-
log2 (x-1)+log2(x+1)=
=3log22+log2(x-2). - lg3x-1=2 (lg21+lg2)-lg7
-
lg3+
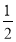 lg (y-22)=lg
lg (y-22)=lg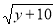 .
.
-
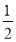 lg(99x2+
lg(99x2+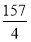 )-1=lg (x+
)-1=lg (x+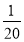 )
)
- log2 (9-2x) =x=3
- xlog23-1=-log 218.
- lg (2x+1) +x =xlg5+lg6.
- lg (x-1)3-3lg (x-3)=lg8
- log2 (2x-3) +x=2


про публікацію авторської розробки
Додати розробку
