Відділ освіти виконавчого комітету 

Дунаєвецької селищної ради

Навчально-виховний комплекс 

«Морозівська загальноосвітня школа І-ІІІ ступенів - дошкільний навчальний заклад»

Розгонюк О.М.

Завдання для контролю  знань учнів з алгебри 9 клас

   2019 р.

Автор: Розгонюк Оксана Миколаївна, вчитель математики НВК «Морозівська ЗОШ  І-ІІІ ст. –ДНЗ»

Рецензент: Сікора Микола Миколайович, методист управління освіти, молоді і спорту Дунаєвецької міської ради

Схвалено до друку науково-методичною радою  методичного кабінету  управління освіти, молоді та спорту  Дунаєвецької міської ради

 (протокол №1  від 26.102.2019 року)

ПЕРЕДМОВА

Посібник містить завдання для поточного та тематичного оцінювання учнів 9 класу з алгебри за програмою з математики  для 5-9 класів загальноосвітніх навчальних закладів та розроблені до підручника Г.П.Бевз, В.Г.Бевз  «Алгебра, 9 клас».

Неодмінною рисою посібника є наявність різноманітних завдань для контролю знань учнів 9 класу з алгебри. 

Запропоновані завдання призначені для проведення самостійних та контрольних робіт  за темами «Нерівності», «Квадратична функція».

Даний посібник допоможе вчителеві здійснити ефективний контроль над рівнем засвоєння навчального матеріалу, а учневі – зорієнтуватися у завданнях та набути навичок швидкого та безпомилкового виконання  робіт.

Умовні позначення:

КЗ – контроль знань

СР – самостійна робота

КЗ 1. Загальні відомості про нерівності

Варіант 1

1. Вкажіть серед наведених числових нерівностей правильні:

            1)        5)2√3 < 3√2.

2. Порівняйте числа a і b, якщо:

         1) 𝑎 − 𝑏 = 2,7;                  2)  .

3. Порівняйте значення виразів 5𝑥 − 1 і 4𝑥 + 1, якщо:

          1) 𝑥 = 0;                           2)  .

4. Підберіть три натуральних числа y, які задовольняють нерівність:

         1) 𝑦 + 3 ≥ 0;                      2) .

5. Дано числа a, b, c, d, e. Відомо, що 𝑑 < 𝑐, 𝑎 > 𝑐, 𝑏 > 𝑒, 𝑒 > 𝑎.

1)    Зобразіть на числовій прямій задані числа.

2)    Запишіть задані числа в порядку зростання.

3)    Знайдіть серед заданих чисел найменше.

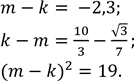6. Порівняйте, коли це можливо, числа m і k, якщо: 1)

2)

3)

КЗ 1. Загальні відомості про нерівності

Варіант 2

1. Вкажіть нерівності, які при 𝑥 = 2,5 є правильними:

         1) 4𝑥 + 1 ≥ 9;           2) −8𝑥 + 20 ≤ 0;

3) .

2. Порівняйте числа a і b, якщо:

            1)                2) 𝑏 + 3 = 𝑎 + 1.

3. Порівняйте значення виразів 5𝑥 − 1 і 4𝑥 + 1, якщо:

         1)  𝑥 = 2;                            2)  𝑥 = 2,5.

4. Підберіть три натуральних числа y, які задовольняють нерівність:

         1) 3 − 𝑦 ≥ 0;                      2) 1 + 2𝑦 ≤ 7.

5. Дано числа a, b, c, d, e. Відомо, що 𝑑 < 𝑐, 𝑎 > 𝑐, 𝑏 > 𝑒, 𝑒 > 𝑎.

1)    Зобразіть на числовій прямій задані числа.

2)    Запишіть задані числа в порядку спадання.

3)    Знайдіть серед заданих чисел найбільше.

6. Порівняйте, коли це можливо, числа m і k, якщо:

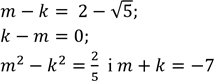1)

2)

3). 

КЗ 2. Властивості числових нерівностей

Варіант 1

1.     Додайте до обох частин нерівності −17 + 𝑥 < 12  число 17.

2.     Відніміть від обох частин нерівності −23 + 𝑥 < −11 число −23.

3.     Перенесіть доданки зі змінною в ліву частину, а числа – у праву частину нерівності: 23 + 𝑥 ≥ −5𝑥 − 16.

4.     Виконайте множення або ділення обох частин нерівності відповідно до запису:

1);

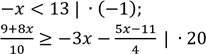2)

3).

5.     Виконайте додавання нерівностей:

1) 𝑎 < 3 𝑖 𝑛 < 6; 2).

6.     Відомо, що 𝑏 < 𝑘 Порівняйте вирази:

1)    5 + 𝑏 𝑖 5 + 𝑘;

2)    −5𝑏 𝑖 − 5𝑘;

3)    .

КЗ 2. Властивості числових нерівностей

Варіант 2

1.     Додайте до обох частин нерівності 𝑥 + 8 < 13  число –8.

2.     Відніміть від обох частин нерівності 15 + 𝑥 ≥ −5 число 15.

3.     Перенесіть доданки зі змінною в ліву частину, а числа – у праву частину нерівності: −13 − 4𝑥 ≥ −12𝑥 + 34.

4.     Виконайте множення або ділення обох частин нерівності відповідно до запису:

1);

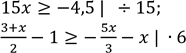2)

3).

5. Виконайте додавання нерівностей:

1)    𝑏 > −10 𝑖 𝑥 > −12;

2)    .

6. Відомо, що 𝑏 < 𝑘 Порівняйте вирази:

1)    −𝑏 𝑖 − 𝑘;

2)    4𝑏 𝑖 4𝑘;

3)    .

КЗ 3. Подвійні нерівності

Варіант 1

Запишіть у вигляді подвійної нерівності співвідношення: 1) 𝑥 < 17 𝑖 𝑥 > 0;

2) 𝑥 < 5 𝑖 𝑥 > 0.

2. Знайдіть цілі значення y, які задовольняють нерівність:

1)    −2 < 𝑦 < 2;

2)    −1 < 𝑦 ≤ 3.

3. Оцініть значення виразів   2𝑚; 2𝑚 + 3; −𝑚; 1 − 𝑚, якщо:

1)    1 < 𝑚 < 3;

2)    −3 < 𝑚 < 4.

4. Оцініть значення виразів , якщо:

1)    −9 < 𝑚 < 15;

2)    −3,6 < 𝑚 < −1,8.

5.     Відомо, що 6 < 𝑎 < 7, 12 < 𝑐 < 18. Оцініть значення виразу:

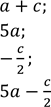1)

2)

3)

4).

6.     Вантажна машина перевозить 𝑏 тонн вантажу, причому  4,6 ≤ 𝑏 ≤ 6,2.  Оцініть загальну масу вантажу, який можуть перевезти 10 таких машин.

КЗ 3. Подвійні нерівності

Варіант 2

Запишіть у вигляді подвійної нерівності співвідношення: 1) 𝑥 ≥ −0,1 𝑖 𝑥 ≤ 0,1;

2) 𝑥 < 9 𝑖 𝑥 ≥ 0.

2. Знайдіть цілі значення y, які задовольняють нерівність:

1)    −3 < 𝑦 < 3;

2)    −4 ≤ 𝑦 ≤ 5.

3. Оцініть значення виразів   2𝑚; 2𝑚 + 3; −𝑚; 1 − 𝑚, якщо:

1)    2 < 𝑚 < 5;

2)    −2 < 𝑚 < 6.

4. Оцініть значення виразів , якщо:

1)    −6 < 𝑚 < 12;

2)    −5,4 < 𝑚 < −2,1.

5. Відомо, що 2 < 𝑎 < 10, 4 < 𝑐 < 25. Оцініть значення виразу:

1)

2)

3)

4)

6. Маса 𝑚 однієї шоколадної цукерки набуває значень  19,8 ≤ 𝑚 ≤ 20,2 (у грамах). Оцініть у грамах масу всіх шоколадних цукерок у 10 коробках, якщо одна коробка містить 30 таких цукерок.

КЗ 4. Розв’язування нерівностей з однією змінною

Варіант 1

Розв’яжіть нерівність:

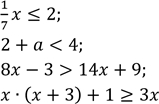1)

2)

3)

4).

2.     Знайдіть область допустимих значень змінної виразу:

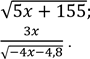1)

2)

3.     Розв’яжіть нерівність. У відповідь запишіть усі натуральні розв’язки цієї нерівності.

.

4.     Утворіть за умовою завдання нерівність і розв’яжіть її:

1)    За яких значень змінної  𝑡 двочлен 25 + 3𝑡 набуває від’ємних значень?

2)    За яких натуральних парних значень змінної 𝑎 значення виразу 5(3𝑎 − 4) + 7(2𝑎 − 11) не більше за подвоєне значення суми 10𝑎 + 3?

КЗ 4. Розв’язування нерівностей з однією змінною Варіант 2

Розв’яжіть нерівність:

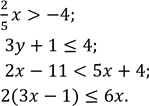1)

2)

3)

4)

2.     Знайдіть область допустимих значень змінної виразу:

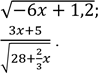3)

4)

3.     Розв’яжіть нерівність. У відповідь запишіть усі натуральні розв’язки цієї нерівності.

.

4.     Утворіть за умовою завдання нерівність і розв’яжіть її:

1)    За яких значень змінної  𝑚 значення виразу 0,4𝑚 − 2  не менше, ніж значення двочлена   −0,6𝑚 − 11 ?

2)    За яких значень змінної 𝑦 двочлен 5𝑦 − 1,1 набуває значень, більших за 3,9?

КЗ 5. Об’єднання і переріз множин. Числові проміжки

Варіант 1

Зобразіть на числовій прямій задані проміжки, знайдіть їх переріз та запишіть відповідь.

1)    [4; +∞)і [0; 6];

2)    (−∞; 11) і [−4; 7);  3) (−∞; 10) і [10; +∞).

2.     Зобразіть на числовій прямій задані проміжки, знайдіть їх об’єднання та запишіть відповідь. 1) (5; +∞) 𝑖 (7; +∞;

2) [−6; 11] 𝑖 [12; 16]; 3) (−∞; 13) 𝑖 [13; +∞).

3.     Зобразіть на числовій прямій множину чисел, які задовольняють кожну з нерівностей.

1)    𝑥 ≤ 1 𝑖 − 11 ≤ 𝑥 < 6;

2)    𝑥 < 6 𝑖 − 9 < 𝑥 ≤ 3.

4.     Знайдіть переріз та об’єднання проміжків [2; 15) 𝑖 (−2; 8) та вкажіть найбільше натуральне число з об’єднання  проміжків, якщо воно існує.

5.     Запишіть у вигляді проміжку множину точок, зображену на рисунку.

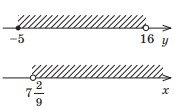
1)  

2)

6.     Визначте, чи є задане число  розв’язком нерівності:

1)    𝑥 > −9, 𝑥₀ = 0; 2) 3𝑥 + 17 < 0, 𝑥₀ = 1.

КЗ 5. Об’єднання і переріз множин. Числові проміжки Варіант 2

Зобразіть на числовій прямій задані проміжки, знайдіть їх переріз та запишіть відповідь.

4) [−2; 10] і (−11; 5); 5) (−3; 5) і [2; +∞);  

6) (−∞; 6] і [6; +∞) .

2.     Зобразіть на числовій прямій задані проміжки, знайдіть їх об’єднання та запишіть відповідь.

4)    (−∞; 2] 𝑖 (−∞; 5];

5)    (2; 7] 𝑖 [5; 11]; 6) (−∞; 11) 𝑖  (10; +∞).

3.     Зобразіть на числовій прямій множину чисел, які задовольняють кожну з нерівностей. 3) 𝑥 > 2 𝑖 − 7 < 𝑥 ≤ 4;

4)    𝑥 ≥ 4 𝑖 5 ≤ 𝑥 < 12.

4.     Знайдіть переріз та об’єднання проміжків   (−11; 6] 𝑖 (−6; 7) та вкажіть найменше ціле число з перерізу проміжків, якщо воно існує.

5.     Запишіть у вигляді проміжку множину точок, зображену на рисунку.

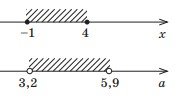1)  

2)

6.     Визначте, чи є задане число  розв’язком нерівності:

3) 𝑥 < 14, 𝑥₀ = −5; 4) 17 − 4𝑥 ≥ 0, 𝑥₀ = 4.

КЗ 6. Системи нерівностей з однією змінною

Варіант 1

Визначте, чи є число 3 розв’язком системи нерівностей:

 . 

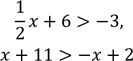2.     Розв’яжіть систему нерівностей:

  𝑥 < 0, 𝑥 < −5,

         𝑥 ≤ 7.

3.     Розв’яжіть систему нерівностей:

,

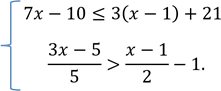4.     Розв’яжіть нерівність:

1)    −4 < 𝑥 ≤ 6 − 𝑥;

2)    −15 < 𝑥 − 4 ≤ 11 − 2𝑥.

КЗ 6. Системи нерівностей з однією змінною

Варіант 2

Визначте, чи є число 10 розв’язком системи нерівностей:

 . 

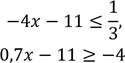2.     Розв’яжіть систему нерівностей:

  𝑥 < −3, 𝑥 ≤ −2,

         𝑥 > 6.

3.     Розв’яжіть систему нерівностей:

,

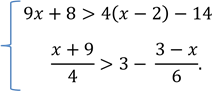4.     Розв’яжіть нерівність:

1)    2 − 𝑥 ≤ 𝑥 < 9;

2)    17 − 3𝑥 ≤ 𝑥 + 5 < 21.

КЗ 7. Доведення нерівностей

Варіант 1

Доведіть твердження:

якщо 𝑎 − 𝑏 ≥ √3, 𝑎 + 𝑏 ≥ 11√3, то 𝑎² − 𝑏² ≥ 33.

2.     Доведіть нерівність за умови, що 𝑎 ≥ 0, 𝑏 ≥ 0, 𝑐 ≥ 0.

(𝑎² + 4)(𝑏² + 4) ≥ 16𝑎𝑏.

3.     Доведіть нерівність, якщо  x - довільне дійсне число.

1) 4𝑥² ≥ 12𝑥 − 9; 2) 3(𝑎 + 8) > 2(𝑎 + 4) + 𝑎.

4.     Доведіть, що квадрат суми двох довільних дійсних чисел не менший від їх добутку, помноженого на 4.

5.     Доведіть нерівність, якщо число 𝑎 ≥ 0:

.  

6.     Доведіть нерівність, якщо  a i b  - невід’ємні дійсні числа:

.

КЗ 7. Доведення нерівностей

Варіант 2

Доведіть твердження: якщо .

2.     Доведіть нерівність за умови, що 𝑎 ≥ 0, 𝑏 ≥ 0, 𝑐 ≥ 0.

(𝑎² + 9)(𝑏² + 9) ≥ 36𝑎𝑏.

3.     Доведіть нерівність, якщо  x - довільне дійсне число.

1)    16𝑥² ≥ 8𝑥 − 1; 2) 4(𝑥 − 3) < 3(𝑥 + 1) + 𝑥.

4.     Доведіть, що сума квадратів двох довільних дійсних чисел не менша від їх добутку, помноженого на  −2.

5.     Доведіть нерівність, якщо число 𝑎 ≥ 0:

.  

6.     Доведіть нерівність, якщо  a i b  − невід’ємні дійсні числа:

.

КЗ 8. Функція

Варіант 1

Знайдіть значення функції при заданих значеннях аргументу:

                 𝑦(𝑎) = 2𝑎² + 𝑎,          𝑎 = −2.

2.     Знайдіть значення аргументу при заданому значенні функції:

                 𝑦 = 𝑥² − 3𝑥 + 7,          𝑦 = 11.

3.     Не виконуючи побудови графіка, визначте, чи проходить через задану точку графік функції:

.

4.     Знайдіть область визначення функції  .

5.     Не виконуючи побудови, знайдіть координати точок перетину графіків функцій

𝑦 = −𝑥² + 4𝑥 𝑖 𝑦 = 2𝑥.

6.     Зобразіть, як може виглядати графік функції, область визначення якої 𝐷(𝑦) = (−∞; −2) ∪ (−2; 2) ∪ (2; +∞).

КЗ 8. Функція

Варіант 2

Знайдіть значення функції при заданих значеннях аргументу:

                 𝑠(𝑡) = 𝑡² − 4,           𝑡 = −5.

2.     Знайдіть значення аргументу при заданому значенні функції:

.

3.     Не виконуючи побудови графіка, визначте, чи проходить через задану точку графік функції:

.

4.     Знайдіть область визначення функції  .

5.     Не виконуючи побудови, знайдіть координати точок перетину графіків функцій

𝑦 = 𝑥² + 2 𝑖 𝑦 = 𝑥 + 2.

6.     Зобразіть, як може виглядати графік функції, область визначення якої 𝐷(𝑦) = (−∞; −2) ∪ (2; +∞).

КЗ 9. Властивості функцій

Варіант 1

1)    Знайдіть нулі функції:

1)    𝑦 = 6 − 18𝑥;

2)    𝑦 = 4 + 3𝑥 − 𝑥².

2)    Доведіть, що функція 𝑦(𝑥) зростає на заданому проміжку:

𝑦 = 𝑥² + 6𝑥, [−3; +∞).

3) 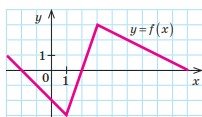   За графіком функції 𝑦 = 𝑓(𝑥),  заданої на проміжку  [-3;9] (див.рис.), знайдіть: 1) 𝑓(3), 𝑓(1), 𝑓(0), 𝑓(9);  

2)    нулі функції;

3)    область значень функції;

4)    множину розв’язків нерівності 𝑓(𝑥) ≤ 0;  

5)    множину розв’язків нерівності 𝑓(𝑥) ≥ 0.

4)    На рисунку зображено графік, що ілюструє залежність обсягу споживання гарячої води (у л/год) протягом однієї доби в певному житловому будинку від часу (у год). 

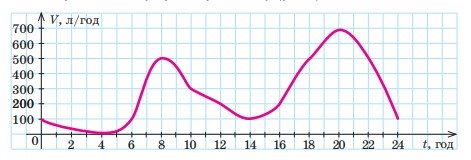
1)    Яке значення обсягу споживання гарячої води (у л/год) спостерігалось о

16.00?

2)    Яким був найбільший обсяг споживання гарячої води (у л/год) протягом доби? О котрій годині це спостерігалось?

3)    Яким був найменший обсяг споживання гарячої води (у л/год) протягом доби? О котрій годині це спостерігалось?

4)    Вкажіть проміжки часу (у год), протягом яких обсяг споживання гарячої води збільшувався. 

КЗ 9. Властивості функцій

Варіант 2

1.     Знайдіть нулі функції:

1)    𝑦 = 42 + 7𝑥;

2)    𝑦 = 𝑥² + 𝑥 − 6.

2.     Доведіть, що функція 𝑦(𝑥) спадає на заданому проміжку:

.

3. 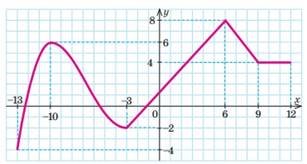    За графіком функції 𝑦 = 𝑓(𝑥),  заданої на проміжку  [-13;12] (див.рис.), знайдіть:

1)𝑓(−13), 𝑓(−3), 𝑓(6), 𝑓(12);  

2)         нулі функції;

3)         область значень функції;

4)         множину розв’язків нерівності 𝑓(𝑥) ≤ 0;  

5)         множину розв’язків нерівності

𝑓(𝑥) ≥ 0.

4.     На рисунку точками позначено щомісячну кількість запитів у пошуковій системі Google від користувачів певної країни щодо методів профілактики та лікування грипу (у відсотках від загальної кількості інтернет-користувачів цієї країни).

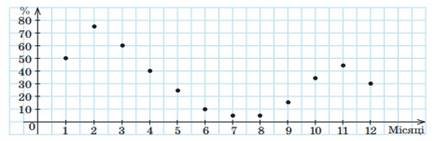
1)    Який відсоток користувачів зафіксовано пошуковою системою в листопаді?

2)    Якою була максимальна кількість запитів (у %) у пошуковій системі протягом року? У якому місяці це було зафіксовано?

3)    Якою була мінімальна кількість запитів (у %) у пошуковій системі протягом року? У якому місяці це було зафіксовано?

4)    Якщо кількість запитів перевищує 60%, то розглядається питання про запровадження карантину в навчальних закладах. В яких місяцях порушувалось це питання?

КЗ 10. Перетворення графіків функцій

Варіант 1

1. Знайдіть координати точки, у яку переміститься точка А(4; -3) графіка функції

𝑦 = 𝑓(𝑥), якщо внаслідок його перетворення отримали графік функції:

1)    𝑦 = 𝑓(𝑥) + 2;

2)    𝑦 = 𝑓(𝑥 − 5);

3)    𝑦 = −6𝑓(𝑥).

2.     Дано графік функції  Графік якої функції отримаємо, якщо перенесемо заданий графік: 1) вниз на  3 одиниці; 2)вправо на 7 одиниць?

3.     При яких a  точка А (a; 36) належить графіку функції

4.     Побудуйте графік функції  𝑦 = 2 − (𝑥 − 1)²   та знайдіть за графіком:

1) область значень функції;  2) нулі функції; 3) проміжки знакосталості; 4) проміжки зростання і спадання функції; 5) найбільше, найменше значення функції.

5. 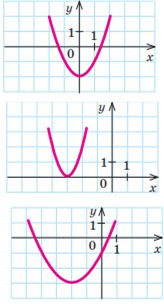    За рисунками, на яких зображено фрагменти графіків функцій, фрагменти графіків функцій 𝑦 = 𝑓(𝑥),  знайдіть:

1)    значення a, якщо 𝑦 = 𝑥² + 𝑎;

2)    значення a і b, якщо 𝑦 = 𝑏(𝑥 + 𝑎)²;

3)    значення a, b і c, якщо 𝑦 = 𝑏(𝑥 + 𝑎)² + 𝑐. 

КЗ 10. Перетворення графіків функцій

Варіант 2

1)    Знайдіть координати точки, у яку переміститься точка А(-2; 1) графіка функції 𝑦 = 𝑓(𝑥), якщо внаслідок його перетворення отримали графік функції:

1)     

2)    𝑦 = 𝑓(𝑥 + 4);

3)    𝑦 = 3𝑓(𝑥).

2)    Дано графік функції  Графік якої функції отримаємо, якщо перенесемо заданий графік: 1) вгору на 2 одиниці; 2) вліво на 5 одиниць?

3)    При яких a точка А (a; 36) належить графіку функції 𝑦 = −12𝑥?

4)    Побудуйте графік функції  𝑦 = −(𝑥 − 1)² + 4   та знайдіть за графіком: 1) область значень функції;  2) нулі функції; 3) проміжки знакосталості; 4) проміжки зростання і спадання функції; 5) найбільше, найменше значення функції.

5) 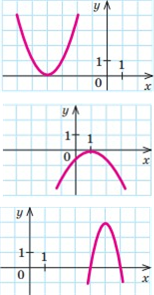   За рисунками, на яких зображено фрагменти графіків функцій, фрагменти графіків функцій 𝑦 = 𝑓(𝑥),  знайдіть:

1)    значення a, якщо 𝑦 = (𝑥 + 𝑎)²;  

2)    значення a і b, якщо 𝑦 = 𝑏(𝑥 + 𝑎)²;  

3)    значення a, b і c, якщо 𝑦 = 𝑏(𝑥 + 𝑎)² + 𝑐. 

КЗ 11. Квадратична функція

Варіант 1

1. 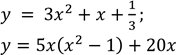    Визначте, чи є квадратичною функція 𝑦(𝑥), якщо: 1)

2).

2.     Знайдіть значення квадратичної функції 𝑓(𝑥) в точці 𝑥₀ , якщо:

𝑓(𝑥) = −2𝑥² + 𝑥 − 5,   𝑥₀ = −1.

3.     Знайдіть координати (𝑥₀; 𝑦₀) вершини параболи 𝑦 = 3𝑥² − 6𝑥 + 5.

4.     Знайдіть значення невідомих коефіцієнтів, при яких графік  заданої квадратичної функції проходить через вказані точки. Запишіть формулу, якою задано функцію. Дослідіть функцію за алгоритмом та побудуйте її графік, якщо:

𝑦 = −𝑥² + 4𝑥 + 𝑐,   𝐴(−3; −9).

5.     Струмінь води музичного фонтану є параболою, яку можна описати рівнянням

𝑦 = 𝑎𝑥² + 𝑏𝑥, 𝑥 ∈ [0; 4]. Знайдіть значення коефіцієнтів a і b, якщо відомо, що

𝑦(4) = 0  і вода піднімається на найбільшу висоту 3 м, тобто 𝑦(2) = 3.

КЗ 11. Квадратична функція

Варіант 2

1. Визначте, чи є квадратичною функція 𝑦(𝑥), якщо:

1);

2).

2.     Знайдіть значення квадратичної функції 𝑓(𝑥) в точці 𝑥₀ , якщо:

𝑓(𝑥) = 𝑥² − 6𝑥 + 1,   𝑥₀ = 0.

3.     Знайдіть координати (𝑥₀; 𝑦₀) вершини параболи 𝑦 = 𝑥² − 2𝑥 − 8.

4.     Знайдіть значення невідомих коефіцієнтів, при яких графік  заданої квадратичної функції проходить через вказані точки. Запишіть формулу, якою задано функцію. Дослідіть функцію за алгоритмом та побудуйте її графік, якщо:

𝑦 = 𝑥² + 2𝑥 + 𝑐,   𝐴(2; −16).

5.     Футболіст б’є по нерухомому м’ячу в напрямку суперника. Траєкторія польоту м’яча може бути змодельована графіком функції

відстань (у м) по горизонталі від футболіста (точки удару) до м’яча, 𝑦 − висота (у м), на яку піднімається м’яч над полем. Визначте, на яку найбільшу висоту піднявся м’яч над футбольним полем.

КЗ 12. Квадратні нерівності

Варіант 1

1.     За рисунками, на яких зображено графіки квадратичних функцій 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐, знайдіть значення x, що задовольняють задану умову.

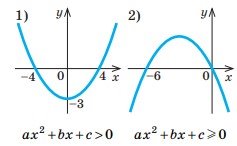
2.     Розв’яжіть графічним способом нерівність:

1)    1 − 𝑥² ≤ 0;

2)    𝑥² − 4𝑥 < 12.

3.     Зведіть задану нерівність до рівносильної нерівності з додатним старшим коефіцієнтом:

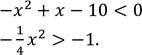1),

2)

4.     Розв’яжіть аналітичним способом нерівність:

1)    (𝑥 + 3)(𝑥 − 7) < 0,

2)    𝑥(𝑥 + 1) + 2 < 2(1 − 𝑥).

5.     Знайдіть область визначення функції:

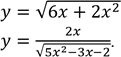1)

2)

6.     Розв’яжіть систему нерівностей:

.

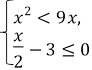КЗ 12. Квадратні нерівності

Варіант 2

1.     За допомогою графіка розв’яжіть нерівність:

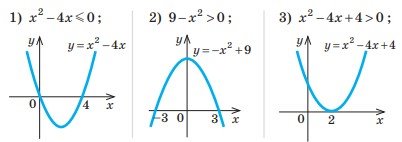
2.     Розв’яжіть графічним способом нерівність:

1)    𝑥² − 9 < 0;

2)    𝑥² − 2𝑥 + 1 > 0.

3.     Зведіть задану нерівність до рівносильної нерівності з додатним старшим коефіцієнтом:

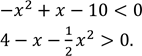1),

2)

4.     Розв’яжіть аналітичним способом нерівність:

1)    (2𝑥 + 5)(3𝑥 − 4) ≤ 0,

2)    𝑥(𝑥 + 14) < 7(2𝑥 + 14).

5. 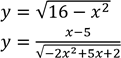    Знайдіть область визначення функції: 3)

4).

6.     Розв’яжіть систему нерівностей:

,

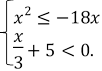КЗ 13. Системи рівнянь другого степеня

Варіант 1

Визначте, чи є наведені пари чисел розв’язками заданої системи рівнянь:

2𝑥 + 𝑦 = 3, 𝑥² + 𝑦² = 5

1) (−2; 1) 2) (2; −4).

2.     Розв’яжіть графічним способом систему рівнянь: 

𝑥² + 𝑦² = 5,

2𝑦 − 𝑥 = 0

3.     Розв’яжіть систему рівнянь:

𝑥² + 𝑥𝑦 = 5, 𝑦² + 𝑥𝑦 = 20

4.     Розв’яжіть систему рівнянь:

,

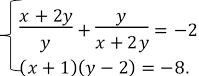5.     Знайдіть значення m, при яких система рівнянь має єдиний розв’язок:

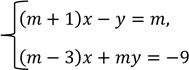
КЗ 13. Системи рівнянь другого степеня

Варіант 2

Визначте, чи є наведені пари чисел розв’язками заданої системи рівнянь:

𝑦 = 𝑥², 𝑥² − 𝑦² = 0

1) (2; 1) 2) (−1; 1).

2.     Розв’яжіть графічним способом систему рівнянь: 

𝑥² + 𝑦² = 5,

2𝑦 + 𝑥 = 0

3.     Розв’яжіть систему рівнянь:

𝑥² + 2𝑥𝑦 = 55,

𝑥² − 2𝑥𝑦 = −5

4.     Розв’яжіть систему рівнянь:

. 

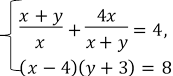5.     Знайдіть значення m, при яких система рівнянь має безліч розв’язків:

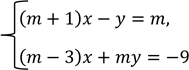
КЗ 14. Розв’язування задач складанням систем рівнянь

Варіант 1

Аудиторія містила x рядів по y місць у кожному. Під час реконструкції до кожного ряду додали по одному місцю, і загальна кількість місць в аудиторії збільшилася від 40 до 48. Запишіть систему рівнянь для визначення x і y.

Знайдіть x і y.

2.     У першому будинку 36 квартир, а в другому – 50. У другому будинку поверхів на 2 менше, а квартир на кожному поверсі на 2 більше, ніж у першому будинку. Знайдіть кількість поверхів у кожному будинку та кількість квартир на кожному поверсі.

3.     Кожна з двох бригад має оновити інформацію на 24 бігбордах. Перша бригада щогодини оновлювала x бігбордів, друга бригада – y бігбордів. Відомо, що перша бригада щогодини встигала оновити на 1 бігборд більше, ніж друга, і закінчила роботу на 2 год раніше від неї. Запишіть систему рівнянь для визначення x і y. Знайдіть x і y.

4.     Для проведення відбіркового туру з розв’язування логічних задач підготували 400 аркушів паперу. Кожний учасник мав одержати однакову кількість аркушів для написання роботи. Оскільки 20 учасників не з’явилися, то кожному учаснику видали на 1 аркуш більше, ніж планувалося.

1)    Скільки учасників прийшли на відбірковий тур?

2)    Скільки аркушів планували видавати кожному учаснику?

КЗ 14. Розв’язування задач складанням систем рівнянь

Варіант 2

Площа прямокутника дорівнює 36 см². Якщо його ширину зменшити на 1 см, а довжину збільшити на 1 см, то його площа дорівнюватиме 30 см². Складіть систему рівнянь для визначення ширини і довжини прямокутника та знайдіть їх. 

2.     Дві бригади, що здійснюють роботи з утеплення фасадів, працюючи разом, виконують усе завдання за 6 год. За скільки годин може виконати це завдання кожна бригада, працюючи самостійно, якщо одній бригаді на це потрібно на 5 год більше, ніж іншій бригаді?

3.     Перший менеджер має оформити 80 замовлень, а другий – 56 таких самих замовлень. Перий менеджер оформлював щогодини на 2 замовлення більше, ніж другий, а закінчив свою роботу на 1 год пізніше, ніж другий. Скільки замовлень оформлював кожний менеджер щогодини? 

4.     На першому друкарському верстаті можна виконати всю роботу на 3 год швидше, ніж на другому. Якщо на першому верстаті працювати лише 4 год,  а потім виконувати завдання лише на другому верстаті, то знадобиться ще 3 год, щоб закінчити все завдання. 

1)    Нехай усе завдання можна виконати на першому верстаті за x год, на другому – за y год. Запишіть систему рівнянь для визначення x та y.

2)    Знайдіть x та y.

СР 1. Загальні відомості про нерівності

1.     Вкажіть нерівність, що є правильною, якщо m – будь-яке дійсне число.

                А. 𝑚 + 1 ≥ 0                            Б. 2𝑚 ≥ 0  

                 В. 𝑚² ≥ 0                       Г. 𝑚 − 1 ≤ 0.

2.     Оцініть значення виразу 2𝑥, якщо −4 < 𝑥 < 6. А. −8 < 2𝑥 < 12      Б.−2 < 2𝑥 < 3  В. −2 < 2𝑥 < 8                       Г.−6 < 2𝑥 < 4.

3.     Відомо, що −3 < 𝑦 < 9. Оцініть значення виразу 1 − 𝑦.

                 А. −2 < 1 − 𝑦 < 10                Б. −4 < 1 − 𝑦 < 8

                 В. −8 < 1 − 𝑦 < 4         Г. −9 < 1 − 𝑦 < 3

4.     Вкажіть нерівність, яка є правильною для всіх дійсних чисел с.

                А. 𝑐 − 4 > 𝑐 − 3            Б. 𝑐 − 2 > 𝑐 − 1

                В. 3 + 𝑐 > 4 + 𝑐            Г. 2 + 𝑐 > 1 + 𝑐.

5.     Галина завжди прибирає свою кімнату не менше ніж за 30 хв. Вчора дівчина впоралася за t хв. Якому числу може дорівнювати t?  А. 36 Б. 25  В.  10               Г. 8.

6.     Встановіть відповідність між твердженням (1 – 3) та виразом (А – Г), для якого це твердження є правильним.

1)    Значення виразу більш за нуль 

                        для всіх дійсних чисел a                               А. 4𝑎 + (𝑎 − 2)² − 𝑎² − 4

2)    Значення виразу менше від нуля  для всіх дійсних чисел a Б. 𝑎(𝑎 + 4) − 𝑎² + 2     

3)    Значення виразу дорівнює нулю  для всіх дійсних чисел a В. 4𝑎 + 𝑎² − (𝑎 + 2)²      

                                         Г. 𝑎(𝑎 − 4) + 4𝑎 + 2.  

7.     Підлога хореографічної зали має форму квадрата. Довжина b сторони цього квадрата задовольняє нерівність 19,5 < 𝑏 < 20,1  (у м).

1)    Оцініть периметр цього квадрата (у м).

2)    Оцініть периметр підлоги іншої хореографічної зали квадратної форми (у м), сторона якої втричі більша.

8.     Доведіть нерівність якщо 𝑥 ≥ 0.

СР 2. Властивості числових нерівностей  

1)    Відомо, що 6 < 𝑚 < ^[1] і  2 < 𝑛 < 3. Оцініть значення виразу 𝑚 + 𝑛.

                 А. 8 < 𝑚 + 𝑛 < 11                   Б. 9 < 𝑚 + 𝑛 < 10

В. 12 < 𝑚 + 𝑛 < 24 Г. 8 < 𝑚 + 𝑛 < 12

2)    Відомо, що 5 < 𝑎 < 9 і  1 < 𝑏 < 4. Оцініть значення виразу 𝑎 − 𝑏. А. −5 < 𝑎 − 𝑏 < −4            Б. −8 < 𝑎 − 𝑏 < −1  

В. 1 < 𝑎 − 𝑏 < 8 Г. 4 < 𝑎 − 𝑏 < 5

3)    Відомо, що 4 < 𝑝 < 7. Оцініть значення виразу . А.                       Б.  

                   В.                              Г.  

4)    Відомо, що 4 < 𝑝 < 10 і  2 < 𝑞 < 6. Оцініть значення виразу .

                   А.                 Б.   

                   В.                    Г.   

5)    Ціна 1 кг картоплі не менша від 7 грн і не більша за 9 грн. Тарас за 8 кг картоплі заплатив m грн. Вкажіть число, яке може бути значенням m. 

                 А. 55                                     Б. 60

                 В.  75                                      Г. 80.

6)    Відомо, що 10 < 𝑥 < 100 і  2 < 𝑦 < 5. Встановіть відповідність між початком речення (1 – 3) та  його закінченням (А – Г) так, щоб утворилося правильне твердження.

1)    Значення виразу 𝑥𝑦                                       А. більше за 0,02 і менше від 0,5 2) Значення виразу ^𝑥                                          Б. більше за 20 і менше від 500 

𝑦

3) Значення виразу                                           В.більше за 0,2 і менше від 5 

                                                                              Г. більше за 2 і менше від 50  

7)    Майстер виготовляє дерев’яні декоративні дощечки прямокутної форми. Ширина такого прямокутника становить a см, 10 ≤ 𝑎 ≤ 20, довжина – b см, 15 ≤ 𝑏 ≤ 30.

1)    Оцініть площу S (у см²) цього прямокутника.

2)    Оцініть периметр P (у см) цього прямокутника.

СР 3. Розв’язування  нерівностей з однією змінною

1.     Вкажіть число, що є розв’язком нерівності 𝑥 > −14.

                А. −10                                     Б.−14

В. −18 Г. −25  

2.     Розв’яжіть нерівність 3𝑥 ≥ 15.

                А. (−∞; 12]                              Б. (−∞; 5]  

В. [5; +∞) Г. [12; +∞)

3.     Розв’яжіть нерівність 6 − 𝑥 ≥ 0.

А. [6; +∞)       Б. (−∞; −6]

                В. [−6; +∞)                             Г. (−∞; 6]

4. 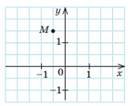    На рисунку зображено точку 𝑀(𝑥₀; 𝑦₀) на координатній площині. Вкажіть проміжок, якому належить число 𝑦₀. А. (−∞; −1) Б. (1; +∞)  

                В. (−1; 0)                                 Г. (0; 1) 

5.     Перед показом фільму тривалістю 120 хв транслюють рекламний блок із x роликів по 2 хв кожний. Кожний фільм разом із рекламою має тривати не більше ніж 130 хв. Вкажіть нерівність для визначення x. 

                 А. 2𝑥 + 120 ≥ 130                Б. 𝑥 + 120 ≤ 130

                 В. 2𝑥 + 120 ≤ 130      Г. 𝑥 + 120 ≥ 130.

6.     Встановіть відповідність між проміжками (1 – 3) та  їх зображеннями (А – Г) на числовій прямій.  

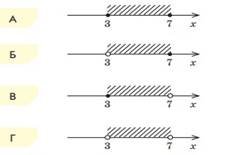
1)       [3; 7)                                        

2)       (3; 7)                                                         

3)       (3; 7]                

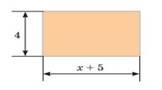7. На рисунку зображено схему ділянки прямокутної форми, призначеної для облаштування автобусної зупинки. Площа ділянки не повинна перевищувати 48м².

1)    Запишіть нерівність для визначення x.

2)    Знайдіть усі можливі натуральні значення x.  

8)    Розв’яжіть нерівність  Запишіть усі натуральні розв’язки цієї нерівності. 

СР 4. Розв’язування нерівностей з однією змінною

1.     Розв’яжіть подвійну нерівність −6 ≤ 2𝑥 ≤ 10.

А. [−4; 12] Б. [−8; 8]

В. [−3; 5] Г. [−12; 20]

2.     Розв’яжіть подвійну нерівність −12 ≤ 𝑥 − 4 ≤ 20.

                А. [−16; 16]                             Б. [−3; 5]  

В. [−8; 24] Г. [−5; 3]

3.     Знайдіть об’єднання проміжків (1;4) і (3;9). А. (1; 9)                                Б. (4; 9)

                В. (3; 4)                                    Г. (1; 3)

4.     Розв’яжіть систему нерівностей

,

                А. (−∞; −3) ∪ (4; +∞)           Б. (−3; 4)  

                В. (4; +∞)                                Г. ∅

5.     До участі в конкурсі на кращий соціальний плакат запрошують молодь. За умовами конкурсу вік учасників x становить від 15 до 35 років. Вкажіть систему нерівностей для визначення x. 

 А. 𝑥 ≥ 15,          Б. 𝑥 ≤ 15,

      𝑥 ≤ 35 𝑥 ≥ 35

 В.  𝑥 ≤ 15,           Г. 𝑥 ≥ 15       𝑥 ≤ 35                 𝑥 ≥ 35.

6.     Встановіть відповідність між нерівностями (1 – 3) та  множинами їх розв’язків 

(А – Г).  

7.     Розв’яжіть нерівність 19 − 4𝑥 ≤ 𝑥 + 4 < 11.

8.     Розв’яжіть систему нерівностей  

.

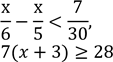СР 5. Функції. Властивості функцій

1.     Функцію задано формулою  Знайдіть 𝑦(−1).

                А. 1                               Б. 3  

                В.  −3                             Г. −1.

2.     Знайдіть      значення     аргументу, при    якому          значення     функції       𝑦 = 3 + дорівнює 7.

А. 0 Б.16  В.  2                Г.4.

3.     Знайдіть нулі функції 𝑦 = 𝑥² − 36.

                А. −18; 18                               Б. 18

                В. 6                                         Г. −6; 6.

4.     На рисунку подано графік функції 𝑦 = 𝑓(𝑥). Знайдіть її область визначення.

                А. [−1; 7]                                 Б. [2; 6]

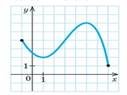                В. [−1; 6]                                Г. [1; 5].

5.     Чайка полює на рибу, іноді пірнаючи під воду. На рисунку зображено залежність відстані h між чайкою та поверхнею води від часу t.  Додатні значення h відповідають висоті польоту чайки над водою, від’ємні – глибині, на яку вона пірнає. Вкажіть проміжок часу, протягом якого чайка була під водою.

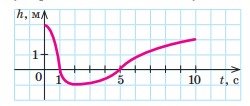                 А. (0; 1)                                 Б. (1; 5)

                 В. (0; 2)                                 Г.(−1; 0).

6.     Встановіть відповідність між заданою функцією (1 – 3) та областю її визначення (А – Г).

𝑥

1)

2)  𝑦 = √𝑥 − 1;       Б. (−∞; 1) ∪ (1; +∞)

3)  𝑦 = √1 − 𝑥;       В.[1; +∞)                       

                                       Г. (1; +∞). 

7.     Визначте проміжки знакосталості функції .

8.     Знайдіть область визначення функції .

СР 6. Функції. Властивості функцій

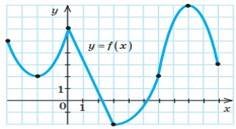
Завдання 1-5. Функція 𝑦 = 𝑓(𝑥), яку задано графічно, визначена на проміжку [−4; 10] (див.рис.)

1.     За рисунком знайдіть найбільше значення функції 𝑦 = 𝑓(𝑥) на проміжку [0; 3].

А. −2 Б. 3  В.  6            Г. 8.

2.     За рисунком знайдіть найменше значення функції 𝑦 = 𝑓(𝑥) на проміжку [6; 10].

                А. −2                                     Б.2

                В.  3                            Г.8.

3.     За рисунком знайдіть найбільше значення функції 𝑦 = 𝑓(𝑥) на області її визначення.

А. 5            Б. 6 В.  8 Г. 10.

4.     За рисунком знайдіть найменше значення функції 𝑦 = 𝑓(𝑥) на області її визначення.

А. −2                              Б. 2 В. 3                                        Г. −4.

5.     Серед поданих проміжків виберіть такий, на якому функція 𝑦 = 𝑓(𝑥) зростає 

А. [−4; 0]              Б. [0; 8] В. [8; 10]              Г. [3; 6].

6.     Встановіть відповідність між початком речення (1 – 3) та його закінченням (А – Г) так, щоб утворилося правильне твердження.

1)    Функція 𝑦 = 2 − 𝑥              А. не має нулів

2)    Функція 𝑦 = 𝑥 − 2 Б. спадає на проміжку  (−∞; +∞)

3)    Функція 𝑦 = 2                    В. має два нулі                          

Г. зростає на проміжку (−∞; +∞).

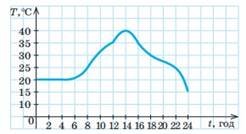7. На рисунку зображено графік зміни температури T повітря (у ⁰С) протягом однієї доби. 

1)    Якою була найвища температура повітря протягом цієї доби? О котрій годині вона спостерігалася?

2)    У приміщенні встановлено кондиціонер. Він автоматично        вмикається,      як      тільки

температура повітря на вулиці перевищує 25⁰С, та вимикається, якщо температура повітря на вулиці стає нижчою від 25⁰С. Визначте проміжок часу, протягом якого кондиціонер працював.

         8. Доведіть, що функція ¹ спадає на проміжку (1; +∞).

СР 7. Перетворення графіків функцій

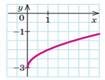
Вкажіть функцію, графік якої може бути зображений на рисунку.

                              А.                   Б.

                    В.  +3;                         Г.

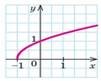
2.     Вкажіть функцію, графік якої може бути зображений на рисунку.  

                              А.                   Б.

                          В.                                         Г.

3.     Вкажіть функцію, графік якої може бути зображений на рисунку.

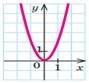                   А.                           Б.𝑦 = −2𝑥²;  

                           В.                          Г. 𝑦 = 2𝑥².

4.     Проміжок [0; 1] є областю значень функції 𝑦 = 𝑓(𝑥). Знайдіть область значень функції 𝑦 = 𝑓(𝑥) + 2.

А. [2; 3]; Б. [0; 2];  В. [−2; −1];                 Г. [0; 3].

5.     Машина для вишивання запрограмована відтворювати орнамент, визначений функцією 𝑦 = 𝑓(𝑥) (див.рис.). Яка  функція зображає орнамент, який проходить через точку М?

                  А. 𝑦 = 𝑓(𝑥) − 2                       Б.𝑦 = 𝑓(𝑥) + 1;  

                 В.  𝑦 = 𝑓(𝑥 + 1);                     Г.𝑦 = 𝑓(𝑥 − 1).

6.     Встановіть відповідність між функціями (1 – 3) та алгоритмами (А – Г) побудови їх графіків за допомогою геометричних перетворень.

1)            А. Графік функції паралельно перенести на 

                                        6 одиниць вліво вздовж осі 𝑂𝑥

2)            Б. Графік функції паралельно перенести на 

                                        6 одиниць вправо вздовж осі 𝑂𝑥

3)                    В. Графік функції паралельно перенести на 

                                        6 одиниць вниз вздовж осі 𝑂𝑦

                        Г. Графік функції паралельно перенести на 

                                        6 одиниць вгору вздовж осі 𝑂𝑦.

7.     Використовуючи графік функції 𝑦 = 𝑥², побудуйте графік функції 𝑦 = 3𝑥² − 2.

8.     Визначте графічним способом кількість коренів рівняння .

СР 8. Квадратична функція, її властивості

Вкажіть проміжок, на якому функція 𝑦 = (𝑥 − 4)² зростає.

                А. [−4; +∞);                            Б.[4; +∞);  

                В. (−∞; 4];                               Г. (−∞; −4].

2.     Знайдіть область значень функції 𝑦 = (𝑥 − 1)² + 2. А. (−∞; 1];             Б.(−∞; 2];  В.  [1; +∞); Г.[2; +∞).

3.     Знайдіть координати точки перетину графіка функції 𝑦 = 𝑥² − 6𝑥 + 9  з віссю

Оу.

А. (0; 9); Б.(9; 0);  В.  (0; 3);                         Г. (3; 0).

4.     Визначте нулі функції 𝑦 = 𝑥² − 4𝑥 − 5.

А. 5; 1                                        Б. 5; −1 В. −5; 1                                Г. −5; −1.

5.     Вітки параболи 𝑦 = 𝑎𝑥² − 7𝑥 + 2 напрямлені вниз. Яке з чисел може бути значенням коефіцієнта 𝑎? А. √3                          Б.

                           В.                                   Г. 3

6.     Встановіть відповідність між формулою, якою задано квадратичну функцію  (1

– 3) та абсцисою вершини її графіка (А – Г).

1)              𝑦 = (𝑥 − 5)² − 1;              А. 𝑥_в = −5 

2)              𝑦 = 5 + (𝑥 − 1)²;              Б. 𝑥_в = −1

3)              𝑦 = 𝑥² + 10𝑥 + 1;                      В. 𝑥_в = 1

                        Г. 𝑥_в = 5

7. Змоделюємо рух акробата під час стрибка. Приймемо спортсмена за матеріальну очку. Траєкторію його польоту можна змоделювати графіком функції Місце, з якого акробат стрибнув, є початком координат. Тоді x – відстань (у м) по горизонталі між поточним положенням точки й початком координат, y – відстань (у м) по вертикалі від підлоги спортзалу (висота, на якій перебуває матеріальна точка).

1)              Побудуйте графік заданої функції, якщо 𝑥𝜖 [0; 4]. 

2)              Визначте, на яку найбільшу висоту піднявся акробат під час стрибка.

8. Задано квадратичну функцію 𝑦 = 𝑥² + 𝑏𝑥 + 8.  Знайдіть значення  b, при якому графік цієї функції проходить через точку 𝑀(−1; 3),  і запишіть формулу, якою задано функцію.

СР 9. Квадратні нерівності

Використовуючи фрагмент графіка функції 𝑦 = −0,5𝑥² + 4𝑥 − 6, зображений на рисунку, розв’яжіть нерівність  −0,5𝑥² + 4𝑥 − 6 ≥ 0.  А. (−∞; 4];             Б.[2; 6];  

В. (−∞; 2] ∪ [6; +∞); Г. [0; 2].

2.     Розв’яжіть нерівність  𝑥² + 5𝑥 − 6 < 0.

А. (−6; 1);                       Б.(−∞; −1) ∪ (6; +∞);  В. (−1; 6);                          Г.(−∞; −6) ∪ (1; +∞).

3.     Розв’яжіть нерівність (𝑥 − 3)(𝑥 + 5) ≥ 0.

А. [−5; 3]; Б.(−∞; −3] ∪ [5; +∞);  В. [−3; 5];                         Г.(−∞; −5] ∪ [3; +∞).

4.     Розв’яжіть нерівність 𝑥² − 49 > 0.

А. (−∞; 7)               Б. (−∞; −7) ∪ (7; +∞)  В. (7; +∞)                 Г. (−7; 7).

5.     Розв’яжіть нерівність 𝑥² − 𝑥 + 2 ≥ 0.

 А. ∅ Б.  (−∞; −1] ∪ [2; +∞) В.  [−1; 2] Г. (−∞; +∞).

6.     Встановіть відповідність між заданою нерівністю  (1 – 3) та кількістю (А – Г) всіх її цілих розв’язків.

7.     За допомогою спеціального пристрою м’ячик підкинули вертикально вгору з поверхні землі. Висота (у м) м’ячика  над землею змінюється за законом ℎ(𝑡) = −5𝑡² + 16𝑡,   де t – час (у с), що пройшов із моменту кидка (t = 0).

1)    Через скільки секунд після кидка м’ячик опиниться на землі?

2)    Вкажіть проміжок часу ( у с), протягом якого висота м’ячика над землею була більшою за 11 м.

8. Розв’яжіть систему нерівностей 

𝑥² + 3𝑥 − 18 ≤ 0,

           𝑥 + 5 > 0.

СР 10. Системи рівнянь другого степеня

Яка з наведених пар чисел є розв’язком системи рівнянь 𝑥 − 𝑦 = 5, 𝑥𝑦 = −4?

                А. (1; 4)                                    Б.(1; −4)  

В. (−4; 1) Г. (4; 1).

2.     У рівнянні     зроблено заміну ^𝑥        𝑡. Яке рівняння одержали?

                  А.                                Б.

                В. 𝑡 + 3𝑡 = 4                      Г.

3.     Розв’яжіть систему рівнянь  𝑦 = 2𝑥,

𝑥² + 𝑦² = 5.

               А. (2; 1), (−2; −1)                            Б. (1; 2), (−1; 2)  

               В. (1; 2), (1; −2)                                Г. (1; 2), (−1; −2).

4.     Знайдіть значення m, при якому система рівнянь має безліч розв’язків:

𝑚𝑥 + 𝑦 = 5,

2𝑥 + 𝑦 = 5

                А. Таких значень не існує                 Б. 𝑚 = 1  

                В. 𝑚 = 2                                             Г. 𝑚 = 5.

5.     Знайдіть усі значення m, при яких система рівнянь має єдиний розв’язок: 𝑥 + 𝑦 = 1, 

3𝑥 + 𝑚𝑦 = 2

А.      1 Б.          ≠ ¹  В. 𝑚 ≠ 2                                       Г. 𝑚 ≠ 3.

6.     Використовуючи графік рівняння 𝑥² + 𝑦² = 4, встановіть відповідність між системо рівнянь 3) та кількістю (А – Г) її розв’язків.

1)            𝑥            + 𝑦     = 4,              А. Жодного

   𝑦 = 𝑥  

2)            𝑥² + 𝑦² = 4,              Б. Один

3)            𝑥            + 𝑦     = 4,              В. Два

                        Г. Більше ніж два

7.     На рисунку у прямокутній системі координат зображено схеми маршрутів двох круїзних океанських лайнерів. Маршрути є графіками рівнянь 𝑥 − 𝑦 = 2 і 𝑥² −

2𝑥 − 𝑦 = 2. Визначте координати точок перетину цих маршрутів (див рис.)  

8.     Розв’яжіть систему рівнянь 𝑥² + 𝑥𝑦 = −7,

𝑦² + 𝑥𝑦 = 5

СР 11. Розв’язування задач складанням систем рівнянь

У кінотеатрі x рядів, у кожному ряді 10 місць. Скільки всього місць у кінотеатрі?

𝑥

А.                                   Б.10𝑥  10

В.                                            Г. 𝑥 + 10.

2.     Величина x більша за величину y на 6. Виразіть x через y.

                А. 𝑥 = 𝑦 + 6                             Б. 𝑥 = 𝑦 − 6

                 В. 𝑥 = 6𝑦                                    Г.

3.     Для фарбування x м² підлоги витрачається y л фарби. Скільки літрів фарби потрібно для фарбування підлоги площею 5𝑥 м²? А. 5𝑦                          Б.  

                В.                                               Г.     

𝑦

4.     Катер рухався проти течії річки протягом 3 год. Яку відстань пройшов катер, якщо його власна швидкість дорівнює y км/год, а швидкість течії річки – x км/год?

А. 3𝑥𝑦                            Б. 3(𝑥 + 𝑦)  В. 3(𝑦 − 𝑥)                           Г. 3(𝑥 − 𝑦).

5.     Довжина гіпотенузи прямокутного трикутника дорівнює 4 см, один із катетів на 1 см менший, ніж другий. Яка система рівнянь відповідає умові, якщо довжину меншого катета позначено через x см, а більшого – через y см?

                  А. 𝑥 − 𝑦 = 1,                Б.     𝑥 − 𝑦 = 1,

      𝑥² + 𝑦² = 4     𝑥² + 𝑦² = 16                 

                 В. 𝑦 − 𝑥 = 1,      Г.   𝑦 − 𝑥 = 1

𝑥² + 𝑦² = 4                    𝑥² + 𝑦² = 16                  

6.     Встановіть відповідність між задачами  (1 – 3) та виразами (А – Г), що є розв’язками задач.

1)      Потяг проїхав x км зі швидкістю y км/год                               А.            Скільки годин потяг був в дорозі? 2)       З басейну об’ємом y л викачали воду за x год.                     Б. ^𝑥

𝑦

                              Скільки літрів води викачували з басейну щогодини?          

3)              Автобус за один рейс перевозить x пасажирів. В. 𝑥 + 𝑦

          Скільки пасажирів перевіз автобус, здійснивши y рейсів?

Г. 𝑥𝑦              

7.     Різниця чисел x і y дорівнює 5, а їх добуток дорівнює 14. Запишіть систему рівнянь для визначення x і y. Розв’яжіть систему.

8.     Два дизайнери, працюючи разом, виконують завдання за . Одному дизайнеру на виконання цього завдання потрібно на 1 год більше, ніж іншому. За скільки годин може виконати завдання кожен дизайнер, працюючи самостійно?

Контрольна робота  №1

Числові нерівності

Варіант І

Частина І (1 бал за завдання)

1.     Відомо, що а < b. Яке твердження є неправильним?

А) а-3 > b-3;   Б) 3а < 3b;

В) -3a > -3b;   Г) a+3 < b+3.

2.     Порівняйте числа m і n, якщо m – n = -3,5.

А) mn;   Б) mn;   

В) m > n;   Г) m<n.

3.     Додайте нерівності 4<8 , 2<6.

А) 6<14   Б) 614   

В) 6>14   Г) 614

4.     Розмістіть числа у порядку зростання: -4,2; -2,4; -3,6.

А) -4,2; -2,4; -3,6;     Б) -2,4; -3,6; -4,2;      

В) -3,6; -4,2; -2,4;      Г) -4,2; -3,6; -2,4

5.     Знайдіть добуток нерівностей 0,5  < 6 і  4 < 5.

А) 2 ≤ 3;    Б) 20 < 30;   

В) 2 < 30;    Г) 2 > 3.

Частина ІІ ( по 2 бали)

6.     Відомо, що а < b. Порівняйте вирази: 2а + 7 і 2b + 9.

7.     Оцініть значення виразу 3a-4b, якщо 4,2<a<4,3 і 1,0<b<1,2

Частина ІІІ (3 бали )

8.     Відомо, що 9<n<10 і 3<m<6. Оцініть значення виразу m² : n.

Контрольна робота  №1

Числові нерівності

Варіант ІІ

Частина І (1 бал за завдання)

1.   Відомо, що k > p. Яке твердження є правильним?

А) 5k < 5p ;  Б) k-5 < p-5;   

В) k-5 > p-5;   Г)-5k > -5p.

2.   Порівняйте числа a і b, якщо a –b = -5 А) a>b; Б) a<b;   В) ab;   Г) ab.

3.   Знайдіть добуток нерівностей 7>3, _ .

А) 51   Б) 51    

В) 5>1     Г) 5<1.

4.   Розмістите числа у порядку зростання: 0; -3,9; 0,2.

А) 0; 0,2; 3,9   Б) 0,2; 0; -3,9   

В) -3,9; 0; 0,2   Г) -3,9; 0,2; 0

5.   Додайте нерівності 0,5 < 6 і 4 < 5.

А) 9 < 14;        Б) 4,5 ≤ 11;     

В) 4,5 < 11;    Г) 4,5 > 11.  

Частина ІІ. (2 бали)

6.   Відомо, що а > b. Порівняйте вирази:  3-a  і  3 – b.

7.   Оцініть значення виразу 2y-x, якщо 2<x<3 і 9<y<14.

Частина ІІІ. (3 бали )

8.   Відомо, що 3 < х < 6 і 1 < у < 9. Оцініть значення виразу  х² : у.

Контрольна робота  №2

Лінійні нерівності з однією змінною

Варіант І

Частина І (1 бал за завдання)

1.   Який з проміжків є розв’язком нерівності 6x 48;

А) x;8 ; Б) x8; ; 

В) x8; ;Г) x;8 . 

2.   Розв’яжіть нерівність 4х-3 < 2х+7.

А) x;5 ; Б) x5; ;

 В) x5; ;Г) x;5 . 

x 2,

3.Яке число є розв’язком системи нерівностей          

_2x 50

А) 1;   Б) 30 ;  В) 12;   Г) 25.

4.   Розв’яжіть систему нерівностей і вкажіть її найбільший цілий розв’язок

2 x 6,

           

_ 2x10

А) 3;   Б) 4;   В) -5;   Г) -6. 

5.   Знайдіть допустимі значення змінних: √х + 3

А) (−3; +∞) ;    Б) [-3;+∞);    В)  (-∞;-3) ;     Г)(-∞;-3].

Частина ІІ (2 бали).

6.   Розв’яжіть нерівність   -

7.   Розв’яжіть нерівність 5x17 13x2

Частина ІІІ (4 бали)

8.   Розв’яжіть систему нерівностей 2x13  52x1 7x

_3x1 2  61x 7x

Контрольна робота №2

Лінійні нерівності з однією змінною

Варіант ІІ

Частина І (1 бал за завдання)

1.   Який з проміжків є розв’язком нерівності 7x35

А) x;5 ; Б) x5; ; 

В) x5; ; Г) x;5  .

2.   Розв’яжіть нерівність 5-3х<17-5х.

А) x;6;      Б) x6; ; 

В) x6;; Г) x;6 . 

x13,

3.Яке число є розв’язком системи нерівностей           

_2x 6

А) 3;   Б) 4;   В) 2;   Г) -15 .

4.   Розв’яжіть систему нерівностей і вкажіть її найбільший цілий розв’язок

x3 5,

             

_0,5x 3

А) 6;   Б) 5;   В) -2;   Г) -1. 

5.   Знайдіть допустимі значення змінних:  

А) (2; +∞) ;    Б) [2;+∞);    В)  (-∞;2) ;     Г)(-∞;2].

Частина ІІ (2 бали).

6.   Розв’яжіть нерівність   -

7.   Розв’яжіть нерівність 4a87a112

Частина ІІІ (4 бали)

5x1x 2x 2

8.   Розв’яжіть систему нерівностей _        

_4x1 2  22x1x

Контрольна робота №3

Квадратична функція та її графік

Варіант І І частина ( за кожне завдання 1 бал)

1.   Яка з функцій є квадратичною?

А) у = 3х -4;   Б) у = х + 3;

В) у = √х + 3; Г) у = х² + 3х – 4.

2.   Знайдіть координати вершини параболи у = х² − 8х + 12.

А)  (-4;-4);   Б)  (4;4);   

В)  (4;-4);   Г)  (-4;4).

3.   Знайдіть значення функції  f(х) = в точці х₀ = -14.

А) 8;    Б) -1;   В)  13;    Г) 4.

4.   При якому значенні х невизначена функція у =   ? 

А) 4;   Б) 1; 4;    В) -1; -4;   Г) -4.

5.   Знайдіть нулі функції у = х∙(7х-1).

А)  0;       .

ІІ частина (за завдання – 2 бали)

6.   Розв’яжіть нерівність  х² + 2х – 48 < 0. 

7.   Чи проходить графік функції y x4 через точки А(0;2), В(8;2), С(16;12)?

ІІІ частина ( за завдання 3 бали)

8.   Побудуйте графік функції f(х). За графіком визначити область значень функції, проміжки знакосталості, зростання і спадання. 

f(х) = х² − х − 6.

Контрольна робота №3

Квадратична функція та її графік

Варіант ІІ І частина ( за кожне завдання 1 бал)

1.     Яка з функцій є квадратичною?

А) у = √х + 8; Б) у = 8х ;    

В) у = х + 8;   Г) у = х² + 8х.

2.     Знайдіть координати вершини параболи у = х² + 4х − 12.

А)  (2;16);   Б)  (-2;-16);   В)  (-2;16);   Г)  (2;-16).

3.     Знайдіть значення функції  fв точці х₀ = -16.

А) 7;    Б) 1;   В)  -1;    Г) 5.

4.     При якому значенні х невизначена функція у = ^х+3  ? 

А) 3;      Б) -8;      В) 8;      Г) -3.

5.     Знайдіть нулі функції у = - 2х∙(х+3).

А)  0; 3;   Б) 0; -3;   В)  ;   Г)   .

ІІ частина (за завдання – 2 бали)

6.     Розв’яжіть нерівність  – х² + 6х – 5 > 0.

7.     Чи проходить графік функції y x3 через точки А(1;2), В(0;3), С(9;6)?

ІІІ частина ( за завдання 3 бали)

8.     Побудуйте графік функції f(х). За графіком визначити область значень функції, проміжки знакосталості, зростання і спадання.

f(х) = −х² − 2х + 3.

Контрольна робота №4

Рівняння з двома змінними і їх системи

Варіант І

І частина ( 1 бал за завдання).

х + у = 1,

1.   Яка пара чисел є розв’язком системи рівнянь.{х₂ − у2 = 9

А) (-3;4);   Б) (5;-4);   В) (4;3);   Г) (-5;4).

у = з,

2.   Розв’яжи систему рівнянь {у + 6 = х₂

А) (-3;3);   Б) (-3;3), (3;3);   В) (3;3);   Г) (3;3), (0;3).

3.   Сума двох чисел 44, а їх різниця 20. Знайдіть ці числа. А) 32 і 76;   Б) 32 і 12;   В) 32 і 52;   Г) 64 і 104.

4.   Знайдіть координати точок перетину графіків рівнянь х+ у=5 і х-у=3. А) (4;1);   Б) (1;4);   В) (3;2);   Г) (2;3).

5.   Сума двох чисел 70. Перше число на 15 більше, ніж друге. Складіть систему рівнянь для розв’язування задачі.

,,

А) ;   Б) ) ;  

,,

 В)  ;   Г)  

ІІ частина(2 бали).

у = х²

6.   Розв’яжи графічно систему рівнянь {     .

у = х + 1

3х + у = 4,

7.   Розв’яжіть систему рівнянь {х₂ − у = 14.

ІІІ частина(4 бали).

8.   Двоє робітників, працюючи разом, закінчили роботу за два дні. За скільки днів виконає цю роботу кожний із них, працюючи окремо, коли відомо, що якби перший попрацював 2 дні, а другий – 1 день, то разом вони б виконали  всієї роботи?

Контрольна робота №4

Рівняння з двома змінними і їх системи

Варіант ІІ І частина( 1 бал за завдання)

1 Яка пара чисел є розв’язком системи рівнянь.

А) (10;-9);   Б) (11;10);   В) (10;9);   Г) (9;10).

у = х²

2.   Розв’яжи систему рівнянь {

у = 9

А) (3;9);   Б) (-3;9);   В) (9;9);   Г) (3;9), (-3;9).

3.   Сума двох чисел 86, а їх різниця 18. Знайдіть ці числа. А) 52 і 138;   Б) 9 і 77;   В) -34 і 52;   Г) 52 і 34.

4.   Знайдіть координати точок перетину графіків рівнянь х+ у=8 і х-у=6. А) (8;2);   Б) (1;7);   В) (7;1);   Г) (4;4).

5.   Сума двох чисел 10, а їх різниця 2. Складіть систему рівнянь для розв’язування задачі.

,,

А) ;   Б) ) ;   

,,

В)  ;   Г)  

ІІ частина( 2 бали).

6.   Розв’яжи графічно систему рівнянь .

7.   Розв’яжіть систему рівнянь .

ІІІ частина( 4 бали).

8.   Дві бригади, працюючи разом, обробили ділянку землі за 12 годин. За який час могла б обробити цю ділянку кожна бригада окремо, якщо їх швидкості виконання робіт відносяться як 3:2 ?