Завдання І туру шкільної олімпіади з математики 2019-2020
Завдання
для шкільного етапу олімпіади з математики
(6 клас)
- У бочці міститься 18 л бензину. Є два відра місткістю по
7 літрів, у які потрібно налити по 6 л бензину. Крім того є черпак місткістю 4 л. Як здійснити розлив?
- У неправильній рівності 2∙3∙2+3∙4∙3=3∙2∙3+4∙3∙2 розставте дужки так, щоб вона стала правильною.
- Відновити ребус ВОДА +ВОДА = ЗАВОД (однаковим літерам відповідають однакові цифри, різним літерам - різні цифри).
- У кожному з чотирьох кутків кімнати сидить кіт. Навпроти кожного кота сидить три коти. Скільки котів у кімнаті?
- Повна діжечка квасу має вагу 34 кг, а наповнена на половину має вагу 17,75 кг. Яка вага порожньої діжки?
 Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості.
Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості.
Завдання
для шкільного етапу олімпіади з математики
(6 клас)
- У бочці міститься 18 л бензину. Є два відра місткістю по
7 літрів, у які потрібно налити по 6 л бензину. Крім того є черпак місткістю 4 л. Як здійснити розлив?
- У неправильній рівності 2∙3∙2+3∙4∙3=3∙2∙3+4∙3∙2 розставте дужки так, щоб вона стала правильною.
- Відновити ребус ВОДА +ВОДА = ЗАВОД (однаковим літерам відповідають однакові цифри, різним літерам - різні цифри).
- У кожному з чотирьох кутків кімнати сидить кіт. Навпроти кожного кота сидить три коти. Скільки котів у кімнаті?
- Повна діжечка квасу має вагу 34 кг, а наповнена на половину має вагу 17,75 кг. Яка вага порожньої діжки?
 Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості.
Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості.
Завдання
для шкільного етапу олімпіади з математики
(8 клас)
- Дано числа: 1, 2, 3, 4, 5, 6, 7, 8, 9. Розташуйте їх по чотири на кожній стороні трикутника так, щоб суми на кожній стороні трикутника були рівними: а) одному парному числу; б) одному непарному числу; в) трьом послідовним натуральним числам.
- На конверт потрібно наклеїти марки по 4 коп. і 9 коп. Загальна вартість конвертів становить 35 коп. Скільки потрібно взяти марок по 4 коп.?
- В сім’ї четверо дітей, їм 5, 8, 13, 15 років. Дітей звуть Марійка, Борис, Віра і Галя. Скільки років кожній дитині, якщо одна дівчинка ходить у дитячий садок, Марійка старша Бориса, а сума років Марійки і Віри ділиться на 3?
- Розв’яжіть рівняння.
а) |x+5|=7; б) |x-3|=0; в) |x+3|=-2;
г) |3x-5|=8; д) |5-4x|=-3; е) |4-3x|=1;
- У 8-А класі навчається 30 учнів. Тільки двоє з них нудьгують на уроках математики, фізики, і біології. 14 учнів люблять розв’язувати задачі з математики, 15 учням подобається проводити досліди з фізики, 11 учнів заслуховуються на уроках біології, 6 із задоволенням відвідують уроки фізики і математики, 5 – фізики і біології та 3 – математики і біології. Скільки учнів полюбляють відразу 3 згадані предмети?
 Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості
Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості
Завдання
для шкільного етапу олімпіади з математики
(8 клас)
- Дано числа: 1, 2, 3, 4, 5, 6, 7, 8, 9. Розташуйте їх по чотири на кожній стороні трикутника так, щоб суми на кожній стороні трикутника були рівними: а) одному парному числу; б) одному непарному числу; в) трьом послідовним натуральним числам.
- На конверт потрібно наклеїти марки по 4 коп. і 9 коп. Загальна вартість конвертів становить 35 коп. Скільки потрібно взяти марок по 4 коп.?
- В сім’ї четверо дітей, їм 5, 8, 13, 15 років. Дітей звуть Марійка, Борис, Віра і Галя. Скільки років кожній дитині, якщо одна дівчинка ходить у дитячий садок, Марійка старша Бориса, а сума років Марійки і Віри ділиться на 3?
- Розв’яжіть рівняння.
а) |x+5|=7; б) |x-3|=0; в) |x+3|=-2;
г) |3x-5|=8; д) |5-4x|=-3; е) |4-3x|=1;
- У 8-А класі навчається 30 учнів. Тільки двоє з них нудьгують на уроках математики, фізики, і біології. 14 учнів люблять розв’язувати задачі з математики, 15 учням подобається проводити досліди з фізики, 11 учнів заслуховуються на уроках біології, 6 із задоволенням відвідують уроки фізики і математики, 5 – фізики і біології та 3 – математики і біології. Скільки учнів полюбляють відразу 3 згадані предмети?
 Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості
Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості
Завдання
для шкільного етапу олімпіади з математики
(9 клас)
- Пляшка, що може вмістити 1/3 літра, заповнена на 3/4 водою. Скільки води залишиться в пляшці після того, як з неї вилити 200мл?
А: нічого не залишиться; Б: 50мл; В: 75мл;
Г: 130мл; Д: 245мл.
- Три вівторки у місяці припадають на парні числа. Який день тижня припадає на 21–е число цього місяця? А: середа; Б:четвер; В: п’ятниця; Г: субота; Д: неділя.
- Ванда розрізає квадратний лист паперу з периметром 20см на два прямокутники. Периметр одного з них дорівнює 16см. Яким є периметр другого прямокутника? А: 8см; Б: 9см; В: 12см; Г: 14см; Д: 16см.
- У магазині два іграшкових кенгуру мали однакову ціну. Перша іграшка подешевшала на 5 %, а друга подорожчала на 15%. Після цього різниця в ціні іграшок стала 6 грн. Якою стала ціна дешевшої іграшки кенгуру?
А: 1 грн.50 коп. Б: 6 грн. В: 28 грн.50 коп.
Г: 30 грн. Д: 34 грн.50 коп.
-
Числа α і
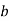 мають різні знаки. Який з виразів, запропонованих у відповідях, є найбільшим? А. (
мають різні знаки. Який з виразів, запропонованих у відповідях, є найбільшим? А. (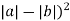 Б.
Б. 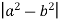 В. (α +
В. (α +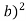
Г. (α ![]() Д.
Д. ![]()
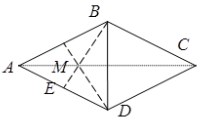
- Дві висоти ромба, проведені з вершин його тупих кутів, перетинаються та діляться у відношенні 1:2. Знайти кути ромба.
Завдання
для шкільного етапу олімпіади з математики
(9 клас)
- Пляшка, що може вмістити 1/3 літра, заповнена на 3/4 водою. Скільки води залишиться в пляшці після того, як з неї вилити 200мл?
А: нічого не залишиться; Б: 50мл; В: 75мл;
Г: 130мл; Д: 245мл.
- Три вівторки у місяці припадають на парні числа. Який день тижня припадає на 21–е число цього місяця? А: середа; Б:четвер; В: п’ятниця; Г: субота; Д: неділя.
- Ванда розрізає квадратний лист паперу з периметром 20см на два прямокутники. Периметр одного з них дорівнює 16см. Яким є периметр другого прямокутника? А: 8см; Б: 9см; В: 12см; Г: 14см; Д: 16см.
- У магазині два іграшкових кенгуру мали однакову ціну. Перша іграшка подешевшала на 5 %, а друга подорожчала на 15%. Після цього різниця в ціні іграшок стала 6 грн. Якою стала ціна дешевшої іграшки кенгуру?
А: 1 грн.50 коп. Б: 6 грн. В: 28 грн.50 коп.
Г: 30 грн. Д: 34 грн.50 коп.
-
Числа α і
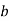 мають різні знаки. Який з виразів, запропонованих у відповідях, є найбільшим? А. (
мають різні знаки. Який з виразів, запропонованих у відповідях, є найбільшим? А. (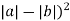 Б.
Б. 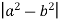 В. (α +
В. (α +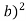
Г. (α ![]() Д.
Д. ![]()
- Дві висоти ромба, проведені з вершин його тупих кутів, перетинаються та діляться у відношенні 1:2. Знайти кути ромба.

7. В сім’ї четверо дітей, їм 5, 8, 13, 15 років. Дітей звуть Марійка, Борис, Віра і Галя. Скільки років кожній дитині, якщо одна дівчинка ходить у дитячий садок, Марійка старша Бориса, а сума років Марійки і Віри ділиться на 3?
І частина містить 5 завдань у тестовій формі. За кожне виконане завдання нараховується 0-2 бали. Загальна кількість балів – 10.
ІІ частина містить 2 завдання з відкритою відповіддю. За кожне виконане завдання нараховується 0-7 балів. Загальна кількість балів – 14. Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості

7. В сім’ї четверо дітей, їм 5, 8, 13, 15 років. Дітей звуть Марійка, Борис, Віра і Галя. Скільки років кожній дитині, якщо одна дівчинка ходить у дитячий садок, Марійка старша Бориса, а сума років Марійки і Віри ділиться на 3?
І частина містить 5 завдань у тестовій формі. За кожне виконане завдання нараховується 0-2 бали. Загальна кількість балів – 10.
ІІ частина містить 2 завдання з відкритою відповіддю. За кожне виконане завдання нараховується 0-7 балів. Загальна кількість балів – 14. Повне розв’язання - 7 балів. Правильна відповідь - 1 бал. Часткові просування або помилки оцінюються в залежності від їх величини та значущості



про публікацію авторської розробки
Додати розробку
