Завдання+відповіді до ДПА з математики, 9 клас
- Бланки відповідей.doc doc
- Варіанти 1-10.docx docx
- Критерии оценивания.docx docx
- Правильні відповіді.docx docx
РОБОТА
на державну підсумкову атестацію
з математики
за курс основної школи
учня/учениці 9_____класу
назва навчального закладу
прізвище, ім’я, по-батькові учня (учениці) в родовому відмінку
Варіант №_____
УВАГА! Позначайте до кожного завдання тільки один варіант відповіді. Будь-які виправлення в бланку недопустимі.
Якщо ви вирішили змінити відповідь у деяких завданнях, то правильну відповідь можна зазначити в спеціально відведеному місці, розташованому внизу бланка відповідей
У завданнях 1.1-1.12 правильну відповідь позначайте тільки так:
![]()
![]()
![]()
|
|
А |
Б |
В |
Г |
|
А |
Б |
В |
Г |
|
А |
Б |
В |
Г |
|
1.1 |
|
|
|
|
1.5 |
|
|
|
|
1.9 |
|
|
|
|
|
1.2 |
|
|
|
|
1.6 |
|
|
|
|
1.10 |
|
|
|
|
|
1.3 |
|
|
|
|
1.7 |
|
|
|
|
1.11 |
|
|
|
|
|
1.4 |
|
|
|
|
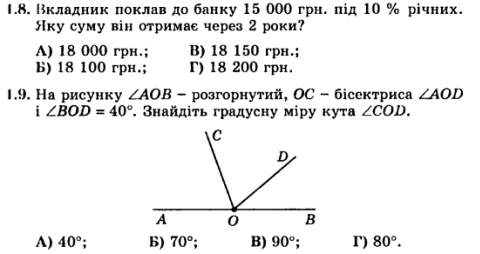
1.8 |
|
|
|
|
1.12 |
|
|
|
|
У завданнях 2.1-2.4 впишіть відповідь.
|
2.1 |
|
2.3 |
|
|
2.2 |
|
2.4 |
|
Щоб виправити відповідь до завдання, запишіть його номер у спеціально відведеній клітинці, а правильну на Вашу думку, відповідь – у відповідному місці.
Завдання 1.1 – 1.12
|
|
|
А |
Б |
В |
Г |
|
1. |
|
|
|
|
|
|
1. |
|
|
|
|
|
|
1. |
|
|
|
|
|
|
1. |
|
|
|
|
|
Завдання 2.1-2.4
|
Номер завдання |
Виправлена відповідь |
|
2. |
|
|
2. |
|
|
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
1.11 |
1.12 |
2.1 |
2.2 |
2.3 |
2.4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3.1 |
3.2 |
3.3 |
||||||||||||||||
|
|
|
|
||||||||||||||||
Загальна кількість балів Оцінка
Голова атестаційної комісії
Члени комісії
ВАРІАНТ 1
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.

Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Знайти чотири послідовні непарі натуральні числа, якщо добуток другого і третього числа на 111 більше, ніж потроєна сума першого і четвертого чисел.
3.2. Розв’яжіть систему рівнянь 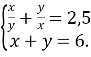
3.3. Доведіть, що чотирикутник АВСD з вершинами в точках А(3; –1),
В(2; 3), С(–2; 2), D(–1;–2) є прямокутником.
ВАРІАНТ 2
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.

Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Власна швидкість човна 18 км/год. Відстань 20 км за течією річки човен подолав на 15 хв швидше, ніж проти течії. Знайти швидкість течії річки.
3.2. Знайти значення виразу 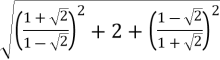 .
.
3.3. Основи прямокутної трапеції дорівнюють 9 см і 5 см, а діагональ поділяє її гострий кут навпіл. Знайти площу трапеції.
ВАРІАНТ 3
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
![]()
![]()
![]()
![]()

2.4. В прямокутній трапеції гострий кут дорівнює 450. Менша бічна сторона і менша основа трапеції – по 6 см. Знайти середню лінію трапеції.
Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Катер проплив 40 км за течією річки і 16 км проти течії, витративши на весь шлях 3 год. Яка власна швидкість катера, якщо швидкість течії 2 км/год?
3.2. Відомо, що для довільного натурального n сума Sn членів деякої арифметичної прогресії обчислюється за формулою ![]() Знайти перший член прогресії та її різницю.
Знайти перший член прогресії та її різницю.
3.3. В прямокутну трапецію вписано коло. Точка дотику ділить більшу бічну сторону на відрізки 8 см і 18 см. Знайти периметр трапеції.
ВАРІАНТ 4
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
![]()
![]()
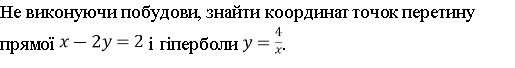
![]()

Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Човен за 5 год руху за течією і 2 год руху озером долає 123 км. За 5 год за течією човен долає відстань у 3 рази більшу, ніж за 2 год проти течії. Знайти власну швидкість човна і швидкість течії.
3.2. Доведіть, що при всіх дійсних значеннях а виконується нерівність:
![]()
3.3. Гострий кут паралелограма дорівнює 600, а діагональ ділить тупий кут у відношенні 3 : 1. Знайти периметр паралелограма, якщо його менша діагональ дорівнює 43 см.
ВАРІАНТ 5
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
![]()
![]()
![]()
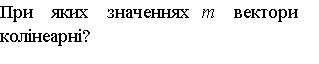

Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Турист проплив на моторному човні проти течії річки 18 км, а повертався назад на плоту. На човні турист плив на 4,5 год менше, ніж на плоту. Знайти швидкість течії, якщо власна швидкість човна 15 км/год.
3.2.Розв’яжіть систему рівнянь ![]()
3.3. Основи трапеції дорівнюють 2 см і 18 см, а діагоналі – 15 см і 7 см. Знайти площу трапеції.
ВАРІАНТ 6
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.

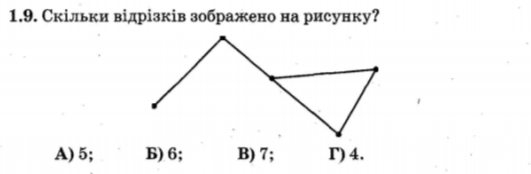
1.9. В якій точці знаходиться центр кола, вписаного в даний трикутник?
А) В точці перетину бісектрис трикутника;
Б) В точці перетину висот трикутника;
В) В точці перетину серединних перпендикулярів до сторін трикутника;
Г) В точці перетину медіан трикутника.

Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
![]()
![]()
![]()

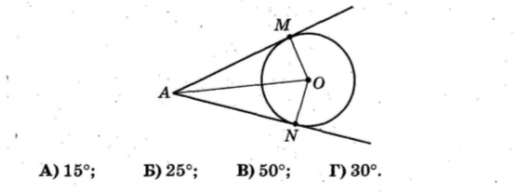
2.4. В рівнобічній трапеції діагональ дорівнює більшій основі і утворює з нею кут 500. Знайти градусну міру тупого кута трапеції.
Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Різниця половини першого числа і третини другого числа дорівнює 2. Якщо перше число зменшити на його четверту частину, а друге число збільшити на його шосту частину, то сума отриманих чисел буде дорівнювати 53. Знайти ці числа.
![]()
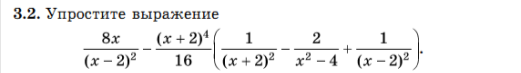
3.3. Кути паралелограма відносяться як 2:3. Знайти кут між висотами паралелограма, проведеними з вершини гострого кута.
ВАРІАНТ 7
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.

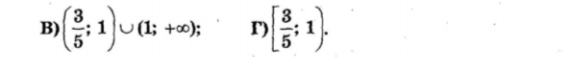


Частина друга
Розв’яжіть завдання 2.1-2.4. Запишіть відповідь у бланк відповідей.
![]()
![]()
![]()

2.4. Дано вектори ![]() Знайти кут між векторами
Знайти кут між векторами ![]() і
і ![]() .
.
Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Потяг мав проїхати 300 км. Проїхавши ![]() шляху, він зупинився на 1 год, а потім продовжив рух зі швидкістю на 10 км/год меншу від початкової. Знайти швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду.
шляху, він зупинився на 1 год, а потім продовжив рух зі швидкістю на 10 км/год меншу від початкової. Знайти швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду.
3.2. Знайти всі цілі числа, які є розв’язками системи нерівностей
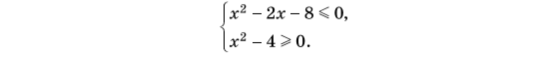
3.3. Висота ромба, проведена з вершини тупого кута, поділяє сторону навпіл. Знайти площу ромба, якщо його більша діагональ дорівнює ![]() см.
см.
ВАРІАНТ 8
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.



Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Два автомобілі одночасно виїхали з одного міста в інше. Швидкість першого на 10 км/год більша за швидкість другого, тому він був на 1 год менше в дорозі. Знайти швидкість кожного автомобіля, якщо відстань між містами 560 км.
3.2. Знайти область допустимих значень функції
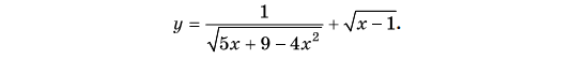
3.3. Медіани прямокутного трикутника, проведені до катетів, дорівнюють 3 см і 4 см. Знайти гіпотенузу трикутника.
ВАРІАНТ 9
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.




Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. Знайти чотири послідовні непарі натуральні числа, якщо добуток другого і третього числа на 111 більше, ніж потроєна сума першого і четвертого чисел.
3.2.Розв’яжіть систему рівнянь 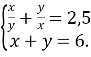
3.3. Доведіть, що чотирикутник АВСD з вершинами в точках А(3; –1), В(2; 3),
С(–2; 2), D(–1;–2) є прямокутником.
ВАРІАНТ 10
Частина перша
Завдання 1.1.–1.12. мають чотири варіанти відповіді, серед яких лише ОДНА ПРАВИЛЬНА. Оберіть правильну відповідь і позначте її у бланку відповідей.




Частина третя
Розв’язання задач 3.1-3.3.повинно мати обґрунтування. У ньому необхідно записати послідовні логічні дії і пояснення, зробити посилання на математичні факти, з яких випливає те чи інше твердження. Якщо потрібно, проілюструйте розв’язання схемами, графіками, таблицями.
3.1. О 9:00 від пристані відчалив плот, а о 18:00 – човен, який наздогнав плот на відстані 20 км від пристані. О котрій годині човен наздогнав плот, якщо власна швидкість човна 18 км/год?
3.2.Розв’яжіть систему нерівностей 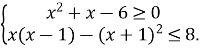
3.3. В трикутнику одна сторона дорівнює 29 см, а інша ділиться точкою дотику вписаного кола на відрізки 24 см і 1 см, рахуючи від кінця першої сторони. Знайти площу трикутника.
Пояснительная записка
Каждый вариант аттестационной работы состоит из трех частей, которые отличаются по сложности и форме тестовых заданий.
В первой части аттестационной работы предложено 12 заданий с выбором одного правильного ответа (8 заданий по алгебре и 4 задания по геометрии). Для каждого тестового задания с выбором ответа дано четыре варианта ответа, из которых только один является правильным. Задание с выбором ответа считается выполненным правильно, если в бланке ответов указана только одна буква, которой обозначен правильный ответ (образец бланка и правила его заполнения приведены в конце книги). При этом учащийся не должен приводить какие-либо соображения, поясняющие его выбор.
Правильное решение каждого задания этого блока №№ 1.1–1.12
оценивается одним баллом.
Вторая часть аттестационной работы состоит из 4 заданий (3 задания по алгебре и 1 задание по геометрии) открытой формы с коротким ответом. Такое задание считается выполненным правильно, если в бланке ответов записан правильный ответ (например, число, выражение, корни уравнения и т. п.). Все необходимые вычисления, преобразования и т. д. учащиеся выполняют на черновиках.
Правильное решение каждого из заданий №№ 2.1–2.4 этого блока оценивается двумя баллами.
Третья часть аттестационной работы состоит из 3 заданий (2 задания по алгебре и 1 задание по геометрии) открытой формы с развернутым ответом. Задания третьей части считаются выполненными правильно, если учащийся привел развернутую запись решения задания с обоснованием каждого этапа и дал правильный ответ. Правильность выполнения заданий третьей части оценивает учитель согласно критериям и схеме оценивания заданий.
Правильное решение задания №3.1 оценивается четырьмя баллами, а заданий №№ 3.2-3.3. – по 6 баллов.
Задания третьей части аттестационной работы учащиеся выполняют на листах со штампом соответствующего общеобразовательного учебного заведения.
Государственная итоговая аттестация по математике проводится в течение 135 мин для учащихся общеобразовательных классов.
Сумма баллов, начисленных за правильно выполненные учащимся задания, переводится в оценку по 12-балльной системе оценивания учебных достижений учащихся по специальной шкале.
Система начисления баллов за правильно выполненное задание для оценивания работ учащихся общеобразовательных классов приведена в таблице 1.
Таблица 1.
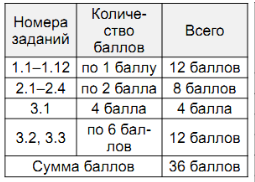
Соответствие количества баллов, набранных учащимся общеобразовательного класса, оценке по 12-балльной системе оценивания учебных достижений учащихся приведено в таблице 2.
Таблица 2.
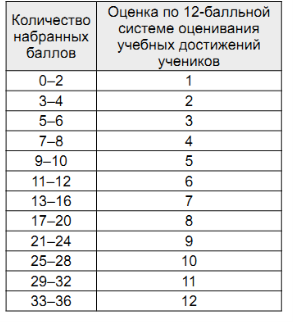
Если в бланке ответов указан правильный ответ к заданию первой или второй части, то за это начисляется 1 или 2 балла в соответствии с таблицей 1. Если указанный ответ является неправильным, то баллы за такое задание не начисляются. В некоторых случаях за частичное выполнение задания второй части начисляется 1 балл (например, если найдено правильно одно из двух решений системы уравнений, одна из мер центральной тенденции выборки и т. п.).
Если учащийся считает необходимым внести изменения в ответ к какому-то из заданий первой или второй части, то он должен сделать это в специально отведенной для этого части бланка. Такое исправление не ведет к потере баллов. Если же исправление сделано в основной части бланка ответов, то баллы за такое задание не начисляются.
Формулировки заданий третьей части учащиеся не переписывают, а указывают только номер задания. Исправления и зачеркивания в оформлении решений заданий третьей части, если они сделаны аккуратно, не являются основанием для снижения оценки.
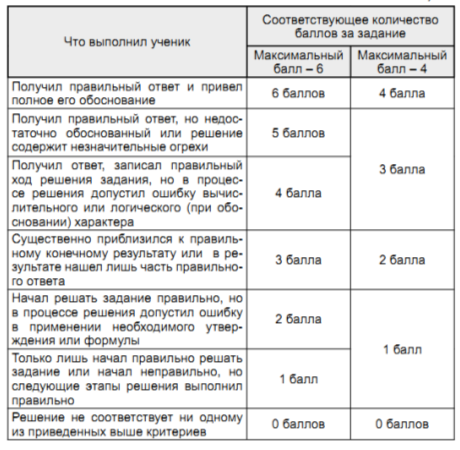
Критерии оценивания заданий из третьей части приведены в таблице 3.
Таблица 3.
|
Варіант
№ зав-дання |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1.1 |
В |
Б |
А |
Б |
Б |
Г |
Б |
В |
В |
Г |
|
1.2 |
А |
Г |
Б |
Г |
Г |
В |
Г |
Г |
В |
Б |
|
1.3 |
Б |
В |
Г |
В |
В |
Б |
В |
А |
А |
В |
|
1.4 |
Г |
Б |
Б |
А |
А |
А |
Б |
В |
Б |
В |
|
1.5 |
А |
А |
В |
Б |
Б |
В |
Г |
В |
Б |
Г |
|
1.6 |
В |
Г |
Г |
Г |
В |
Г |
А |
В |
Б |
А |
|
1.7 |
Б |
Б |
Б |
Г |
Б |
В |
В |
Г |
В |
В |
|
1.8 |
Б |
В |
В |
А |
Г |
Б |
Б |
В |
Г |
Б |
|
1.9 |
Б |
А |
Г |
В |
В |
А |
А |
Б |
Б |
Б |
|
1.10 |
А |
Б |
Г |
Г |
А |
Б |
Б |
Б |
А |
Б |
|
1.11 |
Г |
В |
В |
Г |
Б |
Г |
В |
А |
Г |
А |
|
1.12 |
В |
Г |
Г |
В |
А |
Б |
Б |
А |
Г |
Б |
|
|
||||||||||
|
2.1 |
9 |
|
|
|
|
|
|
|
-1 |
4 |
|
2.2 |
(0;2) |
1000 |
|
|
-2 |
|
1; 2 |
-7; -6 |
0; 1 |
-1 |
|
2.3 |
5; 2 |
29 |
|
(4;1), (-2;-2) |
|
9 |
|
2; -5 |
3; -2 |
-1 |
|
2.4 |
7 |
24 |
9 |
16 |
|
115 |
45 |
60 |
9 |
6 |
-
Дякую, але критерії оцінювання повинні бути теж українською мовою.

про публікацію авторської розробки
Додати розробку
