Завдання з логічним навнтаженням "Інтелектуальні завдання з математики для роботи з обдарованими учнями"
Завдання з математики вміщують арифметичні ребуси, задачі на логічне мислення. Їх можна використовувати на уроках при роботі з обдарованими дітьми. Ці завдання стануть у нагоді при підготовці до математичних конкурсів для індивідуальних завдань.
Відділ освіти Чугуївської міської ради Харківської області
ІНТЕЛЕКТУАЛЬНІ
ЗАВДАННЯ З МАТЕМАТИКИ
ДЛЯ РОБОТИ
З ОБДАРОВАНИМИ УЧНЯМИ
(4 клас )
ЧУГУЇВ
2018 р.
Цей збірник об'єднує матеріали учасників творчої групи, в якому знаходяться розроблені та упорядковані завдання з математики для роботи з обдарованими учнями, для підготовки їх до олімпіад, математичних конкурсів, для розвитку інтелектуальних здібностей.
Автори -упорядники:
Бочева Людмила Вікторівна, учитель початкових класів, спеціаліст вищої категорії, учитель-методист, Чугуївський НВК «ЗОШ І -ІІІ ступенів - гімназія №5 Чугуївської міської ради Харківської області»;
Копніна Людмила Юріївна, учитель початкових класів, спеціаліст вищої категорії, Чугуївська ЗОШ І – ІІІ ступенів № 4 Чугуївської міської ради Харківської області»;
Римар Світлана Анатоліївна, учитель початкових класів, спеціаліст вищої категорії, учитель-методист, Чугуївська ЗОШ І – ІІІ ступенів № 4 Чугуївської міської ради Харківської області»;
Інтелектуальні завдання
з математики для 4 класу
Вступ
Ми пропонуємо матеріал для роботи на уроці, вдома. В залежності від рівня підготовки класу учитель сам визначає, яку задачу вибрати. Матеріал систематизований за темами, до них подані рекомендації, відповідь або розв’язання. Ці завдання можна використовувати для роботи вдома з батьками.
Однією з характеристик, що відрізняє обдаровану людину є любов до пізнання нового. У таких дітей висока пошукова активність. Обдаровані діти отримують задоволення від розумового навантаження, вони не бояться складних, заплутаних завдань, задач з декількома правильними відповідями. Бажання використовувати для пошуку правильної відповіді неоднозначність, неординарні прийоми – це одна з головних рис обдарованої дитини.
Виявлення та розвиток обдарованих та здібних дітей є однією із актуальних проблем сучасної освіти, яка має забезпечувати розвиток творчих здібностей, формування навичок самостійного наукового пізнання, самоосвіти і самореалізації кожної дитини. Формами розвитку здібностей і обдарувань молодших школярів є участь учнів 2-4 класів у конкурсах та олімпіадах.
Математична олімпіада – це змагання школярів в галузі математики для виявлення рівня знань і вмінь та підвищення рівня підготовки учасників.
Як готуватися до таких змагань? Чи потрібно готуватися до таких змагань? Підготовка до математичної олімпіади починається з роботи на уроці. Практично на кожному уроці потрібно розв’язувати логічні задачі, завдання на кмітливість, арифметичні ребуси.
Мета олімпіад – виявлення обдарованих, талановитих учнів, удосконалення їх підготовки.
Підготовка учнів до участі в математичній олімпіаді здійснюється на уроках, шляхом проведення індивідуальної і групової роботи, упровадження диференціації класних і домашніх завдань, а також у позаурочній, позакласній творчо-пошуковій діяльності молодших школярів, у ході проведення класних олімпіад та ін..
Математична олімпіада стимулює учнів до самоосвіти, викликає поглиблений інтерес до математики, виробляє навички самостійної роботи, наполегливість, уміння долати труднощі. На математичних олімпіадах пропонуються задачі, які мають виявити рівень математичної підготовленості учнів, їхнє вміння логічно мислити, аналізувати, порівнювати, зіставляти, узагальнювати. Олімпіади в молодших класах мають пропедевтичний характер.
Не кожна дитина має змогу одержати допомогу в підготовці до олімпіади з боку старших членів родини. Таку допомогу слід очікувати від учителя, його плідної роботи на уроках та систематичної участі в позакласній роботі. Учитель має планомірно готувати учнів до участі в олімпіаді: розв’язувати з ними олімпіадні задачі, розповідати про порядок проведення олімпіади, про поведінку на олімпіаді, здійснювати відповідну психологічну підготовку майбутніх учасників олімпіади, щоб запобігти стресовим ситуаціям.
МАТЕМАТИЧНІ РЕБУСИ.
1. Як можна записати 8 5-ма п’ятірками?
5+(5+5+5):5=8
2. Як можна записати 7 5-ма двійками?
(2 * 2 * 2 – ( 2:2 ) = 7
3. Як можна записати 21 4-ма двійками?
(22 – 2 : 2) =21
4. Як можна записати 27 6-ма чотвірками? 5 – ма п’ятірками?
А). (4 + 4 ) * 4 – ( 4 + 4 : 4 ) =27
Б). 5 * 5 + ( 5 + 5 ) : 5 = 27
5. Коли цифра «2» означає «10»?
Відповідь. На циферблаті цифра «2» відповідає «10 хвилин».
6. Розшифруй приклад на додавання, якщо В = 0
А Б
+ А
Б В В
Відповідь. А = 9, Б = 1
7. Запишіть число 100 п’ятьма трійками.
Розв’язання
33∙3+3:3=100
8. Постав знаки дій між цифрами так, щоб рівність стала правильною.
А) 3 3 3 3 = 30
Б) 3 3 3 3 3 = 30
В) 3 3 3 3 3 3 = 30
Розв’язання.
А) 3 х 3 х 3 + 3 = 30
Б) 33 – 3 + 3 – 3 = 30
9. Кожну букву заміни цифрою так, щоб вийшла правильна арифметична рівність. Однаковим буквам відповідають однакові цифри, різним буквам – різні цифри. Відомо, що буква Ю означає цифру 6.
Т Р Ю К
+ Т Р Ю К
Ц И Р К
Розв’язання.
В ребусі буква Ю за умовою означає цифру 6. Букву К можна замінити тільки на цифру 0, бо сума двух однакових цифр закінчується на ту ж цифру. Буква Р означає цифру 2, буква И означає цифру 5. Буква Т може бути замінена на цифру 4, і тоді буква Ц означає цифру 8.
4 2 6 0
+ 4 2 6 0
________
8 5 2 0
10. Якщо найбільше трицифрове число зменшити на найбільше двоцифрове число, отримане поділити на 4, потім відняти 25, то вийде вік мудреця. Скільки років мудрецю?
Розв’язання.
- – 99) : 4 – 25 = 200 (років)
11. Розставити числа 1, 2, 3, 4, 5, 6 у кружечки так, щоб сума чисел уздовж кожної прямої дорівнювала 12.
Розв’язання
12. Скільки серед чисел від 100 до 1000 включно таких, у запису яких зустрічається три однакові цифри?
ВІДПОВІДЬ :10 чисел :111, 222, 333, 444, 555, 666, 777, 888, 999, 1000.
13. Якщо скласти зменшуване, від'ємник і різницю, то вийде 140. Знайдіть зменшуване, від'ємник і різницю, якщо різниця менше зменшуваного на 28.
Розв'язання.
140:2=70 - зменшуване,
70-28=42 - різниця,
28 - від'ємник 3.
14. Шестизначне число закінчується цифрою 4. Якщо цю цифру переставити з кінця числа на початок, тобто приписати її перед першою, не змінюючи порядку решти п'яти, то вийде число, яке в 4 рази більше початкового. Знайдіть це число.
Розв'язання.
102564 *4 = 410256
15. Знайдіть помилку:
(48-34)∙а=48
57∙с+32=89∙с
32∙7+45∙7=32+45∙7
Розв’язання
(48-34)∙а=48
57∙с+32∙с=89∙с
32∙7+45∙7=(32+45)∙7
16. А) Паліндромом є дата 13 лютого 2031 року, бо це можна записати як 13.02.2031.
Створи дату-паліндром для 17 грудня. Це минулий чи майбутній час?
Б) У який день 3002 рік створить дату-паліндром?
Розв’язання
А) 17.12.2171. Майбутній час.
Б) 20. 03.3002
ЗАДАЧІ на знаходження невідомих за сумою і різницею .
ЗАДАЧА 1.
У ставку плавають 32 качки та гуски. Качок на 8 більше ніж гусок. Скільки окремо качок та гусок ?
РОЗВ’ ЯЗАННЯ
Позначимо кількість гусок як 1 частину, а кількість качок - (1 ч. + 8 ).
І спосіб розв’язання:
1)1+1= 2 (ч.)
2)32- 8 =24(шт.)- на 2 ч.,подвійна кількість гусок;
3)24: 2 =12 (шт.)- на 1 ч., кількість гусок;
4) 12 + 8 =20 (шт.)-качок.
ПЕРЕВІРКА: 20 + 12 = 32 (шт.)
ІІ спосіб розв’язання:
- + 1 = 2(ч.)
2) 32 – 8 = 24 (шт.)- на 2ч., подвійна кількість гусок;
3) 24 : 2 = 12 (шт.)- на 1 ч..кількість гусок;
4) 32 – 12 = 20 (шт.)
ІІІ спосіб розв’язання:
Зрівняємо кількості качок і гусок, збільшивши кількість гусок на 8 . тоді їх буде:
1)32+ 8 = 40(шт.) - подвійна кількість качок;
2)40 : 2 = 20 (шт.) – качок;
3)20 – 8 = 12 (шт.) - гусок.
Відповідь : 12 гусок , 20 качок.
ЗАДАЧА 2.
У вазі лежало 24 груші і яблука. Груш було на 6 більше ніж яблук. Скільки окремо груш і яблук лежало у вазі?
РОЗВ’ЯЗАННЯ:
Позначимо кількість яблук як 1 частину, а кількість груш – ( 1ч.+6).
- 1 + 1 = 2 (ч.)
- 24 – 6 = 18 (шт.)- на 2 частини;
- 18 :2 = 9 (шт.)- на 1 частину, кількість яблук;
- 9 + 6 = 15 (шт.) – груш.
ВІДПОВІДЬ: 15 груш, 9 яблук.
ЗАДАЧІ НА ЗНАХОДЖЕННЯ ТРЬОХ НЕВІДОМИХ ЧИСЕЛ ЗА ЇХ СУМОЮ ТА РІЗНИЦЯМИ
ЗАДАЧА 3.
У трьох хлопчиків була 41 цукерка. Коли перший віддав 7 цукерок, другий – 3 цукерки, а третій 4 цукерки , то у кожного залишилась однакова кількість цукерок. Скільки цукерок було у кожного хлопчика спочатку?
РОЗВ’ЯЗАННЯ
Якщо позначити кількості цукерок, що залишились у кожного хлопчика, 1 частиною або рівними відрізками, то спочатку у першого хлопчика була (1 Ч.+ 7) цукерок, у другого –(1ч. + 3 ) цукерки і в третього- (1ч. +4 ) цукерки.
І спосіб
- 7+3+4=14(ц.)- відклали три хлопчики;
- 41 – 14 = 27 (ц.)- припадає на 3 частини;
- 27: 3 = 9 (ц.)- припадає на 1частину;
- 9 + 7 = 16 (ц.)- було у першого хлопчика;
- 9 =3 = 12 (Ц.) – було у другого хлопчика;
- 9 + 4 = 13 (ц.) – було у третього хлопчика.
ПЕРЕВІРКА:
16 + 12 + 13 =41 (ц.)
ВІДПОВІДЬ:16 цукерок, 12 цукерок, 13 цукерок.
ЗАДАЧА 4.
Троє братів спіймали 29 карасів. Коли один брат відклав для юшки 6 штук, другий - 2, третій - 3, то в кожного залишилася рівна кількість карасів. Скільки карасиків спіймав кожен з них?
РОЗВ₴ЯЗАННЯ :
1) 6 + 2 +3 = 11 (К.)- відклали брати;
2) 29 – 11 = 18 (к.)- припадає на 3 частини;
3) 18 : 3 = 6 (к.) – припадає на 1 частину;
4) 6 + 6 = 12( 9к.)- спіймав перший брат;
5 ) 6 + 2 = 8 (к.) – спіймав другий брат ;
6) 6 + 3 = 9(к.) – спіймав третій брат.
ВІДПОВІДЬ: 12 карасів, 8 карасів. 9карасів.
ЗАДАЧІ НА ВИЛУЧЕННЯ
ЗАДАЧА 5.
Для Дар’ї, Софії, Іванка є три пироги: з рисом, капустою і яблуками. Іванко не любить пироги з яблуками і не їсть пироги з капустою. Дар’я не любить пироги з капустою. Хто що їсть?
|
|
РИС |
КАПУСТА |
ЯБЛУКА |
|
Дар’я |
----- |
--- |
+ |
|
Софія |
------ |
+ |
|
|
Іванко |
+ |
--- |
---- |
ВІДПОВІДЬ: Дар’я з яблуками, Софія з капустою, Іванко з рисом.
ЗАДАЧІ НА ВПОРЯДКУВАННЯ
ЗАДАЧА 6.
Іван старший за Петра. Дмитро молодший за Миколу. Петро старший за Миколу. Іван молодший за Юрія . Хто найстарший?
Варіант алгоритму розв’язання.
• Записати умову за допомогою знаків:
І ˃ П, Д˂М,П˃М, І˂Ю.
• Звести всі записи до єдиного вигляду:
І˃П, М˃Д, П˃М, Ю˃І
• Розставити за порядком:
Ю˃І, І˃П, П˃М, М˃Д (або Ю˃І˃П˃М˃Д).
Відповідь на запитання задачі: Юрій найстарший
ЗАДАЧІ НА ПЕРЕТИН МНОЖИН
ЗАДАЧА 7.
У третьому класі навчаються 25 учнів. Їм запропонували відвідати два гуртки: математичний та шаховий. До математичного гуртка записалося 16 учнів, до шахового – 14. Скільки учнів записалися до шахового і математичного гуртків водночас?
РОЗВ’ЯЗАННЯ
(16 + 14 ) – 25 = 5
ВІДПОВІДЬ: 5 учнів .
ЗАДАЧА 8.
На селянському дворі жили гуси й поросята. Господар і його син Іванко вийшли у двір. Іванко питає: «Батьку, скільки у нас гусей і скільки поросят?» Батько відповідає: «Здогадайся сам. Якщо лічити по головах, то у дворі 25 голів, а якщо по ногах , то 70 ніг» Скільки було гусей і скільки поросят?
РОЗВ’ЯЗАННЯ:
- 25 • 2 = 50 (ніг.) – якби всі були гуси;
- 70 – 50 = 20 (ніг)- (у поросят);
- 20 : 2 = 10 (поросят);
- 25 – 10 = 15 (гусей).
ВІДПОВІДЬ: 10 поросят, 15 гусей.
ЗАДАЧА 9.
Маса коробки з зефіром 650 г. Після того, як з’їли половину зефіру, маса коробки - 400г. Якою є маса порожньої коробки?
Розв’язання :
- 650 – 400 = 250 ( г. ) – маса половини зефіру;
- 250•2 = 500 (г.) – маса зефіру;
- 650 – 500 = 150 (г.) – маса коробки.
ВІДПОВІДЬ: 150 грам.
ЗАДАЧА 10.
На 5 тарілках 100 горіхів. На І і ІІ тарілках сумарно 52 горіхи. На ІІ и ІІІ тарілках - 43 горіхи. На ІІІ и ІV - 34 горіхи, на ІV – й та V– 30 горіхів. Скільки горіхів на кожній тарілці?
1). 100 – 52 = 48 (гор.) – на 3, 4 и 5-й тарілках.
2). 48 – 34 = 14 (гор.) – на 5-й тарілці.
3). 30 – 14 = 16 (гор.) – на 4-й тарілці.
4). 34 – 16 = 18 (гор.) – на 3-й тарілці.
5). 43 – 18 = 25 (гор.) – на 2-й тарілці.
6). 52 – 25 = 27 (гор.) – на 1-й тарілці.
Відповідь: 27 горіхів, 25 горіхів, 18 горіхів, 16 горіхів, 14 горіхів.
ЗАДАЧА 11.
Ластівка живе 9 років, що становить 1/3 віку сороки. Ворона живе на 22 роки довше, ніж сорока. Скільки років живе ворона?
ЗАДАЧА 12.
На складі 5 бочок з олією: 25л, 25л, 18л, 16л, 15л. Усю олію продали заводу та їдальні, причому завод узяв олії у 2 рази більше, ніж їдальня. Які бочки дістались заводу, а які – їдальні?
1)25л+25л+16л—завод. 2)18л+15л—їдальня.
ЗАДАЧА 13.
Даша купила 4 книги. Всі книги без першої коштують 240 гривень, без другої - 310 гривень, без третьої - 275 гривень, а без четвертої - 300 гривень. Скільки коштують всі 4 книги разом ?
Спільна вартість - Х
(Х-240) - перша книга
(Х-310) - друга
(Х-275) - третя
(Х-300) - четверта
============
Х = ( Х - 240 ) + ( Х - 310 ) + ( Х - 275 ) + ( Х - 300 )
Х=4х-1125
3х=1125
Х = 375 ( грн. ) спільна вартість книг.
Відповідь: 375 гривень.
ЗАДАЧА 14.
Троє друзів дитинства Сергій, Микола і Олег (інженер, лікар, вчитель) зустрілись в купе поїзда. З розмови з’ясувалося, що:
- Сергій і вчитель сиділи за однією партою;
- Інженер і Олег – любителі шахів;
- Микола з лікарем після закінчення школи жодного разу не бачилися;
- Олег з учителем працюють в одному місті.
Назвати імена інженера, лікаря і вчителя.
Вчитель –Микола.
Лікар - Олег. Інженер – Сергій .
ЗАДАЧА 15.
25 стільців і 10 столів коштують 1100 грн. Скільки коштує кожен стілець і кожен стіл окремо, якщо стілець і стіл разом коштують 80 грн.
1)80 * 10 = 800( грн.) – 10 столів і 10 стільців.
2)1100 – 800 =300 (грн. ) – 15стільців.
3)300 : 15 = 20 (грн.) –стілець.
4)80 – 20 = 60 (грн.)
Відповідь: стілець коштує 20 гривень, стіл – 60 гривень.
ЗАДАЧА 16.
Марійка має 16 карт: 4 сині (С), 4 червоні (Ч), 4 зелені (З) і 4 жовті (Ж). Вона хотіла розкласти їх у квадрат так, щоб у кожному стовпчику і рядку були карти різних кольорів. Якого кольору карта буде на місці «?» ?
Обери правильну відповідь: |
а) синя;
б) червона;
в) зелена;
г) жовта;
д) однозначно визначити неможливо.
ЗАДАЧА 17.
Три дівчинки на запитання, скільки років кожній, відповіли:
– Нам разом 25 років.
– Я старша за Наталку на 1 рік.
– Мені разом з Тетянкою 17 років.
Скільки років кожній дівчинці?
Розв’язання
Т.
Я. 17 25
Н. 1
1) 25-17=8 (р.) – Наталі;
2) 8+1=9 (р.) – мені;
3) 17 – 9=8 (р.) Тетяні.
ЗАДАЧА 18.
Іра і Оля пішли по гриби. Вони знайшли 70 грибів. 
грибів, які знайшла Іра, є лисички, а 
грибів, які знайшла Оля є маслюки. Скільки грибів знайшла Іра?
Розв’язання
Іра: 9, 18, 27, 36, 45, 54, 63.
Оля: 17, 34, 51.
Разом вони зібрали 70 грибів. Отже, Іра зібрала 36 грибів, а Оля – 34.
ЗАДАЧА 19.
Петрик, щоб заснути, намагався рахувати слоненят, які весь час крутилися, бігали і ховалися. За першу хвилину він порахував одне слоненя, за другу – 2, за третю – 4 слоненят. Через 5 хвилин усі слоненята були пораховані. Скільки слоненят нарахував Петрик, якщо кожної наступної хвилини, він нараховував їх удвічі більше, ніж попередньої?
Розв’язання
1+2+4=8+16=31 (слоненя)
ЗАДАЧА 20.
М’ячик Стрибайко вирішив трішки прогулятись і вистрибнув і вистрибнув з вікна будинку, яке було на висоті 12 м над землею. Він двічі підскакував і щоразу на половину тієї висоти, з якої падав. Який шлях пролетів Стрибайко до третього удару об землю?
Розв’язання
12+6+6+3+3=30 (м)
ЗАДАЧА 21.
Лев може з'їсти вівцю за 2 год, вовк – за 3 год, а собака – за 6 год. За який час вони разом з'їли б вівцю?
Міркування:
Лев – за 2 год – 1 вівцю
Лев – за 6 год – 3 вівці
Вовк – за 3 год – 1 вівцю
Вовк – за 6 год – 2 вівці
Собака – за 6 год – 1 вівцю
За ? год всі – 1 вівцю.
Разом за 6 год – 6 овець,
а за 1 год – 1 вівцю.
Відповідь: за 1 годину.
ЗАДАЧА 22.
У Андрія і Бориса разом 11 горіхів. У Андрія і Володі – 12 горіхів, у Борі і Володі – 13 горіхів. Скільки всього горіхів у Андрія, Бориса і Володі разом?
Міркування 1. Позначимо кількість горіхів у Андрія – А, у Бориса – Б, у Володі – В. Тоді умову задачі можна записати трьома рівностями:
А + Б = 11
А + В = 12
Б + В = 13
Склавши рівності (1), (2) і (3), отримуємо:
2А = 2Б + 2В = 11 + 12 + 13 = 36
Звідси, А = Б + В = 32 : 2 = 18 горіхів.
Міркування 2. Із рівності (1) і (2) видно, що у Вови на один горіх більше, ніж у Борі: 12 – 11 = 1 (горіх). Оскільки у Вови і Бориса разом 13 горіхів, то можна дізнатися, скільки у них було б горіхів, якби у Вови було стільки ж горіхів, скільки і у Бориса: 13 – 1 = 12 (горіхів). Тоді у Вови 6 + 1 = 7 (горіхів), а у Андрія 11 – 6 = 5 (горіхів), а у всіх разом 5 + 6 + 7 = 18 (горіхів).
ЗАДАЧА 23.
На запитання, скільки важить рибина, рибалка відповів: «Хвіст важить 150 г, голова стільки, скільки хвіст і половина тулуба, а тулуб – скільки голова і хвіст разом. Скільки важить ціла рибина?
Міркування: Вага голови дорівнює вазі хвоста плюс половина ваги тулуба. Із умови задачі випливає, що вага тулуба дорівнює вазі хвоста плюс половина ваги тулуба, плюс вага хвоста. Значить, половина ваги тулуба дорівнює вазі двох хвостів, тобто 150 · 2 = 300 г, а весь тулуб важить 600 г, і тоді вага голови дорівнює: 150 + 300 + 450 г. Тоді вага риби дорівнює: 450 + 600 + 150 = 1200 г = 1 кг 200г.
ЗАДАЧА 24.
Шість однакових бочок уміщують 28 відер води. Скільки відер води уміщують 15 таких бочок?
Міркування. 15 бочок можна подати як 6 бочок + 6 бочок + 3 бочки. 6 бочок уміщують 28 відер води. Тоді 3 бочки вміщують 14 відер води. Отже, 15 бочок уміщують 70 відер води.
ЗАДАЧА 25 .
У неділю рибалка ловив рибу 3 рази: вранці, вдень і ввечері. Весь улов – 3 кг, причому, вранці він зловив в 3 рази більше, ніж увечері, а вдень стільки ж, скільки і ввечері. Скільки риби зловив рибалка вранці і ввечері?
Міркування: Вилов риби ввечері – одна частина, вранці – три частини, а вдень – одна частина. Отже, весь улов складає 1 + 3 + 1 = 5 частин; 3 кг = 5 частин, тоді на одну частину припадає 3000 : 5 = 600 г (це вечірній улов), 600 · 1800 г (ранішній улов).
ЗАДАЧА 26.
Іра і Олег взяли у бабусі кошик з яблуками і грушами, всього 25 фруктів. По дорозі додому Іра з’їла одне яблуко і три груші, Олег з’їв три яблука і дві груші. Вдома вони з’ясували, що принесли однакову кількість груш і яблук. Скільки груш вони взяли у бабусі?
Розв’язання: 1 + 3 + 3 + 2 = 9 (фр) – кількість фруктів, які з’їли діти;
(25 – 9) : 2 = 8 (гр.) – кількість грушок, які принесли діти;
8 + 2 + 3 = 13 (гр.) – кількість грушок, які діти взяли у бабусі.
ЗАДАЧА 27.
Дракон має 5 голів. Кожного разу, коли йому відрубують одну голову, виростає п’ять нових. Якщо драконові відрубати шість голів одну за одною, то скільки голів матиме дракон?
Розв’язання: Після відрубування однієї голови у дракона стає на 4 голови більше, ніж спочатку. Тому після шести відрубувань у дракона стане 5 + 6 · 4 = 29 голів.
ЗАДАЧА 28.
12 дітей віком 6, 7, 8, 9 і 10 років були на дні народження. Чотирьом з них по 6 років. Дітей віком 8 років було найбільше. Яким є середній вік усіх 12 дітей?
Розв’язання: чотирьом дітям по 6 років, п’ятьом – по 8 років. Також на дні народженні по одній дитині віком 7, 9 та 10 років.
Середній вік дітей на дні народження (4 · 6 + 5 · 8 + 7 + 9 +10) : 12 = 7,5.
ЗАДАЧІ З ЛОГІЧНИМ НАВАНТАЖЕННЯМ
ЗАДАЧА 29.
Декілька приятелів під час зустрічі потиснули один одному руки. Скільки зустрілось приятелів, якщо рукостискань було 10?
Розв’язання:
2 приятелі – 1 раз,
3 приятелі – 2 + 1 = 3
4 приятелі – 3 + 2 + 1 = 6
5 приятелів – 4 + 3 + 2 + 1 = 10
ЗАДАЧА 30.
У двох братів були марки. Коли старший дав молодшому стільки марок, скільки в молодшого було, а молодший дав старшому стільки, скільки в старшого залишилося, то в обох братів стало по 28 марок. Скільки марок було в кожного брата спочатку?
Розв’язання:
|
Молодший |
Старший |
|
28 |
28 |
|
42 |
14 |
|
21 |
35 |
Відповідь: 21 марка у молодшого, 35 марок у старшого.
ЗАДАЧА 31.
Даринка, Мишко, Мирослава і Ганнуся задумали числа 6, 7, 9 і 11.
Яке число задумала кожна дитина, якщо одна з дівчаток задумала парне число? Даринка задумала число більше, ніж задумав Мишко, а сума чисел Даринки і Ганнусі ділиться на 6.
Розв’язання:
|
|
6 |
7 |
9 |
11 |
|
Даринка |
|
|
|
+ |
|
Мишко |
|
|
+ |
|
|
Мирослава |
+ |
|
|
|
|
Ганнуся |
|
+ |
|
|
ЗАДАЧА 32.
За дві груші дають 3 яблука, а за 6 яблук – півтора десятки слив. Скільки слив дадуть за 12 груш?
Розв’язання:
2 гр. = 3 ябл.
4 гр. = 6 ябл.
4 гр. = 15 сл.
- р. = 45 сл.
ЗАДАЧА 33.
Я задумав число, відняв від нього 16, помножив результат на 4, розділив на 7. Від 144 відняв отриману частку. 288 розділив на отриману різницю, додав 195, отримав 198.
Яке число я задумав?
Розв’язання:
100
198 – 195 = 3
288 : 3 = 96
144 – 96 = 48
48 · 7 = 336
336 : 4 = 84
- + 16 = 100
ЗАДАЧА 34.
Листоноша розніс листи у три будинки. У перший будинок – половину всіх листів та ще 1, у другий – половину тих, що залишилися, та ще 2, а у третій – половину решти та ще 3. Після цього у листоноші листів не залишилося. Скільки листів було у листоноші спочатку?
Розв’язання:
((( 0 + 3) · 2 + 2 ) · 2 + 1 ) · 2 = 34
ЗАДАЧА 35.
Вінні-Пух і Пацик пішли з Тигрою на прогулянку. Як відомо, Тигра дуже любить бігати. Тому він відбіг уперед на 20 м, потім повернувся назад на 25 м, пробіг уперед на 15 м і знову повернувся на 10 м. Як далеко від своїх товаришів опинився Тигра?
Розв’язання:
Зупиниться якраз біля них. (Зробити креслення)
- – 25 + 15 – 10 = 0
ЗАДАЧА 36.
Вінні-Пух не міг дочекатися літа і якось вирвав з календаря всі аркуші травня з парними датами. Скільки травневих аркушів залишилось в календарі?
Розв’язання:
16 аркушів.
Травень має 31 день. 15 – парних, 16 – непарних дат.
ЗАДАЧА 37.
Якщо Буратіно купить 4 олівці, то у нього залишиться 25 коп. Якби за ті самі гроші він хотів купити 7 олівців, то йому б не вистачило 2 коп. Скільки грошей має Буратіно?
Розв’язання:
За 3 олівці Буратіно має заплатити 25 + 2 = 27 (коп)
27 : 3 = 9 (коп.) – коштує 1 олівець
- · 4 + 25 = 61 (коп.) – має Буратіно.
ЗАДАЧА 38.
На свій день народження Крістофер Робін запросив 30 гостей і роздавав усім повітряні кульки. Оскільки кульок було 100, то іменинник роздав найближчим друзям по 4 кульки, а решті гостей – по 3. Скільки найближчих друзів прийшло на день народження?
Розв’язання:
3 30 = 90 (к.) – якби усім роздав по 3 кульки
100 – 90 = 10 (к.) – залишилося, щоб додати ще по 1 кульці найближчим друзям. Отже, було 10 найближчих друзів.
ЗАДАЧА 39.
У класі було 33 дитини. 16 з них мають по сестричці, 20 дітей мають по братику. Оля, Олег, Дмитрик і Катруся не мають ані братика, ані сестрички. Скільки дітей у класі мають і братика, і сестричку?
Розв’язання:
33 – 4 = 29 (д.) – не є одинаками
1 спосіб:
20 + 16 = 36 (д.) – мають братика чи сестричку
Тобто 36 – 29 = 7 (д.) пораховані двічі, отже вони мають і братика, і сестричку.
2 спосіб:
29 – 16 = 13 (д.) – мають лише братика
20 – 13 = 7 (д.) – мають і братика, і сестричку.
ЗАДАЧА 40.
Задача на заміщення
Вага однієї груші і однієї сливи 180 г, а вага однієї груши та чотирьох слив - 300 г. Яка вага трьох груш і п’яти слив разом?
Умовно можна записати так:
1 груша + 1 слива = 180 г
1 груша + 4 сливи = 300 г або 1 груша + 1 слива + 3 сливи = 300 г або
180 г + 3 сливи = 300 г
300 - 180 = 120 г важать 3 сливи
120 : 3 = 40 г важить 1 слива
180 - 40 = 140 г важить 1 груша
3·140 + 5·40 = 420 + 200 = 620 г важать 3 груші і 5 слив разом.
Відповідь: 620 г
ЗАДАЧА 41.
Задача на заміщення
Учень на 37 грн. купив книгу, зошит та олівець. Зошит, ручка і олівець коштують разом 19 грн. Книга, ручка та олівець коштують 35 грн., зошит і олівець - 15 грн. Скільки коштує кожний предмет окремо?
Умовно запишемо так:
Книга+зошит+олівець=37 грн. (1)
Зошит+ручка+олівець=19 грн. (2)
Книга+ручка+олівець=35 грн. (3)
Зошит+олівець=15 грн. (4)
Підставимо (4) в (1) і отримаємо: книга +15=37грн.; звідси вартість книги
37 - 15 = 22 грн.
Підставимо (4) в (2) і отримаємо 15 грн + ручка = 19 грн.
Тоді вартість ручки 19-15 = 4 грн.
З (3) знайдемо вартість олівця: 35 - 22 - 4 = 9 грн.
З (4) знаходимо вартість зошита: 15-9 = 6 грн.
Відповідь: книга коштує 22 грн.; ручка - 4 грн.; олівець - 9 грн., зошит - 6 грн.
ЗАДАЧА 42. (вирішується з кінця)
Дмитрик поїхав до магазину. По дорозі він витратив 2 грн. на проїзд у маршрутному таксі. В магазині половину грошей витратив на продукти харчування. Половину решти витратив на шкільне приладдя та ще 5 грн. на морозиво. На половину того, що залишилося, він купив повітряну кульку і в нього залишилися гроші тільки на зворотній проїзд. Скільки грошей дала мама Дмитрикові?
Намалюємо схему до задачі.
На зворотний проїзд у Діми залишилося 2 грн., тоді повітряна куля коштувала також 2 грн. На шкільне приладдя він витратив 5 + 2 + 2 = 9 грн. Продукти харчування коштували 9·2 = 18 грн. Всього грошей у Діми було 18·2 + 2 = 38 грн.
Відповідь: 38 грн.
ЗАДАЧА 43.
У картинній галереї побувало 550 учнів. Вони проходили 25-ма групами по 20 і 30 школярів. Скільки прийшло груп по 20 і по 30 школярів?
Міркування:
Всього було 25 груп, у кожній групі чи 20 учнів, або 30 учнів. Припустимо, що всі групи були по 20 учнів. Тоді 25·20 = 500 учнів. Залишилося ще 50 учнів, яких треба розділити по цих групах. У групу можна додати ще по 10 учнів, тому буде ще 50 : 10 = 5 груп. Звідси маємо 25 - 5 = 20 груп по 20 учнів та 5 груп по 30 учнів. Дійсно, 20·20 + 5·30 = 400 + 150 = 550 учнів.
Відповідь: 20 груп по 20 учнів та 5 груп по 30 учнів.
ЗАДАЧА 44.
Три мурахи повзуть по дерев’яній метровій лінійці. Коли вони втомилися, мураха Аліса сіла на число 24, мураха Оленка сіла на число 66, а мураха Соломійка - якраз посередині поміж Алісою і Оленкою. На яке число сіла Соломія?
(66 - 24): 2 = 21 - відстань між двома сусідніми мурахами.
24 + 21 = 45 - число, на яке сіла мураха Соломія.
Відповідь: 45.
ЗАДАЧА 45.
На алеї ростуть сосни і берези так, що між сусідніми соснами росте одна береза. Відстань між будь-якими двома деревами дорівнює 3 м. Знайдіть відстань між п’ятою сосною і одинадцятою березою? Між четвертою сосною і дев’ятою березою?
Намалюємо схематично ряд дерев.
Між п’ятою сосною і одинадцятою березою 12 дерев,
12 дерев + сосна + береза, всього 14 об’єктів. Об’єкти, розміщені в ряді, тоді кількість проміжків на 1 менше, ніж самих об’єктів, а отже, 13 відстаней, тому шукана відстань дорівнює 13·3 = 39 м. Аналогічно, відстань між 4-ю сосною і 9-ю березою дорівнює 11·3 = 33 м.
ЗАДАЧА 46. ( на частини)
У Сашка 201 монета. Третина його монет по одній копійці, третина - по 5 копійок, а решта по 10 копійок. Скільки копійок у Сашка?
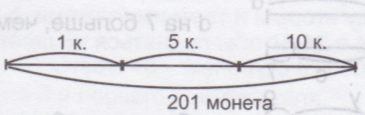
1) 201 : 3 = 67 (монет) - по одній копійці, по 5 копійок і по 10 копійок.
2) 67·1 + 67·5 + 67·10 = 67· (1 + 5 + 10) = 67·16 = 1072 (копійок) у Саші.
Відповідь: 1072 копійок або 10 грн. 72 коп.
ЗАДАЧА 47.
Школярі за два дні зібрали 395 кг яблук. В другий день вони зібрали в 3 рази більше, ніж у перший день і ще 27 кг яблук. Скільки кілограмів яблук зібрали школярі за кожний із днів?
Намалюємо схему до задачі.
Вага зібраних яблук складається з чотирьох рівних частин і ще 27 кг.
1) (395 - 27): 4 = 92 кг яблук в одній частині, або зібрано в перший день.
2) 395 - 92 = 303 кг яблук зібрали у другий день.
Відповідь: 92 кг, 303 кг.
ЗАДАЧА 48.
Три подружки - Віра, Оля і Таня пішли в ліс по ягоди. Для збору ягід у них були кошик, козуб і відерце. Відомо, що Оля була не з кошиком і не з козубом, Віра - не з козубом. Що з собою взяла кожна дівчинка для збору ягід?
|
|
Кошик |
Козуб |
Відерце |
|
Віра |
+ |
- |
- |
|
Оля |
- |
- |
+ |
|
Таня |
- |
+ |
- |
Відповідь. Віра була з кошиком, Оля - з відерцем, Таня - з козубом.
ЗАДАЧА 49.
Один годинник відстає на 25 хвилин, показуючи 1 год 50 хв. Який час показує інший годинник, якщо він забігає на 15 хв?
Відповідь. 1 год 50 хв+25 хв= 2 год15 хв
2 год 15 хв+15 хв=2 год 30хв
ЗАДАЧА 50.
Сашко був у таборі відпочинку з 15 липня по 7 серпня включно. Скільки днів був Сашко у таборі, якщо у липні 31 день.
Відповідь. 24 дні
ЗАДАЧА 51.
10 насосів за 10 хвилин відкачують 1 тону води. За скільки хвилин 20 таких насосів відкачають 2 тони води?
Відповідь. За 10 хвилин.
ЗАДАЧА 52.
У павука 4 пари ніг, а в козеняти — 2 пари ніг. На скільки більше ніг у павука, ніж у козеняти?
Відповідь. На 4 ноги.
ЗАДАЧА 53.
Василько написав на папрці число 89 і сказав Сергійку: «Не виконуючи ніяких записів, зменш число на 21». Сергійко відразу розв’язав задачу. Як він це зробив?
Відповідь. Перевернув папірець.
ЗАДАЧА 54.
На столі лежали 3 цукерки в одній кучці. Дві матері, дві дочки та бабуся з внучкою взяли цукерки по одній штучці, і не стало цієї кучки. Як це зрозуміти? Скільки людей брали цукерки?
Відповідь. 3
ЗАДАЧА 55.
У сітці 5 груш. Як їх поділити між 5 дівчатами, але так, щоб одна груша залишилася в сітці?
Відповідь. Одній дівчинці дати грушу з сіткою.
ЗАДАЧА 56.
Коли матері виповнився 31 рік, донечці було 8. Зараз мама старша за доньку в 2 рази. Скільки їм зараз кожній років?
Коли народилася дочка, матері було 31-8 = 23 роки.
Зараз мати старша в 2 рази, тобто 23х2 = 46 років
За цей час дочка виросла, їй 23 роки.
Відповідь: 23 роки – вік дочки, 46 років – вік матері.
ЗАДАЧА 57.
В трьох вазах 27 троянд. Коли із першої вази переставили 5 троянд у другу, а із другої в третю – 3 троянди, то у всіх вазах квітів стало порівну. Скільки троянд було спочатку в кожній вазі?
Розв’язання.
Кількість усіх троянд не змінювалась, коли їх переставляли. Тому після перестановок у кожній вазі стало 27 : 3 = 9 квітів. Значить у першій спочатку було 9 – 3 = 6 троянд, 9 + 3 – 5 = 7 троянд, а в першій 9 + 5 = 14 .
ЗАДАЧА 58.
Трьом Товстунам принесли 30 тістечок, порівну кожному. Перший Товстун з’їв декілька тістечок, другий з’їв стільки, скільки тістечок залишилось у першого, а третій з’їв стільки, скільки з’їли перший і другий разом. Скільки всього тістечок залишилось у трьох Товстунів?
Розв’язання.
Трьом Товстунам принесли 30 тістечок, порівну кожному. Тобто кожному Товстуну дісталось 30 : 3 = 10 тістечок. Перший Товстун з’їв декілька тістечок, а другий з’їв стільки, скільки тістечок залишилось у першого. Значить, кількість тістечок, які з’їли перший і другий Товстуни разом, дорівнює кількості тістечок, що дісталось першому Товстуну, а це 10.
Третій Товстун з’їв стільки тістечок, скільки з’їли перший і другий разом. Значить він з’їв 10 тістечок.
Три Товстуни з’їли всього 10 + 10 = 20 тістечок, тоді у них залишилось
30 – 20 = 10 тістечок.
ЗАДАЧА 59.
Чотири каченя і п’ять гусят важать 4кг100г, а п’ять каченят і чотири гусеня важать 4кг. Скільки важить одне каченя?
Розв’язання.
Запишемо коротко умову:
4к + 5г = 4100г
5к + 4г = 4000г
Вага 9 каченят і 9 гусят буде разом 8100г, значить, вага одного каченя і одного гусеня дорівнює 8100 : 9 = 900г, тоді вага 4 каченят буде 900 Х 4 = 3600г. Користуючись умовою задачі 4000 – 3600 = 400г – вага одного каченя.
ЗАДАЧА 60.
Коробка цукерок має вагу 800г. Після того, як діти з’їли третю частину, її маса стала 600г. Яка маса порожньої коробки?
Розв’язання.
Якщо після того, як з’їли залишилось 600г цукерок, то третя частина дорівнює 200г. Тоді всі цукерки без коробки важать 600г, а маса порожньої коробки 200г.
ЗАДАЧА 61.
Три брати спіймали 29 карасів. Коли один брат відклав для юшки 6 штук, другий 2 рибини, а третій 3 штуки, то у кожного залишилася однакова кількість риб. Скільки карасів спіймав кожен з них?
Розв’язання.
- 6 + 2 + 3 = 11(риб.) карасів пішло на юшку;
- 29 – 11 = 18 (риб.) карасів залишилось всього;
- 18 : 3 = 6 (риб.) карасів залишилось у кожного ;
- 6 + 6 = 12 (риб.) карасів у першого;
- 6 + 2 = 8 (риб.) карасів у другого;
- 6 + 3 = 9 (риб.) карасів у третього.
ЗАДАЧА 62.
Собака побачив зайця за 150 м від себе. Заєць пробігає за 2 хвилини 500м, а собака за 5 хвилин – 1300м. За який час собака дожене зайця?
Розв’язання.
- 500 : 2 = 250 (м/хв) швидкість зайця;
- 1300 : 5 =260 (м/хв) швидкість собаки;
- 260 – 250 = 10 (м) на 10 метрів зменшилась відстань між зайцем і собаком за хвилину;
- 150 : 10 = 15 (хв)
ЗАДАЧА 63.
У їдальню привезли карпів, сазанів, судаків, лящів. Карпів було 46 кг, сазанів 30 кг, а судаків у 3 рази більше, ніж лящів. Коли половину усієї риби використали, то залишилось 90 кг. Скільки кг судаків привезли у їдальню?
Розв’язання.
- 46 + 30 = 76 (кг) карпів і сазанів;
- 90 х 2 = 180 (кг) усього риби;
- 180 – 76 = 104 (кг) судаків і лящів;
- 104 : 4 = 26 (кг) лящів;
- 26 х 3 = 78 (кг) судаків.
ЗАДАЧА 64.
Господар підрахував, що корова коштує вчетверо більше собаки, кінь вчетверо дорожче корови. Чоловік взяв з собою у місто 200 грн. і на всі гроші купив собаку, двох корів і коня. Скільки коштує кожна тварина?
Розв’язання.
Позначимо, що
Собака – 1 частина;
Корова – 4 частини;
Дві корови 4 х 2;
Кінь 16 частин
- 1+ 4 х 2 + 16 = 25 (частин)
- 200: 25 = 8 (грн.) собака;
- 8 х 4 = 32 (грн.) коштує корова;
- 32 х 4 = 128 (грн.) коштує кінь.
ЗАДАЧА 65.
Маса порося і собаки 64 кг, барана і порося теж 64кг, собаки і барана 60 кг. Яка маса порося?
Розв’язання.
- 60 : 2 = 30 (кг) важить окремо баран і порося;
- 64 – 30 = 34 (кг) важить порося.
ЗАДАЧА 66.
Двоє кухарів почистили 400 картопельок. Один чистив 3 картоплі за хвилину, другий 2. Другий працював на 25 хвилин більше першого. Скільки часу працював кожен?
- 2 х 25 = 50 (шт.)
- 400 – 50 = 350 (шт.)
- 2 + 3 = 5 (шт.)
- 350 : 5 = 70 (хв.)
- 70 + 25 = 95 (хв.)
ЗАДАЧА 67.
На залізничній станції стоять один за одним 7 пасажирських і 20 вантажних вагонів. Довжина усіх вагонів 217 м. Пасажирський вагон на 4 м довше вантажного. Знайди довжину того і іншого вагонів.
Розв’язання.
- 20 + 7 = 27 (ваг.) у всьому составі;
- 7 х 4 = 28 (м) довжина усіх вагонів;
- 217 – 28 = 189 (м) довжина потягу, якщо всі вони вантажні;
- 189 : 27 = 7 (м) довжина вантажного вагону;
- 7 + 4 = 11( м) довжина пасажирського вагону.
ЗАДАЧА 68.
1. Аріна і Настя пішли до магазину. Аріна витратила половину своїх грошей на морозиво, а Настя на половину своїх грошей купила пиріжок. Потім вони на всі гроші, що залишилися купили одну книжку за 40 гривен. Скільки грошей було на самому початку у кожної з дівчат, якщо пиріжок на 10 гривен дешевше, ніж морозиво?
Розв'язання.
Обидві дівчинки витратили половину своїх грошей на морозиво і пиріжок, значить, залишилося у них стільки ж, скільки вони витратили, тобто книга коштує стільки ж, скільки морозиво і пиріжок разом.
М = П + 10. П + П + 10 = 40, П = 15.
15+15=30 гривен було у Насті.
(15+10) • 2=50 гривен у Аріни.
ЗАДАЧА 69.
На майданчику грали 7 дівчаток і 2 хлопчики. Сума років всіх граючих склала 80. Всі дівчатка були однолітки. Одного віку були і хлопчики. Коли в одну групу об'єдналися 5 дівчаток, а у іншу решта, то виявилося, що суми чисел років грають в одній і іншій групах стали рівними. Якого віку були гравці?
Розв'язання.
- 80 : 2 = 40 (років) - сума років п'яти дівчаток;
- 40 : 5 = 8 (років) – вік однієї дівчинки;
- 8 • 7 = 56 (років) - сума років всіх дівчаток;
- 80 - 56 = 24 (року) - сума всіх років хлопчиків;
ЗАДАЧА 70.
На новорічному ранку три подруги, Аня, Віра і Даша, були активними учасниками, одна з них була Снігуронькою. Коли їх подруги запитали, хто ж з них був Снігуронькою, то Аня їм сказала: «На ваше питання кожна з нас дасть свою відповідь. За цими відповідями ви повинні здогадатися самі, хто з нас насправді був Снігуронькою. Але знайте, що Даша завжди каже правду». - «Добре, - відповіли подруги, - послухаємо ваші відповіді. Це навіть цікаво».
Аня: «Снігуронькою була я».
Віра: «Я не була Снігуронькою».
Даша: «Одна з них говорить правду, а інша неправду».
Так хто ж з подруг на новорічному ранку була снігуронькою?
Розв'язання.
З твердження Даші отримуємо, що серед висловлювань Ані і Віри одне істинне, а інше - хибне. Якщо помилковим буде вислів Віри, то отримаємо, що і Аня, і Віра були Снігуроньками, чого бути не може. Отже, помилковим повинно бути вислів Ані. В цьому випадку одержуємо, що Аня Снігуронькою не була, не була Снігуронькою і Віра. Залишається, що Снігуронькою була Даша.
ЗАДАЧА 71.
П'ятачок може свій город перекопати за 12 годин, Вінні-Пух може перекопати цей же город за 4 години. За скільки годин вони перекопають його разом?
Розв'язання.
Вінні-Пух копає в 3 рази швидше П'ятачка. Коли вони перекопають город разом, три частини будуть перекопані Вінні-Пухом і одна - П'ятачком – всього чотири частини. Оскільки Вінні-Пух і П'ятачок почали і закінчили копати одночасно, то весь город вони удвох перекопували стільки ж часу, скільки П'ятачок перекопував свою чверть городу. П'ятачок перекопає цілий город за 12 годин, а чверть городу - за 3 години. Значить, разом друзі копали город 3 години.
Відповідь: за 3 години.
ЗАДАЧА 72.
Дві мухи змагаються, хто швидше заповзе на верхній край склянки і спуститься вниз. Одна муха повзе весь час з однаковою швидкістю, інша вгору повзе в 2 рази швидше першої, а вниз - в 2 рази повільніше першої. Яка муха приповзе вниз першою?
Розв'язання.
Перший спосіб.
Намалюємо склянку і двох мух. Позначимо стрілками їх швидкості. Біла муха повзе весь час з однаковою швидкістю, а чорна повзе в гору в два рази швидше її, а вниз - в два рази повільніше. Коли чорна муха добереться до верхнього краю склянки, біла буде тільки на середині. Тепер чорна муха починає спускатися - повільніше, ніж біла муха, і в чотири рази ніж вона повзла вгору. Біла муха починає спускатися. Середини склянки досягнуто одночасно. Біла муха повзе вниз в два рази швидше, ніж чорна, тому до дна вона доповзе перша.
Другий спосіб.
Перша муха повзе з однаковою швидкістю. Вона забереться вгору за годину Т і спуститься за годину Т. Вся подорож займе у неї годину 2Т. Друга муха забереться вгору в 2 рази швидше, тобто за годину Т : 2, а спускатися буде в 2 рази повільніше першої, це займе у неї годину 2Т.
На весь шлях потрібно Т : 2 + 2Т > 2Т
ЗАДАЧА 73.
Мотоцикліст за три дні проїхав 980 км. За перші два дні він проїхав 725 км, при цьому він на другий день проїхав на 123 км більше, ніж на третій день. Скільки кілометрів він проїхав у кожен з цих трьох днів?
I день _______,
II день _______,
III день ________.
Розв'язання.
1) 980 - 725 = 255 (км) - проїхав у третій день;
2) 255 + 123 = 378 (км) - проїхав у другий день;
3) 725 - 378 = 347 (км) - проїхав в перший день.
Відповідь: у перший день проїхав мотоцикліст 347 км, у другій - 378, у третій - 255 км.
Геометричний матеріал
- Скільки різних трикутників у цій фігурі?
Відповідь. 47 трикутників
- На яке найільше число можна поділити круг трьома прямими?
Відповідь. На 7 частин
- Знайдіть площу затемненої частини прямокутника зі сторонами
2 см і 3 см.
а) 1 см²; б) 2 см²; в) 3 см²; г) 4 см²; д) 6 см².
Відповідь. 3 см²
- Пиріг прямокутної форми поділили двома розрізами на 4 частини так, щоб половина частини була трикутної форми, а друга половина – чотирикутної форми. Намалюйте, як саме поділили пиріг.
Відповідь.
- На прямій є точки А, В, С, D, причому АС=10 см, ВD=15 см, АD=22 см. Знайти довжину відрізка ВС.
А В С D
1 спосіб
- 22 – 10 = 12 (см) – СD;
- 22 – 15 = 7 (см) – АВ;
- 22 – (12+7) = 3 (см)
2 спосіб
(15+10) – 22 = 3 (см)
Відповідь. ВС= 3 см
- Дано прямокутникзі сторонами 12 см і 10 см. Що треба зробити з його довжиною, щоб вийшов квадрат?
Відповідь. Зменшити на 2 см
- Від прямокутного листа фанери відрізали 2 прямокутники. Знайдіть площу отриманої фігури. Скільки фарби потрібно для фарбування фігури з двох сторін, якщо на 1 м² потрібно 18 г фарби?
1) S = 16·9-4·6-6 ·1 = 144-30 = 114 м² - площа фігури
2) 114 · 18 · 2 = 4104 г фарби
Відповідь: 4 кг 104 г фарби
8. На малюнку зображено прямокутну ділянку землі площею 30 м2. Вона поділена на три прямокутні ділянки. Ширина ділянки з квітами - 2 метри, а її площа -10 м2. Ділянка з капустою має ширину 3 м. Чому дорівнює площа ділянки з полуницями?
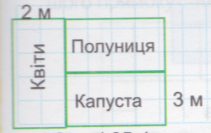
1) 10 : 2 = 5 (м) - довжина ділянки з квітами.
2) 30 - 10 = 20 (м²) площа ділянки з полуницею і капустою.
3) 20 : 5 = 4 (м) - довжина ділянки з полуницею.
4) 4·2 = 8 (м²) площа ділянки з полуницею.
Відповідь: 8 м².
9. Більша сторона прямокутника становить 8 дм 5 см, вона більша від меншої сторони в 5 разів. Яка площа і який периметр прямокутника?
Розв’язання:
85 : 5 = 17 (см) – ширина прямокутника
Р = (85 + 17) · 2 = 204 (см)
S = 85 · 17 = 1445 (см 2)
10. Двома прямими лініями розділи прямокутник на:
- два трикутники і два п’ятикутники;
- два трикутники, чотирикутник і п’ятикутник.
Розв’язання:
11. Роман хоче поділити прямокутник розмірами 6 см х 7 см на квадрати зі сторонами, довжини яких виражаються цілим числом сантиметрів. Яку найменшу кількість квадратів він може отримати?
Розв’язання: На малюнку зображено, як прямокутник розміром 6 см х 7 см можна розбити на 5 квадратів. Легко перевірити, що менше п’яти квадратів отримати неможливо.
12. Прямокутник ABCD поділено на чотири прямокутники так, як це показано на малюнку. Периметри трьох з цих прямокутників дорівнюють 11 см, 16 см і 19 см. Периметр четвертого прямокутника не є найбільшим і не є найменшим. Знайти периметр прямокутника ABCD.
В С
А D
Розв’язання: Зауважимо, що сума периметрів будь-яких двох діагональних прямокутників дорівнює периметру великого прямокутника. Сума найбільшого і найменшого периметрів прямокутників дорівнює сумі периметрів двох інших прямокутників. Р ABCD = 11 + 19 = 30 см.
13. На яке найбільше число можна поділити круг трьома прямими?
Розв’язання
На 7 частин.
14. Скільки трикутників на цьому малюнку?
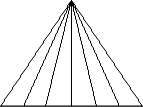(15).
15. У прямокутника, периметр якого дорівнює 30см, ширина в 4 рази коротша за довжину. Знайти довжини сторін прямокутника.
Довжина - 12 см , ширина 3 см .
16. Знайди сторони прямокутника, площа якого дорівнює 12 см, а периметр дорівнює 26 см?
Розв'язання.
Сторони прямокутника :12 см і 1 см
17. Полічіть, скільки трикутників у фігурі, яка зображена на малюнку:
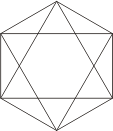32 трикутники.
18. Вовк і Заєць – сусіди по дачі. Довжина спільної сторони дачі 12 м. Цю сторону Заєць загородив парканом, закопуючи через кожні 2 метри стовп. Скільки всього знадобилося стовпів?
Відповідь. 7
ЛІТЕРАТУРА
1. Гісь О. Планета міркувань. Навчальний посібник з розвитку мислення. 4 клас. – Київ: ТОВ «Інститут сучасного підручника», 2013.
2. Гордиюк Н. М. Робота з обдарованими дітьми. Сходинки творчого зростання. 1-4 кл.: Посібник для вчителя. - Тернопіль: Навчальна книга - Богдан, 2007. - с.152.
3. Гуменяк О.В. Спробуй розв’яжи!: Цікаві математичні задачі. - К.: ВЦ «Академія»,1998. - 80 с.
4. Друзь Б. Математична скринька: задачі та цікавинки для молодшого шкільного віку. - К. : «Веселка», 1976. - 108 с.
5. Жаркова І. Система пізнавальних завдань. - Тернопіль: Підручники і посібники, 2004. - 125 с.
6. Збірник задач і тестів з математики. 4 клас. – Тернопіль: Навчальна книга – Богдан, 2009. – 144с.
7. Корчевська О. П. Цікава математика. 1-4 класи . - Тернопіль : Астон. - 2002.
Садова В. С. Готуємось до олімпіади . Олімпіадні завдання з математики для учнів 3-4 класів. - Рівне; Рівненський обласний інститут післядипломної педагогічної освіти, 2014, - 35 с.
8. Логіка. Збірник задач. Початкова школа / Укл. М.О.Володарська. – Х. : Торсінг плюс, 2011. – 256 с.
9. Логические задачи. Рабочая тетрадь. 4 класс. Л.Ф.Шостак, О.Г.Кореновская. Одесса. 2010г. – 72с.
10. Логічна мозаїка. Робочий зошит. 4 клас. /Л.Ф. Шостак, О.Г. Кореновська
Одеса. 2010р. - 72с.
11. Методические рекомендации к пособию «Логическая мозаика» / Л.Ф. Шостак, А.Ю. Мединская, О.Г. Кореновская. 1-4 классы.: Изд. Шостак А.Ф., О.: 2011, 154 с.
12. Олімпіадні завдання з математики для початкових класів / упоряд. Бардакова Ю. Є., Грабовая Г. С., Мінчукова С. І. та ін.. – Х.: Вид. група «Основа», 2005.
13. Олімпіади в початковій школі. М. О. Володарська, Л. І. Охрій. ВГ «Основа» 2016р.
14. Планета Міркувань: навчальний посібник з розвитку мислення для 4 класу загальноосвітніх навчальних закладів – К.: Сучасн. підручники, 2014 – 192с.
15. Сухарєва Л. С. Математичний гурток у початковій школі: орієнтовне планування, розробки занять, дидактичний матеріал. - Х.: Вид. група «Основа», 2003.
16. Предметні олімпіади. 4 клас. Меренцова О.В., Муренець О.Г.
Видавництво Ранок, 2016 р.
17. Чемпіони знань. Цікаві завдання за новою програмою 4 клас. Н. М. Компанець. ВГ «Основа» 2016р.
18. http://ped-kopilka.com.ua/nachalnaja-shkola/didakticheskie-materialy/olimpiadnye-zadanija-s-otvetami-po-matematike-dlja-1-4-klasov.html
19. http://teacher.n-kah.com/dlya-informacii/uchebniie-process/konkursi/bank-ol%D1%96mp%D1%96adnix-zavdan-z-matematiki-4-klas.html
про публікацію авторської розробки
Додати розробку