Збірка нестандартних та прикладних задач

Нестандартні та прикладні задачі

Пішоходи

З місцевостей М і Р, розташованих вздовж однієї дороги, вийшло одночасно на зустріч один одному два пішоходи. Той, хто вийшов з М, йшов з середньою швидкістю v км/год, а той, що вийшов з Р – йшов зі швидкістю w км/год. Перший з них прийшов в Р через  25 год руху після зустрічі з другим пішоходом, а другий – в М через 16 год.

Скільки часу затратив кожен з пішоходів на відстань від  М  до Р?

Розв’язок

Позначимо час, протягом якого пішоходи були в дорозі, через t. Тепер відстань від М до Р можна виразити трьома наступними способами:

(t +25)v=MP                                                          (1)

(t +16)w=MP                                                         (2)

(v+w)t=MP                                                           (3)

З рівняння (1) і (3) маємо:            

(t+25)v=(v+w)t; 

tv+25v =tv+wt;                                                   (A)

25v=wt;

.

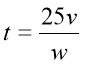З рівняння (2)  і  (3) маємо :        

(t+16)w=(v+w)t; 

tw+16w=tv+wt;                                                 (B)

16w=tv;

.

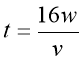Прирівнявши  рівняння  (А)  та  (В)  отримаємо:

;   ;   .

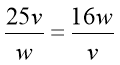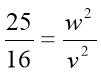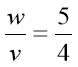Підставивши значення 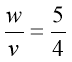  в рівняння  (А) отримаємо .

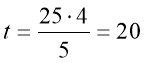Перший пішохід пройшов відстань  з М до  Р  за  25+20=45 годин, а другий за 16+20=36 годин.

Відповідь: 45 годин та 36 годин.

Басейн

На середині басейна знаходиться фонтан. Вода витікає з нього через 16 трубок діаметром см кожна з однаковою швидкістю. Вода з басейну витікає через отвір діаметром 2 см. Одного разу садівник відкрив воду в басейні, але забув закрити зливний отвір. Через скільки годин вода наповнить басейн?

Розв’язок

Басейн ніколи не наповниться водою. Оскільки 16 трубок діаметром см мають загальний переріз, що дорівнює 16· πсм²=π см², а отвір діаметром 2 см має переріз  π·(1 см)² =π см².

Відповідь: ніколи не наповниться.

З вікна вагона

Пасажир, який їде в швидкому потязі зі швидкістю 60 км/год, бачить в вікні вагона зустрічний пасажирський поїзд (середня швидкість якого 40 км/год). Яка довжина пасажирського потягу, якщо пасажир бачив його протягом 6 с?

Розв’язок

Швидкий поїзд проїжджає протягом 1 с шлях, рівний 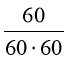  км = км.

Пасажирський за 1 с проходить шлях, рівний 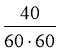              км = км.

За 6 с швидкий потяг проїде відстань км = км, а пасажирський за той же час пройде   км = км. Пасажиру швидкого потягу довжина пасажирського потяга здається коротша його фактичної довжини на стільки метрів, скільки за цей час проїхав швидкий потяг. Тому до шляху, що пройшов швидкий поїзд необхідно додати шлях, що пройшов за той самий час пасажирський поїзд. 

км + км = км = км 166,7 м.

Таким чином довжина пасажирського потягу дорівнює 166,7 м.

Відповідь: 166,7 м.

Хто швидше?

Два хлопчика, Ігор і Максим, навчаються в школі  в сусідньому селі, на відстані 6 км від їхнього селища.

Одного разу автобус, яким вони завжди їздили, зламався і хлопчики вирішили йти пішки. Ігор першу половину шляху йшов зі швидкістю 4 км/год, а другу половину зі швидкістю 2 км/год. Максим вчинив по-іншому, першу половину часу, який затратили на дорогу, він йшов зі швидкістю 4 км/год, а другу йшов 2 км/год.

Хто з хлопчиків прийшов в школу раніше і на скільки?

Розв’язок

Ігор йшов в школу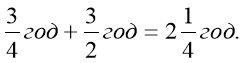 

Максим йшов 6 км  t год. Отже  4км·2км· = 6км, звідси: t=2 год. Тому Максим прийшов в школу раніше на чверть години, ніж Ігор.

Відповідь: Максим на чверть години раніше.

Подорожуючий загін

Туристичний загін відправився з міста на озеро. Біля озера вони відпочили, а потім повернулися в місто. Доріжка, по якій вони йшли, спочатку піднімалася в гору, потім спускалася вниз і нарешті йшла по рівнині. Йдучи в гору, загін йшов зі швидкістю 3 км/год, спускаючись вниз – зі швидкістю 5 км/год, а йдучи по рівнині, туристи проходили 4 км/год. Весь шлях туди і назад зайняв  годин, відстань від міста до озера 12 км. Скільки кілометрів туристи пройшли по рівнині?

Розв’язок

Позначимо:

• довжину доріжки вверх – х к/м;
• довжину доріжки вниз – у к/м; 
• довжину доріжки по рівнині  12–(х+ у) к/м; 

тепер маємо:

       

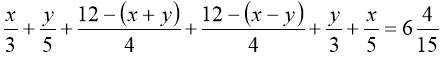
або 

,  

позначимо  х+у=а, отримаємо: 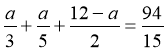, тобто 10а+6а+180–15а=188;  а=8.

Отже по рівнині доріжка проходить

12–а=12–8=4 км.

 Відповідь: 4 км.

Кава з молоком

У мене повний стакан чорної кави. Спочатку я випив одну шосту цієї кави і долив в стакан молоко, щоб стакан знов був повним. Потім я знов випив третину рідини і знову долив молока. Нарешті, я третій раз випив половину стакана і долив ще раз його доверху. Після того я випив свій стакан.

Тепер переді мною стоїть пустий стакан, а я думаю,  чого я випив більше: кави чи молока, скільки я випив всього разом?

Розв’язок

Я випив стакан кави і 

 

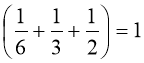
стакан молока.   

Відповідь: стакан кави і стакан молока.

 

 

Відпочинок

Два вихователі виїхали на велосипедах одночасно з однієї бази, щоб доставити плівку з фільмами дітям. Аліна поїхала у табір відпочинку «Сонечко», а Антон – у табір «Усмішка», розміщений від прямої дороги, що веде в «Сонечко». Відстань 7,5 км  від бази до «Сонечка» Аліна проїхала за 0,5 години. Яку відстань проїхав Антон, якщо його швидкість удвічі більша від швидкості  Аліни  і  він   приїхав у  «Усмішку»  на 10 хв пізніше від Аліни?

Розв’язок

Оскільки швидкість Антона у двічі більша від швидкості  Аліни, то він за 0,5 години = 30 хвилин  проїхав відстань вдвічі більшу за відстань, що проїхала Аліна, тобто 0,7·2=15 (км), і за кожні 10 хв він проїжджав  15:3=5 (км). За 40 хв Антон подолав  15+5=20 (км).

 Відповідь: 20 км.

Фабрика

Фабрика  випустила товар у пачках вагою  5  кг  і  3 кг. Довести, що з цих пачок можна скласти пачку будь-якої ваги, більшої за 7 кг.

Розв’язок

Оскільки кожну вагу, яка ділиться на 10, можна скласти з пачок по 5 кг, а кожну вагу, яка ділиться на 3 і 9, можна скласти з пачок по 3 кг, то для справедливості твердження задачі залишається пересвідчитись, що можна скласти з пачок по 5 кг і 3 кг такі ваги: 8 кг, 11 кг, 13 кг, 14 кг, 17 кг.

Це випливає з рівностей:

8=5+3;

11=3·2+5;

13=5·2+3;

14=3·3+5;

17=3·4+5.

На зупинці

Не дочекавшись трамваю на зупинці А, хлопчик пішов до наступної зупинки В. Пройшовши шляху, він озирнувся і помітив, що до зупинки А наближається трамвай. Якщо хлопчик побіжить до зупинки А або до зупинки В, то в обох випадках він встигне сісти на трамвай. З якою швидкістю повинен бігти хлопчик, коли відомо, що трамвай рухається зі швидкістю 30 км/год?

Розв’язок

Якщо хлопчик побіжить до зупинки А, то він пробіжить туди одночасно з проходом трамваю. Через те, що хлопчик від зупинки В був удвічі далі, ніж від А, то, коли він побіжить до В і пробіжить півшляху, трамвай саме підійде до зупинки А. Після цього трамвай і хлопчик одночасно прибувають на зупинку В, але трамвай проходить при цьому шлях, утричі довший, ніж пробігає хлопчик. Отже, швидкість хлопчика дорівнює 10 км/год.

Відповідь: 10 км/год.

Коли наздожене?

Вовк почав наздоганяти Зайця, коли відстань між ними була 100 м.   Заєць  біг  зі швидкістю 0,01 км/с, Вовк – зі швидкістю 0,006 км/с. Після кожних 10 с бігу Заєць відпочивав 10 с. Через скільки секунд Вовк наздожене зайця?

Розв’язок

Швидкість Зайця 0,01 км/с=10 м/с. Швидкість Вовка 0,006 км/с=6 м/с. Заєць за 10 с пробіжить 10·10=100 (м),  а Вовк за  20  с  пробіжить 6·20=120 (м).

Кожні 20 с відстань між зайцем і Вовком скорочується на 120–100=20 (м), тобто кожної секунди відстань між ними зменшується на 1 м. Щоб подолати Вовкові 100 м, потрібно 100 секунд. Отже, Вовк наздожене Зайця через 100 с.

Відповідь: 100 с. 

Капуста

Мама принесла з базару  качан капусти. Батько сказав: «принесла 90% води». Капуста підсохла, батько визначив 40% вологості і зменшення маси на 0,6 кг. Яка була маса капусти спочатку?

Розв’язок

Нехай маса капусти спочатку х кг, тоді води в ній було 0,9х кг. Після того як капуста підсохла, води в ній зменшилось на 0,6 кг і стало (0,9х –0,6) кг. Це становить 40% від маси підсохлої капусти, тобто 0,4(х–0,6) кг. Отже розв’язавши рівняння 0,4(х–0,6)=0,9х–0,6, знайдемо х=0,72. Отже маса капусти 720 г.

Відповідь: 720 г.

 

 

Математика на кухні

Одного разу між поваром та вихователем в літньому таборі  відбулась така розмова:

• Який сьогодні буде суп?
• Смачний.
• Чи багато його буде?
• Найбільше в ньому буде чистої джерельної води, по вазі стільки ж, скільки крупи, картоплі, цибулі та жиру разом
• Ця відповідь мене не влаштовує.
• В цьому разі я ще можу додати, що крупи я взяв стільки ж, скільки картоплі, цибулі та жиру разом.
• А картоплі?
• Рівно стільки, скільки жиру та цибулі.
• А жиру?
• Вдвічі менше, ніж цибулі.
• А постав суп на терези.
• Сім кілограмів, разом з каструлею, яка заважує 1 кг.
• Дякую.

Дуже цікаво, яка вага води, крупи, картоплі, цибулі та жиру, взятих на суп?

Розв’язок

Якщо взяли: води  w кг, крупи k  кг, картоплі  z кг, жиру  t кг,  цибулі  c кг, а разом  вийшло

7–1=6 кг,

тоді

1) w+k+z+t+c=6 кг;

 2) w=k+z+t+c;

 3) k=z+t+c;

 4) z=t+c;

 5) t=c      або         c=2t,

2w=6 кг,    w=3 кг, отже води 3 кг; 

w=2k;    2k=3 кг;    k=1,5 кг, отже крупи 1,5 кг ;

к=2z;    2z=1,5 кг;   z= кг, отже картоплі кг  ;

    z=3t;  3t= кг ;  t= кг, отже знайшли кількість жиру;

    c=2t;   c=0,5 кг.

Відповідь: води 3 кг,  крупи 1,5 кг,  картоплі кг,    жиру кг,    цибулі 0,5 кг             

Туристи

 Перший турист, проїхавши 1,5 години на велосипеді зі швидкістю 16 км/год., робить зупинку на 1,5 години, а потім продовжує рух з початковою швидкістю. Через 4 години після відправлення першого туриста слідом вирушає на мотоциклі другий турист зі швидкістю 56 км/год. Яку відстань вони проїдуть, поки другий турист наздожене першого?

Розв’язок

 Перший турист почав шлях на 4 голини раніше, ніж другий.

 

 

 

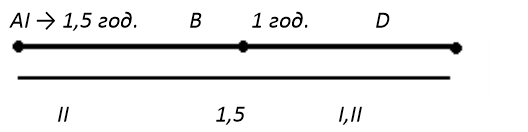
У точці В він зробив зупинку на 1,5 години. Другий турист наздогнав першого в точці D. Щоб проїхати цю відстань, перший турист витратив більше часу, ніж другий на 2,5 години.

Нехай х – відстань від точки А до точки  D. Тоді    годин – час, за який перший турист проїде відстань  AD.    годин – час, за який другий турист проїде відстань AD.

 =2,5 години.

Складаємо і розв’язуємо рівняння: 

=2,5

7х–2х=208

5х=208

х=56 (км)

Відповідь: 56 км

Потяг

 Товарний потяг був затриманий в дорозі на 12 хвилин, а потім на відстані 60 км наздогнав згаяний час, збільшивши швидкість на 15 км/год. Знайдіть початкову швидкість потягу.

 

Розв’язок

 Якби потяг після зупинки продовжував рухатися з початковою швидкістю, то витратив би на 12 хвилин більше, ніж передбачено розкладом.

 

 

 

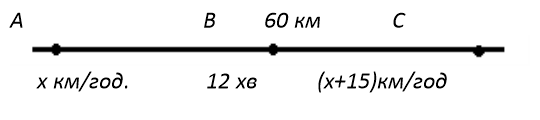
 нехай х – початкова швидкість потягу (в км/год.).  тоді 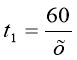 ,  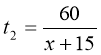,  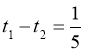,   Складаємо і розв’язуємо рівняння: 

                

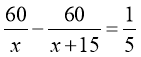
   5∙60(х+15)–5∙60∙х=х(х+15)

   300х+4500–300х= х²+15х

   х²-15х+4500=0

    х²-15х+4500=0

   за т. Вієта  х=60, х=-75 (не задовольняє умову задачі.)

Відповідь: 60 км/год.

Ухилився від відповіді

Робітник копав яму. На питання перехожого, якої глибини буде яма, яку він копає, робітник відповів: «Мій зріст 1 м 80 см. Коли я викопаю яму до кінця, то моя голова буде на стільки нижче рівня землі, на скільки зараз, коли я вже викопав половину, вона знаходиться вище її рівня».

 Якої глибини робітник копає яму?

 

Розв’язок

 Нехай х – глибина ями, яку копає робітник, а у – висота виступаючої голови над ямою, в момент, коли яма викопана на половину. Тоді

       +у=180;      х–у=180   

з цих рівнянь отримуємо:

      х = 360;   х = 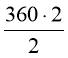= 2 м 40 см.

Відповідь: 2 м 40 см.

Лисиця і вівчарка

Вівчарка погналася за лисицею, коли між ними була відстань 99 м. Стрибок лисиці 1,1 м, а вівчарки – 2,2 м. Коли вівчарка робить 19 стрибків, лисиця робить 29.

Скільки метрів прострибають вони, перш ніж вівчарка наздожене лисицю?

Розв’язок

 Нехай 19х – кількість стрибків вівчарки, а 29у – лисиці, тоді        19х·2,2–29у ·1,1=99  

41,8х–31,9=99   (поділимо на 1,1)

 38х–29у=90, звідки найбільш правдиві значення   х=10, у=10.  Тоді 19х=190 (стрибків),   29у=290 (стрибків). 190·2,2=418 (м), 290·1,1=319 (м).

  Відповідь: Вівчарка прострибає 418 м, лисиця – 319 м.

Повітряна куля

Землю як на долоні, коли ти в небі на повітряній кулі. Як далеко видно з повітряної кулі, що піднялася на висоту 4 км над Землею (радіус Землі приблизно 6370 км)?

Розв’язок

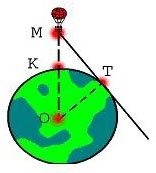
1. за теоремою про дотичну до кола, дотична перпендикулярна радіусу, що проведений в точку дотику, тобто < OTM=90˚.  МО=6370+4=6374 (км).  Тоді за теоремою Піфагора

   MT²+OT²=MO²
  MT²=MO²–OT²
                    
  MT=112,9 км

Відповідь: 112,9 км.

На лузі

 На лузі паслися 90 телят і гусей. Всього було 236 ніг. Скільки було телят і скільки було гусей?

Розв’язок

 Нехай на лузі паслось х телят, тоді гусей було 90–х. оскільки кожне теля має чотири ноги, то всього ніг у телят 4х. у кожній гуски дві ноги, то всього у гусей було 2(90-х) ніг, а у телят і гусей разом було 4х+2(90-х) ніг. Складаємо і розв’язуємо рівняння :

 4х+2(90-х)=236

4х+18 –2х=236

2х=56       

х=38  - телят   і   90–38=52   гуски.

Відповідь: 38 телят і 52 гуски.                

В магазині

 У магазин привезли борошно у 4 мішках. У першому, другому і третьому мішках разом не менше 60 кг борошна; у першому, другому і четвертому разом – не більше 40 кг,  а в другому, третьому і четвертому разом – не більше 30 кг. Скільки борошна у кожному мішку?

Розв’язок

 Позначимо масу борошна у мішках відповідно  x, y, z, p.  тоді маємо:   x+y+z60,

                                      x+y+p50,

                                      x+z+p40,

                                      y+z+p30.

 Звідси   2x+2y+2z+3p120,    2x+2y+2z120 , отже  p=0, тобто четвертий мішок порожній. Тоді  x+y+z=60, отже, x+y=50;  x+z=40;  y+z=30.  Звідси   x=30,   y=20,   z=10,  p=0.

Відповідь: один мішок порожній, інші 30 кг, 20 кг і 10 кг.

Скільки років?

 Батько в 5 разів старший за сина. Батько закінчив інститут у 22 роки. З тих пір пройшов час, що дорівнює половині того, який потрібен синові, щоб йому стало теж 22 роки. Скільки років зараз синові і скільки – батькові?

Розв’язок

 Якщо синові х років, то батькові 5х років. З того часу, як батько закінчив інститут, минуло 5х – 22 роки. Синові до 22 треба ще 22–х років. За умовою (5х-22)∙2=22–х. розв’язуючи це рівняння отримуємо х=6. отже синові – 6 років, батькові – 30 років.

Відповідь: синові 6 років, батькові 30 років.