Презентація " Активізація пізнавальної діяльності учнів на уроці математики"
В данной презентации представлены теоретические материалы и практические наработки по активизации деятельности учащихся. Может быть полезной для подготовки и проведения семинара, педсовета или мастер-класса.

































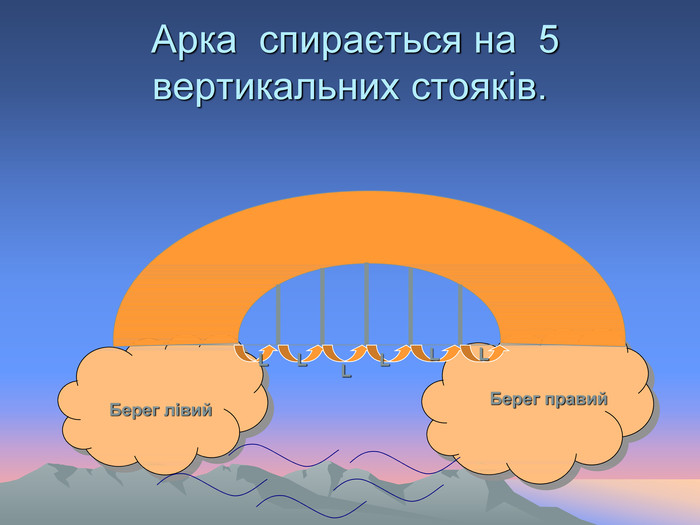
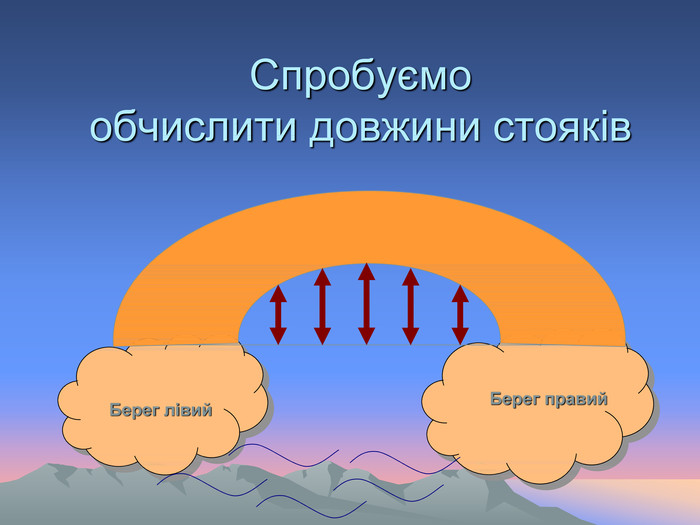
![Считай, что численность войска составляет, например, 100000 человек, объем горсти имеет порядок 0,2 куб. дм., а угол при основании холма равен 45°. Вторая часть задачи: положив рост царя 1,7 м, определить как далеко “царь мог с вышины с весельем озирать”. [18] Считай, что численность войска составляет, например, 100000 человек, объем горсти имеет порядок 0,2 куб. дм., а угол при основании холма равен 45°. Вторая часть задачи: положив рост царя 1,7 м, определить как далеко “царь мог с вышины с весельем озирать”. [18]](/uploads/files/937/5222/5259_images/39.jpg)



































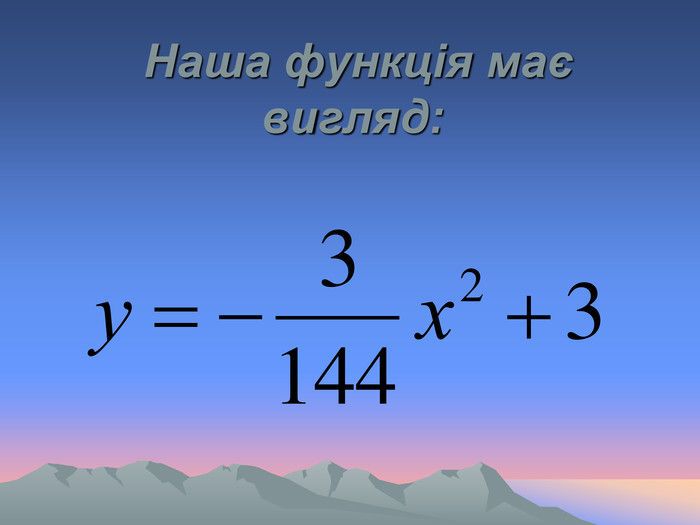




Находясь на воспроизводящем уровне познавательной активности, учащийся должен научиться воспроизводить при необходимости полученные знания или умения. Название интерпретирующего уровня позна-вательной активности говорит само за себя: уже имея некоторые знания, необходимо научиться интерпретировать, или трактовать их в новых учебных условиях, отталкиваясь от привычных образцов. Творческий уровень познавательной активности характерен для учащихся, которые не только усваивают связи между предметами и явлениями, но и пытаются найти для этой цели новый способ.
Познавательный интерес – избирательная направленность личности на предметы и явления окружающей действительности. Эта направленность характеризуется постоянным стремлением к познанию, к новым, более полным и глубоким знаниям. Систематически укрепляясь и развиваясь познавательный интерес становится основой положительного отношения к учению.
Перед учителем стоят следующие задачи: 1. создание на уроках математики условий для активизации познавательной деятельности учащихся; 2. формирование и развитие общеучебных, самостоятельных, познавательных навыков учащихся; 3. создание условий для добывания знаний из реальной жизни, для овладения различными методами действий в нестандартных ситуациях; 4. способствование выработке знаний и умений планирования, целе-направленности, анализа, самооценки познавательной деятельности у учащихся.
Можно сформулировать следующие особенности учебных игр: • в ходе учебной игры учащиеся овладевают опытом деятельности, сходным с тем, который они получили бы в действительности; • учебная игра позволяет учащимся самим решать трудные проблемы, а не просто быть наблюдателями; • игры создают потенциально более высокую возможность переноса знаний и опыта деятельности из учебной ситуации в реальную; • учебные игры обеспечивают учебную среду, незамедлительно реагирующую на действия учащихся.
Приемы развития познавательной активности: • создание ситуации, в которой ученик должен обосновывать свое мне-ние, приводить в его защиту аргументы, факты, использовать приобре-тенные знания и опыт; • создание ситуации, побуждающей учащегося задавать вопросы препо-давателю, товарищам, выяснять неясное, глубже осмысливать знания; • рецензирование ответов, сочинений, творческих работ, что связано с советами, коррективами, активными поисками главного; • оказание помощи товарищам при затруднениях, объяснение неясного; • выполнение заданий-максимумов, рассчитанных на чтение дополни-тельной литературы, научных источников и другой поисковой деятель-ности; • побуждение к поиску различных способов решения задачи, рассмотре-нию вопроса с различных точек зрения; • создание ситуации свободного выбора заданий; • создание ситуаций обмена информацией между учащимися; • создание ситуации самопроверки, анализа собственных знаний и прак-тических умений.
Школьная математика должна включать в себя обе ветви современной математики (теоретическую и прикладную). Под прикладной обычно понимается тот раздел математики, в котором демонстрируется применение математической теории в практических ситуациях. В школьном курсе математики при решении прикладных задач естественным этапом является математическое моделирование реальных процессов.
Сформулируем некоторые требования к прикладным задачам: в содержании задач должны отражаться математические и нематематические проблемы и их взаимная связь; прикладные задачи должны соответствовать программе курса; содержащийся в задаче прикладной материал должен вводиться в процесс обучения как необходимый компонент, логическое продолжение курса и служить достижению целей обучения; вводимые в содержании прикладных задач понятия, термины, ситуация, методы решения должны быть доступными для учащихся; прикладные задачи, рассматриваемые в школьном курсе математики, могут быть эффективно использованы с разными целями: обучение и развитие.
Учитель в современной школе может и должен обогатить содержание учебного материала задачами прикладного характера. Ведь решение таких задач показывает практическое применение математического аппарата, изучаемого в школе, тем самым пробуждает интерес у учащихся к изучению предмета. Математика становится “нужной” ученику. Из положительных моментов также стоит отметить, что, решая подобные задачи на уроках математики, мы естественным путем осуществляем функцию интеграции школьных предметов.
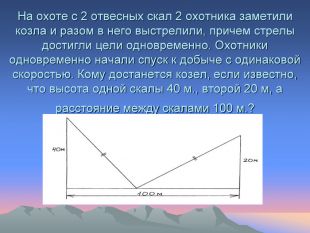
На охоте с 2 отвесных скал 2 охотника заметили козла и разом в него выстрелили, причем стрелы достигли цели одновременно. Охотники одновременно начали спуск к добыче с одинаковой скоростью. Кому достанется козел, если известно, что высота одной скалы 40 м., второй 20 м, а расстояние между скалами 100 м.?
Основной формой обучения в школе является урок Уроку отводится не менее 90% учебного времени. Каждый школьник за годы своего ученичества посетит почти 10000 уроков "Учитель готовится к хорошему уроку всю жизнь...Такова духовная и философская основа нашей профессии и технологии труда: чтобы дать ученику искорку знаний, учителю надо впитать целое море света.“ В.А. Сухомлинский
Познавательная активность включает: 1.Мотивы и цели деятельности. 2.Интерес к предмету. 3.Внимание к изучаемому объекту. 4.Волевые усилия. 5.Положительные эмоции. 6.Творческую самостоятельность. 7.Владение необходимыми способами и приёмами познавательной деятельности. 8.Оптимальный ритм и режим работы, обеспечивающей полное овладение нужными знаниями, умениями и навыками.
Метод проблемного обучения составляет органическую часть системы проблемного обучения. Основой метода проблемного обучения является создание проблемных ситуаций, формулировка проблем, подведение учащихся к проблеме. Проблемная ситуация включает эмоциональную, поисковую и волевую сторону. Её задача - направить деятельность учащихся на максимальное овладение изучаемым материалом, обеспечить мотивационную сторону деятельности, вызвать интерес к ней.
Метод алгоритмического обучения. Для построения алгоритма (программы) решений той или иной проблемы нужно знать наиболее рациональный способ её решения. Рациональными способами решения владеют самые подготовленные и способные ученики. Поэтому для описания алгоритма решения проблемы учитывается путь его получения этими учащимися. Для остальных учащихся такой алгоритм будет служить образцом деятельности.
Работа алгоритмическим методом подразделяется на три шага. Подготовка к работе списка указаний. Хорошо учащихся подводить к его самостоятельному составлению. Образец ответа, предлагаемый учителем. Он последовательно читает указания и одновременно решает задачу. Аналогичным образом работают учащиеся. Они читают указания и решают задачу. При этом они руководствуются как образцом ответа, так и списком указаний.
Метод эвристического обучения. Одной из основ эвристического обучения является решение нестандартных (для учащихся) задач и упражнений. В процессе их решения у учащихся нужно сформировать познавательные стратегии, которые помогали бы находить нужную информацию, преобразовывать её, вырабатывать правила действий в непривычных условиях, формировали бы творческих характер мышления.
Д. Пойа формулирует общие правила, которые лежат в основе поиска решения задачи, следующим образом: Сначала нужно понять задачу. С этой целью целесообразно выполнить чертёж, ввести удобные обозначения, внимательно изучить условия и требования задачи, разделить условие на части Составить план решения, найти связь между данным и неизвестным. На этом этапе задаём учащимся такие вопросы: не встречалась ли ранее подобная задача? Известна ли вам какая-нибудь родственная задача? Нельзя ли ею воспользоваться? Нельзя ли придумать более простую похожую задачу? Нельзя ли решить только часть задачи, отбросив часть условий. Нельзя ли сформировать условие задачи иначе? Реализация плана при контроле за каждым своим шагом. Если результат получен, то нужно проверить его и подумать, нельзя ли его получить другим способом. Эксперименты показывают, что этой схемы можно придерживаться при условии, если у учащихся сформированы приёмы познавательной деятельности- анализ, перенос, аналогия, обобщение, конкретизация, абстрагирование и др.
Метод исследовательского обучения В нестандартных (для учащегося) условиях используется: а) чертеж или модель, которая характеризует свойства объектов исследований; б) индуктивное построение гипотез как абстракций на основе наблюдений, проверка полученных результатов; в) анализ гипотез.
Разминка Соперник нолика. Очень плохая оценка знаний. Есть у любого слова, у растения и может быть у уравнения. 1. Петух на одной ноге весит 4 кг. А на двух? 2. Половина – треть числа. Какое это число? 3. В семье 5 сыновей и у каждого есть сестра. Сколько детей в семье? 4. Кирпич весит 1,5 кг и ещё полкирпича. Какова масса кирпича? 5. Одна кастрюля вдвое выше другой. зато вторая вдвое шире первой. к какую из них больше войдет воды?
ВИЕТ Кто такой Виет? Какой вклад он внес в алгебру? Помимо того, что Ф. Виет – отец современной алгебры, он любил разгадывать зашифрованные письма. Во время войны Франции с Испанией всю тайную переписку испанцев свободно читали французы, так как Виет всякий раз разгадывал испанский шифр. Не представляя себе всего могущества человеческого ума, испанцы думали, что французам помогает дьявол.
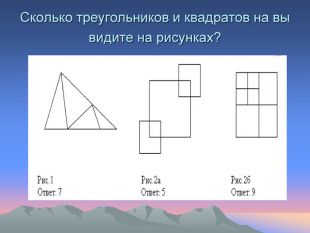
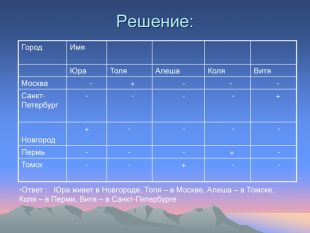
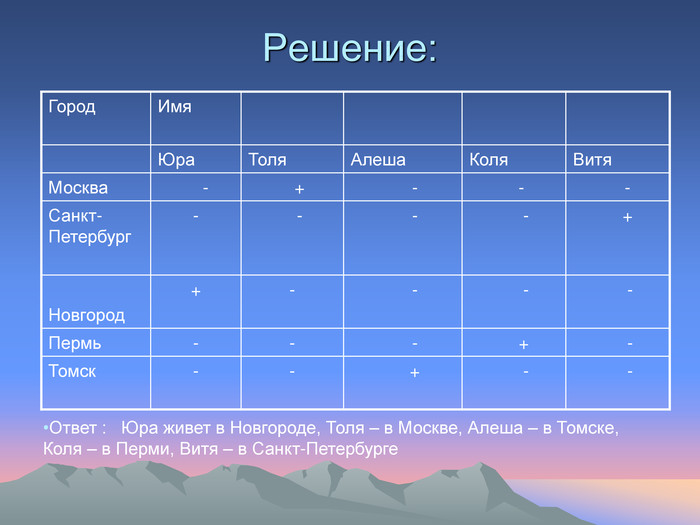
Решение логических задач с помощью таблицы “На конкурсе”. Однажды на конкурсе за круглым столом оказалось пятеро ребят родом из Москвы, Санкт-Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алёша, Коля и Витя. Известно, что: 1. Петербуржец сидел между Юрой и Толей, а напротив него сидели пермяк и Алёша; 2. Коля никогда не был в Санкт-Петербурге; 3. Юра не был в Москве и Томске; 4. Томич с Толей регулярно переписываются. Определите, в каком городе живет каждый из ребят.
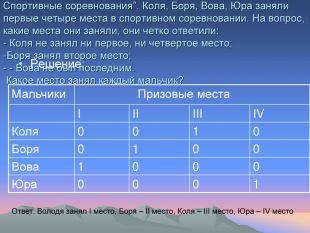
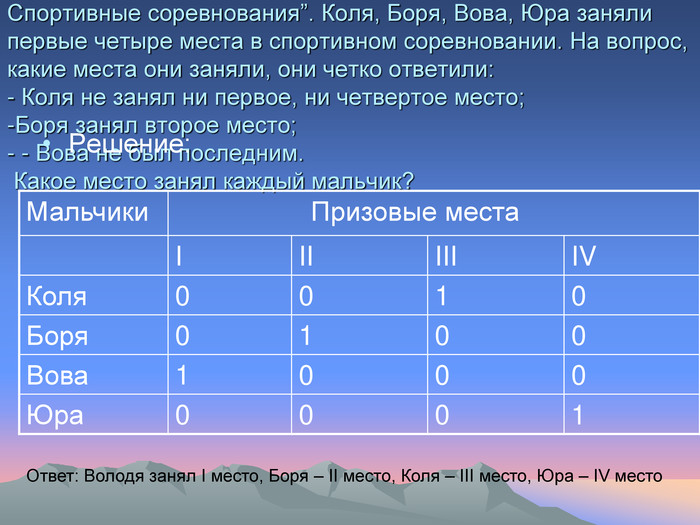
Спортивные соревнования”. Коля, Боря, Вова, Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они четко ответили: - Коля не занял ни первое, ни четвертое место; -Боря занял второе место; - - Вова не был последним. Какое место занял каждый мальчик? Решение: Мальчики Призовые места I II III IV Коля 0 0 1 0 Боря 0 1 0 0 Вова 1 0 0 0 Юра 0 0 0 1 Ответ: Володя занял I место, Боря – II место, Коля – III место, Юра – IV место
Легкий способ умножения первых десяти чисел на 9: Положите обе руки рядом на стол и вытяните пальцы. Пусть каждый палец по порядку означает соответствующее число: первый слева - 1, второй за ним - 2, третий - 3 и т.д. до десятого, который означает 10. Требуется теперь умножить любое из первых десяти чисел на 9. Для этого вам стоит только, не сдвигая рук со стола, приподнять вверх тот палец, который обозначает множимое. Тогда остальные пальцы, лежащие налево от поднятого пальца, дадут в сумме число десятков, а пальцы направо - число единиц.
«Логические заморочки» Какие из высказываний верны? Шмурдик боится как мышей, так и тараканов. 1.шмурдик не боится тараканов; 2.шмурдик боится мышей; 3.шмурдик боится мышей больше, чем тараканов, но и тараканов боится тоже. Известно, что грымзик обязательно или полосат, или рогат, или то и другое вместе. 1.грымзик не может быть безрогим; 2.грымзик не может быть однотонным и безрогим одновременно; 3.грымзик не может быть полосатым и безрогим одновременно.
Забавные задачки Как остановить воровство? В те далекие времена, когда устраивали приемы, приглашали множество гостей и т.д. Так вот, после таких гуляний, у одного графа Х постоянно пропадали ложечки серебрянные, они были сделаны специально по его заказу у известного мастера,каждая ложечка была просто произведением искусства и не удивительно, что они всем безумно нравились, каждый бы не против был иметь такие и у себя дома, поэтому находились такие, которые просто воровали ложечки, а потом у себя дома хвастались ею перед своими гостями. Графу это понятное дело не нравилось, после каждого приема ложечек становилось все меньше и меньше. Что же придумал граф, какой он нашел выход из сложившейся ситуации? Ответ: Граф отнес ложечки к граверу и на каждой было написано не просто его инициалы, а "Украдено у графа Х"
Самодержавный правитель одного острова хотел воспрепятствовать тому, чтобы на острове поселились пришельцы. Желая соблюсти видимость справедливости, он издал распоряжение, согласно которому всякий, желающий поселиться на острове, должен, хорошо поразмыслив, высказать любое предложение, причем после предварительного предупреждения, что от содержания этого предложения зависит его жизнь. Распоряжение гласило: "Если пришелец скажет правду, его расстреляют. Если он скажет неправду, его повесят". Как пришелец, став жителем острова, сохранит свою жизнь?
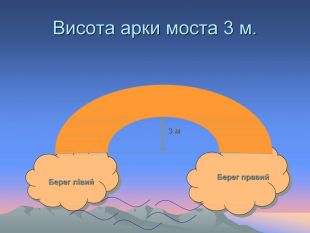
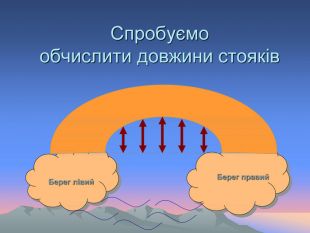
Старинные задачи Основание Карфагена Об основании города Карфагена существует древнее предание. Дидона, дочь тирского царя, потеряв мужа, убитого ее братом, бежала в Африку. Там она купила у нумидийского царя столько земли, "сколько занимает воловья шкура". Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря такой уловке охватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, а впоследствии был построен и город. Попробуйте приблизительно определить, какую площадь могла, согласно этому преданию, занять крепость, если считать, что размер воловьей шкуры 4 кв. м., а ширина ремешков, на которые Дидона ее разрезала, 1 мм.
Ответ: Если площадь воловьей шкуры 4 кв. м. (или 4 млн. кв. мм.), а ширина ремешков 1 мм., то общая длина вырезанного ремня (Дидона, надо думать, вырезала его спирально) - 4 миллиона миллиметров, или 4000 метров, т.е. 4 км. Таким ремнем можно окружить квадратный участок 1 кв. км. и круглый - в 1,3 кв. км
Задания для развития мышления( 6 класс) Как называются числа а и в, если а+в=0? Сравни их модули. Может ли разность быть больше чем уменьшаемое? В каком случае? Приведите примеры. Петя от числа 25,6 отнял число 32,8, а Марийка к числу 12,1 прибавила какое-то число так, что результат у них получился одинаковым. Какое число прибавила Марийка? Дед Панас занял у шинкаря 12 гривень, затем отдал ему 17 гривень, затем снова занял некоторую сумму,и, отдав шинкарю 25 гривень, остался ему должен еще 5 гривень. Какую сумму занял дед Панас во второй раз?
Использование эпиграфов к урокам "Математику уже затем учить надо,что она ум в порядок приводит". (М.В.Ломоносов) "Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью" ( Л.Н.Толстой) «Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать. (Р.Декарт) « Посредством уравнений, теорем я уйму разрешу проблем.» (Чосер )
Использование жизненного опыта учащихся Практические работы Опорные схемы Карточки-информаторы Составление задач по краткой записи с использованием данных из жизненных и школьных ситуаций (“Сколько детей сидело за праздничным столом, если после праздника на клеенке осталось 24 дырки и известно, что на каждой вилке 4 зубца?” )
Вопросы по стереометрии Почему трехколесный велосипед в неподвижном состоянии устойчивый, а двухколесный- нет? В землю вбили 3 столбика разной высоты. Всегда ли на них можно положить лист фанеры? Можно л разрезать торт на восемь частей, проведя только три разреза? При помощи двух шнуров столяр определяет, лежат ли концы четырех ножек стола в одной плоскости. Как он это делает? По каждой из двух скрещивающихся ниток ползет по два паучка. Могут ли они оказаться в одной плоскости? Деревянный куб распилили на две части( с верхнего основания до нижнего). Какую фигуру получили в сечении? Как с помощью линейки проверить вертикальность столба? Как размещен канат в спортзале относительно стены? А относительно пола?
Рефлексивный алгоритм: "Я" + "МЫ" = "ДЕЛО" "Я" (как чувствовал себя, с каким настроением работал, доволен ли собой, какую пользу сегодня извлек). "МЫ" (комфортно ли было работать, какие затруднения были в общении, были ли моменты радости, почему?). "ДЕЛО" (достиг ли цели учения, какие затруднения возникли, как преодолеть свои учебные трудности, о чем хотелось бы поговорить подробнее)
”Учить не мыслям, а мыслить!” И.Кант «Учитель, который хочет принести пользу всем своим учащимся и тем, которые будут и тем, которые не будут пользоваться математикой после школы, должен обучать решению задач так, чтобы обучение на одну треть было математикой, а на две трети здравым смыслом.» (Д. Пойа)


про публікацію авторської розробки
Додати розробку