Збірка нестандартних уроків з математики для учнів 5-6 класів
У збірці зібрані розробки нестандартних уроків з досвіду вчителів математики для учнів 5-6 класів. Збірка складалась мною, як додаток до дипломної роботи, кожен урок ретельно підбирався, щоб відповідати темі дипломної роботи.
1
Збірка
нестандартних уроків математики в 5-6 класах
(досвід роботи вчителів)
ЗМІСТ
5 клас
- Перший урок математики. Вчитель математики ЗОШ І–ІІІ ступенів 2
№ 87 ім. О.Довженка, м. Київ Наталія Литвин.
- Кут та його елементи. «Осінній бал» Вчитель математики гімназії 8
№ 14 м. Луцьк – І.К. Панащук.
3. Додавання і віднімання десяткових дробів. Урок залік. Вчитель 12 математики ЗОШ І – ІІ ступенів № 268, м. Київ – Л.С. Боровська.
4. Урок на всі дії з десятковими дробами. «З Любов’ю до рідного краю» 16
Вчитель математики с. Грузьке, Макарівського району, Київської області
І.С. Ступак.
5. Звичайні дроби. Розв’язування вправ. Вчитель математики 20 Червоногранітянської ЗОШ І – ІІ ступенів Володимир – Волинського району Житомирської області. М.В.Ночевчук.
6 клас
- Перший урок математики в 6-му класі. Урок – змагання. Вчитель 30
математики СШ № 9 м. Фастів, Київської області. Л.О. Командирова.
- Додавання і віднімання звичайних дробів. Урок узагальнення знань. 35
«Математичний бій». Вчитель математики ЗОШ І –ІІІ ступенів № 268, м. Київ Л.С. Боровська.
8. Додатні і від’ємні числа. Прямокутна система координат. 39 «Навколосвітня регата» - дидактична гра. З серії ігор розроблених студентами фізико-математичного факультету Сумського державного педагогічного інституту ім. А.С.Макаренка. С.Бурчак. Ю.Прокопенко.
9. Множення звичайних дробів. Урок – залік. Вчитель – методист 47 загальноосвітнього навчального закладу № 4, м.Рівне. Г.Т. Семенюк.
10. Дії з десятковими дробами. «Щасливий випадок». Вчитель 55
математики й інформатики Колегіуму мистецтв, с.Опішне, Заньковецького району, Полтавської області. Л.М.Сиволга.
Приклад 1. Перший урок математики в 5 класі. Вчитель математики ЗОШ І-ПІ ступенів № 87 ім. О. Довженка, м. Київ Наталія Литвин.
(Урок проводить у формі діалогу. Учитель розказує казку, бесідує з учнями, ставить запитання, відразу оцінюючи для себе рівень їх математичного та загального розвитку).
Казка про те, як на Землі виникли числа.
А чи знаєте ви, що колись дуже давно, мільйони років до нашої ери, коли на Землі ще жили динозаври, а мавпи ще не повністю перетворилися
на людей, вже існувала математика? Звичайно математики як науки ще не було, але без лічби вижити прадавнім людям було б неможливо.
Протягом багатьох років навчання в школі на уроках математики будемо не одноразово повторювати таке висловлення - «математика виникла із потреб людини». Спробуємо це довести.
Найголовніша потреба людини в житті - це саме існування людини. А, як ви розумієте, без їжі людина не може існувати. Отже математика виникла тому, що людям хотілося їсти. Уявімо таку ситуацію. Чоловіки первісного племені збираються на полювання.
Треба знайти і вбити мамонта, щоб було що їсти всьому племені на обід. У розвідку посилають одного представника племені, у якого найгостріший слух і очі бачать найкраще. Решта чекає у засідці. Піднімається розвідник на невеличку гірку і бачить у долині одного мамонта. Як розвідник може показати своїм друзям, що мамонт один? Попереджаю, кричати не можна, мамонт зреагує на крик і тоді вже невідомо, хто стане чиїм обідом. Пальці у первісних людей ще не розвинені, отже показати один палець він не може. То як бути? Ваші пропозиції... (учні в основному пропонують розвіднику підняти руку вгору). А чому саме вгору? Подумайте, що на світі лише тільки в одному екземплярі. Причому воно було одне і мільйони років до нашої ери, одне воно і нині, (учні майже відразу знаходять відповідь - це сонце.), отже, робимо висновок, що розвідник, піднімаючи руку, показував на небо, де вдень люди бачили одне сонце, а вночі - один місяць.
Якщо мамонтів було два? Як показати членам племені, що причаїлися внизу під горою, що мамонтів два? ( Учні пропонують підняти дві руки.), я погоджуюся з вами, але не думаю, що розвідник не просто підняв руки вгору, а виконував руками рухи, схожі на рухи крил. Бо в епоху динозаврів жили літаючі ящери, у яких було два крила. Може, хто-небудь знає, як вони називалися. (Учні називають хижаків, про яких дивилися фільми, читали книжки).
Продовжимо міркування: а якщо було три мамонти? Що на Землі завжди в такій кількості? (Учні доходять висновку, що таких речей не існувало і не існує.) щоб зрозуміти суть, спочатку потрібно пригадати казки. Вчитель читає фразу, а учні її закінчують:
- «І було у царя ... сини»;
- «Можеш загадати тільки ... бажання»;
- «Було у Змія - Горинича ... голови »;
Вас ніколи не дивувало, що в різних казках різних народів світу йдеться про одну й ту саму кількість дітей у правителів, голів у всіляких потвор, бажань, що виконувалися Доброю Силою. Навіть Бог у нас триєдиний. Чому? Тому що довгий час число три вважалося граничним числом. Тобто люди рахували так: один, два, багато. І все, що було більше, ніж два, мало назву - три.
Перед тим, як перейти до числа чотири, повторимо про математичні дії. (діти називають їх). А яка дія з'явилася першою? (діти впевнено кажуть, що «додавання», але довести не можуть). Пригадаємо фразу: «Математика виникла із потреб життя людини». Повернемося до мисливців. Полювання було вдалим, мамонта вбили, підсмажили, залишилося з'їсти. Людей в племені багато. Що робити з підсмаженим мамонтом? Діти відповідають, звичайно, розділити. Отже першою з'явилась дія ділення. В даному випадку ділимо на кількість людей у племені. Чому не можна ділити на нуль? Виходить, що ділити нікому -людей немає, тому ділення на нуль неможливе.
Повернемося до числа чотири. Воно не відіграло такої значної ролі, як число 3, але відомо, що воно було улюбленим числом римського імператора Карла IV. За часів свого правління він збудував 4 палаци, мав екіпаж, запряжений 4 кіньми, він мав 4 дітей, знав 4 мови, якими був написаний його заповіт.
Число п'ять - рідне нам і дуже близьке, бо завжди з нами. Наші руки - наша перша рахівниця у народів Крайньої Півночі збереглась звичка лічити п'ятірками. Так вони рахують своїх оленів, загинаючи пальці спочатку на руках, а потім і на ногах.
Про число шість треба говорити з повагою, бо воно носить назву -досконале число. Досконалі числа - це числа, які дорівнюють сумі своїх дільників, крім самого себе. 1+2+3=6.
Сім - це ще одне граничне число, як і число 3! Пригадаємо деякі прислів'я та приказки: «Сім раз відміряй - один раз відріж», «Семеро одного не чекають», «семеро з сошкою, один з ложкою» тощо. Чи задумувались ми, чому скрізь зустрічається число 7? Не 6, не 8, а саме 7. пояснення цьому сягає в давнину. Саме 7 яскравих точок - планет -бачили давні люди на небосхилі, коли ще вони поклонялися всьому, від чого залежало їхнє життя. Тому в тижні 7 днів, а в народних казках герої завжди ходять шукати щастя за «сім морів» або на «сьомому небі».
Поговоримо про число вісім. Не любили його прадавні люди і називали числом «смерті». Причина ось яка. Запишемо таблицю множення на 8 та додамо цифри в добутках:
1*8=8 8=8 8
2*8=16 1+6=7 7
3*8=24 2+4=6 6
4*8=32 3+2=5 5
5*8=40 4+0=4 4
6*8=48 4+8=12 1+2=3 З
7*8=56 5+6=11 1+1=2 2
8*8=64 6+4+10 1+0=1 1
Як бачимо, сума цифр добутків зменшується на одиницю при збільшенні першого множника на одиницю. Стародавні люди вважали цю закономірність поганою ознакою і навіть філософствували з цього приводу: «Чим більше ми живемо, тим ближче до смерті».
А от число дев'ять вважали числом стабільності та гармонії. Це можна побачити з такої історії. Запропонувала учителька дітям удома вивчити табличку множення на 9. А Миколка пробігав увесь день на вулиці і не зробив домашнього
завдання. На наступний день вчителька викликає Миколку до дошки, де
записано приклади:
2*9= 6*9=
3*9= 7*9=
4*9= 8*9=
5*9= 9*9=
І пропонує записати відповіді. Дивиться Миколка на дошку і не
знає, що писати, бо не вивчив таблички. Тоді думає: « а дай полічу,
скільки відповідей не знаю». І почав лічити зверху:
2*9=1 6*9= 5
3*9=2 7*9= 6
4*9=3 8*9= 7
5*9=4 9*9=8
«Аж 8 відповідей не знаю. Може десь помилився. Спробую полічити
ще раз» - думає Миколка.
2*9=18 6*9=54
3*9=27 7*9=63
4*9=36 8*9= 72
5*9=45 9*9=81
«Все одно аж вісім не знаю. Зараз вчителька буде сваритися». А вона каже: «Молодець!». Надалі Миколка вирішив більше так не випробовувати долю.
Ось як «красиво» можна вивчити таблицю множення на 9. але на нас чекає
ще одне відкриття. Додамо цифри в добутках.
1+8=9 5+4=9
2+7=9 6+3=9
3+6=9 7+2=9
4+5=9 8+1=9
Як бачите, не дарма наші пращури вважали число 9 символом стабільності та мудрості.
Наступне число 10. Складається воно з двох цифр. Яких? Скільки цифр ви знаєте? Скільки чисел існує?
Ми прийшли до найвидатнішого відкриття математики - створення позиційної системи числення, а також до виникнення найголовнішої цифри в математиці - цифри нуль. Винайдений він був в Індії ще в V-VII ст. н. е. та інші цифри були винайдені також там. Під час жвавої торгівлі, яка була між Сходом і Заходом у ті часи, індійські цифри запозичили араби. А оскільки арабські країни мали вдаліше розташування для розвитку торгівлі з іншими країнами, то розповсюдження цифр по всьому світу пішло саме звідти, тому і назва цифр, якими ми користуємося, -арабські.
Повернемося до числа 0. З початкової школи ви вмієте записувати будь - яке число у вигляді суми розрядних доданків. Пригадаємо, як записати число 555 у вигляді суми розрядних доданків: 555=500+50+5, тобто у цьому числі 5 сотень, 5 десятків і 5 одиниць. Цьому ми завдячуємо числу 0, бо за допомогою нього ми можемо кожну цифру в числі записати на своєму місці, на своїй позиції. Тому систему числення і називають позиційною.
Подивіться, як незручно записувати числа в інших давніх системах числення.
Не можна обминути увагою число 12. Слов'янська назва цього числа - дюжина. Ще ваші прабабусі на ринку товар купували дюжинами, а не десятками.
Наступне число 13, яке в народі називають «чортовою дюжиною». З числом 13 пов'язано дуже багато прикмет і вірувань. І ось вам завдання додому: пригадайте самі, або запитайте в родичів, які забобони пов'язані з числом 13, вони знають.
Наш перший урок математики в 5 класі закінчується. Ми з вами, вивчаючи математику, будемо складати математичні казки, влаштовувати математичні турніри та грати в математичні КВК. Головне - запам'ятайте: математика найцікавіша і зовсім не важка наука для тих, хто хоче її знати.
Приклад 2. «Осінній бал» - 5 клас. Тема: «Кут та його елементи». Вчитель математики гімназії № 14 м. Луцьк - І.К. Панащук.
Мета: розширити відомості про геометричні фігури; ввести поняття кута і сформулювати його означення; ознайомити учнів із видами кутів; розвивати увагу, пам'ять, спостережливість; через застосування на уроці ігрових моментів активізувати мислення, викликати інтерес до вивчення предмета.
Тип уроку. Урок вивчення нового матеріалу.
ХІД УРОКУ
I. Організаційна частина.
Клас прикрашено осіннім кленовим листям, у кожного учня на парті лежать кленові листки, а також набори моделей гострого, прямого і тупого кутів.
ІІ. Актуалізація опорних знань
- Вступне слово вчителя.
Учитель. Усі ви любите математику і в майбутньому будете деякою мірою користуватися знаннями з цієї науки. Чи правда, що математики надзвичайно сухі, нудні і нецікаві люди? Звичайно, це неправда!
Усі ми любимо співати, танцювати, слухати музику. А ще ми вміємо фантазувати. Людській фантазії немає меж. Дякуючи їй, наприклад, у мультиплікаційних фільмах оживають предмети, іграшки, розмовляють птахи, квіти, тварини.
Сьогодні ми також трохи пофантазуємо: уявімо, що ожили відомі нам геометричні фігури, і ми їх запросили на наш «Осінній бал». Саме осінній, тому що надворі — осінь, яка і наш клас прикрасила різнобарв'ям своїх фарб.
Отже, бал розпочинається.
2. Представлення фігур.
Учні представляють відомі їм фігури: пряму, точку, промінь, відрізок, ламану, кути (розгорнутий, прямий, тупий і гострий).
Представляючи фігури, учні виходять на середину класу із прикріпленими до грудей аркушами, на яких зображено певні фігури.
Вони дають повну характеристику зображених фігур.
(Звучить вальс Є.Доги з художнього кінофільму «Мій лагідний і ніжний звір». Діти танцюють вальс «дружби».)
Учитель оголошує тему і мету уроку.
III. Вивчення нового матеріалу.
1. Означення кута.
За малюнком, виконаним на дошці, учні самостійно встановлюють, з яких фігур складається кут, дають його означення, називають елементи, звертають увагу на способи позначення кутів.
2. Практична робота.
Завдання 1. Накресліть на аркуші
паперу пряму АВ. Позначте на ній точку О. Дістали два промені зі спільним початком, які утворюють розгорнутий кут.
Учитель формулює означення розгорнутого кута.
Завдання 2. Перегніть аркуш паперу так, щоб лінія перегину пройшла через точку О — вершину розгорнутого кута. Через лінію перегину проведіть промінь OD. Утворилися два кути, кожен з яких дорівнює половині розгорнутого.
Учитель формулює означення прямого кута.
Завдання 3. Серед моделей кутів знайдіть рівні, виміряйте їх градусні міри.
Завдання 4. Накладіть модель гострого кута на модель прямого кута, а модель тупого кута — на модель прямого. Порівняйте ці кути. Зробіть відповідні висновки.
Учитель формулює означення гострого і тупого кутів.
Запитання до учнів.
1) Яка фігура називається кутом?
2) З яких елементів складається кут?
- Які є види кутів? Сформулюйте їх означення.
- Що можна сказати про тупий та гострий кути, порівнюючи їх із прямим кутом?
IV. Закріплення знань.
- Накресліть три різні кути, позначте їх вершини і сторони. Запишіть назву кожного з кутів двома способами.
- Серед накреслених на дошці кутів назвіть прямі, гострі й тупі. Зробіть відповідні записи.
- Чи правильні твердження?
А)Кутом називається фігура, яка складається з двох променів.
Б)Кут — це фігура, яку утворюють два промені зі спільним початком.
В)Розгорнутим кутом називається кут, утворений двома променями, що лежать на одній прямій.
Г) Розгорнутим кутом називається кут, у якого сторони — доповняльні промені.
Д)Тупим кутом називається кут, який більший від прямого.
Е)Тупим кутом називається кут, який більший від прямого, але менший від розгорнутого.
Якщо, відповідь позитивна, то учні піднімають руку з кленовими листками.
Розв'язування вправ.
1. Запишіть усі кути, зображені на малюнку. Чи є серед них гострі, тупі, прямі кути?
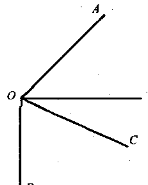
D
2. (Усно.) Визначте на око вид кутів, зображених на малюнку.
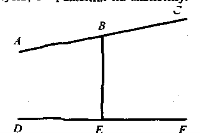
- З допомогою якого інструмента можна швидко і правильно накреслити прямий кут? (Транспортир)
- Накресліть гострий кут MON і тупий кут MOD. Побудуйте промінь (К так, щоб кут МОК був прямим.
- Додаткові вправи.
1. Розв'яжіть рівняння:
а) 347 + (х- 29) = 561;
б) 240 — (х - 35) = 72.
2. Назвіть кути, зображені на малюнку.
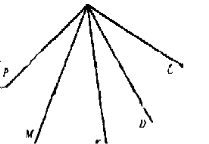
VI. Підсумок уроку.
VII. Завдання додому.
Вивчити п. 2.6, виконати вправи 153, 154, 208 г, д.
Приклад 3. Тема «Додавання і віднімання десяткових дробів» - урок-залік в 5-му класі. Тип уроку – узагальнення знань. Вчитель математики ЗОШ 1-2 ступенів № 268; м. Київ – Л.С. Боровська.
Мета: узагальнити і систематизувати відомості про десяткові дроби, зокрема про додавання і віднімання десяткових дробів; закріпити вміння і навички застосування цих дій до розв'язування задач; розвивати логічне мислення та уяву; виховувати культуру математичних записів, такі моральні якості, як уміння прийти на допомогу тим, хто знаходиться в біді, доброзичливість.
ХІД УРОКУ
I. Мотивація діяльності.
Вчитель. На уроці ми будемо узагальнювати і систематизувати знання, вміння та навички, які стосуються додавання і віднімання десяткових дробів.
Для цього здійснимо мандрівку в казку «Снігова королева».
Сподіваюся, ви добре знаєте головних героїв казки — Кая і Герду. Скажіть, що трапилося з Каєм? (Серце хлопчика перетворилося на лід. Його забрала у свій палац Снігова королева.)
А Герда вирішила відшукати Кая. Для цього, за правилами нашого уроку, їй потрібно розв'язати значну кількість задач. І ми їй у цьому допоможемо.
II. Перший етап мандрівки.
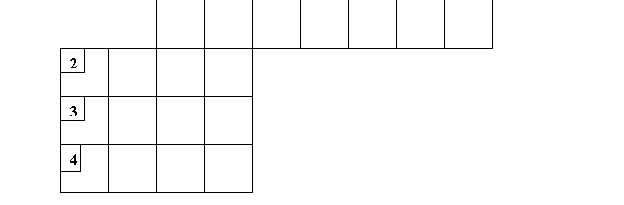
Вчитель. На своєму шляху Герда зустріла бабусю, якій вона дуже сподобалася, а тому бабуся вирішила залишити дівчинку в себе. Для цього вона завела Герду в будинок і замкнула двері на ключ. Щоб вибратися з будинку, дівчинці потрібно розв'язати чайнворд.
Допоможемо їй це зробити.
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
|
|
1 |
|
|||||
|
|
|
|
|
3 |
|||
|
5 |
|
|
|
|
|
4 |
|
Запитання чайнворду
1. Найменше натуральне число. (Один)
- Прийоми найменування та позначення чисел. (Нумерація.)
- Англійська одиниця довжини, яка приблизно дорівнює 91 см. (Ярд.)
- Компонент дії додавання. (Доданок.)
5.Прямокутник, у якого всі сторони рівні. (Квадрат.)
III. Другий етап мандрівки.
Вчитель. Впоравшись із завданням,
Герда вирушила далі. У дорозі вона зустріла галку, якій розповіла свою історію. Галка знала принца Кая і пообіцяла дівчинці влаштувати з ним зустріч, якщо Герда правильно прочитає числа: 0,1804; 1,804; 18,04; 180,4; 1804. Чи зумієте і ви це зробити? (Учні читають числа.)
А чим знаменний 1804 p.?
(Це рік заснування першої в Україні гімназії у місті Новгороді-Сіверському.)
IV. Третій етап мандрівки.
Вчитель. Дівчинка зустрілася з принцом, але це був не її Кай. Герда розплакалася, але принц її заспокоїв і сказав: «Якщо ти в порожні клітинки запропонованих прикладів запишеш такі цифри, щоб утворився правильний вираз, то отримаєш карету і вирушиш у дорогу».
Для цього Герді потрібно пригадати, як додаються та віднімаються десяткові дроби, визначити, яку дію слід виконати над числами і замість зірочок записати цифри.
Зробіть це і ви.
Приклади
41,5*3 5*,386
2*,37* 26,* 5*
*9,*94 *1,2*4
V. Історична довідка.
Сучасні знаки «+»і«—» стали загальновживаними, починаючи із XVII ст. Уперше ці знаки з'явилися в праці німецького математика Я.Відмана (1489 р. — І половина XVI ст.). Вважають, що спочатку знак «—» використовували для позначення недостачі, збитку в торгівлі, а знак «+» для позначення прибутку.
У різних народів знаки додавання і віднімання спочатку мали неоднакову форму. Так, у стародавніх єгиптян знак «+» нагадував зображення двох ніг, що рухаються вперед, а знак «—» був схожий на зображення двох ніг, що рухаються назад.
VI. Четвертий етап мандрівки.
Вчитель. Тільки-но Герда заїхала в темний ліс, як на неї, наче шуліки, налетіли розбійники. Маленька розбійниця пообіцяла відпустити її, якщо дівчинка порівняє числові вирази:
а) 13,2+І 8,04 і 48,36-17,04;
б) 61,57-14,64 і 15,3+ 31,72.
Порівняйте ці вирази і ви. (Учні роблять необхідні обчислення, формулюють правило порівняння десяткових дробів і розв'язують завдання.)
- П'ятий етап мандрівки.
- Учитель. Далі Герді допомагав подорожувати олень. Вони дісталися до
Лапландії та зупинилися в хатинці лапландки для відпочинку. Разом із ними відпочинемо і ми.
- Музична пауза.
(звучить мелодія скрипки)
- Шостий етап мандрівки.
Вчитель. Після відпочинку лапландка попросила Герду розв’язати такі рівняння:
а) 4,923 +Х+ 9,01 = 53,128;
б) 35,28 – 2,453 – У = 26,19.
Герда виконала її прохання і сказала, що коренями рівнянь будуть числа 39,195 та 6,638. Чи не помилилась вона?
(учні розв’язують рівняння, коментуючи свої дії та зіставляючи свої результати з результатами Герди.)
- Сьомий етап мандрівки
Виконавши завдання Герда та олень вирушили далі і натрапили на фінку, яка жила в тих самих місцях, що й Снігова королева. Жінка погодилася допомогти їм у пошуках палацу за умови, що вони розв’яжуть задачу.
Задача. Швидкість човна проти течії річки дорівнює 9,5 км. на годину, а швидкість течії – 1,6 км. на годину. Обчисліть швидкість човна в стоячій воді і за течією річки.
Вчитель: давайте разом з Гердою також розв’яжемо цю задачу. (учні розв’язують задачу)
Герда, як і ви, також правильно вирішила цю задачу і дійшла до паласу, в якому жив Кай. І в цьому, як ви і бачили, їй допомогли знання математики.
- Підсумок уроку.
- Домашнє завдання.
Приклад 4. Урок на всі дії з десятковими дробами «З Любов’ю до рідного краю» - 5 клас. І.С. Ступак, учитель математики, с. Грузьке Макарівського р-ну Київської обл.
Мета: формувати і закріпити вміння та навички розв'язувати вправи на всі дії з десятковими дробами; розвивати навички усної лічби; виховувати любов до рідного краю.
Обладнання: математичне лото, кросворд-розминка; картки-відповіді.
ХІД УРОКУ
І. Кросворд-розминка.
(На дошці написане завдання, які учні усно виконують у довільному порядку, а результат записують до кросворду
![]()
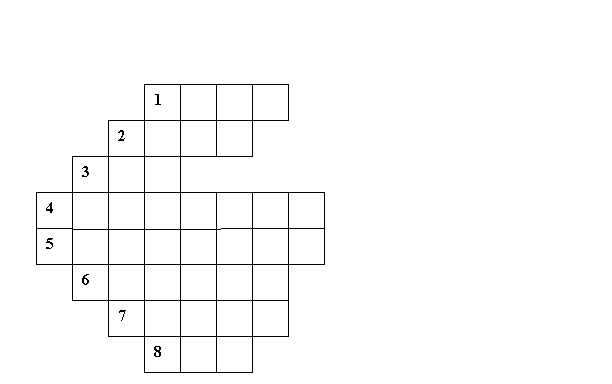
1.0,02 : 0,004. (П'ять.)
2.Яке число записують «у два поверхи»? (Дріб.)
3.1,25 х 80. (Сто.)
4.Властивість множення. (Сполучна.)
5.0,8 х 640 + 0,8 х 360. (Вісімсот.)
6.Компонент при діленні. (Частка.)
7.2,8 : 0,07. (Сорок.)
8.Як називається фігура, яка складається з двох променів, що виходить з однієї точки? (Кут.)
Учитель. Ключове слово кросворду — пролісок. Це найперші квіти, що розквітають в Україні навесні. Проліски із родини амарилісових і є провісниками весни. Вони квітнуть навіть тоді, коли на вулиці нуль градусів. Виявляється, що я цей час температура всередині квітки близько 8 градусів тепла. Квітка має таку будову, що її чашечка, немов маленьке дзеркальце, вбирає сонячне проміння. Пролісок здатний витримати до 10 градусів морозу.
ІІ Естафета.
Учитель. Чи знаєте ви, який найбільший пернатий птах у Європі? Дізнаймося про це, якщо знайдемо значення виразу.
(1,184 : 3,2 + 0,832 : 0,4) : 0,5 + 1,5.
Учні по черзі виконують біля дошки дії і шукають результат, який дістали, серед записаних на картках чисел. На протилежному боці карток написано літери.
0,37 2,08 4,9 2,45 6,4
н у и п ш
Після завершення роботи учням потрібно розставити результати в порядку спадання, повернути картки і прочитати слово «шипун».
Учитель. Найбільший пернатий птах в Україні, а також у Європі – лебідь – шипун. Довжина його тіла становить 180 см, важить він від 8 до 18 кг. У Польщі, кажуть, жив колись лебідь вагою 22,5 кг. Через таку вагу він не міг літати.
ІІІ. Розв’язування рівнянь.
Два учні біля дошки розв’язують рівняння.
- (х – 0,95) * 0,18 = 0,549.
Відповідь. 4.
- (8,5 – х) * 7,2 = 37,44.
Відповідь. 3,3.
- (41,9 – у) : 4,7 = 3,5.
Відповідь. 25,45.
- 0,2 * у * 62,5 – 3,25 = 4,25.
Відповідь. 0,6.
Після завершення роботи учням пропонують знайти розв’язки на запропонованих картках, розставити корені в порядку зростання та повернути картки, оскільки на їх зворотному боці написано літери.
4 3,3 25,45 0,6 0,92
о л з п о
Учитель. Найбільшою змією фауни України є полоз жовтобрюхий, довжина якого сягає 2 м. Це - таємнича та найагресивніша змія, хоч і зовсім не отруйна. Захищаючись, вона сичить і кидається передньою частиною тіла на відстань до 1 м, при цьому чіпляється своїми гострими й чисельними зубами за руку або обличчя кривдника. Зустрічається полоз рідко і лише в Степовій зоні України, населяючи берегові кручі. Основна здобич полозів – гризуни, хоча вони можуть полювати і на птахів.
ІV. Поле чудес.
На магнітній дошці записано завдання, але деякі числа запису закрито чистою карткою, на якій з іншого боку написано літери. Учні повинні дізнатися, яке число має стояти в кожному з рівнянь на порожніх місцях, повернути картки і прочитати слово «зубр».
5,8 : З = 58,
0,93 : 0,1 = У,
Б : 0,01 = 594,
0,057 : 0,0001 = Р.
Учитель. Найбільший звір фауни України – зубр, жива маса якого може перевищувати 1 т, висота досягає 2-3 м, а тривалість життя – до 27 років.
V. Математичне лото.
Учні виконують самостійну роботу парами.
Учні кожної пари дістають картки –завдання. Та картки –відповіді, на зворотному боці яких написано літери.
Картки – завдання.
0,12 : 2 + 4,1 * 2
0,308 : 0,14 + 1,08
7,224 : 0,301 – 18,6
120 – 7,2 : 0,6
19,56 : ( 3,2 + 4,95)
(19,85 + 4,65) : 5
(7,6 – 1,7 * 3,4) : 9,1
Картки – відповіді.
8,26 3,28 5,4 10 7,4 4,9 0,2
е ф л д і ь н
Учні після завершення роботи ставлять у відповідність картці – завданню картку – відповідь, розташовують відповідь у порядку спадання і читають відповідь «дельфін».
Учитель. Найбільший морський ссавець, який мешкає біля берегів України, це дельфін. Завдовжки він буває більшим за 3 м і важить у середньому від 119 кг до 150 кг. Живуть дельфіни невеликими групами і ведуть нічний спосіб життя. Живляться переважно рибою.
VІ. Підсумок гри.
VІІ. Домашнє завдання.
Скласти кросворд (числовий або текстово-числовий) з ключовим словом «масштаб».
Приклад 5. Тема уроку. Розв'язування вправ. По темі «Звичайні дроби». 5-клас. М.В. Ночевчук, учитель математики Червоногранітянської ЗОШ І –ІІ ступенів Володимир – Волинського р-ну Житомирської області. . Мета: навчити поєднувати математичну і нематематичну інформацію, удосконалювати знання учнів про звичайні дроби; розпинати логічне мислення, навички усної лічби, математичну мову; виховувати інтерес до нових знань і прагнення їх набувати.
ХІД УРОКУ
I. Перевірка домашнього завдання.
Повторення вивченого теоретичного матеріалу за питаннями 1—23 для самоперевірки за підручником: Возняк Г.М., Литвиненко Г.М., Маланюк М.П. Математика: Проб, підруч. для 5 кл. серед, шк. — К.: Освіта, 2000.
II. Розв'язування вправ.
1.Яку з букв А Б В Г Д Е слід вибрати?
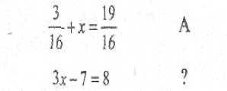
Розв'язання
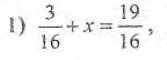
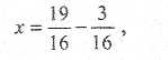
Потрібно розв'язати рівняння.
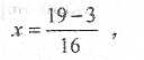
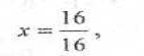
![]()
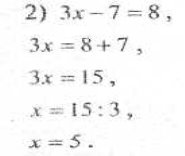
Замість знака «?» потрібно поставити букву, яка стоїть на п'ятому місці. Відповідь. Д.
2. Вставте пропущені числа, слова або малюнки.

Відповідь.
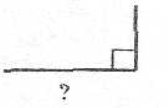
![]()
![]()
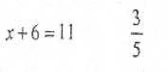
Відповідь. Розгорнутий кут.
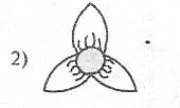
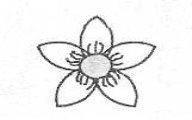
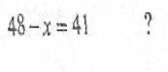
Розв'язання
Потрібно розв'язати рівняння:

Отже, чисельник шуканого дробу — кількість пелюсток квітки, а знаменник
- корінь даного рівняння.
Відповідь.
![]()
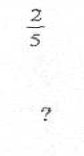

![]()
Відповідь.
(відношення зафарбованих кругів по всіх, які є).
3. Яке з даних чисел зайве:
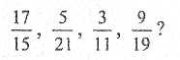
![]()
Відповідь.
( усі інші - правильні дроби).
4. Скільки потрібно зробити надрізів, щоб розрізати дерево на 8 частин?
Відповідь. 7.
5. Виконайте дії.
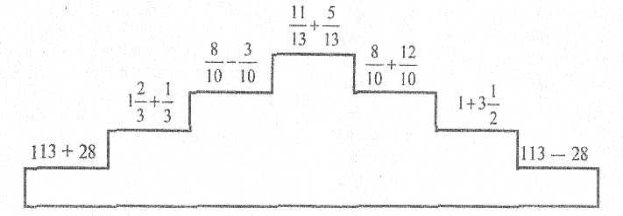
(Див. малюнок нижче ) Вправу виконують два учні біля дошки і перемагає той, хто швидше та правильно дійде до вершини.
6. Учитель читає завдання, а учні відповідають.
1) Якщо відповідь правильна, то піднімають руки вгору, а якщо неправильна — витягують вперед.
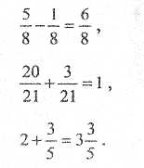
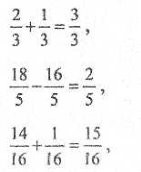
2) Якщо відповідь правильна, учні виконують поворот направо, а якщо неправильна — наліво.
Чисельник дробу показує, на скільки частин поділили величину, 1/2 години становить 30 хвилин, 3/5 більше за 4/5, 8/8 менше за 1.
7. Знайдіть невідоме число.

7/15 2/15 ?
Розв’язання
Звернемо увагу на перший рядок завдання. Кількість трикутників, зображених праворуч, дорівнює сумі трикутників, зображених ліворуч. Отже, шуканий результат одержимо, якщо додамо дроби:
Відповідь. 9/15.
8. Чи правильно ми говоримо?
Прийшов тато з міста, дає сину медівник та й каже: «На, Васильку, та поділися з Петриком по щирості». «А як діляться «по щирості»? — запитує Василько.«Отак, синку, — каже тато, — більшу половину даси Петрику, а меншу візьмеш собі». «То дайте Петрику медівник, нехай він поділить по щирості».Чи правильно тут вживається термін «половина»? Чи може бути одна половина більша, а друга — менша? (Учитель звертає увагу учнів на те, що слід говорити «більша частина» і «менша частина», оскільки половини мають бути однаковими. Адже дріб 1/2
Означає, що ціле (одиницю) поділили на дві рівні частини й узяли таку одну частину).
9. вставте пропущені числа , слова або малюнки.

Відповідь. Прямокутник.
2)
![]()
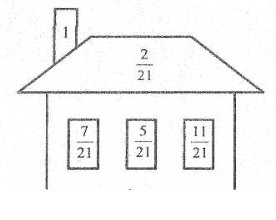
![]()

Розв’язання.
Розглянемо верхній будинок. Якщо від суми чисел, записаних на «вікнах», відняти число, записане на «даху», то буде 1, аналогічно і в другому будиночку відповіддю буде число 2.
10. переставте різними способами цифри так ,щоб дістати:
1) неправильний дріб із 109/110;
2) правильний дріб із 111/109.
Хто знайде більше способів?
Можна розповісти дітям кілька жартівливих історій.
Історія перша. На уроці вчителька перевіряла, як учні засвоїли дроби.
- Скільки буде, коли ми цілий пиріг поділимо на дві частини?
- Одна друга.
- А коли на чотири?
- Одна четверта.
- А на вісім частин?
- Одна восьма.
— А на шістнадцять?
«Крихти», — дружно відповіли діти.
Історія фуга. У мами дві доньки й один синок. Донечці — пиріжечок, другій — теж пиріжечок. А синочку? Ой, забула! Хай кожна сестриця дасть братику половинку! Так і зробили сестрички. То кому краще?
Учитель. Великий російський письменник Л.М.Толстой писав, що людину можна оцінювати дробом, знаменник якого становить те хороше, що вона думає про себе сама, а чисельник — те хороше, що думають про неї інші.
А як ви вважаєте? Чи правильно це? [З, с. 45]
Інсценівка «Вміло поділив»
(Виходять два учні.)
Перший учень. Ти знаєш, що в нашій сім'ї 5 осіб; батько, мати, я і дві сестрички?
Другий учень. Знаю. Крім того, знаю, що ти неввічливий. Потрібно було сестричок назвати першими, а не себе.
Перший учень. Добре. Слухай далі. Купила сьогодні мама 7 яблук і вирішила розділити їх порівну між нами. Спочатку вона одне яблуко розрізала на п'ять однакових частин, потім...
Другий учень. Досить. Я знаю, як ці яблука без розрізування на однакові частини можна між вами розділити.
Перший учень. 7 яблук на 5 осіб? Та ще й не різати?
Другий учень. Звичайно!
Перший учень. Цікаво, як же це зробити?!
Другий учень. Зварити компот!
III. історична довідка.
![]()

Найдавнішою пам'яткою Київської Русі з арифметики є твір про календар «Порадник, як людині пізнати числення літ», написаний слов'янською мовою в 1136 р. ученим монахом. Там використовуються такі дробові числа:
Хочете знати прізвище монаха? Тоді розв'яжіть кросворд і у виділеному стовпчику прочитаєте його.
Кросворд
1. Найменше натуральне число. (Один.)
![]()
2. Числа
(дроби)
3. Відстань між кінцями відрізка. (Довжина.)
- Наочне зображення різних відомостей і даних. (Діаграма.)
- Компонент дії додавання. (Доданок.)
- Одиниця вимірювання площ земельних ділянок. (Ар.)
- Одне з основних понять математики. (Число.)
- Відрізок, що сполучає дні точки кола і проходить через його центр.
(Діаметр.)
9.0, 1,2,3,4,5,6, 7, 8-це.... (Цифри.)
10. Найменше натуральне число, що закінчується нулем. (Десять.)
![]()
11. Як сказати одним словом (Половина)
12. Новгородцев.
![]()
![]()
![]()


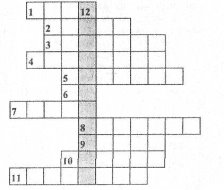
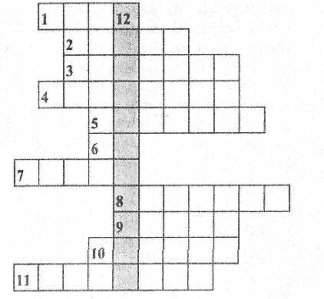
Правильно, це Кирило Новгородцев. З потреб практики спочатку виникло поняття дробу, що складався з кількох однакових частин одиниці. Тобто чисельник дробу 1, а знаменники різні.
В Єгипті дробами оперували ще 4000 років тому. Про це свідчать стародавні документи, які збереглися з тих часів. Проте загального способу позначення дробів, як це прийнято тепер, у стародавніх єгиптян не було.
У Греції та Єгипті довгий час користувалися дробами з чисельником 1. Інші народи навпаки користувалися дробами із сталим знаменником: вавилоняни — із знаменником 60, римляни — зі знаменником 12. Але вже грецький математик Герой Олександрійський (І ст. до н. е.) використовував дроби з будь-якими чисельником і знаменником.
У стародавній Русі дроби називали «частками», а згодом — «ламаними числами».
Окремі дроби мали спеціальні назви.
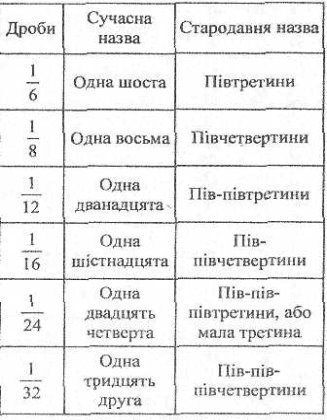
Записувати дроби з допомогою риски почали із XVI ст.
У давнину дії зі звичайними дробами викликали великі труднощі. Вавилоняни пояснювали це «втручанням злих духів». Англійський чернець Бєда (VІІ ст.), який був освіченою для свого часу людиною, писав: «У світі є багато речей, але немає нічого важчого, як чотири дії арифметики».
Тоді ж мабуть, і виникло німецьке прислів’я «потрапити в дроби», що означало опинитися в скрутному становищі.
А причина цих труднощів полягала в тому, що не було встановлено правил виконання дій з дробами, не було відповідної теорії.
Я думаю, що ви не потрапите в скрутне становище через дроби, оскільки вмієте виконувати дії з ними, і ваші знання з кожним роком поповнюватимуться.
ІV. Домашнє завдання.
Повторити пп. 4.1 – 4.4, виконати № 637, 638, 647. Придумати кросворд.
Приклад 6. Перший урок математики у 6-му класі, у формі змагання.
Вчитель математики СШ № 9 м. Фастів; Київської області – Л.О. Командирова
Мета уроку. Повторення навчального матеріалу 5-го класу на базовому рівні; розвиток пошукової пізнавальної активності учнів; розвиток логічного мислення; виявлення здібних до математики учнів; розвиток швидкості, кмітливості, наполегливості, просторового уявлення.
ХІД УРОКУ
1. Організаційні моменти
а) Поділ класу на команди (по рядах). Назви команд.
б) Умови конкурсу.
2. Розминка-кросворд
(Запитання задаються по черзі кожній команді, 1 запитання – 1 бал.)
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
6 |
|
|
|
|
|
|
|||||||||
|
|
7 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
9 |
|
|
|
|
|
|
|
|
||||||
По горизонталі:
- Частина прямого кута — (градус).
- Дріб, чисельник якого більший або дорівнює знаменнику — (неправильний).
- Прилад для вимірювання кутів — (транспортир).
- Знак пунктуації, який використовується в математиці — (кома).
- Трикутник, у якого дві сторони рівні — (рівнобедрений).
- Одна з основних геометричних фігур — (точка).
- Прямокутник, у якого всі сторони рівні — (квадрат).
- Рівність, що містить невідоме — (рівняння).
- Геометрична фігура, яку можна отримати, якщо продовжити відрізок в обидва кінці необмежено — (пряма).
Придумайте запитання до слова, яке вийшло у заштрихованих клітинках.
3. Цікаві задачі (за правильну відповідь по 1 балу).
- Кришка стола має чотири кути. Один з них відрізали. Скільки кутів стало у кришки? (П'ять).
- Оля трьома різними монетами заплатила за покупку, яка коштує 17 коп. Які це монети? (10 + 5 + 2 = 17).
- На столі лежало чотири яблука. Одне з них розрізали на дві частини. Скільки яблук на столі? (Чотири).
- Математична естафета (по 1 балу за приклад).
До дошки виходять по одному члену з кожної команди. Кожний з них отримує картку із завданнями. Розв'язавши перший приклад, учень передає картку як естафетну паличку другому члену команди, який розв'язує на дошці наступний приклад і т. д. Виправляти помилки попередніх учнів не можна. Перевіряє правильність розв'язання інша команда. За правильну перевірку — 1 бал.
Картки для команд
- 0,9×7
- 0,4×0,8
- 0,6 + 0,23
- 5 : 0,1
5) ![]()
- 0,3×8
- 0,4×0,6
- 0,5 + 0,41
- 6:0,6
1)1,4×2
2)0,3×0,7
3)0,2 + 0,36
4)66:0,6
5) ![]()
Учні записують у зошити розв'язання прикладів своєї команди.
5. Цікаві задачі (по 1 балу).
1. На скільки сума двох доданків більша від першого з них? (На число, яке дорівнює другому доданку).
- П'ять гномиків вишикувалися для гри. Білосніжна викликала третього гномика. "Скільки гномиків залишилося в шерензі? (Чотири).
- На день народження до дядечка Скруджа прийдуть семеро гостей. На скільки рівних частин він повинен розділити торт, щоб кожному було по шматочку? (На 8 частин).
6. Задачі від Незнайка. (Кожній команді по два приклади, по 1 балу за правильну відповідь.)
Незнайко придумав кілька прикладів на додавання і віднімання десяткових дробів, але конверт по дорозі промок під дощем і коми стерлися. Допоможіть виправити смішні рівності.
- 52 + 18 = 7
- 736 - 336 = 4
1) 3+108 = 408
2) 74 – 24= 5
1) 73 + 27= 10 2)57–4= 17
Запишіть приклади у зошити.
7. Геометричні задачі (по 2 бали).
1. Як скласти два трикутники з п'яти однакових паличок?
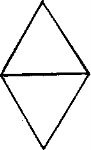
2. Проведіть в чотирикутнику відрізок так, щоб він поділив чотирикутник на трикутник і п'ятикутник.
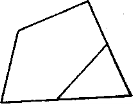
3. Замкнена ламана складається з чотирьох ланок. Які фігури вона може утворити?
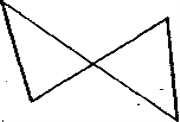
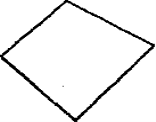
4. Завдання для всіх (4 бали). Незнайко накреслив три прямі, на кожній з них він поставив три точки. Всього Незнайко поставив 6 точок. Покажіть, як він це зробив.
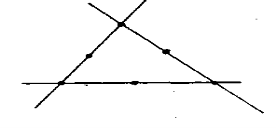
8. Алгебраїчні задачі (по 1 балу).
1. У наведених таблицях числа записано за певною закономірністю. Встановіть цю закономірність і знайдіть числа, які потрібно записати замість квадратиків.
|
4 |
2 |
6 |
|
1 |
8 |
9 |
|
7 |
3 |
□ |
1)
|
8 |
1 |
7 |
|
3 |
2 |
1 |
|
6 |
2 |
□ |
2)
|
4 |
2 |
2 |
|
10 |
5 |
2 |
|
27 |
3 |
□ |
3)
Відповіді:
1) 4 + 2 = 6
1 + 8 = 9
7 + 3 = 10
2) 8 – 1 = 7
3 – 2 = 1
6 – 2 = 4
3) 4 : 2 = 2
10 : 5 = 2
27 : 3 = 9
2. Дайте відповідь на запитання. Коли так буває?
а) 85 + х = 85 - х, ( х = 0)
б) 240 - х = х, ( х= 120)
в) x + 100 = 100 – х, ( х = 0)
9. Підсумки уроку. Нагородження переможців
Приклад 7. «Математичний бій» - 6-клас. Урок узагальнення знань. Тема: Додавання та віднімання звичайних дробів. Вчитель математики ЗОШ І-ІІІ ступенів №268, м Київ Л.С. Боровська.
Мета: систематизувати й узагальнити знання учнів з даної теми, розвивати інтерес до математики.
Обладнання: таблиці, картки. Програма математичного бою.
I. Математична розминка.
II. Бій між учасниками (змагання з розв'язування рівнянь).
- Математична естафета.
- Математичний футбол.
V. Домашнє завдання.
Підготовка до бою Учитель за тиждень повідомляє про проведення уроку-гри, допомагає у формуванні команд та журі, розробляє з учнями схему проведення гри, дає домашнє завдання, яке складається з нестандартних задач.
ХІД УРОКУ
Учитель повідомляє тему і мету уроку, оголошує програму математичного бою, нагадує правила гри, представляє журі, капітанів команд.
І. Математична розминка.
Кожна команда без підготовки обчислює значення десяти виразів. За кожну правильну відповідь команді нараховується 1 бал, а за неправильну - знімається 1 бал.
Завдання для 1-ї команди
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
Завдання для 2-ї команди
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
Завдання для 3-ї команди
1) ![]() 2)
2) ![]()
3) ![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
II. Бій між учасниками (змагання з розв'язування рівнянь).
Кожному учаснику пропонується картка з трьома рівняннями, які оцінюються 3 балами. Зважаючи на власні можливості, учень вибирає одне із завдань, розв'язує його і на звороті картки великими цифрами записує номер завдання та відповідь до нього. Журі оцінює правильність розв'язання рівнянь відповідною кількістю балів.
Картка 1
1) ![]()
2) ![]()
3) ![]()
Картка 2
1) ![]()
2) ![]()
3) ![]()
III. Математична естафета.
Кожна команда отримує дві картки із завданнями. Учасники команди почергово виконують дії. Останній учасник на звороті картки пише відповідь і віддає картку журі.
Картка 1
![]()
Картка 2
![]()
IV. Математичний футбол.
Команди отримують умови задач і розв'язують їх так, що наступну дію виконує інший член команди. Якщо команда помиляється, то задача передається для розв'язування іншій команді і так триває до того часу, поки задачу не буде розв'язано.
Задача для 1-ї команди Миколка, Сашко та Андрійко зібрали 46![]() кг макулатури. Миколка й Андрійко зібрали 34
кг макулатури. Миколка й Андрійко зібрали 34![]() кг, а Сашко й Андрійко 28
кг, а Сашко й Андрійко 28![]() кг. Скільки кілограмів макулатури зібрав кожний хлопчик?
кг. Скільки кілограмів макулатури зібрав кожний хлопчик?
Задача для 2-ї команди Площа першої кімнати дорівнює 17![]() м2 , другої — на 4
м2 , другої — на 4![]() м2 більша ніж першої, а третьої – на 2
м2 більша ніж першої, а третьої – на 2![]() м2 менша, ніж площі першої та другої разом. Яка площа трьох кімнат?
м2 менша, ніж площі першої та другої разом. Яка площа трьох кімнат?
Задача для 3-ї команди Маса цвяхів, що знаходяться в ящику дорівнює 67![]() кг. З цього ящика першого дня продали 20
кг. З цього ящика першого дня продали 20![]() кг цвяхів, а другого – на 3
кг цвяхів, а другого – на 3![]() кг більше, ніж першого. Скільки важить порожній ящик?
кг більше, ніж першого. Скільки важить порожній ящик?
V. Домашнє завдання.
За тиждень до гри вчитель пропонує учням розв'язати вдома шість цікавих задач,* Готові і дають журі для оцінювання, а одну із задач розв'язують на уроці.
1. Скоротіть дріб:
![]()
2. Знайдіть суму:
![]()
- Зібрали 100 кг грибів. Виявилося, що їх вологість становить 99 %. Коли гриби підсушили, то їх вологість знизилася на 98 %. Якою стала маса грибів після підсушування?
-
Відомо, що дріб
 нескоротний. Чи буде скоротним дріб
нескоротний. Чи буде скоротним дріб 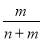 ?
?
- Доведіть, що n2 + п +1 не ділиться на 1974 ні для якого цілого п.
6.Ціну товару знизили на 10 %, а потім ще на 10 %. Чи став би він дешевшим, якби його ціну відразу знизили на 20 %?
VI. Підсумки математичного бою та уроку.
Приклад 8. Урок на тему: «Додатні і від’ємні числа» . Прямокутна система координат. «Навколосвітня регата» - дидактична гра для 6-го класу. З серії дидактичних ігор розроблених студентами фізико-математичного факультету Сумського державного педагогічного інституту ім. А.С.Макаренка С.Бурчак та Ю.Прокопенко під керівництвом доцента кафедри математики Л.Г.Чашечниковой та вчителя-методиста школи № 6 м. Суми Л.М. Трофименко Мета: Сприяти формуванню і розвитку інтелектуальних та творчих здібностей у процесі вивчення теми: Додатні і від’ємні числа. Прямокутна система координат.
(Рівень класу середній.)
ХІД ГРИ
Клас ділиться на 5 команд-кораблів, кожний має свого назву, наприклад, «Летючий Голландець», «Блискавичний», «Дуккан», «Наутілус», «Підкорювач штормів». У кожній команді вибирають капітана.
Гра проходить у 6 етапів:
Г. Старт.
II. Маршрут руху.
Ш. Рифи.
IV. Загублений острів.
V. Пірати.
VІ. Маяк (фініш).
Для збереження дисципліни в класі під час гри порушників карають відніманням набраних балів у їхньої команди.
Ведучий заготовляє таблицю, в яку вносяться результати етапів гри.
Таблиця результатів гри.
|
Команди/ етапи |
«Блискавич- ний» |
«Наутілус» |
…. |
«Летючий Голандець» |
|
Старт |
|
|
|
|
|
Маршрут руху |
|
|
|
|
|
Рифи |
|
|
|
|
|
Загублений острів |
|
|
|
|
|
Пірати |
|
|
|
|
|
Маяк (фініш0 |
|
|
|
|
|
Всього |
|
|
|
|
|
Місце |
|
|
|
|
І етап. СТАРТ
На цьому етапі потрібно привести екіпіровку корабля в повний порядок: розкласти все по своїх місцях, щоб нічого не заважало в подорожі.
Командам роздають картки. На виконання 2 хв.
Завдання. Записати в порядку зростання даний ряд чисел.
Картка 1: -8; -10; 0; 5; 1 ; -1; 3; -7; -199; 8; 15.
Картка 2: -1100; 1000; 500;-500; 0; 900; -800; 700; -470; -350.
Картка 3: 19: -І7; 13; 0; 27; -34; 16; -12; -11; 6; -1.
Картка 4: 12; -80; 1; -3; 0; 18; -23; 14; -17; -123.
Картка 5: 44; -52; 18; 0; -12; -6; -40; 50; -990; -9.
Результати. Команда, яка правильно першою виконала завдання, набирає 3 бали, друга — 1 бал, решта команд і ті, що припустили помилок, — 0 балів.
II етап. МАРШРУТ РУХУ
Не можна виходити в морс, не знаючи маршруту. Його (потрібно скласти, виконавши за 3 хв. наступне завдання.
Прикладом карток може бути така:
Побудувати в координатній площині точки: А (1; 1), В (4; 4), С (6; -3),
Д (-5; -4), Е (-3; 2) і сполучити їх відрізками (мал. 1)
Систему координат зображено на картці, учасники гри зображають задані точки. Кожна команда одержує окрему картку. Маршрут має бути схожим на п'ятикутник.
Результати: перша команда — 5 балів, друга — 3 бали, третя — 1 бал, інші, а також ті, що виконали завдання неправильно, — 0 балів.
III етап. РИФИ
У морі зустрічаються рифи, які заважають нормальному руху судна, і навіть, якщо ви правильно склали маршрут, рухались правильним курсом, шторм міг збити вас з курсу на рифи. Корпус вашого корабля пошкоджений і потребує негайного ремонту.
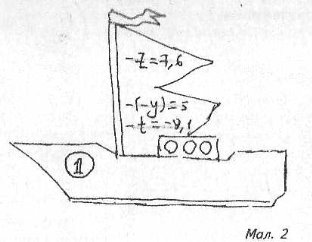
Завдання. Щоб зберегти корабель, потрібно за 3 хв. розв'язати рівняння, записані на заздалегідь заготовлених корабликах (див. мал. 2).
Результати: перша команда — 3 бали, друга — 1 бал, інші та з помилками — 0 балів.
IV етап. ЗАГУБЛЕНИЙ ОСТРІВ
На горизонті з'явився острів, якого на ваших картах немає.
Вам необхідно висадитися на цей острів, обійти його. На вашому шляху можуть з'явитися місцеві аборигени-людожери. Щоб захиститися від них і знайти назву острова, нам потрібно за 10 хв. розгадати кросворд. У сірих клітинках ви прочитаєте назву острова.
Результати: перша команда — 7 балів, друга — 5 балів, третя — 3 бали, четверта — 2 бали, п'ята — 1 бал, якщо завдання виконане неправильно, — 0 балів.
![]()
![]() 1 кросворд (мал. 3).
1 кросворд (мал. 3).
1. Координатна ...
- Число, яке не є ні додатним, ні від'ємним.
- Знак дії додавання.
-
Координатна пряма, на якій можна зобразити додатні, від'ємні числа і
нуль..
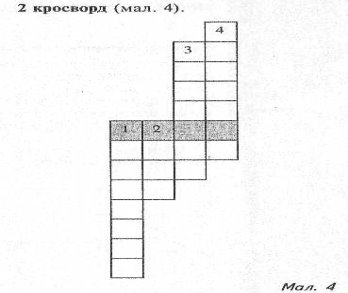
1. Друга координата точки.
2. 1/3 чи 5,67
3. Координатна ...
4.Число, яке знаходиться праворуч від нуля на координатній прямій.
3 кросворд (мал. 5).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
 Мал. 5
Мал. 5
- Одна з частин, па які ділять площину осі координат.
- Число, протилежне додатному.
- Перша координата точки.
-
Відстані, від початку відліку до точки, яка зображає число, або абсолютне
значення числа.
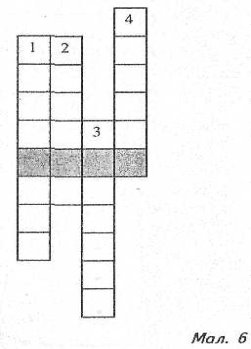
4 кросворд (мал. 6).
- Друга координата точки.
- Одиниця вимірювання температури.
- Координатна ...
- Одна з частин, на які ділять площину осі координат


![]()




![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() 5 кросворд (мал. 7)
5 кросворд (мал. 7)
Мал. 7
- Один з компонентів додавання.
- Якою буквою латинського алфавіту позначається вісь ординат?
- Координатна пряма, на якій можна зобразити додатні, від'ємні числа і нуль.
- Перша координата точки.
V етап. ПІРАТИ
Не встигли ви відпливти від острова, як на вас накинулися пірати: Сліпий П'ю, Чорний Корсар, Одноногий Сільвер, Володар Морів, пірати Братства Трьох Головорізів.
Щоб врятуватися від піратів, вам необхідно за 7 хв. знайти значення виразів, які місять модуль і записані на картках.
Мал. 8. Сліпий П'ю
Картки мають вигляд:
- ! – 10,5 + 4,7 ! + 3,1 : ! – 0,31!
- ! – 5,4 + 0,02 ! – 7,35 : ! – 0,735!
- ! – 7,31 ! * 3 - ! 5,37 – 10,85 !.
![]()
1. 13,2 : ! – 0,132 ! + 22,5 * ! -0,1 !.
![]()
2. ! 342 - ! 269 – 800 ! * 3 !.
3. ! -10,5 + 4,71 ! + 3,1 : ! – 0,31 !.
![]()

Мал. 11. Чорний Корсар
1. ! 8,12 – 10,03 ! : 3 – 3,05 ! – 3.
2. 15,3 - ! – 7,81 ! * 5 + ! – 13,2 !.
3. ! – 7,31 ! * 3 - ! 5,37 – 10,85 !.
- 13,2 : ! – 0, 132! + 2,25 : ! – 0,01!.
- ! – 5,4 + 0,02 ! – 7,35 : ! – 0,735!.
- 15,3 - ! – 7,81! * 5 + ! – 10,2 + 2,1!.
Результати: перша команда — 7 балів, друга — 5 балів, третя — 3 бали, четверта — 2 бали, п'ята — 1 бал. якщо завдання виконане неправильно, — 0 балів.
VI етап. МАЯК (фініш)
І ось, нарешті, на горизонті з'явився рідний маяк, вогник якого ледь-ледь світить в далечині.
Щоб прийти до свого порту, потрібно пройти останнє випробування: за 3 хв. перевірити, чи правильно поставлені знаки в прикладах. (Правильно «+», неправильно «—».)
Заготовлено 5 маяків, на яких написані приклади, правильність (неправильність) яких потрібно встановити, наприклад (мал. 13).
Приклади:
1. 12,2 < - 12,22,
- 3,8 < 3,80,
3. 6,25 < - 16,25,
4. – 1002 < - 10,02,
5. 32 = - 0,32.
Результати: перша команда -5 балів, друга -3 бали, третя -1 бал, інші та з помилками -0 балів.
У кінці гри підбиваються підсумки і нагороджуються переможці.
Приклад 9. Урок – залік по темі: «Множення звичайних дробів» у 6-му класі учитель-методист загальноосвітнього навчального закладу № 4, м. Рівне Г.Т.СЕМЕНЮК.
Мета: повторити вивчені правила з теми; сприяти розвитку уваги, кмітливості, логічного мислення та уяви; виховувати почуття доброти, бажання прийти на допомогу тим, хто її потребує, відповідальності за колектив.
Обладнання. Опорні таблиці, набори дробів і букв, кросворди, кольорова крейда.
ХІД УРОКУ
На магнітних дошках знаходяться таблиці з малюнками. На середніх — набір дробів і записані умови вправ, якими користуватимуться на уроці.
1. Вступне слово вчителя.
Сьогодні на уроці ми здійснимо подорож цікавою країною, назва якої Математика. Щоб урок був цікавим і ми встигли виконати більшу кількість завдань, поділимо клас на дві команди: «Юні математики» і «Дріб».
На уроці працюватиме журі: учитель математики, студені - практикант і учень випускного класу. Під час подорожі буде 7 зупинок.
2. Подорож.
І зупинка. Уважність
На дошці записано приклади з помилками в розв'язанні. Команди повинні їх виправити. Зліва записано завдання команди «Юні математики» (перша команда), а справа — команди «Дріб» (друга команда).
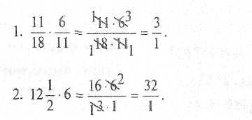
Друга команда
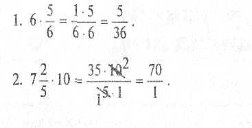
До дошки виходить по два учні від кожної команди і виправляють помилки, не переписуючи умови завдання. Відповіді.
Перша команда
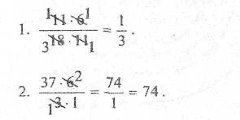
Друга команда
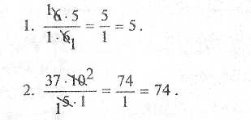
Наступні два учні детально пояснюють допущені помилки, використовуючи вивчений матеріал. Журі оцінює завдання двома балами, враховуючи швидкість і правильність виконання.
II зупинка. Дріб-товстун
Учитель. Ми побачили два дроби, а на очах у них — сльози. Як важко бути незграбним, а найстрашніше те, що з них усі кепкують. Можливо, їм потрібно займатися фізкультурою або дотримуватися дієти? Нічого не допомагає!
Чи зможете ви допомогти дробам?
![]()
Дроби:
До дошки запрошується два учні. Відповідь. Дроби потрібно скоротити:
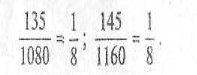
Журі оцінює це завдання двома балами.
ІІІ зупинка. Кмітливість
1. Конкурс капітанів команд. Із дробів, записаних на дошці для кожної команди, потрібно утворити всі можливі добутки, які дорівнювали б ½ (для команди «Юні математики») і 1/5 (для команди «Дріб»).
Перша команда
![]()
![]()
Дроби:
![]()
![]()
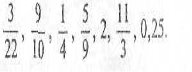
Відповіді:
![]()
![]()
![]()
![]()
![]()

Друга команда
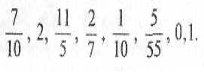
Дроби:
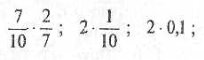
Відповіді:
![]()
Члени команд можуть допомагати своїм капітанам. Журі оцінює швидкість і правильність виконання завдання п'ятьма балами.
2. На магнітних дошках для кожної команди є таблиця. Чим потрібно замі нити знаки питання?
![]()
![]()
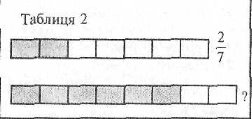
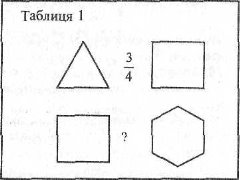
(таблиця 1),
![]()
![]()
(таблиця 2).
![]() До дошки запрошуються два учні.
До дошки запрошуються два учні.
IV зупинка. Математичне лото
![]()
Друга команда
![]()
На середній дошці підготовлено приклади для кожної команди.
До дошки виходять один за одним по чотири учні від кожної команди. Кожний учень виконує одну дію, враховуючи порядок виконання дій. Після виконання дії він підходить до стола, на якому лежать 8 прямокутників. На кожному з них є буква, а на протилежному боці — відповідь до однієї з дій.
Якщо всі дії виконано правильно, то команда «Юні математики» складе ЛАБІ, а команда «Дріб» — РИНТ. Разом буде ЛАБІРИНТ.
Журі оцінює завдання п'ятьма балами.
V зупинка. Казковий лабіринт
Учитель. Слово «лабіринт» грецького походження. У Стародавній Греції цим словом називали палац із багатьма кімнатами і складним їх сполученням, внаслідок чого було важко знайти вихід із нього. Два казкових героя — Зайчик і Песик — заблукали в лісі. Сильно втомившись, вони побачили хатинку на курячих ніжках. Наші герої зраділи і постукали у двері. Двері відчинила старенька бабуся. Вона пообіцяла допомогти їм, якщо вони знайдуть вихід із лабіринту.
На дошці вивішуються таблиці 3 і 4 і учні мають скласти вирази, значення яких дорівнює 1 ( команда «Юні математики») і 5 (команда «Дріб»).
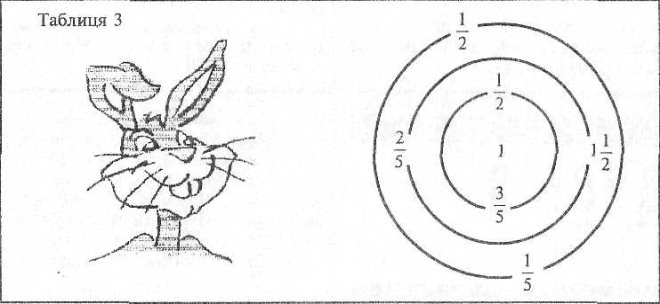
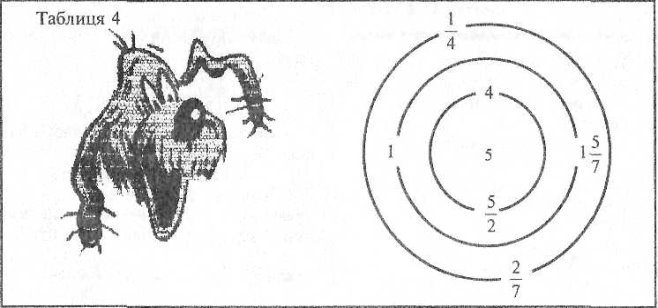
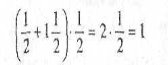
Відповіді:
Перша команда

або
Друга команда

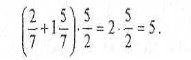
або
Учитель. Діти, ви молодці! Допомогли казковим героям вийти з лабіринту, адже самі вони з цим не впоралися б. Живіть і далі в країні милосердя і добра!
Журі оцінює це завдання п'ятьма балами.
VI зупинка. Відпочинок
Учитель. Що за подорож без відпочинку?! Послухайте математичну байку «Звичайні дроби»(читає вчитель української мови та літератури, запрошений на урок).
В огорожі круглих дужок
Сперечались дроби дуже.
Що ж у дужках круглих сталося?
Додавання не вдавалося!
Десять Третіх (дріб порядний)
Створить суму був би радий,
Але впертий Три Десятих
Не бажав із ним додатись.
І викрикував він гнівно:
«Ти як дріб мені не рівня!
Ти поглянь на моє личко:
Мій чисельник — невеличкий,
А знаменник зовсім інший,
За чисельник значно більший.
Я такий дріб, як і треба
А тепер поглянь на себе:
Десять третіх твій чисельник
Чомусь більший за знаменник,
Тому ти карикатурний,
Нестандартний, не фігурний,
Мабуть, ти як дріб не вдався,
Бо неправильно складався».
Не бажає Три Десятих
З Десять Третіх суму мати!
Через сварку числу Тридцять
Довелося зупиниться,
Біля дужок число стало
І, подумавши, сказало:
«Я на суму їх помножусь,
І це всім нам допоможе».
Тридцять діло своє знало —
Дробів два ліквідувало.
Дробів зовсім не лишилося,
Й сварка зразу ж припинилася.
Хоч ця байка і звичайна,
Є у ній мораль повчальна:
Хто закон шанує всюди,
Ліквідованим не буде!
Біля дошки два учні, по одному з кожної команди. Слухаючи байку, кожний учень повинен скласти вираз і знайти його значення.
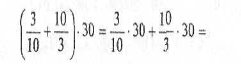
![]()
Журі оцінює завдання чотирма балами.
VII зупинка. Самостійна творчість
Учні підготували кросворди з теми «Звичайні дроби». Їх шість, усі знаходяться на дошках. Кожний учень отримує оцінку за кросворд і приносить додаткові бали своїй команді (1 бал за один кросворд).
3. Підсумок уроку.
Журі підраховує загальну кількість балів кожної команди і визначає переможців.
4. Домашнє завдання.
Задача: потрібно розділити 5 однакових яблук порівну між вісьмома хлопчиками. Як це зробити з найменшою кількістю розрізів?
Приклад 10. Тема «Дії з десятковими дробами» (Щасливий випадок - 6-й клас)
Вчитель математики й інформатики Колегіуму мистецтв; с. Опішне, Заньковецького району; Полтавської області - Л.М.Сиволга
Мета: удосконалити навички дій з десятковими дробами під час розв'язування задач; розвивати логічне мислення, вміння аналізувати, порівнювати, робити висновки; виховувати самостійність, наполегливість, культуру математичних міркувань, взаємоповагу.
Хід уроку
І. Організаційний момент.
Учитель. Добрий день, дорогі учасники гри! Сьогодні ви присутні на незвичайному уроці, який відбуватиметься у вигляді гри «Щасливий випадок». (Клас поділяється на дві команди, кожна з яких вибирає капітана і назву.)
Хід Гри
І гейм
«Далі, далі...»
Запитання для першої команди
- Як називається дріб, записаний з допомогою коми?
- Назвіть число, більше за 2,5 і менше за 2,6.
- Назвіть дії з десятковими дробами, під час яких числа записують так, щоб цифри однойменних розрядів були в одному вертикальному стовпчику.
- Як називається властивість, яка дає змогу переставляти місцями доданки?
5. Під час множення десяткового дробу на які числа слід лише перенести кому вліво на відповідну кількість десяткових знаків?
- Під час ділення десяткового дробу на які числа слід лише перенести кому вправо на відповідну кількість десяткових знаків?
- Чому дорівнює округлене до десятих значення числа 18,46?
- Якщо сумою двох чисел є число 8,6 і один з доданків дорівнює 6,2, то чому дорівнює другий доданок?
- Якщо один із двох множників дорівнює 5,6, а їх добуток 0,56, то чому дорівнює другий множник?
- Якщо ділене має п'ять десяткових знаків, а частка — два, то скільки знаків може мати дільник?
- Під час якої дії в обох числах кома переноситься на стільки десяткових знаків, щоб одне з них стало натуральним числом?
Запитання для другої команди
- Як називається дріб, записаний з допомогою риски?
- Назвіть дію з десятковими дробами, під час якої числа слід записувати одне під одним, не звертаючи уваги на коми.
- Назвіть операцію, під час якої всі числа додаються, і результат ділиться на їх кількість.
- Під час множення десяткового дробу на яке число слід лише перенести кому вправо на відповідну кількість десяткових знаків?
- Під час ділення десяткового дробу на яке число слід лише перенести кому вліво на відповідну кількість десяткових знаків?
- Як називається властивість, яка дає можливість переставляти місцями множники?
- Назвіть число, більше за 4,6 і менше за 4,7.
- Чому дорівнює округлене до десятих значення числа 15,73?
- Якщо сума двох чисел дорівнює 7,5 і один із доданків 3,2, то чому дорівнює другий доданок?
10. Якщо один із двох множників дорівнює 6,7, а їх добуток 67, то чому дорівнює другий множник?
11. Якщо ділене має три десяткових знаки, а частка — п'ять знаків, то скільки знаків може мати дільник?
II гейм «Ти — мені, я — тобі»
Команди-суперниці ставлять одна одній раніше підготовлені три запитання з даної теми.
3 гейм «Заморочки з бочки»
Учням пропонується відгадати загадки.
1. Щоб записувати числа
Чітко, правильно і стисло,
Щоб ці числа прочитати,
Точно все підрахувати,
Розгадати шифри,
Нам потрібні.... (цифри)
2. Чисел натуральних в світі є
багато, З них число найбільше не можна
назвати. Найменше ж знати всім
годиться, І це, звичайно, .... (одиниця)
3. На число це, знайте діти,
Заборонено ділити.
Проте множити — чудово,
Зразу відповідь готова.
Не роби собі проблем, Обережно будь з ...! (нулем)
4. Їх в підручнику багато,
Кожну треба розв'язати.
І не будьте ви ледачі
та розв'язуйте ... . (задачі)
5. По ній довго можна йти,
Кінця-краю не знайти.
І початку теж нема,
Бо ця лінія — ... . (пряма)
6. Щоб довжини виміряти,
Інструмент цей треба мати.
Як будуємо пряму —
Цей же прилад я візьму.
Вийде не пряма, а змійка,
Як загубиться... . (лінійка)
- В навчанні нам допомагає,
Про числа він розповідає,
Відрізки, формули, кути...
Його нам треба берегти.
Повинен знати кожний учень:
Наш друг і помічник — ... . (підручник)
IV гейм «Математична естафета»
Учні почергово виконують завдання естафети. Значення кожного попереднього виразу використовується для складання наступного.
Завдання для першої команди
24,5 : 10 = а,
а : 0,5 = б,
б • 10 = в,
в : 0,7 = г,
г • 0,01 = ґ,
ґ + 1,86 = д,
д : 1,6 = є,
є — 1,2 = є,
є + 5,6 = ж,
ж : 6 = з.
(Значення останнього виразу дорівнює 1.)
Завдання для другої команди
1,38 • 10 = а,
а : 0,2 = б,
б : 10 = в,
в - 3,5 = г,
г • 0,1 = ґ,
ґ : 0,2 = д,
д + 6,1 = є,
є : 0,06 = є,
є • 0,01 = ж,
ж : 1,3 = з.
(Значення останнього виразу дорівнює 1.)
III. Підбиття підсумків гри.
Визначаються команда-переможниця та активні гравці, які й нагороджуються призами.


про публікацію авторської розробки
Додати розробку
