Задачі на рух

       Задача 1.  По один бік шосейної дороги,  на однаковій відстані від шосе стоять два села А і В. З одного з сіл виїжджає посильний, який бере пошту у листоноші, що їде автомобілем по шосе. Посильний спершу завозить пошту сусідам, а потім собі. Визначити, в якому місці шосе повинен чекати посильний, щоб шлях, який йому доведеться проїхати, був найкоротшим.

Розв’язання

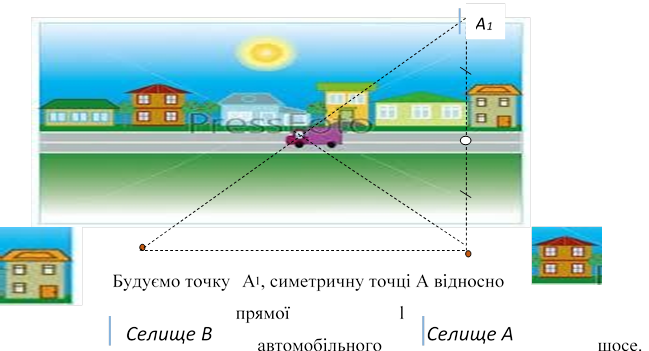
Оскільки найкоротша відстань – це пряма, то посильний має їхати в напрямку ВА₁. Пряма  ВА₁  перетинається  з прямою l в точці С.

 Задача 2. Людина стоїть на відстані 6м від річки. На відстані 24 м від річки

горить багаття. Відстань між перпендикулярами, які сполучають берег річки з людиною і багаттям, дорівнює 30м. Людина біжить зі  швидкістю 5 м/с до річки, зачерпує відро води, потім біжить до багаття  і заливає його. Який мінімальний час їй потрібен для

цього. Якщо на зачерпування води їй потрібно 5с?  Розв’язання

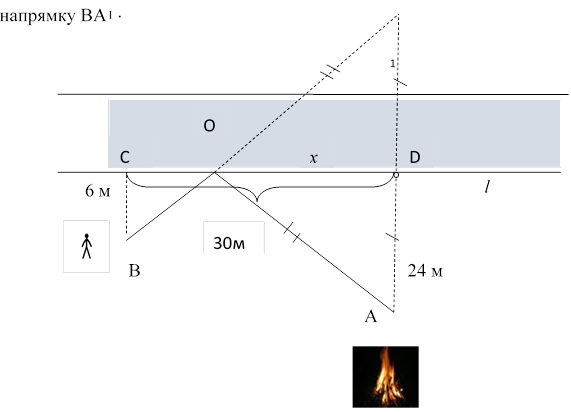
Будуємо точку А1, симетричну точці А відносно берега річки( прямої l).

Щоб затратити найменший час для гасіння багаття людина має бігти в

 А

 

Річка

        

Використовуючи подібність трикутників ВСО і АDО, знайдемо ОD:

.

Тоді  ВО² = 6² +6² = 72м²;  ОА² = 24²+24²=1152 м^2., тоді ВО ≈8,5 м, ОА ≈34м.

Найкоротша відстань, яку пробігатиме людина S≈42,5м, тоді мінімальний час t = 42,5м : 5м/с = 8,5с.

 Задача 3^. Не дочекавшись тролейбуса  на зупинці А, хлопчик пішов до

наступної зупинки В. Пройшовши 1/3 шляху, він озирнувся і помітив, що до зупинки А наближається тролейбус . Якщо хлопчик побіжить до зупинки А або до зупинки В, то в обох випадках він встигне сісти на

тролейбус. З якою швидкістю повинен бігти хлопчик, коли відомо, що тролейбус рухається зі швидкістю 30 км/год?

Розв’язання

Якщо хлопчик побіжить до зупинки А, то він прибіжить туди одночасно з приходом тролейбусу. Через те, що хлопчик від зупинки В був удвічі далі, ніж від А то, коли він побіжить до В і пробіжить півшляху, тролейбус саме підійде до зупинки А. Після цього тролейбус і хлопчик прибудуть на зупинку В, але тролейбус проходить при цьому шлях, вдвічі довший, ніж пробігає хлопчик.

Отже, швидкість хлопчика дорівнює 10 км/год.

 Задача 4^. Двоє спортсменів бігають на стадіоні в однаковому напрямку.

Перший витрачає на шлях 6 хвилин, а другий - 4 хвилини. Другий почав свій рух

на три хвилини пізніше першого, з того ж місця, що й перший. Через скільки хвилин після початку руху першого спортсмена його наздожене другий?

Розв’язання

                                                                                           Нехай довжина кола l. Тоді за одну хвилину

перший спортсмен пробіжить відстань рівну 1/6 l, а другий 1/4 l. За 1 хвилину другий наближається до першого на відстань 1/4 l -1/6 l =1/12 l. Оскільки другий спортсмен почав свій рух на три хвилини пізніше, перший за цей час проїхав 3∙ 1/6 l = 1/2 l. Щоб наздогнати першого спортсмена другому потрібно часу: t=1/2 l:1/12 l =6 (хв). Тому через 9 хвилин  перший спортсмен наздожене другого. Задача 5. В сиву давнину послали  гінця  із Києва до Москви, і веліли йому

щодня проходити по 40 верст. Наступного дня вслід йому послали другого гінця, і наказали  йому проходити в день 45 верст. На який день другий гінець наздожене першого?

Розв’язання

За  день перший гінець пройде в напрямку на Москву 40 верст, і значить  до початку другого дня буде випереджати другого гінця на 40 верст. Кожного наступного дня перший

гінець буде проходити по 40 верст, другий по 45, а відстань між ними буде скорочуватися на 5 верст. Ця відстань за 8 днів скоротиться на 40 верст. Отже, другий гінець дожене першого під кінець восьмого дня свого переходу.

Задача 6^. Двоє вартових вийшли одночасно з наглядом один за одним із

одного міста, тримаючи шлях навколо міста. Один із них йде по 4 версти за

годину, а другий – по 3¹ версти за годину. Шлях 3

навколо міста становить 15 верст. Через який час вони зустрінуться і скільки разів кожен із них обійде місто?

Розв’язання

За перший день другий вартовий відстане від першого на 4 - версти, за

2 другу годину на  версти, за третю годину ще на версти і т.д. Вартові зійдуться 3

знову, коли відставання дорівнюватиме довжині шляху навколо міста, тобто дорівнюватиме 15 верстам. На такі мандри потрібно  = 2,5 години.

Перший вартовий пройде за цей час 4 ^. 2,5 =90 верст, і обійде 90: 15 =6 разів навколо міста. Другий вартовий пройде на 15 верст менше, і, значить, зробить на один обхід менше.

Задача 7. Один воїн вийшов з міста і проходив 12 верст за день, а другий вийшов одночасно з першим і йшов так: в перший день пройшов 1 версту, другого дня – 2 версти, третього – 3 версти і так щодня прибавляв щодня по одній версті, доки не наслідує першого. Через скільки днів другий воїн наздожене першого?

Розв’язання

За перший день другий воїн відстане на 12-1=11 верст , за другий ще на   12 - 2 = 10 верст, за третій ще на 12 - 3 = 9 верст і так далі. На 12 день відставання складе (11+10+9+…+2+1+0) верст. 

А потім відставання між ними стане скорочуватися. На 13-ий день на      1312=1 версту, на 14-ий день ще на 14-12=2 версти, а на 15-ий день ще на 15-12=3 версти, і на кінець на 23-ій день на 23-12=11 верст. На 23-ій день відстань між ними скоротиться на (1+2+3+…+10+11) верст. Це означає,що через 23 дні другий воєн наздожене першого.

Задача 8. Мандрівник  запитав іншого мандрівника, що йшов у нього попереду: «Чи далеко до села, що у нас попереду?» Другий мандрівник відповів: «Відстань від того села, від якого ти йдеш, дорівнює третій частині всієї відстані між селами, а якщо пройдеш ще 2 версти, тоді будеш рівно посередині між селами». Скільки верст ще залишилось пройти мандрівнику?

Розв’язання

До половини відстані між селами першому мандрівнику потрібно йти         2 версти, і це становить   частина всієї відстані між селами. Тому відстань між селами дорівнює 2 : 12 верст, до моменту зустрічі перший мандрівник пройшов  версти і залишилось йому йти ще 8 верст.

Експериментальні задачі

Задача 1. Дослідити характер руху повітряної бульбашки в скляній трубці, наповненій водою.

Обладнання: скляна трубка завдовжки 1—1,5 м, діаметром 1см, запаяна         з одного кінця, корок, посудина з водою, масштабна  лінійка, гумові кільця —2 шт., секундомір.

Розв’язання

 Наповнимо скляну трубку водою, залишивши в ній повітряний стовпчик. Щільно закриємо трубку корком і надінемо на неї гумові кільця на деякій відстані одне від одного. Встановимо трубку вертикально бульбашкою вниз. За допомогою секундоміра визначимо протягом якого бульбашка пройде відстань.

Обчислимо модуль швидкості v .

Повторимо експеримент з різними відстанями s₁, s₂, s₃, s₄,…  

і засікаючи щоразу час t₁, t₂, t₃, t₄,…  знайдемо модулі швидкості для кожного випадку. Числові значення швидкостей рівні. Отже, рух повітряної бульбашки в трубці з водою рівномірний.

Задача 2. Дощові краплі падають вертикально. Яким здається рух крапель, якщо дивитися на них з вікна рухомого потягу? Як за слідок краплі на вікні визначити швидкість потягу?

Розв’язання

Рух дощових крапель здаватиметься косим, відхиленим у бік, протилежний руху поїзда.

 Задача 3. Приблизно визначте довжину свого кроку. Перевірте точність своєї оцінки за допомогою рулетки. Визначте середнє значення довжини кроку.

Скориставшись годинником, визначте середню швидкість свого руху по дорозі.

Побудуйте графік залежності швидкості від часу.

 Задача 4.  Виїхавши, рано-вранці,  за  межі  міста,  водій  автомобіля  вирішив зробити  зупинку рівно  за  годину  від  часу  виїзду.  Як  йому  здійснити свій  намір,  якщо годинник  і мобільний телефон він  забув  вдома, а радіоприймач в авто не працює?

Задачі для самостійного розв'язування

1.        Із пункту С, по колу в протилежних напрямках, виїжджають два велосипедиста. Перший проїжджає  коло за 12 хв, через 5 хвилин із пункту С виїжджає другий  велосипедист і проїжджає коло за 10 хвилин. Коли велосипедисти зустрінуться? 

2.        Мотоцикліст  проїхав  відстань  між  двома  пунктами  з швидкістю  40

км                                                                                             км

 . Потім,  збільшивши  швидкість  до  80 ,  проїхав  відстань,  удвічі  год          год меншу. Визначити  середню  швидкість за  весь  час  руху.

3.        З  одного  міста  в  друге  вийшов  пішохід.  Коли  він пройшов відстань  S₁=27 км,  слідом  за  ним  виїхав  автомобіль, швидкість  якого  у  10  разів  більша.  До  другого  міста  вони  прибули одночасно.  Яка відстань  між  містами ?

4.        Першу годину автомобіліст їхав зі швидкістю 50 км/год і розрахував, що якщо він і далі буде їхати з тією ж швидкістю, то запізниться в місто на півгодини. Він збільшив швидкість на 20% і прибув до міста вчасно. Який шлях проїхав автомобіліст і скільки часу він перебував у дорозі?

5.        Велосипедист проїхав 5/7 усього шляху і ще 40 км. Проте йому залишилося проїхати 0,75 усього шляху без 118 км. Який шлях повинен проїхати велосипедист?

6.        Відстань між станціями А і В пасажирський поїзд проходить на 45 хв швидше, ніж товарний. Визначити відстань між цими станціями, якщо відомо, що швидкість руху пасажирського поїзда дорівнює 48 км/год, а товарного - 36 км/год. Першу годину туристи йшли на станцію зі швидкістю 3,5 км/год.  Після цього вони розрахували, що якщо і далі будуть йти з тією ж швидкістю, то прийдуть на годину пізніше назначеного терміну. Збільшивши швидкість на 1,5 км/год, туристи прибули на станцію на 30 хв раніше назначеного терміну. Який шлях пройшли туристи?

7.        Відстань між двома селищами дорівнює 9 км. Дорога має підйом, рівнинну ділянку і спуск. Швидкість пішохода на підйомі дорівнює 4 км/год, на рівнинній ділянці 5 км/год, а на спуску 6 км/год. Скільки кілометрів становить рівнинна ділянка, якщо пішохід проходить відстань від одного селища до іншого і назад за 3 год 41 хв?