Збірник олімпіадних задач з математики для учнів 6 класу. Частина 3. Рівняння і невідомі

Рівняння і невідомі

1. Розв’яжіть рівняння: .

2. Розв’яжи рівняння:

а) ;

б) .

3. Який з виразів може мати найменше (найбільше) значення? При яких значеннях воно його досягає? Визначити найменше (найбільше) значення кожного з виразів:

а) ;

б) ;

в) .

4. Який з виразів може мати найменше (найбільше) значення? При яких значеннях воно його досягає? Визначити найменше (найбільше) значення кожного з виразів:

а) ;

б) ;

в) .

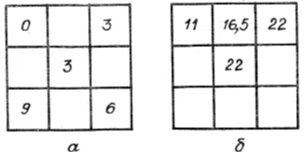
5. Заповнити пусті клітинки квадрату, зображеного на рисунку, використовуючи закономірність.

6. Розв’язати рівняння: .

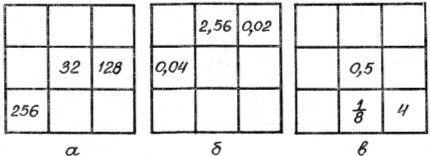
7. Заповнити порожні клітинки квадрату, зображеного на рисунку, числами так, щоб добуток всіх чисел кожної вертикалі, горизонталі і діагоналі складав для першого квадрату , для другого , для третього . Числа, записані в квадраті, розмістити в порядку зростання їх величини. Встановити закономірність чисел, записаних в порядку зростання їх величини.

8. Довести, що значення виразу не залежить від .

9. Який з виразів може мати найменше (найбільше) значення? При яких значеннях воно його досягає? Визначити найменше (найбільше) значення кожного з виразів:

а) ;

б) ;

в) .

10. При яких натуральних значеннях значення виразу:

а) буде кратне числу ;

б) буде кратне числу ?

11. Чи можна вказати найбільше і найменше значення виразу:

а) ;

б) ?

Якщо відповідь позитивна, вкажіть це значення і значення , при якому вираз його набуває.

12. Чи можна вказати найбільше і найменше значення виразу:

а) ;

б) ?

Якщо відповідь позитивна, вкажіть це значення і значення , при якому вираз його набуває.

13. Якого найменшого значення і при якому значенні може набути вираз:

а) ;

б) ?

14. Якого найбільшого значення і при якому значенні може набути вираз:

а) ;

б) ?

15. При яких значеннях не має коренів рівняння:

а) ;

б) ?

16. Знайдіть усі цілі значення , при яких є цілим числом корінь рівняння:

а) ;

б) .

17. Знайдіть усі цілі значення , при яких є натуральним числом корінь рівняння:

а) ;

б) .