Збірник олімпіадних задач з математики для учнів 6 класу. Частина 4. Задачі геометричного змісту за готовими рисунками

Задачі геометричного змісту за готовими рисунками

1. На рисунку м, м і м. Обчисли периметр фігури.

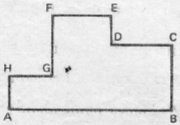
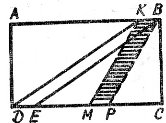
2. Через поле, яке має форму прямокутника , зображеного на рисунку, повинна пройти залізнична дорога. Відомо, що довжина поля м, ширина – м, м. Обчислити площу, яку буде займати залізнична дорога. Яка дорога буде мати більшу площу: чи ?

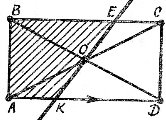
3. Прямокутник , зображений на рисунку, перетинає пряма , яка проходить через точку (точку перетину діагоналей і , ). Пряма повертається навколо точки (переміщуючи точку від до ). Визначити, чи змінюється при цьому і як саме площа заштрихованої фігури?

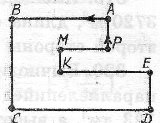
4. Гра на місцевості проходила за маршрутом , зображеним на рисунку. Старт і фініш були в точці . Обчислити довжину маршруту, по якому проходила гра, якщо км, км і м.

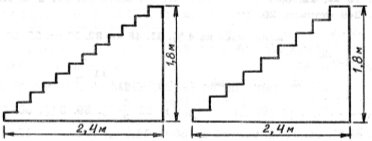
5. Двоє сходів, що мають однакову висоту м і основу м, накриті палацовими доріжками так, як показано на рисунку. Чи однакова довжина цих доріжок, якщо одні сходи мають , а інші – східців? Чи можна за цими даними обчислити довжину палацової доріжки?

6. На торті кондитер розмістив кремових трояндочок так, як показано на рисунку. Як трьома прямолінійними розрізами поділити торт на порцій, на кожній з яких була б одна трояндочка?

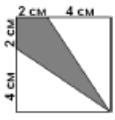
7. Обчисліть площу заштрихованої фігури, зображеної на рисунку (розмір наведено в сантиметрах).

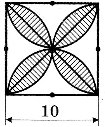
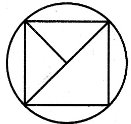
8. Усі вершини квадрата, зображеного на рисунку, діагональ якого дорівнює см, лежать на колі. Обчисліть площу квадрата, не вимірюючи його сторони. На скільки площа квадрата менша від площі круга?

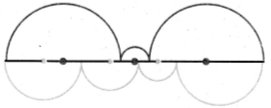
9. Доведіть, що сума довжин червоних дуг, зображених на рисунку, дорівнює сумі довжин зелених дуг.

10. Доведіть, що сума площ зафарбованих серпиків, зображених на рисунку, дорівнює площі прямокутника.

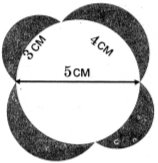
11. Два квадрати зі стороною см мають спільний центр, зображений на рисунку. Доведіть, що площа їх спільної частини більша за .

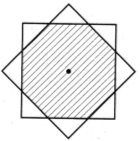
12. На рисунку показано старовинний спосіб обчислення площі круга. Спробуйте пояснити, чому добуток приблизно дорівнює площі круга.

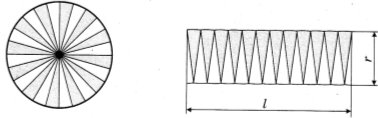
13. На рисунку зображено план ділянки. Чому дорівнює площа цієї ділянки, якщо масштаб цього плану складає ?

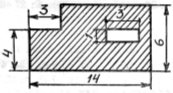
14. Обчислити площу затемненої частини квадрата.