Збірник задач з математики для підготовки учнів 9 класів до виконання четвертої частини державної підсумкової атестації
Даний посібник, який за своїм форматом є збірником задач, покликаний забезпечити дидактичним матеріалом учнів 9 класів на уроках математики під час розв'язування задач з математики підвищеного рівня складності, які містяться, у завданнях для державної підсумкової атестації та є у програмі для зовнішнього незалежного оцінювання школярів. Бажаним є використання цього видання для факультативних курсів за вибором вчителями математики у загальноосвітніх навчальних закладах. Основною метою даного посібника автор бачить у сприянні якісної підготовки здібних учнів до участі у предметних олімпіадах, конкурсах та при підготовці робіт слухачами Малої академії наук України.


![]()
Міністерство освіти і науки, молоді та спорту України
Відділ освіти виконавчого комітету Роменської міської ради Сумської області
Збірник задач з математики для підготовки учнів 9 класів
до виконання четвертої частини державної підсумкової атестації
Упорядник: учитель математики
Запека Андрій Юрійович
Посібник є дидактичним матеріалом з математики для учнів 9 класів як загальноосвітніх шкіл, так і шкіл з фізико-математичним профілем. Він містить 600 задач, що відповідають програмі з математики для загальноосвітніх навчальних закладів. Посібник призначений для підготовки учнів 9 класів до якісного виконання четвертої частини державної підсумкової атестації, класної та факультативної роботи на уроках математики, математичних гуртках і секціях, для підготовки до предметної олімпіади, роботі в Малій академії наук, його можна використовувати для роботи в класі і вдома.
Для учнів середніх та спеціалізованих шкіл, гімназій, ліцеїв.
Схвалено на засіданні методичної ради
учителів фізико-математичного профілю
Роменської спеціалізованої загальноосвітньої школи I – III ступенів № 2
ім. акад. А. Ф. Йоффе м. Ромни Сумської області
Ромни – 2018


Посібник присвячується випускниці СЗОШ № 2
ім. акад. А. Ф. Йоффе м. Ромни Сумської області
Бабій Катерині
в знак подяки за проявлені нею здібності
під час вивчення математики в школі, участі та
перемогам у Всеукраїнських учнівських олімпіадах
з математики, турнірів та конкурсів з предмету.
Зміст
|
Передмова |
5 |
|
Зразок виконання завдань четвертої частини державної підсумкової атестації з алгебри |
6 |
|
Алгебра |
|
|
Перетворення алгебраїчних виразів |
7 |
|
Кратність та подільність виразів |
8 |
|
Властивості функції |
8 |
|
Побудова графіків функцій, рівнянь та нерівностей |
9 |
|
Побудова на координатній площині рівнянь, нерівностей та їх систем |
9 |
|
Елементи комбінаторики та теорії ймовірностей |
10 |
|
Рівняння |
10 |
|
Теорема Вієта |
11 |
|
Рівняння з параметрами |
12 |
|
Нерівності |
15 |
|
Доведення нерівностей |
16 |
|
Нерівності з параметрами |
17 |
|
Системи рівнянь |
17 |
|
Системи рівнянь та нерівностей з параметрами |
19 |
|
Зразок виконання завдань четвертої частини державної підсумкової атестації з геометрії |
22 |
|
Геометрія |
|
|
Кути та відрізки на площині |
23 |
|
Трикутник та його елементи |
23 |
|
Доведення в трикутнику |
24 |
|
Геометричні побудови у трикутнику |
26 |
|
Площа трикутника |
26 |
|
Чотирикутник |
28 |
|
Паралелограм |
29 |
|
Прямокутник і квадрат |
29 |
|
Трапеція |
30 |
|
Коло та його елементи |
31 |
|
Вписаний та описаний трикутник |
33 |
|
Вписаний та описаний чотирикутник |
36 |
|
Координати |
37 |
|
Вектори |
38 |
|
Відповіді з алгебри |
39 |
|
Відповіді з геометрії |
51 |
|
Список використаної літератури |
56 |
Передмова
В наш час середня шкільна освіта в Україні передбачає обов’язкове отримання учнями систематизованих знань в галузі математики. Разом з тим, необхідність шкільної математичної, яка допоможе випускникам правильно орієнтуватися в житті сучасного суспільства і зробити правильний вибір життєвого шляху з урахуванням власних вподобань і особливостей характеру, настільки очевидна, що вимагає вміння орієнтуватися в питаннях, пов’язаних з математичними задачами як під час співіснування в суспільстві, так і в побуті.
Досвід показує, що таке навчання потрібне із застосуванням всіх наявних раціональних засобів для оволодіння програмним матеріалом математичними прийомами. Проте аналіз навчальної літератури підводить до висновку, що нині загальноосвітні навчальні заклади в Україні не в повній мірі забезпечені потрібними дидактичними матеріалами.
Даний посібник, який за своїм форматом є збірником задач, покликаний забезпечити дидактичним матеріалом учнів 9 класів на уроках математики під час розв’язування задач з математики підвищеного рівня складності, які містяться, у завданнях для державної підсумкової атестації та є у програмі для зовнішнього незалежного оцінювання школярів. Бажаним є використання цього видання для факультативних курсів за вибором вчителями математики у загальноосвітніх навчальних закладах. Основною метою даного посібника автор бачить у сприянні якісної підготовки здібних учнів до участі у предметних олімпіадах, конкурсах та при підготовці робіт слухачами Малої академії наук України.
Використання даного посібника має, перш за все, індивідуальну спрямованість, тобто його використання доцільне для конкретних учнів класу, які виявили здібності до вивчення математики. Збірник структурований як за навчальною програмою, затвердженою Міністерством освіти і науки України, так і за характером завдань: від завдань, що відповідають високому рівню навчальних досягнень, до задач для математичних гуртків і факультативів. Цінністю даного посібника також є те, що він містить відповіді до переважної більшості завдань, запропонованих до розв’язання. Збірник містить ряд задач, які певним чином є аналогічними до раніше розв’язаних, що може бути використано вчителем для запропонування учням опрацювання домашнього завдання.
Автор сподівається, що даний посібник допоможе учням виявити інтерес до вивчення математики за допомогою розв’язування задач підвищеного рівня складності.
Зразок виконання завдань четвертої частини державної
підсумкової атестації з алгебри
Приклад 1. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
Розв’язання. Рівняння рівносильне системі 
Розв’язуючи рівняння, матимемо:
![]() ;
;
![]() ;
; ![]() .
.
Рівняння, що задано в умові, має єдиний розв’язок в одному з таких випадків:
1) ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() .
.
Розглянемо ці випадки по черзі.
1) ![]() ;
; ![]() . У цьому випадку
. У цьому випадку ![]() . Отже,
. Отже, ![]() задовольняє умову задачі.
задовольняє умову задачі.
2) ![]() звідки
звідки ![]() .
.
3) ![]() звідки
звідки ![]() .
.
Відповідь: ![]() ;
; ![]() ;
; ![]() .
.
![]() Приклад 2. Знайдіть усі значення параметра
Приклад 2. Знайдіть усі значення параметра ![]() , при яких розв’язок системи нерівностей
, при яких розв’язок системи нерівностей 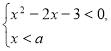 містить рівно два цілих числа.
містить рівно два цілих числа.
Розв’язання. Розв’язком першої нерівності системи є проміжок ![]() , зображений на рисунку.
, зображений на рисунку.
Розв’язком другої нерівності є проміжок ![]() . Для того, щоб переріз цих множин містив рівно два цілих числа, має виконуватись нерівність
. Для того, щоб переріз цих множин містив рівно два цілих числа, має виконуватись нерівність ![]() .
.
Відповідь: ![]() .
.
Приклад 3. Доведіть нерівність ![]() , де
, де ![]() і
і ![]() – довільні додатні числа.
– довільні додатні числа.
Розв’язання. Скориставшись нерівністю Коші для двох додатних чисел, маємо:
![]() ;
; ![]() .
.
Перемноживши відповідно ліві та праві частини записаних нерівностей, отримаємо:
![]() , що й треба було довести.
, що й треба було довести.
Приклад 4. Доведіть, що при будь-якому натуральному значенні ![]() виконується нерівність
виконується нерівність ![]() .
.
Розв’язання. Скористаємось методом математичної індукції. При ![]() маємо
маємо ![]() . Тобто базу індукції доведено. Нехай для натурального
. Тобто базу індукції доведено. Нехай для натурального ![]() виконується нерівність
виконується нерівність ![]() . Тоді виконується нерівність
. Тоді виконується нерівність ![]() . Крім того, при
. Крім того, при ![]() маємо
маємо ![]() . Отже,
. Отже, ![]() , що й доводить індуктивний перехід.
, що й доводить індуктивний перехід.

Перетворення алгебраїчних виразів
1. Розкладіть многочлен ![]() на лінійні множники.
на лінійні множники.
2. Доведіть, що при будь-якому натуральному значенні ![]() дріб
дріб ![]() є нескоротним.
є нескоротним.
3. Доведіть, що при будь-якому натуральному значенні ![]() дріб
дріб ![]() є нескоротним.
є нескоротним.
4. При яких натуральних значеннях ![]() значення виразу
значення виразу ![]() є простим числом?
є простим числом?
5. Знайдіть усі натуральні значення ![]() , при яких значення виразу
, при яких значення виразу ![]() є простим числом.
є простим числом.
6. Знайдіть усі прості числа ![]() такі, що числа
такі, що числа ![]() і
і ![]() також є простими.
також є простими.
7. Числа ![]() і
і ![]() є простими. Знайдіть число
є простими. Знайдіть число ![]() .
.
8. Доведіть, що при всіх цілих ![]() значення виразу
значення виразу ![]() є квадратом цілого числа.
є квадратом цілого числа.
9. Доведіть, що при всіх цілих ![]() значення виразу
значення виразу ![]() є квадратом цілого числа.
є квадратом цілого числа.
10. Доведіть, що для будь-якого натурального ![]() значення виразу
значення виразу ![]() є натуральним числом.
є натуральним числом.
11. Доведіть, що для будь-якого цілого ![]() виконується рівність
виконується рівність ![]() .
.
12. Знайдіть найбільше значення виразу ![]() .
.
13. Додатні числа ![]() і
і ![]() такі, що
такі, що ![]() . Знайдіть найбільше значення виразу
. Знайдіть найбільше значення виразу ![]() .
.
14. Додатні числа ![]() і
і ![]() такі, що
такі, що ![]() . Знайдіть найбільше значення виразу
. Знайдіть найбільше значення виразу ![]() .
.
15. Про додатні числа ![]() і
і ![]() відомо, що
відомо, що ![]() . Знайдіть значення виразу
. Знайдіть значення виразу ![]() .
.
16. Про додатні числа ![]() і
і ![]() відомо, що
відомо, що ![]() . Знайдіть значення виразу
. Знайдіть значення виразу ![]() .
.
17. Доведіть, що коли ![]() , то
, то ![]() .
.
18. Спростіть вираз 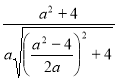 .
.
19. Спростіть вираз ![]() .
.
20. Доведіть, що значення виразу ![]() є цілим числом.
є цілим числом.
21. Доведіть, що значення виразу ![]() є цілим числом.
є цілим числом.
22. Спростіть вираз  і обчисліть його значення, якщо
і обчисліть його значення, якщо ![]() .
.
23. Обчисліть значення виразу  , якщо
, якщо ![]() .
.
24. Середнє арифметичне двох додатних чисел ![]() і
і ![]()
![]() у
у ![]() разів більше за їх середнє арифметичне. Доведіть, що
разів більше за їх середнє арифметичне. Доведіть, що  .
.
25. Спростіть вираз ![]() .
.
26. Спростіть вираз ![]() .
.
27. Знайдіть остачу від ділення числа ![]() на число
на число ![]() .
.
28. Число ![]() подайте у вигляді різниці кубів двох натуральних чисел. Доведіть, що таке подання єдине.
подайте у вигляді різниці кубів двох натуральних чисел. Доведіть, що таке подання єдине.
Кратність та подільність виразів
29. Відомо, що ціле число ![]() не кратне
не кратне ![]() . Доведіть, що значення виразу
. Доведіть, що значення виразу ![]() кратне
кратне ![]() .
.
30. Доведіть, що при будь-якому натуральному ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
31. Доведіть, що при будь-якому натуральному ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
32. Відомо, що ціле число ![]() не кратне
не кратне ![]() . Доведіть, що значення виразу
. Доведіть, що значення виразу ![]() кратне
кратне ![]() .
.
33. Доведіть, що при будь-якому натуральному ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
34. Доведіть, що при всіх натуральних значеннях ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
35. Доведіть, що при всіх натуральних значеннях ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
36. Доведіть, що при будь-якому натуральному ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
37. Доведіть, що для будь-якого натурального ![]() значення виразу
значення виразу ![]() кратне
кратне ![]() .
.
Властивості функції
38. Знайдіть усі значення параметра ![]() , при яких функція
, при яких функція ![]() визначена на множині дійсних чисел.
визначена на множині дійсних чисел.
39. Знайдіть усі значення параметра ![]() , при яких функція
, при яких функція ![]() визначена на множині дійсних чисел.
визначена на множині дійсних чисел.
40. Знайдіть усі значення параметра ![]() , при яких функція
, при яких функція ![]() є непарною.
є непарною.
41. Знайдіть усі значення параметра ![]() , при яких функція
, при яких функція ![]() є парною.
є парною.
Побудова графіків функцій, рівнянь та нерівностей
42. Побудуйте графік функції ![]() .
.
43. Побудуйте графік функції ![]() .
.
44. Побудуйте графік рівняння ![]() .
.
45. Побудуйте графік рівняння ![]() .
.
46. Побудуйте графік рівняння ![]() .
.
47. Побудуйте графік рівняння ![]() .
.
48. Побудуйте графік рівняння ![]() .
.
49. Побудуйте графік рівняння ![]() .
.
50. Побудуйте графік рівняння ![]() .
.
51. Побудуйте графік рівняння ![]() .
.
52. Побудуйте графік рівняння ![]() .
.
53. Побудуйте графік рівняння ![]() .
.
54. Побудуйте графік рівняння ![]() .
.
55. Побудуйте графік рівняння ![]() .
.
56. Побудуйте графік рівняння ![]() .
.
57. Побудуйте графік нерівності ![]() .
.
58. Побудуйте графік нерівності ![]() .
.
Побудова на координатній площині рівнянь, нерівностей та їх систем
59. Побудуйте на координатній площині множину точок, координати яких ![]() задовольняють рівність
задовольняють рівність ![]() .
.
60. Зобразіть на координатній площині множину точок, координати яких ![]() задовольняють рівність
задовольняють рівність ![]() .
.
61. Зобразіть на координатній площині множину точок, координати яких ![]() задовольняють рівність
задовольняють рівність ![]() .
.
62. Зобразіть на координатній площині множину точок, координати яких ![]() задовольняють нерівність
задовольняють нерівність ![]() .
.
63. Зобразіть на координатній площині множину точок, координати яких ![]() задовольняють нерівність
задовольняють нерівність ![]() .
.
64. Побудуйте на координатній площині множину точок, координати яких ![]() задовольняють нерівність
задовольняють нерівність ![]() .
.
65. Побудуйте на координатній площині множину точок, координати яких ![]() задовольняють систему нерівностей
задовольняють систему нерівностей 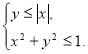
66. Побудуйте на координатній площині множину точок, координати яких ![]() задовольняють систему нерівностей
задовольняють систему нерівностей 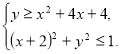
67. Побудуйте на координатній площині множину точок, координати яких ![]() задовольняють систему нерівностей
задовольняють систему нерівностей 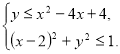
Елементи комбінаторики та теорії ймовірностей
68. У ![]() класі навчається
класі навчається ![]() учнів, а у
учнів, а у ![]() –
– ![]() учні. Для участі в шкільній конференції кожний клас делегує трьох учнів. Скільки існує способів сформувати делегацію від цих дев’ятих класів?
учні. Для участі в шкільній конференції кожний клас делегує трьох учнів. Скільки існує способів сформувати делегацію від цих дев’ятих класів?
69. У класі навчається ![]() учнів. Для вивчення іноземної мови їх треба розбити на три групи по
учнів. Для вивчення іноземної мови їх треба розбити на три групи по ![]() учнів. Скількома способами це можна зробити?
учнів. Скількома способами це можна зробити?
70. У шаховій секції займаються ![]() хлопців і
хлопців і ![]() дівчат. Скількома способами можна скласти команду з
дівчат. Скількома способами можна скласти команду з ![]() учнів так, щоб до цієї команди входило п’ять хлопців і дві дівчини?
учнів так, щоб до цієї команди входило п’ять хлопців і дві дівчини?
71. Є ![]() різних квіток. Скільки існує способів скласти з них букет з
різних квіток. Скільки існує способів скласти з них букет з ![]() квіток або з
квіток або з ![]() квіток?
квіток?
72. Прямі ![]() і
і ![]() паралельні. На прямій
паралельні. На прямій ![]() позначили
позначили ![]() точок
точок ![]() , а на прямій
, а на прямій ![]() –
– ![]() точок
точок ![]() . Скільки існує чотирикутників з вершинами в позначених точках?
. Скільки існує чотирикутників з вершинами в позначених точках?
73. Скільки існує чотирицифрових чисел, усі цифри яких мають однакову парність?
74. Скільки трицифрових чисел можна записати за допомогою цифр ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ?
?
75. Скільки трицифрових парних чисел можна записати за допомогою цифр ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ?
?
76. Скільки чотирицифрових непарних чисел можна записати за допомогою цифр ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ?
?
77. Скільки непарних семицифрових чисел можна записати за допомогою цифр ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() так, щоб у кожному числі цифри були різними?
так, щоб у кожному числі цифри були різними?
78. Дослід полягає в одночасному киданні трьох гральних кубиків. Знайдіть ймовірність того, що випадуть дві трійки і одна двійка.
79. Дослід полягає в одночасному киданні ![]() гральних кубиків. Знайдіть ймовірність того, що випадуть
гральних кубиків. Знайдіть ймовірність того, що випадуть ![]() різні цифри.
різні цифри.
80. Для лотереї підготували ![]() білетів, з яких
білетів, з яких ![]() є виграшними. Яка ймовірність того, що з трьох навмання вибраних білетів усі виявляться виграшними?
є виграшними. Яка ймовірність того, що з трьох навмання вибраних білетів усі виявляться виграшними?
81. У ящику лежать ![]() жовтих і
жовтих і ![]() синіх куль. Яка ймовірність того, що з вибраних навмання восьми куль п’ять будуть жовтими?
синіх куль. Яка ймовірність того, що з вибраних навмання восьми куль п’ять будуть жовтими?
82. У ящику знаходяться ![]() жовтих і
жовтих і ![]() синіх куль. Яка ймовірність того, що три навмання вибрані кулі будуть жовтими?
синіх куль. Яка ймовірність того, що три навмання вибрані кулі будуть жовтими?
83. У ящику лежать ![]() білих і
білих і ![]() чорних кульок. Яка ймовірність того, що серед трьох навмання обраних кульок буде
чорних кульок. Яка ймовірність того, що серед трьох навмання обраних кульок буде ![]() білі і
білі і ![]() чорна?
чорна?
Рівняння
84. Розв’яжіть рівняння ![]() .
.
85. Розв’яжіть рівняння ![]() .
.
86. Розв’яжіть рівняння ![]() .
.
87. Розв’яжіть рівняння ![]() .
.
88. Розв’яжіть рівняння ![]() .
.
89. Розв’яжіть рівняння ![]() .
.
90. Розв’яжіть рівняння ![]() .
.
91. Розв’яжіть рівняння ![]() .
.
92. Розв’яжіть рівняння ![]() .
.
93. Розв’яжіть рівняння ![]() .
.
94. Розв’яжіть рівняння ![]() .
.
95. Розв’яжіть рівняння ![]() .
.
96. Розв’яжіть рівняння ![]() .
.
97. Розв’яжіть рівняння ![]() .
.
98. Розв’яжіть рівняння 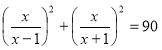 .
.
99. Розв’яжіть рівняння ![]() .
.
100. Розв’яжіть рівняння ![]() .
.
101. Розв’яжіть рівняння ![]() .
.
102. Розв’яжіть рівняння ![]() .
.
103. Розв’яжіть рівняння ![]() .
.
104. Розв’яжіть рівняння ![]() .
.
105. Розв’яжіть рівняння ![]() .
.
106. Розв’яжіть рівняння ![]() .
.
107. Розв’яжіть рівняння ![]() .
.
108. Розв’яжіть рівняння ![]() .
.
109. Розв’яжіть рівняння ![]() .
.
110. Розв’яжіть рівняння ![]() .
.
111. Розв’яжіть рівняння ![]() .
.
Теорема Вієта
112. Відомо, що ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() . Не розв’язуючи рівняння, знайдіть значення виразу
. Не розв’язуючи рівняння, знайдіть значення виразу ![]() .
.
113. Відомо, що ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() . Не розв’язуючи рівняння, знайдіть значення виразу
. Не розв’язуючи рівняння, знайдіть значення виразу ![]() .
.
114. Відомо, що ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() . Не розв’язуючи рівняння, знайдіть значення виразу
. Не розв’язуючи рівняння, знайдіть значення виразу ![]() .
.
115. Доведіть, що коли ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() , а
, а ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() , то
, то ![]() .
.
116. Числа ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() . Знайдіть значення
. Знайдіть значення ![]() , при яких виконується рівність
, при яких виконується рівність ![]() .
.
117. Відомо, що ![]() і
і ![]() – корені рівняння
– корені рівняння ![]() . Знайдіть значення
. Знайдіть значення ![]() , при яких виконується рівність
, при яких виконується рівність ![]() .
.
Рівняння з параметрами
118. При яких значеннях параметра ![]() має розв’язки рівняння
має розв’язки рівняння ![]() ?
?
119. При яких значеннях параметра ![]() сума квадратів коренів рівняння
сума квадратів коренів рівняння ![]() дорівнює
дорівнює ![]() ?
?
120. При яких значеннях параметра ![]() сума квадратів коренів рівняння
сума квадратів коренів рівняння ![]() дорівнює
дорівнює ![]() ?
?
121. Знайдіть усі значення параметра ![]() , при яких сума коренів рівняння
, при яких сума коренів рівняння ![]() дорівнює
дорівнює ![]() .
.
122. Знайдіть усі значення параметра ![]() , при яких сума коренів рівняння
, при яких сума коренів рівняння ![]() дорівнює
дорівнює ![]() .
.
123. Знайдіть усі значення параметра ![]() , при яких сума коренів рівняння
, при яких сума коренів рівняння ![]() дорівнює
дорівнює ![]() .
.
124. При яких значеннях параметра ![]() один з коренів рівняння
один з коренів рівняння ![]() утричі більший за другий?
утричі більший за другий?
125. При яких значеннях параметра ![]() рівняння
рівняння ![]() має корені різного знаку?
має корені різного знаку?
126. При яких значеннях параметра ![]() рівняння
рівняння ![]() має корені різного знаку?
має корені різного знаку?
127. При яких значеннях параметра ![]() корені рівняння
корені рівняння ![]() є додатними числами?
є додатними числами?
128. При яких значеннях параметра ![]() корені рівняння
корені рівняння ![]() є від’ємними числами?
є від’ємними числами?
129. Доведіть, що рівняння ![]() має хоча б один корінь при будь-яких дійсних значеннях
має хоча б один корінь при будь-яких дійсних значеннях ![]() і
і ![]() .
.
130. При яких значеннях параметра ![]() обидва корені рівняння
обидва корені рівняння ![]() належать проміжку
належать проміжку ![]() ?
?
131. При яких значеннях параметра ![]() рівняння
рівняння ![]() має рівно два різних корені?
має рівно два різних корені?
132. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три корені?
має три корені?
133. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три корені?
має три корені?
134. Скільки розв’язків має рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() ?
?
135. Скільки розв’язків має рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() ?
?
136. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
137. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
138. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний корінь?
має єдиний корінь?
139. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
140. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний корінь?
має єдиний корінь?
141. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
142. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
143. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
144. Визначте кількість розв’язків рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
145. Визначте кількість розв’язків рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
146. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
147. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
148. Скільки коренів має рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() ?
?
149. Скільки коренів має рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() ?
?
150. Визначте кількість коренів рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
151. Визначте кількість коренів рівняння ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
152. Скільки розв’язків залежно від значення параметра ![]() має рівняння
має рівняння ![]() ?
?
153. Скільки розв’язків залежно від значення параметра ![]() має рівняння
має рівняння ![]() .
.
154. При яких значеннях параметра ![]() множиною коренів рівняння
множиною коренів рівняння ![]() є числовий відрізок, довжина якого дорівнює
є числовий відрізок, довжина якого дорівнює ![]() ?
?
155. При яких значеннях параметра ![]() множиною розв’язків рівняння
множиною розв’язків рівняння ![]() є числовий відрізок, довжина якого дорівнює
є числовий відрізок, довжина якого дорівнює ![]() ?
?
156. При яких значеннях параметра ![]() рівняння
рівняння ![]() має шість розв’язків?
має шість розв’язків?
157. Знайдіть усі значення параметра ![]() , при яких рівняння
, при яких рівняння ![]() має безліч розв’язків.
має безліч розв’язків.
158. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
159. При яких значеннях параметра ![]() рівняння
рівняння 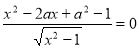 не має коренів?
не має коренів?
160. При яких значеннях параметра ![]() рівняння
рівняння  має один розв’язок?
має один розв’язок?
161. При яких значеннях параметра ![]() рівняння
рівняння 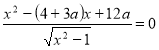 має єдиний розв’язок?
має єдиний розв’язок?
162. При яких значеннях параметра ![]() рівняння
рівняння 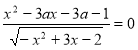 має один розв’язок?
має один розв’язок?
163. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
164. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний розв’язок?
має єдиний розв’язок?
165. При яких значеннях параметра ![]() рівняння
рівняння ![]() має єдиний корінь?
має єдиний корінь?
166. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три розв’язки?
має три розв’язки?
167. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три розв’язки?
має три розв’язки?
168. При яких значеннях параметра ![]() рівняння
рівняння ![]() має два різних додатних корені?
має два різних додатних корені?
169. При яких значеннях параметра ![]() рівняння
рівняння ![]() має два різних від’ємних корені?
має два різних від’ємних корені?
170. При яких раціональних значеннях параметрів ![]() і
і ![]() один із коренів рівняння
один із коренів рівняння ![]() дорівнює
дорівнює ![]() ?
?
171. При яких раціональних значеннях параметрів ![]() і
і ![]() один із коренів рівняння
один із коренів рівняння ![]() дорівнює
дорівнює ![]() ?
?
172. Для кожного значення параметра ![]() вкажіть кількість коренів рівняння
вкажіть кількість коренів рівняння ![]() .
.
173. Для кожного значення параметра ![]() з’ясуйте кількість коренів рівняння
з’ясуйте кількість коренів рівняння ![]() .
.
174. Знайдіть усі значення параметра ![]() , при яких рівняння
, при яких рівняння ![]() має три корені.
має три корені.
175. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
176. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
177. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
178. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
179. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
180. Для кожного значення параметра ![]() розв’яжіть рівняння
розв’яжіть рівняння ![]() .
.
181. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три різних корені?
має три різних корені?
182. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три різних корені?
має три різних корені?
183. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три дійсних корені, які утворюють геометричну прогресію?
має три дійсних корені, які утворюють геометричну прогресію?
184. При яких значеннях параметра ![]() рівняння
рівняння ![]() має три дійсних корені, які утворюють геометричну прогресію?
має три дійсних корені, які утворюють геометричну прогресію?
Нерівності
185. Розв’яжіть нерівність ![]() .
.
186. Розв’яжіть нерівність ![]() .
.
187. Розв’яжіть нерівність ![]() .
.
188. Знайдіть множину розв’язків нерівності ![]() .
.
189. Знайдіть множину розв’язків нерівності ![]() .
.
190. Знайдіть множину розв’язків нерівності ![]() .
.
191. Знайдіть множину розв’язків нерівності ![]() .
.
192. Розв’яжіть нерівність ![]() .
.
193. Розв’яжіть нерівність ![]() .
.
194. Розв’яжіть нерівність ![]() .
.
195. Розв’яжіть нерівність ![]() .
.
196. Розв’яжіть нерівність ![]() .
.
197. Розв’яжіть нерівність ![]() .
.
198. Розв’яжіть нерівність ![]() .
.
199. Розв’яжіть нерівність ![]() .
.
200. Розв’яжіть нерівність ![]() .
.
201. Розв’яжіть нерівність ![]() .
.
202. Розв’яжіть нерівність ![]() .
.
203. Розв’яжіть нерівність ![]() .
.
204. Розв’яжіть нерівність ![]() .
.
205. Розв’яжіть нерівність ![]() .
.
206. Розв’яжіть нерівність ![]() .
.
207. Розв’яжіть нерівність ![]() .
.
208. Знайдіть найбільше ціле число, яке є розв’язком нерівності ![]() .
.
209. Знайдіть найменший цілий розв’язок нерівності ![]() .
.
210. Розв’яжіть нерівність ![]() .
.
211. Розв’яжіть нерівність ![]() .
.
212. Розв’яжіть нерівність ![]() .
.
213. Розв’яжіть нерівність ![]() .
.
214. Розв’яжіть нерівність ![]() .
.
215. Розв’яжіть нерівність ![]() .
.
216. Розв’яжіть нерівність ![]() .
.
217. Розв’яжіть нерівність ![]() .
.
218. Розв’яжіть нерівність ![]() .
.
219. Розв’яжіть нерівність ![]() .
.
220. Розв’яжіть нерівність ![]() .
.
Доведення нерівностей
221. Для будь-яких дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
222. Для будь-яких дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
223. Для довільних дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
224. Для всіх дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
225. Для будь-яких дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
226. Для всіх дійсних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
227. Для всіх дійсних ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
228. Дійсні числа ![]() і
і ![]() задовольняють умову
задовольняють умову ![]() . Доведіть, що
. Доведіть, що ![]() .
.
229. Дійсні числа ![]() і
і ![]() задовольняють умову
задовольняють умову ![]() . Доведіть, що
. Доведіть, що ![]() .
.
230. Доведіть, що для будь-яких додатних чисел ![]() ,
, ![]() і
і ![]() виконується нерівність
виконується нерівність ![]() .
.
231. Для довільного дійсного ![]() доведіть нерівність
доведіть нерівність ![]() . При яких значеннях
. При яких значеннях ![]() виконується нерівність?
виконується нерівність?
232. Доведіть, що нерівність ![]() виконується при всіх дійсних значеннях
виконується при всіх дійсних значеннях ![]() .
.
233. Доведіть нерівність ![]() для всіх дійсних значень
для всіх дійсних значень ![]() і знайдіть усі значення
і знайдіть усі значення ![]() , при яких виконується рівність.
, при яких виконується рівність.
234. Доведіть нерівність ![]() для всіх дійсних значень
для всіх дійсних значень ![]() .
.
235. Для невід’ємних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
236. Для додатних чисел ![]() і
і ![]() доведіть нерівність
доведіть нерівність ![]() .
.
237. Доведіть, що коли ![]() і
і ![]() , то
, то  .
.
238. Доведіть, що для будь-яких додатних чисел ![]() і
і ![]() виконується нерівність
виконується нерівність ![]() .
.
239. Числа ![]() ,
, ![]() ,
, ![]() такі, що
такі, що ![]() . Доведіть, що
. Доведіть, що ![]() .
.
240. Доведіть, що коли ![]() ,
, ![]() ,
, ![]() , то
, то ![]() .
.
241. Доведіть нерівність ![]() ,
, ![]() ,
, ![]() .
.
242. Доведіть нерівність ![]() ,
, ![]() ,
, ![]() .
.
Нерівності з параметрами
243. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
244. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
245. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
246. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
247. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
248. Знайдіть розв’язки нерівності ![]() залежно від значення параметра
залежно від значення параметра ![]() .
.
249. Знайдіть розв’язки нерівності залежно від значення параметра ![]()
![]() .
.
250. Знайдіть усі значення параметра ![]() , при яких нерівність
, при яких нерівність ![]() виконується для всіх дійсних значень
виконується для всіх дійсних значень ![]() .
.
251. Знайдіть усі значення параметра ![]() , при яких нерівність
, при яких нерівність ![]() виконується при всіх дійсних значеннях
виконується при всіх дійсних значеннях ![]() .
.
252. При яких значеннях параметра ![]() нерівність
нерівність ![]() виконується при всіх додатних значеннях
виконується при всіх додатних значеннях ![]() ?
?
253. При яких значеннях параметра ![]() нерівність
нерівність ![]() виконується при всіх від’ємних значеннях
виконується при всіх від’ємних значеннях ![]() ?
?
254. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
255. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
256. Для кожного значення параметра ![]() розв’яжіть нерівність
розв’яжіть нерівність ![]() .
.
Системи рівнянь
257. Розв’яжіть систему рівнянь 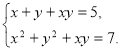
258. Розв’яжіть систему рівнянь 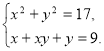
259. Розв’яжіть систему рівнянь 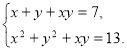
260. Розв’яжіть систему рівнянь 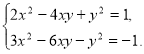
261. Розв’яжіть систему рівнянь 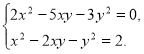
262. Розв’яжіть систему рівнянь 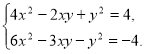
263. Розв’яжіть систему рівнянь 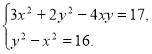
264. Розв’яжіть систему рівнянь 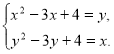
265. Розв’яжіть систему рівнянь 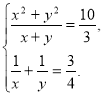
266. Розв’яжіть систему рівнянь 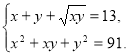
267. Розв’яжіть систему рівнянь 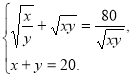
268. Розв’яжіть систему рівнянь ![]()
269. Розв’яжіть систему рівнянь ![]()
270. Розв’яжіть систему рівнянь 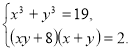
271. Розв’яжіть систему рівнянь 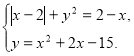
272. Розв’яжіть систему рівнянь 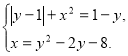
273. Розв’яжіть систему рівнянь 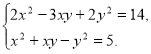
274. Розв’яжіть систему рівнянь 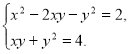
275. Розв’яжіть систему рівнянь ![]()
276. Розв’яжіть систему рівнянь ![]()
277. Розв’яжіть систему рівнянь 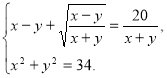
278. Розв’яжіть систему рівнянь 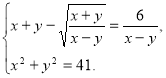
279. Розв’яжіть систему рівнянь 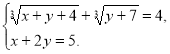
280. Розв’яжіть систему рівнянь 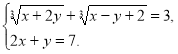
281. Розв’яжіть систему рівнянь 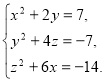
282. Розв’яжіть систему рівнянь 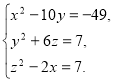
283. Розв’яжіть систему рівнянь 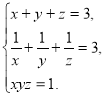
284. Розв’яжіть систему рівнянь 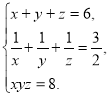
Системи рівнянь та нерівностей з параметрами
285. При яких значеннях параметра ![]() система рівнянь
система рівнянь ![]() має безліч розв’язків?
має безліч розв’язків?
286. При яких значеннях параметра ![]() система рівнянь
система рівнянь ![]() має безліч розв’язків?
має безліч розв’язків?
287. При яких значеннях параметра ![]() система рівнянь
система рівнянь ![]() має безліч розв’язків?
має безліч розв’язків?
288. При яких значеннях параметра ![]() система рівнянь
система рівнянь ![]() не має розв’язків?
не має розв’язків?
289. Для кожного значення параметра ![]() знайдіть кількість розв’язків системи рівнянь
знайдіть кількість розв’язків системи рівнянь 
290. Для кожного значення параметра ![]() знайдіть кількість розв’язків системи рівнянь
знайдіть кількість розв’язків системи рівнянь 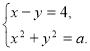
291. При яких значеннях параметра ![]() система рівнянь
система рівнянь ![]() не має розв’язків?
не має розв’язків?
292. При яких значеннях параметра ![]() система рівнянь
система рівнянь 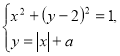 має три розв’язки?
має три розв’язки?
293. При яких значеннях параметра ![]() система рівнянь
система рівнянь 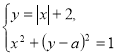 має три розв’язки?
має три розв’язки?
294. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь 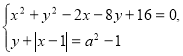 має єдиний розв’язок.
має єдиний розв’язок.
295. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь 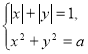 не має розв’язків.
не має розв’язків.
296. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь 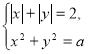 має чотири розв’язки.
має чотири розв’язки.
297. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь 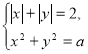 має чотири розв’язки.
має чотири розв’язки.
298. При яких значеннях параметра ![]() система
система ![]() має розв’язки при будь-якому значенні параметра
має розв’язки при будь-якому значенні параметра ![]() ?
?
299. При яких значеннях параметра ![]() система
система ![]() має розв’язки при будь-якому значенні параметра
має розв’язки при будь-якому значенні параметра ![]() ?
?
300. Визначте кількість розв’язків системи 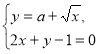 залежно від значення параметра
залежно від значення параметра ![]() .
.
301. Визначте кількість розв’язків системи  залежно від значення параметра
залежно від значення параметра ![]() .
.
302. При яких значеннях параметра ![]() система
система ![]() має безліч розв’язків?
має безліч розв’язків?
303. При яких значеннях параметра ![]() система
система ![]() не має розв’язків?
не має розв’язків?
304. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь ![]() має безліч розв’язків.
має безліч розв’язків.
305. Знайдіть усі значення параметра ![]() , при яких система рівнянь
, при яких система рівнянь ![]() не має розв’язків.
не має розв’язків.
306. При якому найменшому значенні параметра ![]() система рівнянь
система рівнянь 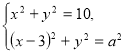 має єдиний розв’язок?
має єдиний розв’язок?
307. Знайдіть найменше значення параметра ![]() , при якому система рівнянь
, при якому система рівнянь 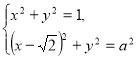 має єдиний розв’язок.
має єдиний розв’язок.
308. При яких значеннях параметра ![]() система рівнянь
система рівнянь 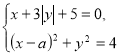 має три розв’язки?
має три розв’язки?
309. При яких значеннях параметра ![]() система рівнянь
система рівнянь 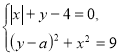 має один розв’язок?
має один розв’язок?
310. При якому значенні параметра ![]() система рівнянь
система рівнянь 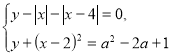 має єдиний розв’язок?
має єдиний розв’язок?
311. Знайдіть усі значення параметра ![]() , при яких множина розв’язків системи нерівностей
, при яких множина розв’язків системи нерівностей 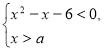 містить рівно три цілих числа.
містить рівно три цілих числа.
312. Знайдіть усі значення параметра ![]() , при яких множина розв’язків системи нерівностей
, при яких множина розв’язків системи нерівностей 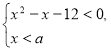 містить рівно три цілих числа.
містить рівно три цілих числа.
313. При яких значеннях параметра ![]() множиною розв’язків системи нерівностей
множиною розв’язків системи нерівностей ![]() є числовий відрізок, довжина якого дорівнює
є числовий відрізок, довжина якого дорівнює ![]() ?
?
314. При яких значеннях параметра ![]() множиною розв’язків системи нерівностей
множиною розв’язків системи нерівностей ![]() є числовий відрізок, довжина якого дорівнює
є числовий відрізок, довжина якого дорівнює ![]() ?
?
Зразок виконання завдань четвертої частини державної
підсумкової атестації з геометрії
Приклад 1. Через деяку точку всередині трикутника паралельно його сторонам проведено три прямі. Ці прямі ділять трикутник на шість частин, три з яких – трикутники. Площі цих трикутників дорівнюють ![]() ,
, ![]() і
і ![]() . Знайдіть площу даного трикутника.
. Знайдіть площу даного трикутника.
Розв’язання. Позначимо довжини відрізків ![]() ,
, ![]() ,
, ![]() .З паралельності прямих
.З паралельності прямих ![]() ,
, ![]() і
і ![]() відповідним сторонам
відповідним сторонам ![]() випливає, що кожний з отриманих трикутників
випливає, що кожний з отриманих трикутників ![]() ,
, ![]() ,
, ![]() подібний трикутнику
подібний трикутнику ![]() (за двома кутами).
(за двома кутами).
 Якщо шукану площу трикутника
Якщо шукану площу трикутника ![]() позначити через
позначити через ![]() , то за властивістю площ подібних трикутників можна записати такі три рівності:
, то за властивістю площ подібних трикутників можна записати такі три рівності:
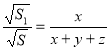 ;
; 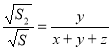 ;
;  .
.
Додавши почленно ці три рівності, отримаємо:
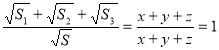 .
.
Звідси маємо, ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
Приклад 2. Центр кола, яке дотикається катетів прямокутного трикутника, належить гіпотенузі цього трикутника. Знайдіть радіус кола, якщо його центр ділить гіпотенузу на відрізки завдовжки ![]() см і
см і ![]() см.
см.
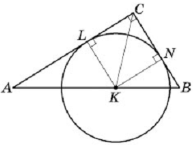 Розв’язання. На рисунку зображено прямокутний трикутник
Розв’язання. На рисунку зображено прямокутний трикутник ![]()
![]() , точка
, точка ![]() – центр кола, яке дотикається катетів
– центр кола, яке дотикається катетів ![]() і
і ![]() ,
, ![]() см,
см, ![]() см.
см.
![]() – точка дотику кола катета
– точка дотику кола катета ![]() ;
; ![]() – точка дотику кола катета
– точка дотику кола катета ![]() ;
; ![]() – радіус кола.
– радіус кола. ![]() (за катетом і гіпотенузою), тому
(за катетом і гіпотенузою), тому ![]() і
і ![]() – бісектриса
– бісектриса ![]() . За властивістю бісектриси
. За властивістю бісектриси ![]() ;
; ![]() .
.
Позначимо ![]() ;
; ![]() . Тоді
. Тоді ![]() ;
; ![]() ;
; ![]() см;
см; ![]() см.
см.
Площа ![]() трикутника
трикутника ![]() :
: ![]() (см2).
(см2).
Але, ![]() .
.
Маємо, ![]() ;
; ![]() (см).
(см).
Відповідь: ![]() см.
см.
Приклад 3. Дано коло ![]() . Знайдіть рівняння кола, центром якого є точка
. Знайдіть рівняння кола, центром якого є точка ![]() , яке дотикається до даного кола.
, яке дотикається до даного кола.
Розв’язання. Коло, що задане рівнянням ![]() , має центр у точці
, має центр у точці ![]() , радіус, що дорівнює
, радіус, що дорівнює ![]() . Відстань між точками
. Відстань між точками ![]() і
і ![]() дорівнює:
дорівнює: ![]() . Якщо кола дотикаються зовнішньо, то радіус шуканого кола дорівнює
. Якщо кола дотикаються зовнішньо, то радіус шуканого кола дорівнює ![]() . Тоді рівняння цього кола має вигляд:
. Тоді рівняння цього кола має вигляд: ![]() . Якщо шукане і подане кола дотикаються внутрішнім чином, то радіус шуканого кола дорівнює
. Якщо шукане і подане кола дотикаються внутрішнім чином, то радіус шуканого кола дорівнює ![]() і його рівняння має вигляд:
і його рівняння має вигляд: ![]() .
.
Відповідь: ![]() або
або ![]() .
.

Кути та відрізки на площині
315. Точки ![]() і
і ![]() лежать у різних півплощинах відносно прямої
лежать у різних півплощинах відносно прямої ![]() . На прямій
. На прямій ![]() знайдіть таку точку
знайдіть таку точку ![]() , щоб пряма
, щоб пряма ![]() містила бісектрису кута
містила бісектрису кута ![]() .
.
316. Точки ![]() і
і ![]() лежать в одній півплощині відносно прямої
лежать в одній півплощині відносно прямої ![]() . Знайдіть на прямій
. Знайдіть на прямій ![]() таку точку
таку точку ![]() , щоб промені
, щоб промені ![]() і
і ![]() утворювали з цією прямою рівні кути.
утворювали з цією прямою рівні кути.
317. Точки ![]() і
і ![]() лежать в одній півплощині відносно прямої
лежать в одній півплощині відносно прямої ![]() . Знайдіть на прямій
. Знайдіть на прямій ![]() таку точку
таку точку ![]() , щоб сума
, щоб сума ![]() була найменшою.
була найменшою.
318. З точки ![]() , яка належить куту
, яка належить куту ![]() , на його сторони опустили перпендикуляри завдовжки
, на його сторони опустили перпендикуляри завдовжки ![]() см і
см і ![]() см. Знайдіть відрізок
см. Знайдіть відрізок ![]() , якщо
, якщо ![]() .
.
319. З точки ![]() , розташованої всередині гострого кута
, розташованої всередині гострого кута ![]() , проведено перпендикуляри
, проведено перпендикуляри ![]() і
і ![]() до прямих
до прямих ![]() і
і ![]() відповідно. Доведіть, що
відповідно. Доведіть, що ![]() .
.
320. У внутрішній області кута ![]() розташовано точку на відстанях
розташовано точку на відстанях ![]() см і
см і ![]() см від сторін кута. Знайдіть відстань від цієї точки до вершини кута.
см від сторін кута. Знайдіть відстань від цієї точки до вершини кута.
321. Усередині кута ![]() позначено точку
позначено точку ![]() , проекціями якої на прямі
, проекціями якої на прямі ![]() і
і ![]() є точки
є точки ![]() і
і ![]() . Доведіть, що
. Доведіть, що ![]() .
.
Трикутник та його елементи
322. Медіана ![]() трикутника
трикутника ![]() дорівнює
дорівнює ![]() і утворює зі сторонами
і утворює зі сторонами ![]() і
і ![]() кути
кути ![]() і
і ![]() відповідно. Знайдіть сторону
відповідно. Знайдіть сторону ![]() .
.
323. Медіана ![]() трикутника
трикутника ![]() утворює зі сторонами
утворює зі сторонами ![]() і
і ![]() кути
кути ![]() і
і ![]() відповідно,
відповідно, ![]() . Знайдіть медіану
. Знайдіть медіану ![]() .
.
324. Медіана ![]() трикутника
трикутника ![]() дорівнює
дорівнює ![]() і утворює зі сторонами
і утворює зі сторонами ![]() і
і ![]() кути
кути ![]() і
і ![]() відповідно. Знайдіть довжини сторін
відповідно. Знайдіть довжини сторін ![]() і
і ![]() .
.
325. На стороні ![]() трикутника
трикутника ![]() позначено точку
позначено точку ![]() так, що
так, що ![]() . У якому відношенні медіана
. У якому відношенні медіана ![]() ділить відрізок
ділить відрізок ![]() ?
?
326. На стороні ![]() трикутника
трикутника ![]() позначено точку
позначено точку ![]() так, що
так, що ![]() . У якому відношенні відрізок
. У якому відношенні відрізок ![]() ділить медіану
ділить медіану ![]() ?
?
327. На стороні ![]() трикутника
трикутника ![]() позначено точку
позначено точку ![]() так, що
так, що ![]() . У якому відношенні відрізок
. У якому відношенні відрізок ![]() ділить медіану
ділить медіану ![]() трикутника
трикутника ![]() ?
?
328. На стороні ![]() трикутника
трикутника ![]() позначено точку
позначено точку ![]() так, що
так, що ![]() . У якому відношенні медіана
. У якому відношенні медіана ![]() трикутника
трикутника ![]() ділить відрізок
ділить відрізок ![]() ?
?
329. У трикутнику ![]() відрізок
відрізок ![]() (точка
(точка ![]() належить стороні
належить стороні ![]() ) ділить медіану
) ділить медіану ![]() у відношенні
у відношенні ![]() , рахуючи від вершини
, рахуючи від вершини ![]() . У якому відношенні точка
. У якому відношенні точка ![]() ділить сторону
ділить сторону ![]() ?
?
330. У трикутнику ![]() медіана
медіана ![]() ділить відрізок
ділить відрізок ![]() (точка
(точка ![]() належить стороні
належить стороні ![]() ) у відношенні
) у відношенні ![]() , рахуючи від вершини
, рахуючи від вершини ![]() . У якому відношенні точка
. У якому відношенні точка ![]() ділить сторону
ділить сторону ![]() ?
?
331. Периметр прямокутного трикутника ![]()
![]() дорівнює
дорівнює ![]() см, а різниця між довжиною медіани
см, а різниця між довжиною медіани ![]() і висоти
і висоти ![]() дорівнює
дорівнює ![]() см. Знайдіть довжину гіпотенузи трикутника.
см. Знайдіть довжину гіпотенузи трикутника.
332. Периметр прямокутного трикутника дорівнює ![]() см. Знайдіть його сторони, якщо висота, проведена до гіпотенузи, дорівнює
см. Знайдіть його сторони, якщо висота, проведена до гіпотенузи, дорівнює ![]() см.
см.
333. На сторонах ![]() і
і ![]() правильного трикутника
правильного трикутника ![]() позначено точки
позначено точки ![]() і
і ![]() відповідно так, що
відповідно так, що ![]() . Знайдіть кут
. Знайдіть кут ![]() , де точка
, де точка ![]() – центр трикутника.
– центр трикутника.
334. Основа рівнобедреного трикутника дорівнює ![]() см, а бічна сторона –
см, а бічна сторона – ![]() см. До бічних сторін трикутника проведено висоти. Обчисліть довжину відрізка, що сполучає основи цих висот.
см. До бічних сторін трикутника проведено висоти. Обчисліть довжину відрізка, що сполучає основи цих висот.
335. У рівнобедреному трикутнику кут при основі дорівнює ![]() , а бісектриса цього кута має довжину
, а бісектриса цього кута має довжину ![]() . Знайдіть довжини сторін трикутника.
. Знайдіть довжини сторін трикутника.
336. У рівнобедреному трикутнику висота, проведена до основи, дорівнює ![]() см, а висота, проведена до бічної сторони, –
см, а висота, проведена до бічної сторони, – ![]() см. Знайдіть периметр трикутника.
см. Знайдіть периметр трикутника.
337. У рівнобедреному трикутнику ![]()
![]() проведено бісектриси
проведено бісектриси ![]() і
і ![]() . Знайдіть кути трикутника
. Знайдіть кути трикутника ![]() , якщо
, якщо ![]() .
.
338. У прямокутному трикутнику ![]()
![]() відрізки
відрізки ![]() ,
, ![]() і
і ![]() – відповідно висота, бісектриса і медіана трикутника. Знайдіть бісектрису
– відповідно висота, бісектриса і медіана трикутника. Знайдіть бісектрису ![]() , якщо
, якщо ![]() см,
см, ![]() см.
см.
339. Серединний перпендикуляр гіпотенузи ![]() прямокутного трикутника
прямокутного трикутника ![]() перетинає катет
перетинає катет ![]() у точці
у точці ![]() . Відомо, що
. Відомо, що ![]() . Знайдіть гострі кути трикутника
. Знайдіть гострі кути трикутника ![]() .
.
340. У трикутнику ![]()
![]() медіани
медіани ![]() і
і ![]() перпендикулярні. Знайдіть
перпендикулярні. Знайдіть ![]() .
.
341. Усередині прямокутного трикутника ![]()
![]() взято точку
взято точку ![]() так, що трикутники
так, що трикутники ![]() ,
, ![]() і
і ![]() – рівновеликі. Знайдіть довжину відрізка
– рівновеликі. Знайдіть довжину відрізка ![]() , коли відомо, що
, коли відомо, що ![]() , де
, де ![]() .
.
342. У прямокутному трикутнику менший кут дорівнює ![]() . Перпендикулярно до гіпотенузи проведено пряму, яка ділить трикутник на дві рівновеликі частини. Знайдіть відношення, у якому ця пряма ділить гіпотенузу.
. Перпендикулярно до гіпотенузи проведено пряму, яка ділить трикутник на дві рівновеликі частини. Знайдіть відношення, у якому ця пряма ділить гіпотенузу.
343. У прямокутному трикутнику ![]()
![]() відрізок
відрізок ![]() – висота. Бісектриси прямих кутів трикутників
– висота. Бісектриси прямих кутів трикутників ![]() і
і ![]() відповідно дорівнюють
відповідно дорівнюють ![]() і
і ![]() . Знайдіть бісектрису прямого кута трикутника
. Знайдіть бісектрису прямого кута трикутника ![]() .
.
344. У трикутнику ![]() проведено медіану
проведено медіану ![]() . Відомо, що
. Відомо, що ![]() і
і ![]() . Знайдіть кут
. Знайдіть кут ![]() .
.
345. Відрізки ![]() і
і ![]() – бісектриси трикутника
– бісектриси трикутника ![]() . Знайдіть кут
. Знайдіть кут ![]() , якщо промінь
, якщо промінь ![]() – бісектриса кута
– бісектриса кута ![]() .
.
346. Одна із сторін трикутника дорівнює ![]() см, висота, що проведена до цієї сторони, дорівнює
см, висота, що проведена до цієї сторони, дорівнює ![]() см. Знайдіть дві інші сторони трикутника, якщо його периметр дорівнює
см. Знайдіть дві інші сторони трикутника, якщо його периметр дорівнює ![]() см.
см.
347. Дві сторони гострокутного трикутника дорівнюють ![]() см і
см і ![]() см. Знайдіть третю сторону, якщо вона дорівнює проведеній до неї висоті.
см. Знайдіть третю сторону, якщо вона дорівнює проведеній до неї висоті.
348. Дві сторони трикутника дорівнюють ![]() см і
см і ![]() см. Медіани, проведені до цих сторін, взаємно перпендикулярні. Знайдіть третю сторону трикутника.
см. Медіани, проведені до цих сторін, взаємно перпендикулярні. Знайдіть третю сторону трикутника.
349. У трикутнику ![]() довжина висоти
довжина висоти ![]() дорівнює
дорівнює ![]() см. Медіана
см. Медіана ![]() і бісектриса
і бісектриса ![]() ділять
ділять ![]() на три рівні частини. Знайдіть довжину сторони
на три рівні частини. Знайдіть довжину сторони ![]() .
.
350. У трикутнику висота і медіана, проведені з однієї вершини, ділять кут при цій вершині на три рівні частини. Знайдіть кути трикутника.
Доведення в трикутнику
351. Доведіть ознаку рівності трикутників за медіаною та кутами, на які вона ділить кут трикутника.
352. Доведіть ознаку рівності трикутників за двома сторонами і медіаною, проведеною до третьої сторони.
353. Доведіть, що в будь-якому трикутнику сума довжин медіан менша за периметр трикутника.
354. Доведіть, що сума квадратів двох сторін трикутника дорівнює подвоєній сумі квадратів половини третьої сторони і медіани, проведеної до цієї сторони.
355. У внутрішній області рівностороннього трикутника взято точку. Доведіть, що сума відстаней від цієї точки до сторін трикутника дорівнює висоті трикутника.
356. Доведіть, що сума відстаней від будь-якої точки, взятої на стороні правильного трикутника, до двох його інших сторін є сталою величиною.
357. У трикутнику ![]() точка
точка ![]() – основа бісектриси, проведеної з вершини
– основа бісектриси, проведеної з вершини ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
358. У трикутнику ![]() точка
точка ![]() – основа бісектриси, проведеної з вершини
– основа бісектриси, проведеної з вершини ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
359. У трикутнику ![]() відомо, що
відомо, що ![]() ,
, ![]() . Серединний перпендикуляр відрізка
. Серединний перпендикуляр відрізка ![]() перетинає його в точці
перетинає його в точці ![]() , а сторону
, а сторону ![]() – у точці
– у точці ![]() . Доведіть, що
. Доведіть, що ![]() .
.
360. Один з кутів прямокутного трикутника дорівнює ![]() . Доведіть, що висота трикутника, проведена до його гіпотенузи, у
. Доведіть, що висота трикутника, проведена до його гіпотенузи, у ![]() рази менша гіпотенузи.
рази менша гіпотенузи.
361. У трикутнику ![]() відомо, що
відомо, що ![]() ,
, ![]() см,
см, ![]() см. Доведіть, що його медіани
см. Доведіть, що його медіани ![]() і
і ![]() перпендикулярні.
перпендикулярні.
362. У трикутнику ![]() проведено медіану
проведено медіану ![]() . Відомо, що
. Відомо, що ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
363. Висота прямокутного трикутника, проведена до гіпотенузи, у ![]() рази менша гіпотенузи. Доведіть, що один із гострих кутів даного трикутника дорівнює
рази менша гіпотенузи. Доведіть, що один із гострих кутів даного трикутника дорівнює ![]() .
.
364. Відрізок ![]() – бісектриса трикутника
– бісектриса трикутника ![]() . На стороні
. На стороні ![]() позначили точку
позначили точку ![]() так, що
так, що ![]() . Доведіть, що промінь
. Доведіть, що промінь ![]() – бісектриса кута
– бісектриса кута ![]() .
.
365. Відрізок ![]() – медіана трикутника
– медіана трикутника ![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що
. Доведіть, що ![]() .
.
366. Бісектриси кутів ![]() і
і ![]() трикутника
трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . На сторонах
. На сторонах ![]() і
і ![]() позначено відповідно точки
позначено відповідно точки ![]() і
і ![]() такі, що
такі, що ![]() і
і ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() і
і ![]() лежать на одній прямій.
лежать на одній прямій.
367. Висоти трикутника дорівнюють ![]() см,
см, ![]() см і
см і ![]() см. Доведіть, що трикутник прямокутний.
см. Доведіть, що трикутник прямокутний.
368. У прямокутному трикутнику ![]()
![]()
![]() ,
, ![]() . Доведіть, що медіани трикутника
. Доведіть, що медіани трикутника ![]() і
і ![]() перпендикулярні.
перпендикулярні.
369. Числа ![]() ,
, ![]() і
і ![]() є довжинами медіан деякого трикутника. Доведіть, що коли виконується рівність
є довжинами медіан деякого трикутника. Доведіть, що коли виконується рівність ![]() , то трикутник є прямокутним.
, то трикутник є прямокутним.
370. Медіани трикутника дорівнюють ![]() см,
см, ![]() см і
см і ![]() см. Доведіть, що трикутник прямокутний.
см. Доведіть, що трикутник прямокутний.
371. У трикутнику ![]() проведено медіани
проведено медіани ![]() і
і ![]() ;
; ![]() – точка перетину медіан. Доведіть, що площі трикутника
– точка перетину медіан. Доведіть, що площі трикутника ![]() і чотирикутника
і чотирикутника ![]() рівні.
рівні.
372. Нехай числа ![]() ,
, ![]() і
і ![]() є довжинами висот деякого трикутника і виконується рівність
є довжинами висот деякого трикутника і виконується рівність 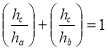 . Доведіть, що трикутник є прямокутним.
. Доведіть, що трикутник є прямокутним.
373. Усередині рівностороннього трикутника позначено довільну точку ![]() , що знаходиться на відстанях
, що знаходиться на відстанях ![]() ,
, ![]() і
і ![]() від сторін трикутника. Доведіть, що висота трикутника дорівнює
від сторін трикутника. Доведіть, що висота трикутника дорівнює ![]() .
.
374. З довільної точки ![]() катета
катета ![]() прямокутного трикутника
прямокутного трикутника ![]() опущено перпендикуляр
опущено перпендикуляр ![]() на гіпотенузу
на гіпотенузу ![]() . Доведіть, що
. Доведіть, що ![]() .
.
375. У гострокутному трикутнику ![]() відрізок
відрізок ![]() є висотою. З точки
є висотою. З точки ![]() на сторони
на сторони ![]() і
і ![]() опущено перпендикуляри
опущено перпендикуляри ![]() і
і ![]() відповідно. Доведіть, що чотирикутник
відповідно. Доведіть, що чотирикутник ![]() – вписаний.
– вписаний.
376. Усередині трикутника ![]() обрано точку
обрано точку ![]() так, що площі трикутників
так, що площі трикутників ![]() ,
, ![]() ,
, ![]() рівні. Доведіть, що
рівні. Доведіть, що ![]() – точка перетину медіан трикутника
– точка перетину медіан трикутника ![]() .
.
377. У трикутнику ![]()
![]() ,
, ![]() . На стороні
. На стороні ![]() побудовано квадрат, точка
побудовано квадрат, точка ![]() – його центр, точки
– його центр, точки ![]() і
і ![]() лежать по різні сторони від прямої
лежать по різні сторони від прямої ![]() . Доведіть, що
. Доведіть, що ![]() .
.
378. Точка ![]() – середина сторони
– середина сторони ![]() трикутника
трикутника ![]() . На відрізку
. На відрізку ![]() позначили точку
позначили точку ![]() . Через точку
. Через точку ![]() проведено відрізок
проведено відрізок ![]() , паралельний
, паралельний ![]() (
(![]() належить стороні
належить стороні ![]() ). Доведіть, що відрізок
). Доведіть, що відрізок ![]() ділить трикутник
ділить трикутник ![]() на дві рівновеликі фігури.
на дві рівновеликі фігури.
379. У трикутнику ![]() бісектриси
бісектриси ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
380. У трикутнику ![]() проведено медіани
проведено медіани ![]() і
і ![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що трикутник
. Доведіть, що трикутник ![]() – рівнобедрений.
– рівнобедрений.
381. У трикутнику ![]()
![]() ,
, ![]() . На стороні
. На стороні ![]() побудовано рівносторонній трикутник
побудовано рівносторонній трикутник ![]() , точки
, точки ![]() і
і ![]() лежать по різні сторони від прямої
лежать по різні сторони від прямої ![]() . Доведіть, що
. Доведіть, що ![]() .
.
382. Точка ![]() – середина сторони
– середина сторони ![]() трикутника
трикутника ![]() . На відрізках
. На відрізках ![]() і
і ![]() позначено відповідно точки
позначено відповідно точки ![]() і
і ![]() так, що відрізок
так, що відрізок ![]() розбиває трикутник
розбиває трикутник ![]() на дві рівновеликі частини. Доведіть, що
на дві рівновеликі частини. Доведіть, що ![]() .
.
383. На катеті ![]() прямокутного трикутника
прямокутного трикутника ![]() взято довільну точку
взято довільну точку ![]() . З точки
. З точки ![]() проведено перпендикуляр
проведено перпендикуляр ![]() до гіпотенузи
до гіпотенузи ![]() . Доведіть, що
. Доведіть, що ![]() .
.
384. У трикутнику ![]() бісектриси
бісектриси ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
385. У рівнобедреному трикутнику ![]()
![]() кут при вершині дорівнює
кут при вершині дорівнює ![]() . У цьому трикутнику проведено бісектриси
. У цьому трикутнику проведено бісектриси ![]() і
і ![]() . Доведіть, що
. Доведіть, що ![]() .
.
386. У трикутнику ![]() проведено медіани
проведено медіани ![]() і
і ![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що трикутник
. Доведіть, що трикутник ![]() – рівнобедрений.
– рівнобедрений.
Геометричні побудови у трикутнику
387. Побудуйте трикутник за двома сторонами і медіаною, проведеною до його третьої сторони.
388. Побудуйте трикутник за медіаною і двома кутами, на які ця медіана ділить кут трикутника.
389. На стороні ![]() гострокутного трикутника
гострокутного трикутника ![]() знайдіть таку точку, щоб відстань між її проекціями на дві інші сторони була найменшою.
знайдіть таку точку, щоб відстань між її проекціями на дві інші сторони була найменшою.
390. Дано дві точки ![]() і
і ![]() . Знайдіть геометричне місце точок
. Знайдіть геометричне місце точок ![]() таких, що медіана
таких, що медіана ![]() трикутника
трикутника ![]() дорівнює його стороні
дорівнює його стороні ![]() .
.
391. Дано дві точки ![]() і
і ![]() . Знайдіть геометричне місце точок
. Знайдіть геометричне місце точок ![]() таких, що висота
таких, що висота ![]() трикутника
трикутника ![]() вдвічі більша за його медіану
вдвічі більша за його медіану ![]() .
.
Площа трикутника
392. Дві сторони трикутника дорівнюють ![]() і
і ![]() , а його площа –
, а його площа – ![]() . Доведіть, що виконується нерівність
. Доведіть, що виконується нерівність ![]() .
.
393. Дві сторони трикутника дорівнюють ![]() і
і ![]() , а його площа –
, а його площа – ![]() . Доведіть, що виконується нерівність
. Доведіть, що виконується нерівність ![]() .
.
394. Доведіть, що площу ![]() прямокутного трикутника можна знайти за формулою
прямокутного трикутника можна знайти за формулою ![]() , де
, де ![]() – півпериметр трикутника,
– півпериметр трикутника, ![]() – довжина гіпотенузи.
– довжина гіпотенузи.
395. Доведіть, що площу ![]() прямокутного трикутника можна знайти за формулою
прямокутного трикутника можна знайти за формулою ![]() , де
, де ![]() – півпериметр трикутника,
– півпериметр трикутника, ![]() і
і ![]() – довжини катетів.
– довжини катетів.
396. У прямокутному трикутнику ![]()
![]() проведено медіану
проведено медіану ![]() . Відомо, що
. Відомо, що ![]() , а площа трикутника
, а площа трикутника ![]() дорівнює
дорівнює ![]() . Знайдіть медіану
. Знайдіть медіану ![]() .
.
397. У прямокутному трикутнику ![]()
![]() медіана
медіана ![]() , проведена до меншого катета, утворює з більшим катетом кут
, проведена до меншого катета, утворює з більшим катетом кут ![]() . Знайдіть площу трикутника
. Знайдіть площу трикутника ![]() , якщо
, якщо ![]() .
.
398. Точки ![]() ,
, ![]() ,
, ![]() належать сторонам
належать сторонам ![]() ,
, ![]() ,
, ![]() трикутника
трикутника ![]() відповідно. Відомо, що
відповідно. Відомо, що ![]() . Площа трикутника
. Площа трикутника ![]() дорівнює
дорівнює ![]() . Знайдіть площу трикутника
. Знайдіть площу трикутника ![]() .
.
399. Точки ![]() ,
, ![]() ,
, ![]() належать сторонам
належать сторонам ![]() ,
, ![]() ,
, ![]() трикутника
трикутника ![]() відповідно. Відомо, що
відповідно. Відомо, що ![]() . Площа трикутника
. Площа трикутника ![]() дорівнює
дорівнює ![]() . Знайдіть площу трикутника
. Знайдіть площу трикутника ![]() .
.
400. Два трикутники ![]() і
і ![]() розташовані так, що точка
розташовані так, що точка ![]() – середина відрізка
– середина відрізка ![]() , точка
, точка ![]() – середина відрізка
– середина відрізка ![]() , точка
, точка ![]() – середина відрізка
– середина відрізка ![]() . Знайдіть площу трикутника
. Знайдіть площу трикутника ![]() , якщо площа трикутника
, якщо площа трикутника ![]() дорівнює
дорівнює ![]() .
.
401. У трикутнику ![]() проведено медіану
проведено медіану ![]() . Через точку
. Через точку ![]() проведено відрізок
проведено відрізок ![]() , який дорівнює відрізку
, який дорівнює відрізку ![]() і паралельний йому. Знайдіть площу чотирикутника
і паралельний йому. Знайдіть площу чотирикутника ![]() , якщо площа трикутника
, якщо площа трикутника ![]() дорівнює
дорівнює ![]() .
.
402. Через точку перетину медіан трикутника ![]() проведено відрізок
проведено відрізок ![]() паралельно стороні
паралельно стороні ![]() . Знайдіть площу чотирикутника
. Знайдіть площу чотирикутника ![]() , якщо
, якщо ![]() і площа трикутника
і площа трикутника ![]() дорівнює
дорівнює ![]() .
.
403. Знайдіть площу трикутника, якщо дві його сторони дорівнюють ![]() см і
см і ![]() см, а медіана, яка проведена до третьої сторони, дорівнює
см, а медіана, яка проведена до третьої сторони, дорівнює ![]() см.
см.
404. Сторони трикутника дорівнюють ![]() см,
см, ![]() см і
см і ![]() см. Обчисліть площі кожної із шести трикутників, на які розбивається даний трикутник його медіанами.
см. Обчисліть площі кожної із шести трикутників, на які розбивається даний трикутник його медіанами.
405. Сторона трикутника дорівнює ![]() см, а медіани, проведені до двох інших сторін, –
см, а медіани, проведені до двох інших сторін, – ![]() см і
см і ![]() см. Знайдіть площу трикутника.
см. Знайдіть площу трикутника.
406. У трикутнику ![]() проведено медіани
проведено медіани ![]() і
і ![]() ; точка
; точка ![]() – точка перетину медіан. Доведіть, що площі трикутника
– точка перетину медіан. Доведіть, що площі трикутника ![]() і чотирикутника
і чотирикутника ![]() рівні.
рівні.
407. Рівносторонній трикутник, площа якого ![]() , повернули навколо однієї з його вершин на
, повернули навколо однієї з його вершин на ![]() . Знайдіть площу спільної частини даного і одержаного трикутників.
. Знайдіть площу спільної частини даного і одержаного трикутників.
408. У рівносторонній трикутник ![]() вписано інший рівносторонній трикутник
вписано інший рівносторонній трикутник ![]() , вершини якого лежать на сторонах першого трикутника і ділять кожну з них у відношенні
, вершини якого лежать на сторонах першого трикутника і ділять кожну з них у відношенні ![]() . Знайдіть відношення площ трикутників
. Знайдіть відношення площ трикутників ![]() і
і ![]() .
.
409. Площа рівностороннього трикутника, побудованого на гіпотенузі прямокутного трикутника, вдвічі більша за площу цього прямокутного трикутника. Знайдіть відношення катетів прямокутного трикутника.
410. Пряма, паралельна стороні ![]() трикутника
трикутника ![]() , перетинає сторони
, перетинає сторони ![]() та
та ![]() в точках
в точках ![]() і
і ![]() . Ці точки з’єднані з довільною точкою
. Ці точки з’єднані з довільною точкою ![]() , що належить стороні
, що належить стороні ![]() . Знайдіть площу чотирикутника
. Знайдіть площу чотирикутника ![]() , коли відомо, що площі трикутників
, коли відомо, що площі трикутників ![]() і
і ![]() відповідно дорівнюють
відповідно дорівнюють ![]() і
і ![]() .
.
Чотирикутник
411. Доведіть, що в опуклому чотирикутнику сума діагоналей менша від периметра.
412. Доведіть, що в опуклому чотирикутнику сума діагоналей більша за півпериметр.
413. Відрізок, який сполучає середини двох протилежних сторін опуклого чотирикутника, ділить його на два рівновеликих чотирикутники. Доведіть, що ці сторони паралельні.
414. Доведіть, що відрізки, які сполучають середини протилежних сторін опуклого чотирикутника, і відрізок, який сполучає середини діагоналей, перетинаються в одній точці.
415. Площа опуклого чотирикутника дорівнює половині добутку його діагоналей. Доведіть, що відрізки, які сполучають середини протилежних сторін чотирикутника, рівні.
416. Діагональ опуклого чотирикутника ділить його на два рівновеликих трикутники. Доведіть, що ця діагональ ділить навпіл відрізок, який з’єднує середини двох протилежних сторін чотирикутника.
417. Діагоналі опуклого чотирикутника взаємно перпендикулярні. Доведіть, що відрізки, які сполучають середини протилежних сторін чотирикутника, рівні.
418. Діагональ опуклого чотирикутника ділить навпіл відрізок, який з’єднує середини двох його протилежних сторін. Доведіть, що ця діагональ ділить чотирикутник на два рівновеликих трикутника.
419. В опуклому чотирикутнику відрізки, які сполучають середини протилежних сторін, рівні. Доведіть, що діагоналі чотирикутника перпендикулярні.
420. Діагоналі опуклого чотирикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Відомо, що
. Відомо, що ![]() см2,
см2, ![]() см2,
см2, ![]() см2. Знайдіть площі трикутників
см2. Знайдіть площі трикутників ![]() і
і ![]() .
.
421. Діагоналі опуклого чотирикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Відомо, що
. Відомо, що ![]() см2,
см2, ![]() см2,
см2, ![]() см2. Знайдіть площі трикутників
см2. Знайдіть площі трикутників ![]() і
і ![]() .
.
422. В опуклому чотирикутнику відрізки, які сполучають середини протилежних сторін, дорівнюють ![]() і
і ![]() , кут між ними дорівнює
, кут між ними дорівнює ![]() . Знайдіть діагоналі чотирикутника.
. Знайдіть діагоналі чотирикутника.
423. В опуклому чотирикутнику ![]() відомо, що
відомо, що ![]() . Бісектриса кута
. Бісектриса кута ![]() перетинає сторону
перетинає сторону ![]() у точці
у точці ![]() . На стороні
. На стороні ![]() позначено точку
позначено точку ![]() так, що
так, що ![]() . Доведіть, що
. Доведіть, що ![]() .
.
424. Діагоналі опуклого чотирикутника дорівнюють ![]() і
і ![]() , кут між ними дорівнює
, кут між ними дорівнює ![]() . Знайдіть відрізки, які сполучають середини протилежних сторін чотирикутника.
. Знайдіть відрізки, які сполучають середини протилежних сторін чотирикутника.
425. Довільний чотирикутник поділено діагоналями на чотири трикутники. Площі трьох з них дорівнюють ![]() дм2,
дм2, ![]() дм2 і
дм2 і ![]() дм2, і кожна із цих площ менша за площу четвертого трикутника. Знайдіть площу даного чотирикутника.
дм2, і кожна із цих площ менша за площу четвертого трикутника. Знайдіть площу даного чотирикутника.
426. Діагоналі опуклого чотирикутника розбивають його на чотири трикутники. Площі трьох з них дорівнюють ![]() ,
, ![]() ,
, ![]() . Знайдіть площу четвертого трикутника.
. Знайдіть площу четвертого трикутника.
427. В опуклому чотирикутнику ![]() діагональ
діагональ ![]() є бісектрисою кута
є бісектрисою кута ![]() . Відомо, що
. Відомо, що ![]() см,
см, ![]() см,
см, ![]() см,
см, ![]() см. Знайдіть кут
см. Знайдіть кут ![]() .
.
428. Діагоналі опуклого чотирикутника дорівнюють ![]() і
і ![]() . Відрізки, що з’єднують середини протилежних сторін, рівні. Знайдіть площу чотирикутника.
. Відрізки, що з’єднують середини протилежних сторін, рівні. Знайдіть площу чотирикутника.
429. В опуклому чотирикутнику ![]() діагональ
діагональ ![]() є бісектрисою кута
є бісектрисою кута ![]() . Відомо, що
. Відомо, що ![]() см,
см, ![]() см,
см, ![]() см,
см, ![]() см. Знайдіть кут
см. Знайдіть кут ![]() .
.
Паралелограм
430. На стороні ![]() і діагоналі
і діагоналі ![]() паралелограма
паралелограма ![]() позначено відповідно точки
позначено відповідно точки ![]() і
і ![]() так, що
так, що ![]() ,
, ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() і
і ![]() лежать на одній прямій.
лежать на одній прямій.
431. На стороні ![]() і діагоналі
і діагоналі ![]() паралелограма
паралелограма ![]() позначили відповідно точки
позначили відповідно точки ![]() і
і ![]() так, що
так, що ![]() ,
, ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() ,
, ![]() лежать на одній прямій.
лежать на одній прямій.
432. У паралелограмі ![]() на сторонах
на сторонах ![]() і
і ![]() позначено відповідно точки
позначено відповідно точки ![]() і
і ![]() так, що
так, що ![]() і
і ![]() . Відрізки
. Відрізки ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() . Знайдіть відношення
. Знайдіть відношення ![]() .
.
433. У паралелограмі ![]() на сторонах
на сторонах ![]() і
і ![]() позначено відповідно точки
позначено відповідно точки ![]() і
і ![]() так, що
так, що ![]() і
і ![]() . Відрізки
. Відрізки ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() . Знайдіть відношення
. Знайдіть відношення ![]() .
.
434. На протилежних сторонах паралелограма як на сторонах поза ним побудовано квадрати. Доведіть, що пряма, яка проходить через центри квадратів, проходить також через точку перетину діагоналей паралелограма.
435. На стороні ![]() і діагоналі
і діагоналі ![]() паралелограма
паралелограма ![]() позначено точки
позначено точки ![]() і
і ![]() відповідно так, що
відповідно так, що ![]() ,
, ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() і
і ![]() лежать на одній прямій.
лежать на одній прямій.
436. На сторонах ![]() і
і ![]() паралелограма
паралелограма ![]() побудовано поза ним рівносторонні трикутники
побудовано поза ним рівносторонні трикутники ![]() і
і ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() і
і ![]() , де
, де ![]() – точка перетину діагоналей паралелограма, лежать на одній прямій.
– точка перетину діагоналей паралелограма, лежать на одній прямій.
437. Точки ![]() і
і ![]() – середини сторін
– середини сторін ![]() і
і ![]() паралелограма
паралелограма ![]() відповідно. Доведіть, що відрізки
відповідно. Доведіть, що відрізки ![]() і
і ![]() ділять діагональ
ділять діагональ ![]() на три частини.
на три частини.
438. Кожна діагональ чотирикутника ділить його на два рівновеликих трикутники. Доведіть, що цей чотирикутник – паралелограм.
439. У паралелограмі ![]()
![]() , точка
, точка ![]() – середина сторони
– середина сторони ![]() . Знайдіть сторони паралелограма, якщо
. Знайдіть сторони паралелограма, якщо ![]() см,
см, ![]() см.
см.
440. Сторони паралелограма дорівнюють ![]() і
і ![]() , а діагоналі –
, а діагоналі – ![]() і
і ![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що гострий кут паралелограма дорівнює
. Доведіть, що гострий кут паралелограма дорівнює ![]() .
.
441. ![]() – паралелограм. Точки
– паралелограм. Точки ![]() і
і ![]() – середини сторін
– середини сторін ![]() і
і ![]() відповідно. Через вершину
відповідно. Через вершину ![]() паралелограма проведено прямі
паралелограма проведено прямі ![]() та
та ![]() . Доведіть, що ці прямі ділять діагональ
. Доведіть, що ці прямі ділять діагональ ![]() паралелограма на три рівні частини.
паралелограма на три рівні частини.
442. У паралелограмі проведено бісектриси всіх його кутів. Доведіть, що чотирикутник, утворений точками перетину бісектрис, є прямокутником, діагональ якого дорівнює різниці суміжних сторін паралелограма.
443. Два паралелограми ![]() і
і ![]() розташовані так, що точка
розташовані так, що точка ![]() – середина відрізка
– середина відрізка ![]() , точка
, точка ![]() – середина відрізка
– середина відрізка ![]() , точка
, точка ![]() – середина відрізка
– середина відрізка ![]() , точка
, точка ![]() – середина відрізка
– середина відрізка ![]() . Знайдіть площу паралелограма
. Знайдіть площу паралелограма ![]() , якщо площа паралелограма
, якщо площа паралелограма ![]() дорівнює
дорівнює ![]() .
.
Прямокутник і квадрат
444. Серединний перпендикуляр діагоналі ![]() прямокутника
прямокутника ![]() перетинає сторону
перетинає сторону ![]() і утворює з нею кут, який дорівнює куту між діагоналями. Знайдіть цей кут.
і утворює з нею кут, який дорівнює куту між діагоналями. Знайдіть цей кут.
445. Серединний перпендикуляр діагоналі ![]() прямокутника
прямокутника ![]() перетинає сторону
перетинає сторону ![]() у точці
у точці ![]() так, що
так, що ![]() . Знайдіть кути, на які діагональ прямокутника ділить його кут.
. Знайдіть кути, на які діагональ прямокутника ділить його кут.
446. Усередині прямокутника ![]() позначено точку
позначено точку ![]() . Доведіть, що існує опуклий чотирикутник, діагоналі якого перпендикулярні і дорівнюють
. Доведіть, що існує опуклий чотирикутник, діагоналі якого перпендикулярні і дорівнюють ![]() і
і ![]() , а сторони дорівнюють
, а сторони дорівнюють ![]() ,
, ![]() ,
, ![]() і
і ![]() .
.
447. На сторонах ![]() і
і ![]() квадрата
квадрата ![]() позначено точки
позначено точки ![]() і
і ![]() відповідно так, що
відповідно так, що ![]() . Знайдіть кут
. Знайдіть кут ![]() , де точка
, де точка ![]() – центр квадрата.
– центр квадрата.
448. Точка ![]() – середина сторони
– середина сторони ![]() квадрата
квадрата ![]() , а точка
, а точка ![]() ділить його діагональ
ділить його діагональ ![]() у відношенні
у відношенні ![]() . Доведіть, що кут
. Доведіть, що кут ![]() прямий.
прямий.
449. Вершина ![]() квадрата
квадрата ![]() є центром повороту на кут
є центром повороту на кут ![]() . Знайдіть відрізок
. Знайдіть відрізок ![]() , де точка
, де точка ![]() – образ точки
– образ точки ![]() при вказаному повороті, якщо
при вказаному повороті, якщо ![]() см.
см.
450. Сторона квадрата дорівнює ![]() . Цей квадрат повернули навколо однієї з його вершин на
. Цей квадрат повернули навколо однієї з його вершин на ![]() . Знайдіть площу спільної частини і одержаного квадратів.
. Знайдіть площу спільної частини і одержаного квадратів.
Трапеція
451. Діагоналі трапеції перпендикулярні. Доведіть, що середня лінія трапеції дорівнює відрізку, який сполучає середини основ.
452. Доведіть, що середини основ трапеції і точка перетину її діагоналей лежать на одній прямій.
453. Середня лінія трапеції дорівнює відрізку, який сполучає середини основ. Доведіть, що діагоналі цієї трапеції перпендикулярні.
454. Доведіть, що середини основ трапеції і точка перетину продовжень її бічних сторін лежать на одній прямій.
455. Довжини основ трапеції дорівнюють ![]() і
і ![]()
![]() . Знайдіть довжину відрізка прямої, паралельної основам трапеції, що міститься між її бічними сторонами і ділить трапецію на дві рівновеликі фігури.
. Знайдіть довжину відрізка прямої, паралельної основам трапеції, що міститься між її бічними сторонами і ділить трапецію на дві рівновеликі фігури.
456. Діагоналі рівнобічної трапеції взаємно перпендикулярні, а її висота дорівнює ![]() . Знайдіть площу цієї трапеції.
. Знайдіть площу цієї трапеції.
457. Діагоналі трапеції розбивають її на чотири трикутники. Площі трикутників, що прилягають до основ трапеції, дорівнюють ![]() і
і ![]() . Доведіть, що площа трапеції дорівнює
. Доведіть, що площа трапеції дорівнює ![]() .
.
458. Доведіть, що точка перетину діагоналей трапеції належить прямій, що проходить через середини основ трапеції.
459. Через точку перетину діагоналей трапеції паралельно її основам проведено пряму, яка перетинає бічні сторони в точках ![]() і
і ![]() . Знайдіть довжину відрізка
. Знайдіть довжину відрізка ![]() , якщо основи трапеції дорівнюють
, якщо основи трапеції дорівнюють ![]() см і
см і ![]() см.
см.
460. Діагоналі рівнобічної трапеції взаємно перпендикулярні, а висота дорівнює ![]() . Знайдіть площу цієї трапеції.
. Знайдіть площу цієї трапеції.
461. Через точку перетину діагоналей трапеції паралельно основам проведено пряму, що перетинає бічні сторони в точках ![]() і
і ![]() . Знайдіть довжину відрізка
. Знайдіть довжину відрізка ![]() , якщо основи трапеції дорівнюють
, якщо основи трапеції дорівнюють ![]() см і
см і ![]() см.
см.
462. Доведіть, що точка перетину діагоналей трапеції належить прямій, що проходить через середини основ трапеції.
463. Діагоналі трапеції розбивають її на чотири трикутники. Площі трикутників, які прилягають до основ трапеції, дорівнюють ![]() і
і ![]() . Доведіть, що площа трапеції дорівнює
. Доведіть, що площа трапеції дорівнює ![]() .
.
464. Довжина середньої лінії трапеції дорівнює ![]() см, а довжина відрізка, який сполучає середини основ, –
см, а довжина відрізка, який сполучає середини основ, – ![]() см. Кути при більшій основі дорівнюють
см. Кути при більшій основі дорівнюють ![]() і
і ![]() . Знайдіть основи трапеції.
. Знайдіть основи трапеції.
465. Доведіть, що середини основ трапеції і точка перетину її діагоналей лежать на одній прямій.
466. Діагональ ![]() трапеції
трапеції ![]() дорівнює сумі основ
дорівнює сумі основ ![]() і
і ![]() . Діагоналі
. Діагоналі ![]() і
і ![]() перетинаються в точці
перетинаються в точці ![]() ,
, ![]() . Доведіть, що трапеція
. Доведіть, що трапеція ![]() – рівнобічна.
– рівнобічна.
467. Середня лінія трапеції дорівнює відрізку, який сполучає середини основ. Доведіть, що діагоналі цієї трапеції перпендикулярні.
468. Діагоналі трапеції перпендикулярні. Доведіть, що середня лінія трапеції дорівнює відрізку, який сполучає середини основ.
469. Доведіть, що середини основ трапеції і точка перетину її бічних сторін лежать на одній прямій.
470. Доведіть, що для будь-якої трапеції площа трикутника, основою якого є одна з непаралельних сторін трапеції, а вершиною – середина протилежної сторони, дорівнює половині площі трапеції.
471. Основи трапеції дорівнюють ![]() см і
см і ![]() см. Пряма, паралельна основі трапеції, проходить через точку перетину діагоналей. Знайдіть довжину відрізка цієї прямої, що міститься між бічними сторонами трапеції.
см. Пряма, паралельна основі трапеції, проходить через точку перетину діагоналей. Знайдіть довжину відрізка цієї прямої, що міститься між бічними сторонами трапеції.
472. Кути при основі трапеції дорівнюють ![]() і
і ![]() , а довжина відрізка, який з’єднує середини основ, –
, а довжина відрізка, який з’єднує середини основ, – ![]() см. Знайдіть довжини основ трапеції, якщо довжина її середньої лінії дорівнює
см. Знайдіть довжини основ трапеції, якщо довжина її середньої лінії дорівнює ![]() см.
см.
473. У прямокутній трапеції відношення довжин основ дорівнює ![]() , а відношення довжин діагоналей дорівнює
, а відношення довжин діагоналей дорівнює ![]() . Знайдіть гострий кут трапеції.
. Знайдіть гострий кут трапеції.
474. Середня лінія трапеції ділить площу трапеції у відношенні ![]() . Знайдіть основи трапеції, якщо її середня лінія дорівнює
. Знайдіть основи трапеції, якщо її середня лінія дорівнює ![]() см.
см.
475. У рівнобічній трапеції ![]()
![]() відстань від вершини
відстань від вершини ![]() до прямої
до прямої ![]() дорівнює довжині бічної сторони, а основи трапеції
дорівнює довжині бічної сторони, а основи трапеції ![]() і
і ![]() відносяться як
відносяться як ![]() . Знайдіть кути трапеції.
. Знайдіть кути трапеції.
476. У трапеції проведено діагоналі. Площі трикутників, які прилягають до її основ, дорівнюють ![]() і
і ![]() . Доведіть, що площа цієї трапеції дорівнює
. Доведіть, що площа цієї трапеції дорівнює ![]() .
.
477. Основи трапеції дорівнюють ![]() та
та ![]() . Відрізок, кінці якого лежать на бічних сторонах трапеції, паралельний основам і ділить трапецію на дві рівновеликі частини. Знайдіть довжину цього відрізка.
. Відрізок, кінці якого лежать на бічних сторонах трапеції, паралельний основам і ділить трапецію на дві рівновеликі частини. Знайдіть довжину цього відрізка.
478. Основи рівнобічної трапеції дорівнюють ![]() см і
см і ![]() см, а її діагоналі перпендикулярні до бічних сторін. Знайдіть площу цієї трапеції.
см, а її діагоналі перпендикулярні до бічних сторін. Знайдіть площу цієї трапеції.
479. У трапеції ![]() діагоналі
діагоналі ![]() і
і ![]() перпендикулярні. Знайдіть площу трапеції, якщо
перпендикулярні. Знайдіть площу трапеції, якщо ![]() см, а висота трапеції дорівнює
см, а висота трапеції дорівнює ![]() см.
см.
480. Точки ![]() і
і ![]() – середини сторін
– середини сторін ![]() і
і ![]() опуклого чотирикутника
опуклого чотирикутника ![]()
![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що даний чотирикутник – трапеція.
. Доведіть, що даний чотирикутник – трапеція.
481. На відрізку, що з’єднує середини основ трапеції, взято точку, яку сполучено з усіма вершинами трапеції. Доведіть, що трикутники, прилеглі до бічних сторін трапеції, рівновеликі.
482. У трапеції ![]() діагоналі
діагоналі ![]() і
і ![]() перпендикулярні. Знайдіть площу трапеції, якщо
перпендикулярні. Знайдіть площу трапеції, якщо ![]() см, а середня лінія трапеції дорівнює
см, а середня лінія трапеції дорівнює ![]() см.
см.
483. Точки ![]() і
і ![]() – середини діагоналей
– середини діагоналей ![]() і
і ![]() опуклого чотирикутника
опуклого чотирикутника ![]()
![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що даний чотирикутник – трапеція.
. Доведіть, що даний чотирикутник – трапеція.
Коло та його елементи
484. На катеті ![]() прямокутного трикутника
прямокутного трикутника ![]() як на діаметрі побудовано коло, яке перетинає гіпотенузу
як на діаметрі побудовано коло, яке перетинає гіпотенузу ![]() у точці
у точці ![]() . Через точку
. Через точку ![]() проведено дотичну до цього кола, яка перетинає катет
проведено дотичну до цього кола, яка перетинає катет ![]() у точці
у точці ![]() . Доведіть, що трикутник
. Доведіть, що трикутник ![]() – рівнобедрений.
– рівнобедрений.
485. До двох кіл, які перетинаються в точках ![]() і
і ![]() , проведено спільну дотичну,
, проведено спільну дотичну, ![]() і
і ![]() – точки дотику. Доведіть, що
– точки дотику. Доведіть, що ![]() .
.
486. Два кола перетинаються в точках ![]() і
і ![]() . Через точку
. Через точку ![]() проведено пряму, яка перетинає кола в точках
проведено пряму, яка перетинає кола в точках ![]() і
і ![]() . У точках
. У точках ![]() і
і ![]() до даних кіл проведено дотичні, які перетинаються в точці
до даних кіл проведено дотичні, які перетинаються в точці ![]() . Доведіть, що
. Доведіть, що ![]() .
.
487. У колі проведено три хорди ![]() см,
см, ![]() см,
см, ![]() см. Відомо, що
см. Відомо, що ![]() . Знайдіть радіус кола.
. Знайдіть радіус кола.
488. Дано квадрат, дві вершини якого лежать на колі радіуса ![]() , а дві інші – на дотичній до цього кола. Знайдіть площу квадрата.
, а дві інші – на дотичній до цього кола. Знайдіть площу квадрата.
489. Через точку ![]() діаметра кола проведено хорду
діаметра кола проведено хорду ![]() , що утворює з діаметром кут
, що утворює з діаметром кут ![]() . Знайдіть довжину кола, якщо
. Знайдіть довжину кола, якщо ![]() см,
см, ![]() см.
см.
490. У колі проведено дві перпендикулярні хорди ![]() і
і ![]() , які перетинаються в точці
, які перетинаються в точці ![]() . Доведіть, що пряма, яка містить медіану
. Доведіть, що пряма, яка містить медіану ![]() трикутника
трикутника ![]() , містить також висоту трикутника
, містить також висоту трикутника ![]() .
.
491. На хорді ![]() кола позначено точку
кола позначено точку ![]() . Доведіть, що
. Доведіть, що ![]() , де
, де ![]() – радіус кола,
– радіус кола, ![]() – відстань від точки
– відстань від точки ![]() до центра кола.
до центра кола.
492. У колі проведено дві перпендикулярні хорди ![]() і
і ![]() , які перетинаються в точці
, які перетинаються в точці ![]() . Доведіть, що пряма, яка містить висоту трикутника
. Доведіть, що пряма, яка містить висоту трикутника ![]() , містить також медіану трикутника
, містить також медіану трикутника ![]() .
.
493. Через точку ![]() поза колом проведено пряму, яка перетинає дане коло в точках
поза колом проведено пряму, яка перетинає дане коло в точках ![]() і
і ![]() . Доведіть, що
. Доведіть, що ![]() , де
, де ![]() – радіус кола,
– радіус кола, ![]() – відстань від точки
– відстань від точки ![]() до центра кола.
до центра кола.
494. Дано два концентричних кола. Доведіть, що сума квадратів відстаней від точки одного кола до кінців діаметра іншого кола не залежить ні від обраної точки, ні від обраного діаметра.
495. На стороні ![]() трикутника
трикутника ![]() як на діаметрі побудовано коло, яке перетинає сторони
як на діаметрі побудовано коло, яке перетинає сторони ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Знайдіть градусну міру кута
відповідно. Знайдіть градусну міру кута ![]() , якщо площі трикутників
, якщо площі трикутників ![]() і
і ![]() відносяться як
відносяться як ![]() .
.
496. Два кола, радіуси яких дорівнюють ![]() і
і ![]() , лежать в одній площині та дотикаються одне одного. Знайдіть радіус кола, яке дотикається до заданих кіл і їх спільної зовнішньої дотичної.
, лежать в одній площині та дотикаються одне одного. Знайдіть радіус кола, яке дотикається до заданих кіл і їх спільної зовнішньої дотичної.
497. Три кола, радіуси яких дорівнюють ![]() дм,
дм, ![]() дм і
дм і ![]() дм, лежать в одній площині та попарно дотикається між собою. Знайдіть площу фігури, яка обмежена меншими дугами цих кіл.
дм, лежать в одній площині та попарно дотикається між собою. Знайдіть площу фігури, яка обмежена меншими дугами цих кіл.
498. Два кола перетинаються в точках ![]() і
і ![]() . Через точку
. Через точку ![]() , яка належить відрізку
, яка належить відрізку ![]() , проведено хорду
, проведено хорду ![]() першого кола і хорду
першого кола і хорду ![]() другого кола. Доведіть, що точки
другого кола. Доведіть, що точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() лежать на одному колі.
лежать на одному колі.
499. Відрізок ![]() є діаметром кола, а точка
є діаметром кола, а точка ![]() лежить поза цим колом. Відрізки
лежить поза цим колом. Відрізки ![]() і
і ![]() перетинаються з колом у точках
перетинаються з колом у точках ![]() і
і ![]() відповідно. Знайдіть кут
відповідно. Знайдіть кут ![]() , якщо площі трикутників
, якщо площі трикутників ![]() і
і ![]() відносяться як
відносяться як ![]() .
.
500. На діаметрі ![]() кола з центром у точці
кола з центром у точці ![]() взято точки
взято точки ![]() і
і ![]() так, що
так, що ![]() . Нехай
. Нехай ![]() – довільна точка даного кола. Доведіть, що сума
– довільна точка даного кола. Доведіть, що сума ![]() не залежить від вибору точки
не залежить від вибору точки ![]() .
.
501. Відомо, що ![]() – точка перетину відрізків
– точка перетину відрізків ![]() і
і ![]() ,
, ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() ,
, ![]() і
і ![]() належать одному колу.
належать одному колу.
502. У колі, радіус якого дорівнює ![]() , проведено дві хорди
, проведено дві хорди ![]() і
і ![]() , які перетинаються під прямим кутом. Доведіть, що
, які перетинаються під прямим кутом. Доведіть, що ![]() .
.
503. З точки ![]() , що рухається по колу, опущено перпендикуляри на фіксовані діаметри
, що рухається по колу, опущено перпендикуляри на фіксовані діаметри ![]() і
і ![]() . Доведіть, що довжина відрізка, який з’єднує основи перпендикулярів, не залежить від положення точки
. Доведіть, що довжина відрізка, який з’єднує основи перпендикулярів, не залежить від положення точки ![]() .
.
504. У трикутнику ![]()
![]() на катеті
на катеті ![]() як на діаметрі побудовано коло, що перетинає гіпотенузу
як на діаметрі побудовано коло, що перетинає гіпотенузу ![]() у точці
у точці ![]() . Через точку
. Через точку ![]() проведено дотичну, яка перетинає катет
проведено дотичну, яка перетинає катет ![]() у точці
у точці ![]() . Доведіть, що
. Доведіть, що ![]() .
.
505. Два кола перетинаються в точках ![]() і
і ![]() . Через точку
. Через точку ![]() проведено діаметри
проведено діаметри ![]() і
і ![]() . Доведіть, що точки
. Доведіть, що точки ![]() ,
, ![]() і
і ![]() лежать на одній прямій. Розгляньте випадки розташування центрів кіл в одній і різних півплощинах відносно прямої
лежать на одній прямій. Розгляньте випадки розташування центрів кіл в одній і різних півплощинах відносно прямої ![]() .
.
506. Коло, побудоване на більшій основі трапеції як на діаметрі, дотикається до меншої основи і перетинає бічні сторони та ділить їх навпіл. Знайдіть меншу основу трапеції, якщо радіус кола дорівнює ![]() .
.
507. Коло, побудоване на стороні ![]() трикутника
трикутника ![]() як на діаметрі, перетинає сторони
як на діаметрі, перетинає сторони ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Знайдіть відношення площ трикутників
відповідно. Знайдіть відношення площ трикутників ![]() і
і ![]() , якщо
, якщо ![]() .
.
508. Два кола перетинаються в точках ![]() і
і ![]() . Через точку
. Через точку ![]() проведено січну, яка перетинає кола в точках
проведено січну, яка перетинає кола в точках ![]() і
і ![]() . Доведіть, що величина кута
. Доведіть, що величина кута ![]() є сталою для будь-якої січної, яка проходить через точку
є сталою для будь-якої січної, яка проходить через точку ![]() . Розгляньте випадки розташування точок
. Розгляньте випадки розташування точок ![]() і
і ![]() в одній і різних півплощинах відносно прямої
в одній і різних півплощинах відносно прямої ![]() .
.
509. Коло, побудоване на більшій основі трапеції як на діаметрі, дотикається до меншої основи, перетинає бічні сторони і ділить їх навпіл. Знайдіть бічну сторону трапеції, якщо радіус кола дорівнює ![]() .
.
Вписаний та описаний трикутник
510. Доведіть, що точки, симетричні ортоцентру трикутника відносно прямих, які містять його сторони, лежать на описаному колі цього трикутника.
511. Відрізок ![]() – висота гострокутного трикутника
– висота гострокутного трикутника ![]() . Доведіть, що
. Доведіть, що ![]() , де точка
, де точка ![]() – центр описаного кола трикутника
– центр описаного кола трикутника ![]() .
.
512. До кола, вписаного в трикутник, проведено три дотичні, паралельні сторонам трикутника. Ці дотичні відтинають від даного трикутника три трикутники, радіуси описаних кіл яких дорівнюють ![]() ,
, ![]() ,
, ![]() . Знайдіть радіус описаного кола даного трикутника.
. Знайдіть радіус описаного кола даного трикутника.
513. Центри вписаного і описаного кіл трикутника ![]() лежать по різні сторони від прямої
лежать по різні сторони від прямої ![]() . Сторона
. Сторона ![]() дорівнює радіусу описаного кола. Чому дорівнює кут
дорівнює радіусу описаного кола. Чому дорівнює кут ![]() , де точка
, де точка ![]() – центр вписаного кола?
– центр вписаного кола?
514. Точка ![]() – ортоцентр трикутника
– ортоцентр трикутника ![]() . Радіус кола, описаного навколо трикутника
. Радіус кола, описаного навколо трикутника ![]() , дорівнює
, дорівнює ![]() . Доведіть, що
. Доведіть, що ![]() .
.
515. Доведіть, що описане коло трикутника ![]() , бісектриса кута
, бісектриса кута ![]() і серединний перпендикуляр сторони
і серединний перпендикуляр сторони ![]() проходять через одну точку.
проходять через одну точку.
516. Через точку ![]() до кола, описаного навколо трикутника
до кола, описаного навколо трикутника ![]() , проведено дотичну, яка перетинає пряму
, проведено дотичну, яка перетинає пряму ![]() у точці
у точці ![]() . Відрізок
. Відрізок ![]() – бісектриса трикутника
– бісектриса трикутника ![]() . Доведіть, що
. Доведіть, що ![]() .
.
517. У рівнобедрений трикутник з основою ![]() см вписано коло, а до нього проведено три дотичні так, що вони відтинають від даного трикутника три трикутники по одному біля кожної вершини. Сума периметрів трьох утворених трикутників дорівнює
см вписано коло, а до нього проведено три дотичні так, що вони відтинають від даного трикутника три трикутники по одному біля кожної вершини. Сума периметрів трьох утворених трикутників дорівнює ![]() см. Знайдіть бічну сторону даного трикутника.
см. Знайдіть бічну сторону даного трикутника.
518. Висоти гострокутного трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Доведіть, що радіуси кіл, описаних навколо трикутників
. Доведіть, що радіуси кіл, описаних навколо трикутників ![]() ,
, ![]() ,
, ![]() і
і ![]() , рівні.
, рівні.
519. У гострокутному трикутнику ![]() відрізок
відрізок ![]() є висотою. З точки
є висотою. З точки ![]() на сторони
на сторони ![]() і
і ![]() опущено перпендикуляри
опущено перпендикуляри ![]() і
і ![]() відповідно. Доведіть, що навколо чотирикутника
відповідно. Доведіть, що навколо чотирикутника ![]() можна описати коло.
можна описати коло.
520. У коло, радіус якого ![]() см, вписано рівнобедрений трикутник, бічна сторона якого вдвічі більша за основу. Знайдіть радіус кола, вписаного у цей трикутник.
см, вписано рівнобедрений трикутник, бічна сторона якого вдвічі більша за основу. Знайдіть радіус кола, вписаного у цей трикутник.
521. Дано трикутник ![]() , у якому
, у якому ![]() см,
см, ![]() см,
см, ![]() см.
см. ![]() – бісектриса трикутника,
– бісектриса трикутника, ![]() – центр кола, вписаного у трикутник. Знайдіть відношення
– центр кола, вписаного у трикутник. Знайдіть відношення ![]() .
.
522. У прямокутний трикутник вписано коло. Точка дотику ділить гіпотенузу у відношенні ![]() . Знайдіть сторони трикутника. Якщо центр вписаного кола віддалений від вершини прямого кута на відстань
. Знайдіть сторони трикутника. Якщо центр вписаного кола віддалений від вершини прямого кута на відстань ![]() см.
см.
523. У трикутник зі сторонами ![]() см,
см, ![]() см і
см і ![]() см вписано півколо так, що його центр лежить на середній за довжиною стороні трикутника і півколо дотикається двох інших сторін. Знайдіть довжину цього півкола.
см вписано півколо так, що його центр лежить на середній за довжиною стороні трикутника і півколо дотикається двох інших сторін. Знайдіть довжину цього півкола.
524. Півколо вписано в прямокутний трикутник так, що його центр лежить на гіпотенузі та ділить її на відрізки завдовжки ![]() см і
см і ![]() см. Знайдіть довжину дуги півкола, що міститься між точками його дотику з катетами.
см. Знайдіть довжину дуги півкола, що міститься між точками його дотику з катетами.
525. Знайдіть площу прямокутного трикутника, гіпотенуза якого ділиться точкою дотику вписаного кола на відрізки ![]() і
і ![]() .
.
526. Доведіть, що в трикутнику ![]() точка перетину бісектриси кута
точка перетину бісектриси кута ![]() із серединним перпендикуляром до сторони
із серединним перпендикуляром до сторони ![]() належить колу, описаному навколо трикутника
належить колу, описаному навколо трикутника ![]() .
.
527. Доведіть, що відстань від ортоцентра гострокутного трикутника до його вершини удвічі більша за відстань від центра описаного кола до сторони, яка протилежна цій вершині.
528. Бісектриса кута ![]() трикутника
трикутника ![]() перетинає описане навколо нього коло в точці
перетинає описане навколо нього коло в точці ![]() . Точка
. Точка ![]() – центр вписаного в трикутник
– центр вписаного в трикутник ![]() кола. Доведіть, що
кола. Доведіть, що ![]() .
.
529. Нехай ![]() ,
, ![]() ,
, ![]() – висоти трикутника,
– висоти трикутника, ![]() – радіус кола, вписаного у трикутник. Доведіть, що
– радіус кола, вписаного у трикутник. Доведіть, що ![]() .
.
530. Сторона трикутника дорівнює ![]() см, а сума двох інших сторін –
см, а сума двох інших сторін – ![]() см. Знайдіть косинус кута, що лежить проти даної сторони, якщо радіус кола, вписаного у трикутник, дорівнює
см. Знайдіть косинус кута, що лежить проти даної сторони, якщо радіус кола, вписаного у трикутник, дорівнює ![]() см.
см.
531. Прямі, які містять висоти гострокутного трикутника ![]() , перетинають його описане коло в точках
, перетинають його описане коло в точках ![]() ,
, ![]() і
і ![]() . Доведіть, що ортоцентр трикутника
. Доведіть, що ортоцентр трикутника ![]() є центром вписаного кола трикутника
є центром вписаного кола трикутника ![]() .
.
532. Прямі, які містять бісектриси трикутника ![]() , перетинають його описане коло в точках
, перетинають його описане коло в точках ![]() ,
, ![]() і
і ![]() . Доведіть, що центр вписаного кола трикутника
. Доведіть, що центр вписаного кола трикутника ![]() є ортоцентром трикутника
є ортоцентром трикутника ![]() .
.
533. Бісектриса кута ![]() трикутника
трикутника ![]() перетинає описане навколо нього коло в точці
перетинає описане навколо нього коло в точці ![]() . Точка
. Точка ![]() – центр вписаного кола трикутника
– центр вписаного кола трикутника ![]() . Доведіть, що
. Доведіть, що ![]() .
.
534. У гострокутному трикутнику ![]() точки
точки ![]() ,
, ![]() ,
, ![]() ,
, ![]() , де
, де ![]() – ортоцентр,
– ортоцентр, ![]() – центр описаного кола, лежать на одному колі. Знайдіть величину кута
– центр описаного кола, лежать на одному колі. Знайдіть величину кута ![]() .
.
535. Висота прямокутного трикутника ![]() , проведена до гіпотенузи, ділить його на два трикутники. Відстань між центрами кіл, вписаних у ці трикутники, дорівнює
, проведена до гіпотенузи, ділить його на два трикутники. Відстань між центрами кіл, вписаних у ці трикутники, дорівнює ![]() см. Знайдіть радіус кола, вписаного в трикутник
см. Знайдіть радіус кола, вписаного в трикутник ![]() .
.
536. У рівнобедреному трикутнику медіана, проведена до основи, дорівнює ![]() см, а медіана, проведена до бічної сторони, –
см, а медіана, проведена до бічної сторони, – ![]() см. Знайдіть радіус вписаного у цей трикутник кола.
см. Знайдіть радіус вписаного у цей трикутник кола.
537. Знайдіть гострі кути прямокутного трикутника, якщо відношення його радіусів описаного і вписаного кіл дорівнює ![]() .
.
538. У прямокутному трикутнику гострий кут дорівнює ![]() , а протилежний до нього катет дорівнює
, а протилежний до нього катет дорівнює ![]() см. З вершини другого гострого кута проведено бісектрису, яка ділить цей трикутник на два трикутники. Знайдіть відстань між центрами кіл, вписаних в одержані трикутники.
см. З вершини другого гострого кута проведено бісектрису, яка ділить цей трикутник на два трикутники. Знайдіть відстань між центрами кіл, вписаних в одержані трикутники.
539. Коло вписано в прямокутний трикутник. Точка дотику ділить менший з катетів у відношенні ![]() . Знайдіть кути цього трикутника.
. Знайдіть кути цього трикутника.
540. Кут при основі рівнобедреного трикутника дорівнює ![]() . Знайдіть відношення радіуса кола, вписаного в цей трикутник, до радіуса описаного кола.
. Знайдіть відношення радіуса кола, вписаного в цей трикутник, до радіуса описаного кола.
541. Сторони трикутника відносяться як ![]() . Знайдіть відношення площ описаного та вписаного в нього кругів.
. Знайдіть відношення площ описаного та вписаного в нього кругів.
542. Коло, вписане у прямокутний трикутник, ділить його гіпотенузу на два відрізки. Доведіть, що добуток довжин цих відрізків дорівнює площі трикутника.
543. У рівносторонній трикутник вписано коло. До цього кола і до сторін трикутника дотикаються три менші кола. Знайдіть сторону даного трикутника, якщо радіус малого кола дорівнює ![]() .
.
544. У коло, радіус якого дорівнює ![]() , вписано трикутник. Вершини трикутника ділять коло на три частини у відношенні
, вписано трикутник. Вершини трикутника ділять коло на три частини у відношенні ![]() . Знайдіть площу трикутника.
. Знайдіть площу трикутника.
545. У рівнобедрений трикутник вписано коло радіуса ![]() . До кола проведено дотичну, паралельну основі. В отриманий трикутник вписано коло радіуса
. До кола проведено дотичну, паралельну основі. В отриманий трикутник вписано коло радіуса ![]() . Доведіть, що косинус кута при основі цього трикутника дорівнює
. Доведіть, що косинус кута при основі цього трикутника дорівнює ![]() .
.
546. Висоти гострокутного трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Пряма, що містить висоту, проведену з вершини
. Пряма, що містить висоту, проведену з вершини ![]() , вдруге перетинає описане коло трикутника в точці
, вдруге перетинає описане коло трикутника в точці ![]() . Доведіть, що сторона
. Доведіть, що сторона ![]() перетинає відрізок
перетинає відрізок ![]() в його середині.
в його середині.
547. Радіус кола, вписаного в прямокутний трикутник, дорівнює піврізниці катетів. Знайдіть гострі кути трикутника.
548. У прямокутному трикутнику ![]()
![]() відрізок
відрізок ![]() – висота. Радіуси кіл, вписаних у трикутники
– висота. Радіуси кіл, вписаних у трикутники ![]() і
і ![]() , відповідно дорівнюють
, відповідно дорівнюють ![]() і
і ![]() . Знайдіть радіус кола, вписаного в трикутник
. Знайдіть радіус кола, вписаного в трикутник ![]() .
.
549. У трикутнику ![]() центри описаного та вписаного кіл симетричні відносно прямої
центри описаного та вписаного кіл симетричні відносно прямої ![]() . Знайдіть кути трикутника
. Знайдіть кути трикутника ![]() .
.
550. Прямі, що містять бісектриси кутів ![]() ,
, ![]() ,
, ![]() трикутника
трикутника ![]() , перетинають описане навколо цього трикутника коло в точках
, перетинають описане навколо цього трикутника коло в точках ![]() ,
, ![]() ,
, ![]() відповідно. Доведіть, що відрізки
відповідно. Доведіть, що відрізки ![]() і
і ![]() перпендикулярні.
перпендикулярні.
551. У гострокутному трикутнику ![]() проведено висоти
проведено висоти ![]() і
і ![]() . Точка
. Точка ![]() – центр кола, описаного навколо трикутника
– центр кола, описаного навколо трикутника ![]() . Доведіть, що відрізки
. Доведіть, що відрізки ![]() і
і ![]() перпендикулярні.
перпендикулярні.
552. Бісектриси кутів трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Навколо даного трикутника описано коло. Бісектриса кута
. Навколо даного трикутника описано коло. Бісектриса кута ![]() перетинає це коло в точці
перетинає це коло в точці ![]() . Доведіть, що
. Доведіть, що ![]() .
.
553. Точка ![]() належить стороні
належить стороні ![]() трикутника
трикутника ![]() . Доведіть, що відношення радіусів кіл, описаних навколо трикутників
. Доведіть, що відношення радіусів кіл, описаних навколо трикутників ![]() і
і ![]() , не залежить від вибору точки
, не залежить від вибору точки ![]() на стороні
на стороні ![]() .
.
554. На стороні ![]() трикутника
трикутника ![]() взято точку
взято точку ![]() . Кола, які вписано у трикутники
. Кола, які вписано у трикутники ![]() і
і ![]() , дотикаються. Доведіть, що
, дотикаються. Доведіть, що ![]() .
.
555. Довжини сторін трикутника утворюють арифметичну прогресію. Доведіть, що радіус кола, вписаного в даний трикутник, дорівнює ![]() висоти, проведеної до середньої за величиною сторони трикутника.
висоти, проведеної до середньої за величиною сторони трикутника.
556. У трикутник ![]() вписано коло. Дотична до кола перетинає сторони
вписано коло. Дотична до кола перетинає сторони ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Периметр трикутника
відповідно. Периметр трикутника ![]() дорівнює
дорівнює ![]() . Знайдіть довжину сторони
. Знайдіть довжину сторони ![]() , якщо периметр трикутника
, якщо периметр трикутника ![]() дорівнює
дорівнює ![]() .
.
557. Навколо трикутника ![]() описано коло. З довільної точки
описано коло. З довільної точки ![]() кола проведено перпендикуляри
кола проведено перпендикуляри ![]() і
і ![]() до прямих
до прямих ![]() і
і ![]() відповідно. Знайдіть положення точки
відповідно. Знайдіть положення точки ![]() , для якого довжина відрізка
, для якого довжина відрізка ![]() є найбільшою.
є найбільшою.
558. Сума радіусів вписаного та описаного кіл прямокутного трикутника дорівнює одному з катетів. Знайдіть гострі кути трикутника.
559. У трикутнику ![]() центри описаного та одного із зовніописаних кіл симетричні відносно прямої
центри описаного та одного із зовніописаних кіл симетричні відносно прямої ![]() . Знайдіть кути трикутника
. Знайдіть кути трикутника ![]() .
.
560. Продовження висот гострокутного трикутника ![]() , проведених до сторін
, проведених до сторін ![]() ,
, ![]() і
і ![]() , перетинають описане навколо цього трикутника коло в точках
, перетинають описане навколо цього трикутника коло в точках ![]() ,
, ![]() ,
, ![]() відповідно. Доведіть, що точка перетину бісектрис трикутника
відповідно. Доведіть, що точка перетину бісектрис трикутника ![]() збігається з ортоцентром трикутника
збігається з ортоцентром трикутника ![]() .
.
561. Через вершини ![]() і
і ![]() трикутника
трикутника ![]() проведено коло, яке перетинає сторони
проведено коло, яке перетинає сторони ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Пряма
відповідно. Пряма ![]() – дотична до кола, описаного навколо трикутника
– дотична до кола, описаного навколо трикутника ![]() . Доведіть, що прямі
. Доведіть, що прямі ![]() і
і ![]() паралельні.
паралельні.
562. У прямокутний трикутник вписано коло. Точка дотику ділить один із катетів у відношенні ![]() , рахуючи від вершини прямого кута. Відстань від центра вписаного кола до вершини прямого кута дорівнює
, рахуючи від вершини прямого кута. Відстань від центра вписаного кола до вершини прямого кута дорівнює ![]() см. Знайдіть сторони трикутника.
см. Знайдіть сторони трикутника.
563. Бісектриси кутів трикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Точка
. Точка ![]() – центр зовнівписаного кола, яке дотикається до сторони
– центр зовнівписаного кола, яке дотикається до сторони ![]() . Бісектриса кута
. Бісектриса кута ![]() перетинає описане навколо трикутника коло в точці
перетинає описане навколо трикутника коло в точці ![]() . Доведіть, що
. Доведіть, що ![]() .
.
564. Доведіть, що коло, яке проходить через ортоцентр трикутника і дві його вершини, дорівнює колу, описаному навколо трикутника.
565. Дотична в точці ![]() до кола, яке описане навколо трикутника
до кола, яке описане навколо трикутника ![]() , перетинає пряму
, перетинає пряму ![]() у точці
у точці ![]() , відрізок
, відрізок ![]() – бісектриса трикутника
– бісектриса трикутника ![]() . Доведіть, що
. Доведіть, що ![]() .
.
566. На стороні ![]() трикутника
трикутника ![]() взято точку
взято точку ![]() так, що
так, що ![]() . Доведіть, що кола, вписані в трикутники
. Доведіть, що кола, вписані в трикутники ![]() і
і ![]() , дотикаються.
, дотикаються.
567. Радіус кола, вписаного в трикутник, дорівнює ![]() однієї з його висот. Доведіть, що довжини сторін трикутника утворюють арифметичну прогресію.
однієї з його висот. Доведіть, що довжини сторін трикутника утворюють арифметичну прогресію.
568. У трикутник ![]() , периметр якого дорівнює
, периметр якого дорівнює ![]() , вписано коло. Дотична до кола перетинає сторони
, вписано коло. Дотична до кола перетинає сторони ![]() і
і ![]() у точках
у точках ![]() і
і ![]() відповідно. Знайдіть периметр трикутника
відповідно. Знайдіть периметр трикутника ![]() , якщо
, якщо ![]() .
.
Вписаний та описаний чотирикутник
569. Діагоналі описаного чотирикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Радіуси описаних кіл трикутників
. Радіуси описаних кіл трикутників ![]() ,
, ![]() ,
, ![]() ,
, ![]() відповідно дорівнюють
відповідно дорівнюють ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Доведіть, що
. Доведіть, що ![]() .
.
570. Діагоналі опуклого чотирикутника ![]() перетинаються в точці
перетинаються в точці ![]() . Радіуси описаних кіл трикутників
. Радіуси описаних кіл трикутників ![]() ,
, ![]() ,
, ![]() ,
, ![]() відповідно дорівнюють
відповідно дорівнюють ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Відомо, що
. Відомо, що ![]() . Доведіть, що в чотирикутник
. Доведіть, що в чотирикутник ![]() можна вписати коло.
можна вписати коло.
571. Знайдіть діагональ ![]() чотирикутника
чотирикутника ![]() , якщо навколо нього можна описати коло і
, якщо навколо нього можна описати коло і ![]() см,
см, ![]() см,
см, ![]() см,
см, ![]() см.
см.
572. Навколо рівнобічної трапеції з гострим кутом ![]() описано коло, і в цю трапецію вписано коло. Знайдіть відношення радіуса вписаного кола до радіуса описаного кола.
описано коло, і в цю трапецію вписано коло. Знайдіть відношення радіуса вписаного кола до радіуса описаного кола.
573. Центр кола, вписаного у прямокутну трапецію, віддалений від кінців її бічної сторони на ![]() см і
см і ![]() см. Знайдіть периметр трапеції.
см. Знайдіть периметр трапеції.
574. Основи трапеції дорівнюють ![]() см і
см і ![]() см. Знайдіть радіуси двох кіл: вписаного в трапецію й описаного навколо неї, коли відомо, що такі кола існують.
см. Знайдіть радіуси двох кіл: вписаного в трапецію й описаного навколо неї, коли відомо, що такі кола існують.
575. У рівнобічну трапецію вписано коло. Відстань від центра кола до точки перетину діагоналей трапеції відноситься як ![]() . Знайдіть відношення периметра трапеції до довжини кола.
. Знайдіть відношення периметра трапеції до довжини кола.
576. У рівнобічну трапецію вписано коло, радіус якого дорівнює ![]() см. Відстань між точками дотику, що лежать на її бічних сторонах, дорівнює
см. Відстань між точками дотику, що лежать на її бічних сторонах, дорівнює ![]() см. Знайдіть площу трапеції.
см. Знайдіть площу трапеції.
577. Периметр рівнобічної трапеції вдвічі більший за довжину вписаного в цю трапецію кола. Знайдіть гострий кут трапеції.
578. Висота рівнобічної трапеції вдвічі менша від бічної сторони. У цю трапецію вписано круг. Знайдіть відношення площі трапеції до площі вписаного круга.
579. У прямокутну трапецію вписано коло. Доведіть, що площа цієї трапеції дорівнює добутку її основ.
580. В опуклий чотирикутник ![]() можна вписати коло. Доведіть, що кола, вписані в трикутники
можна вписати коло. Доведіть, що кола, вписані в трикутники ![]() і
і ![]() , дотикаються одне до одного.
, дотикаються одне до одного.
581. У прямокутну трапецію ![]() (
(![]() ,
, ![]() ) вписано коло з центром
) вписано коло з центром ![]() . Знайдіть площу трапеції, якщо
. Знайдіть площу трапеції, якщо ![]() см,
см, ![]() см.
см.
582. Трапеція ![]()
![]() вписана в коло. Точка
вписана в коло. Точка ![]() – центр цього кола. Знайдіть площу трапеції, якщо
– центр цього кола. Знайдіть площу трапеції, якщо ![]() і
і ![]() .
.
583. Опуклий чотирикутник ![]() такий, що кола, вписані в трикутники
такий, що кола, вписані в трикутники ![]() і
і ![]() , дотикаються одне до одного. Доведіть, що в чотирикутник
, дотикаються одне до одного. Доведіть, що в чотирикутник ![]() можна вписати коло.
можна вписати коло.
584. У прямокутну трапецію ![]() (
(![]() ,
, ![]() ) вписано коло з центром
) вписано коло з центром ![]() . Знайдіть площу трапеції, якщо
. Знайдіть площу трапеції, якщо ![]() см,
см, ![]() см.
см.
585. Трапеція ![]()
![]() вписана в коло. Точка
вписана в коло. Точка ![]() – центр цього кола. Знайдіть площу трапеції, якщо
– центр цього кола. Знайдіть площу трапеції, якщо ![]() , а висота трапеції дорівнює
, а висота трапеції дорівнює ![]() .
.
586. Доведіть, що радіус ![]() кола, вписаного в прямокутну трапецію, обчислюється за формулою
кола, вписаного в прямокутну трапецію, обчислюється за формулою ![]() , де
, де ![]() і
і ![]() – довжини основ трапеції.
– довжини основ трапеції.
Координати
587. Запишіть рівняння кола з центром у точці ![]() , яке дотикається до прямої
, яке дотикається до прямої ![]() .
.
588. Запишіть рівняння кола з центром у точці ![]() , яке дотикається до прямої
, яке дотикається до прямої ![]() .
.
589. Дано коло ![]() . Знайдіть рівняння кола з центром
. Знайдіть рівняння кола з центром ![]() , яке дотикається до даного кола.
, яке дотикається до даного кола.
590. Дано коло ![]() . Знайдіть рівняння кола з центром
. Знайдіть рівняння кола з центром ![]() , яке дотикається до даного кола.
, яке дотикається до даного кола.
591. Дано точки ![]() і
і ![]() . Складіть рівняння прямої, яка перпендикулярна до прямої
. Складіть рівняння прямої, яка перпендикулярна до прямої ![]() і перетинає відрізок
і перетинає відрізок ![]() у точці
у точці ![]() такій, що
такій, що ![]() .
.
592. Дано точки ![]() і
і ![]() . Знайдіть рівняння прямої, яка перпендикулярна до прямої
. Знайдіть рівняння прямої, яка перпендикулярна до прямої ![]() і перетинає відрізок
і перетинає відрізок ![]() у точці
у точці ![]() такій, що
такій, що ![]() .
.
593. Знайдіть рівняння кола, описаного навколо трикутника ![]() з вершинами в точках
з вершинами в точках ![]() ,
, ![]() ,
, ![]() .
.
Вектори
594. Відомо, що ![]() ,
, ![]() ,
, ![]() . Знайдіть
. Знайдіть ![]() .
.
595. Відомо, що ![]() ,
, ![]() ,
, ![]() . Знайдіть
. Знайдіть ![]() .
.
596. Дано вектори ![]() і
і ![]() ,
, ![]() ,
, ![]() , кут між векторами
, кут між векторами ![]() і
і ![]() дорівнює
дорівнює ![]() . Знайдіть
. Знайдіть ![]() .
.
597. Нехай точки ![]() і
і ![]() – середини відрізків
– середини відрізків ![]() і
і ![]() відповідно. Доведіть, що
відповідно. Доведіть, що ![]() .
.
598. Нехай точки ![]() і
і ![]() – відповідно середини діагоналей
– відповідно середини діагоналей ![]() і
і ![]() чотирикутника
чотирикутника ![]() . Доведіть, що
. Доведіть, що ![]() .
.
599. Знайдіть кут між векторами ![]() і
і ![]() , якщо вектори
, якщо вектори ![]() і
і ![]() – перпендикулярні між собою і рівні за модулем.
– перпендикулярні між собою і рівні за модулем.
600. Знайдіть кут між векторами ![]() і
і ![]() , якщо вектори
, якщо вектори ![]() і
і ![]() – перпендикулярні між собою і рівні за модулем.
– перпендикулярні між собою і рівні за модулем.
1
![]()
Перетворення алгебраїчних виразів
1. ![]() .
.
4. ![]() .
.
5. ![]() .
.
6. ![]() і
і ![]() .
.
7. ![]() .
.
12. ![]() .
.
13. ![]() .
.
14. ![]() .
.
15. ![]() .
.
16. ![]() .
.
18. ![]()
![]()
![]()
19. ![]() .
.
22. ![]() .
.
23. ![]() .
.
25. ![]() або
або ![]() .
.
26. ![]() або
або ![]() .
.
27. ![]() .
.
28. ![]() і
і ![]() .
.
Властивості функції
38. ![]() .
.
39. ![]() .
.
40. ![]() .
.
41. ![]() .
.
Побудова графіків функцій, рівнянь та нерівностей
42. Рис. до завдання.
43. Рис. до завдання.
45. Рис. до завдання.

47. Рис. до завдання.
48. Рис. до завдання.
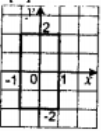
49. Рис. до завдання.

52. Рис. до завдання.

53. Графік – точки виду ![]() .
.
54. Графік – точки виду ![]() .
.
55. Рис. до завдання.

56. Рис. до завдання.
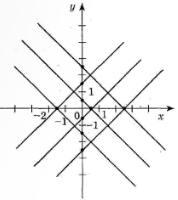
57. Рис. до завдання.
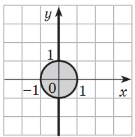
58. Рис. до завдання.

Побудова на координатній площині рівнянь, нерівностей та їх систем
59. Рис. до завдання.
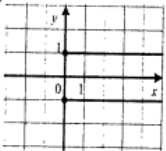
61. Рис. до завдання.
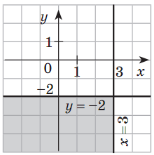
63. Рис. до завдання.
64. Рис. до завдання.
65. Рис. до завдання.
66. Рис. до завдання.
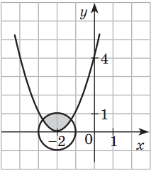
67. Рис. до завдання.
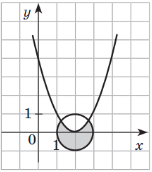
Елементи комбінаторики та теорії ймовірностей
68. ![]() .
.
69. ![]() .
.
70. ![]() .
.
71. ![]() .
.
72. ![]() .
.
73. ![]() .
.
74. ![]() .
.
75. ![]() .
.
76. ![]() .
.
77. ![]() .
.
78. ![]() .
.
79. ![]() .
.
80. ![]() .
.
81. ![]() .
.
82. ![]() .
.
83. ![]() .
.
Рівняння
84. ![]() .
.
85. ![]() ;
; ![]() .
.
86. ![]() ;
; ![]() .
.
87. ![]() .
.
88. ![]() .
.
89. ![]() .
.
90. ![]() ;
; ![]() .
.
91. ![]() .
.
92. ![]() .
.
93. ![]() ;
; ![]() .
.
94. ![]() ;
; ![]() .
.
95. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
96. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
97. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
98. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
99. ![]() ;
; ![]() ;
; ![]() .
.
100. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
101. ![]() ;
; ![]() .
.
102. ![]() ;
; ![]() .
.
103. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
104. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
105. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
106. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
107. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
108. ![]() ;
; ![]() .
.
109. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
110. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
111. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Теорема Вієта
112. ![]() .
.
113. ![]() .
.
114. ![]() .
.
116. ![]() .
.
117. ![]() .
.
Рівняння з параметрами
118. При ![]() або
або ![]() .
.
119. При ![]() .
.
120. При ![]() .
.
121. При ![]() .
.
122. При ![]() .
.
123. При ![]() .
.
124. При ![]() .
.
125. При ![]() .
.
126. При ![]() .
.
127. При ![]() або
або ![]() .
.
128. При ![]() .
.
130. При ![]() .
.
131. При ![]() або
або ![]() .
.
132. При ![]() .
.
133. При ![]() .
.
134. Якщо ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки.
, то три розв’язки.
135. Якщо ![]() і
і ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() і
і ![]() , то три розв’язки.
, то три розв’язки.
136. При ![]() або
або ![]() .
.
137. При ![]() або
або ![]() .
.
138. При ![]() або
або ![]() .
.
139. При ![]() або
або ![]() .
.
140. При ![]() або
або ![]() .
.
141. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
142. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
143. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то 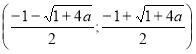 ; якщо
; якщо ![]() , то
, то 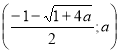 .
.
144. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то чотири розв’язки.
, то чотири розв’язки.
145. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то чотири розв’язки.
, то чотири розв’язки.
146. При ![]() або
або ![]() .
.
147. При ![]() або
або ![]() .
.
148. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то шість розв’язків; якщо
, то шість розв’язків; якщо ![]() , то чотири розв’язки; якщо
, то чотири розв’язки; якщо ![]() , то два розв’язки.
, то два розв’язки.
149. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то шість розв’язків; якщо
, то шість розв’язків; якщо ![]() , то чотири розв’язки; якщо
, то чотири розв’язки; якщо ![]() , то два розв’язки.
, то два розв’язки.
150. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то чотири розв’язки.
, то чотири розв’язки.
151. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то чотири розв’язки.
, то чотири розв’язки.
152. Якщо ![]() , то безліч розв’язків; якщо
, то безліч розв’язків; якщо ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то розв’язків немає.
, то розв’язків немає.
153. Якщо ![]() або
або ![]() , то безліч розв’язків; якщо
, то безліч розв’язків; якщо ![]() , то один розв’язок; якщо
, то один розв’язок; якщо ![]() або
або ![]() , то розв’язків немає.
, то розв’язків немає.
154. При ![]() .
.
155. При ![]() .
.
156. При ![]() .
.
157. При ![]() або
або ![]() .
.
158. Якщо ![]() , або
, або ![]() , або
, або ![]() , або
, або ![]() , то
, то ![]() або
або ![]() ; якщо
; якщо ![]() або
або ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає
, то розв’язків немає
159. При ![]() .
.
160. При ![]() .
.
161. При ![]() або
або ![]() .
.
162. ![]() .
.
163. При ![]() , або
, або ![]() , або
, або ![]() .
.
164. При ![]() , або
, або ![]() , або
, або ![]() .
.
165. При ![]() , або
, або ![]() , або
, або ![]() .
.
166. При ![]() або
або ![]() .
.
167. При ![]() або
або ![]() .
.
168. При ![]() .
.
169. При ![]() .
.
170. При ![]() ,
, ![]() .
.
171. При ![]() ,
, ![]() .
.
172. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то два розв’язки; якщо
, то два розв’язки; якщо ![]() , то три розв’язки; якщо
, то три розв’язки; якщо ![]() , то чотири розв’язки.
, то чотири розв’язки.
173. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то один розв’язок; якщо
, то один розв’язок; якщо ![]() , то два розв’язки.
, то два розв’язки.
174. При ![]() .
.
175. Якщо ![]() , то
, то ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає.
, то розв’язків немає.
176. Якщо ![]() або
або ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
177. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() ,
, ![]() ;
; ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() ,
, ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() .
.
178. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ,
, ![]() .
.
179. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
180. Якщо ![]() або
або ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
181. При ![]() .
.
182. При ![]() .
.
183. При ![]() .
.
184. При ![]() .
.
Нерівності
185. ![]() .
.
186. ![]() .
.
187. ![]() .
.
188. ![]() .
.
189. ![]() .
.
190. ![]() .
.
191. ![]() .
.
192. ![]() .
.
193. ![]() .
.
194. ![]() .
.
195. ![]() .
.
196. ![]() .
.
197. ![]() .
.
198. ![]() .
.
199. ![]() .
.
200. ![]() .
.
201. ![]() .
.
202. ![]() .
.
203. ![]() .
.
204. ![]() .
.
205. ![]() .
.
206. ![]() .
.
207. ![]() .
.
208. ![]() .
.
209. ![]() .
.
210. ![]() .
.
211. ![]() .
.
212. ![]() .
.
213. ![]() .
.
214. ![]() .
.
215. ![]() .
.
216. ![]() .
.
217. ![]() .
.
218. ![]() .
.
219. ![]() .
.
220. ![]() .
.
Нерівності з параметрами
243. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() або
або ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
244. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() або
або ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
245. Якщо ![]() , то
, то ![]() або
або ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
246. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() .
.
247. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
248. Якщо ![]() , то
, то ![]() або
або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() , або
, або ![]() , або
, або ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
249. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() .
.
250. При ![]() .
.
251. При ![]() .
.
252. При ![]() .
.
253. При ![]() .
.
254. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
255. Якщо ![]() , то
, то ![]() ; якщо
; якщо ![]() , то розв’язків немає.
, то розв’язків немає.
256. Якщо ![]() , то безліч розв’язків; якщо
, то безліч розв’язків; якщо ![]() , то
, то ![]() або
або ![]() ; якщо
; якщо ![]() , то
, то ![]() або
або ![]() .
.
Системи рівнянь
257. ![]() ;
; ![]() .
.
258. ![]() ;
; ![]() .
.
259. ![]() ;
; ![]() .
.
260. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
261. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
262. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
263. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
264. ![]() .
.
265. ![]() ;
; ![]() .
.
266. ![]() ;
; ![]() .
.
267. ![]() ;
; ![]() .
.
268. ![]() ;
; ![]() ;
; ![]() .
.
269. ![]() ;
; ![]() .
.
270. ![]() ;
; ![]() .
.
271. ![]() .
.
272. ![]() .
.
273. ![]() ;
; ![]() ;
; 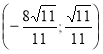 ;
; 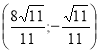 .
.
274. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
275. ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
276. ![]() ;
; ![]() ;
;  ;
; 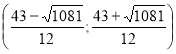 .
.
277. ![]() ;
; ![]() ;
; 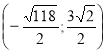 ;
; 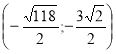 .
.
278. ![]() ;
; ![]() ;
; 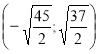 ;
; 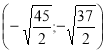 .
.
279. ![]() .
.
280. ![]() ;
; ![]() .
.
281. ![]() .
.
282. ![]() .
.
283. ![]() .
.
284. ![]() .
.
Системи рівнянь та нерівностей з параметрами
285. При ![]() .
.
286. При ![]() .
.
287. При ![]() .
.
288. При ![]() .
.
289. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то один розв’язок; якщо
, то один розв’язок; якщо ![]() , то два розв’язки.
, то два розв’язки.
290. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то один розв’язок; якщо
, то один розв’язок; якщо ![]() , то два розв’язки.
, то два розв’язки.
291. При ![]() .
.
292. При ![]() .
.
293. При ![]() .
.
294. При ![]() або
або ![]() .
.
295. При ![]() або
або ![]() .
.
296. При ![]() або
або ![]() .
.
297. При ![]() або
або ![]() .
.
298. При ![]() .
.
299. При ![]() .
.
300. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то один розв’язок.
, то один розв’язок.
301. Якщо ![]() , то розв’язків немає; якщо
, то розв’язків немає; якщо ![]() , то один розв’язок.
, то один розв’язок.
302. При ![]() .
.
303. При ![]() .
.
304. Таких значень параметра ![]() не існує.
не існує.
305. При ![]() або
або ![]() .
.
306. При ![]() .
.
307. При ![]() .
.
308. При ![]() .
.
309. При ![]() .
.
310. При ![]() або
або ![]() .
.
311. При ![]() .
.
312. При ![]() .
.
313. При ![]() .
.
314. При ![]() .
.
![]()
Кути та відрізки на площині
315. Рис. до завдання.
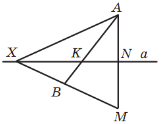
318. ![]() см.
см.
320. ![]() см.
см.
Трикутник та його елементи
322. ![]() .
.
323. ![]() .
.
324. ![]() ,
, ![]() .
.
325. ![]() .
.
326. ![]() .
.
327. ![]() .
.
328. ![]() .
.
329. ![]() .
.
330. ![]() .
.
331. ![]() см.
см.
332. ![]() см,
см, ![]() см,
см, ![]() см.
см.
333. ![]() .
.
334. ![]() см.
см.
335. ![]() ,
, ![]() ,
, ![]() .
.
336. ![]() см.
см.
337. ![]() ,
, ![]() ,
, ![]() .
.
338. ![]() см.
см.
339. ![]() ,
, ![]() .
.
340. ![]() .
.
341. ![]() .
.
342. ![]() .
.
343. ![]() .
.
344. ![]() .
.
345. ![]() .
.
346. ![]() см,
см, ![]() см.
см.
347. ![]() см.
см.
348. ![]() см.
см.
349. ![]() см.
см.
350. ![]() ,
, ![]() ,
, ![]() .
.
Геометричні побудови у трикутнику
389. Рис. до завдання.
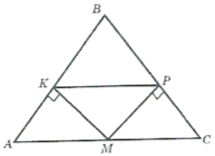
390. Рис. до завдання.
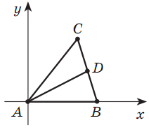
Площа трикутника
396. ![]() .
.
397. ![]() .
.
398. ![]() .
.
399. ![]() .
.
400. ![]() .
.
401. ![]() .
.
402. ![]() .
.
403. ![]() см2.
см2.
404. ![]() см2.
см2.
405. ![]() см2.
см2.
407. ![]() .
.
408. ![]() .
.
409. ![]() .
.
410. ![]() .
.
Чотирикутник
420. ![]() см2.
см2.
421. ![]() см2.
см2.
422. ![]() ,
, ![]() .
.
424. ![]() ,
, ![]() .
.
425. ![]() дм2.
дм2.
426. ![]() .
.
427. ![]() .
.
428. ![]() .
.
429. ![]() .
.
Паралелограм
432. ![]() .
.
433. ![]() .
.
439. ![]() см і
см і ![]() см або
см або ![]() см і
см і ![]() см.
см.
443. ![]() .
.
Прямокутник і квадрат
444. ![]() .
.
445. ![]() ,
, ![]() .
.
447. ![]() .
.
449. ![]() см або
см або ![]() см.
см.
450. ![]() .
.
Трапеція
455. ![]() .
.
456. ![]() .
.
459. ![]() см.
см.
460. ![]() .
.
461. ![]() см.
см.
464. ![]() см,
см, ![]() см.
см.
471. ![]() см.
см.
472. ![]() см,
см, ![]() см.
см.
473. ![]() .
.
474. ![]() см,
см, ![]() см.
см.
475. ![]() ,
, ![]() .
.
477. ![]() .
.
478. ![]() см2.
см2.
479. ![]() см2.
см2.
482. ![]() см2.
см2.
Коло та його елементи
487. ![]() см.
см.
488. ![]() .
.
489. ![]() см.
см.
495. ![]() .
.
496. 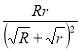 .
.
497. ![]() дм2.
дм2.
499. ![]() .
.
506. ![]() .
.
507. ![]() .
.
509. ![]() .
.
Вписаний та описаний трикутник
512. ![]() .
.
513. ![]() .
.
517. ![]() см.
см.
520. ![]() см.
см.
521. ![]() .
.
522. ![]() см,
см, ![]() см,
см, ![]() см.
см.
523. ![]() см.
см.
524. ![]() см.
см.
525. ![]() .
.
530. ![]() .
.
534. ![]() .
.
535. ![]() см.
см.
536. ![]() см.
см.
537. ![]() ,
, ![]() .
.
538. ![]() см.
см.
539. ![]() ,
, ![]() .
.
540. ![]() .
.
541. ![]() .
.
543. ![]() .
.
544. ![]() .
.
547. ![]() ,
, ![]() .
.
548. ![]() .
.
549. ![]() ,
, ![]() ,
, ![]() .
.
556. ![]() .
.
557. Хорда ![]() повинна бути максимальною, бути діаметром описаного навколо
повинна бути максимальною, бути діаметром описаного навколо ![]() кола.
кола.
558. ![]() ,
, ![]() .
.
559. ![]() ,
, ![]() ,
, ![]() .
.
562. ![]() см,
см, ![]() см,
см, ![]() см.
см.
568. ![]() .
.
Вписаний та описаний чотирикутник
571. ![]() см.
см.
572. 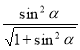 .
.
573. ![]() см.
см.
574. ![]() см,
см, ![]() см.
см.
575. ![]() .
.
576. ![]() см2.
см2.
577. ![]() .
.
578. ![]() .
.
581. ![]() см2.
см2.
582. ![]() .
.
584. ![]() см2.
см2.
585. ![]() .
.
Координати
587. ![]() .
.
588. ![]() .
.
589. ![]() .
.
590. ![]() .
.
591. ![]() .
.
592. ![]() .
.
593. ![]() .
.
Вектори
594. ![]() .
.
595. ![]() .
.
596. ![]() .
.
599. ![]() .
.
600. ![]() .
.
Список використаної літератури
1. Збірник завдань для державної підсумкової атестації з математики. 9 клас. / М. І. Бурда, О. П. Вашуленко, Н. С. Прокопенко. – Х.: Гімназія, 2010. – 256 с.
2. Збірник завдань для державної підсумкової атестації з математики: 9 кл. / О. С. Істер, О. І. Глобін, О. В. Комаренко. – К.: Центр навч.-метод. л-ри, 2011. – 112 с.: іл.
3. Збірник завдань для державної підсумкової атестації з математики: 9 кл. / О. С. Істер, О. І. Глобін, О. В. Комаренко. – 2-ге вид., доопрац. – К.: Центр навч.-метод. л-ри, 2012. – 112 с.: іл.
4. Збірник завдань для державної підсумкової атестації з математики: 9-й кл. / О. І. Глобін та ін. – К.: Центр навч.-метод. л-ри, 2013. – 168 с.: іл.
5. Збірник завдань для державної підсумкової атестації з математики: 9-й кл. / А. Г. Мерзляк [та ін.]; за ред. М. І. Бурди. – К.: Центр навч.-метод. л-ри, 2014. – 256 с.
6. Навчальна програма для загальноосвітніх навчальних закладів “Математика. 5 – 9 класи” (авт. М. І. Бурда, Ю. І. Мальований, Є. П. Нелін, Д. А. Номіровський, А. В. Паньков, Н. А. Тарасенкова, М. В. Чемерис, М. С. Якір).
1


про публікацію авторської розробки
Додати розробку
