Збірник завдань для ДПА з математики. 9 клас
НВК: ЗАГАЛЬНООСВІТНЯ ШКОЛА І – ІІ СТ. №34 –
ЕКОНОМІКО-ПРАВОВИЙ ЛІЦЕЙ «СУЧАСНИК» - ДЮЦ
Завдання
державної підсумкової
атестації
з математики
9 клас
м. Кропивницький - 2019
СТРУКТУРА, ЗМІСТ та ОЦІНЮВАННЯ завдань атестаційної роботи
У першій частині атестаційної роботи пропонується 12 завдань з вибором однієї правильної відповіді, з яких тільки одна є правильною. Завдання з вибором однієї відповіді вважається виконаним правильно, якщо в бланку відповідей указано тільки одну літеру, якою позначена правильна відповідь. При цьому будь-які міркування, що пояснюють вибір учня не перевіряються і не оцінюються.
Друга частина атестаційної роботи складається із 4 завдань відкритої форми з короткою відповіддю. Завдання цієї частини вважається виконаним правильно, якщо в бланку відповідей записана правильна відповідь (наприклад, число, вираз, корені рівняння). Усі необхідні обчислення, перетворення виконуються на чернетках.
Правильне розв’язання кожного із завдань 2.1 – 2.4 оцінюється двома балами: якщо у бланку відповідей указано правильну відповідь до завдання, то за це нараховується 2 бали, якщо ж указана учнем відповідь є неправильною, то бали за таке завдання не нараховуються.
Якщо учень вважає за потрібне внести зміни у відповідь до якогось із завдань першої чи другої частини, то він має це зробити у спеціально відведеній для цього частині бланка. Таке виправлення не веде до втрати балів. Якщо ж виправлення зроблено в основній частині бланка відповідей, то бали за таке завдання не нараховуються. Якщо відповідь виправлена на неправильну (тобто в основній частині було вказано правильну відповідь, а потім зроблено виправлення), то бали за таке завдання не нараховуються.
Третя частина складається із трьох завдань відкритої форми з розгорнутою відповіддю. Такі завдання вважаються виконаними правильно, якщо учень навів розгорнутий запис розв’язування з обгрунтуванням кожного його етапу та дав правильну відповідь. Завдання третьої частини виконуються на аркушах зі штампом школи. Формулювання завдань третьої частини учень не переписує, а вказує тільки номер завдання.
Правильне розв’язання завдання 3.1 оцінюється 4 балами, завдань 3.2 та 3.3 – 6 балами.
Критерії оцінювання завдань третьої частини.
|
Що виконав учень |
Відповідна кількість балів |
|
|
3.2 та 3.3 (6 балів) |
3.1 (4 бали) |
|
|
Отримав правильну відповідь і навів повне обгрунтування |
6 |
4 |
|
Отримав правильну відповідь, але вона недостатньо обгрунтована або містить незначні недоліки |
5 |
3 |
|
Отримав відповідь, записав правильний хід розв’язування завдання, але в процесі розв’язування припустився помилки обчислювального або логічного (при обгрунтуванні) характера |
4 |
|
|
Суттєво наблизився до правильного кінцевого результату або в результаті знайшов лише частину правильної відповіді |
3 |
2 |
|
Розпочав розв’язувати завдання правильно, але в процесі розв’язування припустився помилки у застосуванні необхідного твердження чи формули |
2 |
1 |
|
Лише розпочав правильно розв’язувати завдання або розпочав неправильно, але наступні етапи розв’язування виконав правильно |
1 |
|
|
Розв’язання не відповідає жодному з наведених вище критеріїв |
0 |
0 |
Виправлення і закреслення в оформленні розв’язання завдань третьої частини, якщо вони зроблені акуратно, не є підставою для зниження оцінки.
Таблиця нарахування балів
|
Номери завдань |
Кількість балів |
Усього |
|
1.1 – 1.12 |
по 1 балу |
12 балів |
|
2.1 – 2.4 |
по 2 бали |
8 балів |
|
3.1 |
4 бали |
4 бали |
|
3.2, 3.3 |
по 6 балів |
12 балів |
|
Сума балів |
36 балів |
|
Таблиця переводу кількості балів в оцінку за 12-ти бальною шкалою
|
Кількість набраних балів |
Оцінка за 12-ти бальною шкалою |
|
0 – 2 |
1 |
|
3 – 4 |
2 |
|
5 – 6 |
3 |
|
7 – 8 |
4 |
|
9 – 10 |
5 |
|
11 – 12 |
6 |
|
13 – 16 |
7 |
|
17 – 20 |
8 |
|
21 – 24 |
9 |
|
25 – 28 |
10 |
|
29 – 32 |
11 |
|
33 – 36 |
12 |
Р О Б О Т А
на державну підсумкову атестацію
з математики
за курс основної школи
учня / учениці 9 ___ класу
навчально-виховного комплексу:
загальноосвітня школа І – ІІ ступенів №34 –
економіко-правовий ліцей «Сучасник» - ДЮЦ
Міської ради м. Кропивницький
Прізвище, ім’я, по батькові учня (учениці)
Варіант №______
|
Кількість балів |
Перша частина |
Друга частина |
Третя частина |
Всього |
|
|
|
|
|
|
|
Оцінка за 12 – ти бальною шкалою |
|
|||
Голова атестаційної комісії _______________
Вчитель _______________
Член комісії _______________
УВАГА! Відмічайте лише один варіант відповіді у рядку варіантів відповідей до кожного завдання. Будь-які виправлення у бланку недопустимі.
Якщо Ви вирішили змінити відповідь у деяких завданнях, то правильну відповідь можна зазначити в спеціально відведеному місці, розташованому внизу бланку відповідей.
![]() У завданнях 1.1 – 1.12 правильну відповідь позначайте тільки так:
У завданнях 1.1 – 1.12 правильну відповідь позначайте тільки так:
У завданнях 2.1 – 2.4 запишіть відповідь:
2.1 ______________________________ 2.2___________________________
2.3______________________________ 2.4___________________________
Щоб виправити відповідь до завдання, запишіть його номер у спеціально відведеній клітинці, а правильну, на Вашу думку, відповідь – у відповідному місці.
Завдання 1.1 – 1.12 Завдання 2.1 – 2.4
А Б В Г
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
Перша частина |
|||||||||||
|
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
1.8 |
1.9 |
1.10 |
1.11 |
1.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.1 |
2.2 |
2.3 |
2.4 |
3.1 |
3.2 |
3.3 |
|
|
|
|
|
|
|
|
ВАРІАНТ 1
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Запишіть 3 год 24 хв у хвилинах.
А) 324 хв ; Б) 27 хв ; В) 54 хв ; Г) 204 хв .
1.2. Знайдіть різницю ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
1.3. Який з одночленів подано в стандартному вигляді?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Знайдіть нулі функції ![]()
А) 5 і 3 ; Б) -3 ; В) 5 ; Г) 3
1.5. Виконайте множення ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
 1.6. Внесіть множник під знак кореня
1.6. Внесіть множник під знак кореня ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
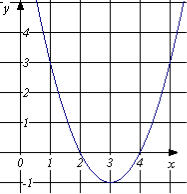
1.7. На рисунку зображено графік функції ![]() . Укажіть проміжок спадання функції.
. Укажіть проміжок спадання функції.
А) [ 2 ; 4] ; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
 1.8. Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?
1.8. Вкладник поклав до банку 1500 грн. Під який відсоток річних покладено гроші, якщо через рік на рахунку вкладника було 1725 грн.?
А) 85% ; Б) 115% ; В) 25% ; Г) 15% .
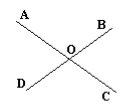
1.9. Який кут вертикальний з ![]() (див. рис.)?
(див. рис.)?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.10. Знайдіть меншу основу рівнобічної трапеції, якщо висота, проведена з вершини тупого кута, ділить більшу основу на відрізки 4 дм і 16 дм.
А) 8 дм ; Б) 16 дм ; В) 10 дм ; Г) 12 дм.
1.11. Сторони паралелограма дорівнюють 10 см і 15 см, а один з його кутів - 150°. Знайдіть площу паралелограма.
А) 37,5 см2 ; Б) 50 см2 ; В) ![]() см2 ; Г) 75 см2 .
см2 ; Г) 75 см2 .
1.12. Відстань від точки А (1 ; 2) до точки В (-2 ; y) дорівнює 5. Знайдіть значення y.
А) -2 ; Б) -6 ; 2 ; В) -2 ; 6 ; Г) 6 .
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння ![]()
2.2. Побудуйте графіки функцій ![]() і
і ![]() . У бланк відповідей запишіть значення
. У бланк відповідей запишіть значення ![]() , при яких значення функції
, при яких значення функції ![]() менше за значення функції
менше за значення функції ![]() .
.
2.3. Знайдіть знаменник геометричної прогресії ![]() , у якої
, у якої ![]() .
.
2.4. Один з катетів прямокутного трикутника дорівнює 12 см, а інший – на 8 см менший за гіпотенузу. Знайдіть периметр трикутника.
Частина третя
3.1. Різниця половини одного числа і третини другого числа дорівнює 2. Якщо ж перше число зменшити на його чверть, а друге число збільшити на шосту його частину, то сума отриманих чисел дорівнюватиме 53. Знайдіть ці числа.
3.2. Спростіть вираз: ![]()
3.3. Кути паралелограма відносяться як 2 : 3. Знайдіть кут між висотами паралелограма, проведеними з вершини гострого кута.
ВАРІАНТ 2
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Яке з рівнянь не має коренів?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.2. Виконайте ділення ![]()
А) 25 ; Б) ![]() ; В)
; В) ![]() ; Г) 4
; Г) 4
1.3. Запишіть двочлен ![]() у вигляді добутку.
у вигляді добутку.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Спростіть вираз ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Яка з рівностей є тотожністю?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Виконайте множення: ![]() .
.
 А)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() .
.
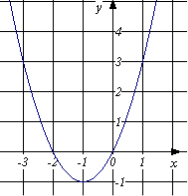
1.7. На рисунку зображено графік функції ![]() . Знайдіть множину розв’язків нерівності
. Знайдіть множину розв’язків нерівності ![]() .
.
А) ![]() ; Б) [-1 ; 0] ; В) [-2 ; 0] ; Г) (-2 ; 0)
; Б) [-1 ; 0] ; В) [-2 ; 0] ; Г) (-2 ; 0)
1.8. Знайдіть нулі функції: ![]()
А) 0 ; Б) 1 ; В) 0 ; 1 ; Г) -1.
1.9. На рисунку зображено паралельні прямі a і b, які перетинає січна d. Користуючись рисунком, знайдіть ![]() , якщо
, якщо ![]() .
.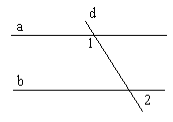 А) 150° ; Б) 30° ; В) 60° ; Г) 120°
А) 150° ; Б) 30° ; В) 60° ; Г) 120°
1.10. Знайдіть центральний кут, якщо відповідна йому дуга становить ![]() кола.
кола.
А) 90° ; Б) 30° ; В) 120° ; Г) 150°
1.11. Знайдіть внутрішній кут при вершині правильного шестикутника.
А) 90° ; Б) 100° ; В) 120° ; Г) 150° .
1.12. Знайдіть площу трикутника, периметр якого 24 см, а радіус кола, вписаного в цей трикутник, дорівнює 4 см.
А) 24 см2 ; Б) 32 см2 ; В) 48 см2 ; Г) 96 см2 .
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Скоротіть дріб: ![]()
2.2. Розкладіть на множники квадратний тричлен ![]() .
.
2.3. З натуральних чисел від 1 до 24 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 24?
2.4. У паралелограмі ABCD бісектриса кута А ділить сторону ВС на відрізки ВК = 3 см, КС = 2 см. Знайдіть периметр паралелограма.
Частина третя
3.1. Перша бригада може виконати завдання на 6 год швидше, ніж друга. Через 2 год після того, як почала працювати друга бригада, до неї приєдналася перша. Через 3 год спільної роботи виявилося, що виконано ![]() завдання. За скільки годин може виконати завдання кожна бригада, працюючи окремо?
завдання. За скільки годин може виконати завдання кожна бригада, працюючи окремо?
3.2. Знайдіть область визначення функції: ![]()
3.3. Діагональ рівнобічної трапеції ділить навпіл її тупий кут, а середню лінію трапеції на відрізки 4 см і 5 см. Знайдіть периметр трапеції.
ВАРІАНТ 3
Частина перша
 Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
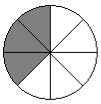
- Яку частину круга заштриховано?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.2. Скільки кілограмів сушених грибів отримають з 18 кг свіжих, якщо з 12 кг свіжих грибів отримали 1,8 кг сушених?
А) 5,4 кг ; Б) 3,6 кг ; В) 2,7 кг ; Г) 0,9 кг
1.3. Знайдіть значення аргументу, при якому функція ![]() має значення 3.
має значення 3.
А) 2 ; Б) ![]() ; В)
; В) ![]() ; Г) 7
; Г) 7
1.4. Спростіть вираз: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Обчисліть значення виразу: ![]()
А) ![]() ; Б) -6 ; В) 2 ; Г) 6
; Б) -6 ; В) 2 ; Г) 6
1.6. Спростіть вираз: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. Яку суму отримає на рахунок вкладник через рік, якщо він поклав до банку 5000 грн. під 15% річних?
А) 750 грн.; Б) 5075 грн.; В) 5750 грн.; Г) 5015 грн.
1.8. Розв’яжіть нерівність: ![]()
А) ![]() ; Б) [-3 ; 5] ; В)
; Б) [-3 ; 5] ; В) ![]() ; Г)
; Г) ![]()
1.9. Визначте вид трикутника MNK, якщо ![]()
А) визначити неможливо; Б) тупокутний ; В) гострокутний ; Г) прямокутний
1.10. Укажіть правильну рівність.
А) ![]() ; Б)
; Б) ![]() ; В)
; В)![]() ; Г)
; Г) ![]()
1.11. Точка M – середина відрізка АВ. Знайдіть координати точки М, якщо А(2 ; -3) , В(-6 ; 7).
А) (-2 ; 2) ; Б) (4 ; -5) ; В) (-4 ; 4) ; Г) (2 ; -2)
1.12. Коло вписано у правильний шестикутник зі стороною ![]() см. Знайдіть площу круга, обмеженого даним колом.
см. Знайдіть площу круга, обмеженого даним колом.
А) 36π см2 ; Б) 6π см2 ; В) 16π см2 ; Г) 48π см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Знайдіть цілі розв’язки нерівності: ![]()
2.3. Побудуйте графік функції ![]() . У бланк відповідей запишіть проміжок спадання функції.
. У бланк відповідей запишіть проміжок спадання функції.
2.4. У прямокутній трапеції гострий кут дорівнює 60°. Більша бічна сторона і більша основа дорівнюють по 12 см. Знайдіть середню лінію трапеції.
Частина третя
3.1. У кінотеатрі було 390 місць, розташованих однаковими рядами. Після того як місць у кожному ряду збільшили на 4 і додали ще один ряд, місць стало 480. Скільки стало рядів у кінотеатрі?
3.2. Складіть квадратне рівняння, корені якого у 2 рази більші за відповідні корені рівняння ![]()
3.3. Катети прямокутного трикутника дорівнюють 12 см і 16 см. Знайдіть довжину бісектриси трикутника, що проведена з вершини більшого гострого кута.
ВАРІАНТ 4
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- З поля площею 6.4 га зібрали 320 ц зерна. Який урожай зібрали в середньому з кожного гектара?
А) 20 ц ; Б) 24 ц; В) 50 ц; Г) 64 ц
1.2. Яка з числових нерівностей є правильною?
А) -37,5 > 3,5 ; Б) -5000 > -400 ; В) -475 < -375 ; Г) 0 < -20,7
1.3. Знайдіть розв’язок системи: ![]()
А) (2 ; -4) ; Б) (4 ; -2) ; В) (-2 ; 4) ; Г) (-4 ; 2)
1.4. Розв’яжіть рівняння: ![]()
А) 2 ; Б) -6 ; В) 0 ; Г) -2
1.5. Укажіть многочлен, який тотожно дорівнює виразу: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Виконайте віднімання: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. Знайдіть знаменник геометричної прогресії: 6 ; -2 ; ![]()
А) -3 ; Б) 3 ; В) ![]() ; Г)
; Г) ![]()
1.8. Оцініть значення виразу ![]() , якщо
, якщо ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
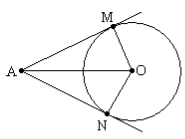 1.9. На рисунку AM і AN – дотичні до кола з центром у точці О. Відомо, що
1.9. На рисунку AM і AN – дотичні до кола з центром у точці О. Відомо, що ![]() Знайдіть
Знайдіть ![]() .
.
А) 50° ; Б) 30° ; В) 25° ; Г) 15°
1.10. Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють 3 см і ![]() см.
см.
А) 16 см ; Б) ![]() см ; В) 4 см ; Г) 5 см
см ; В) 4 см ; Г) 5 см
1.11. Знайдіть модуль вектора ![]()
А) 1 ; Б) 5 ; В) 7 ; Г) 25
1.12. У гострокутному трикутнику![]() . Знайдіть
. Знайдіть ![]() трикутника
трикутника ![]() .
.
А) 30° ; Б) 60° ; В) 75° ; Г) 45°
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть значення виразу: 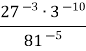
2.2. Спростіть вираз: ![]() , якщо
, якщо ![]()
2.3. Знайдіть область визначення функції: ![]()
2.4. Сторони трикутника відносяться як 6 : 7 : 8. Знайдіть периметр подібного йому трикутника, середня за довжиною сторона якого дорівнює 21 см.
Частина третя
3.1. Знайдіть три послідовних натуральних числа, якщо потроєний квадрат меншого з них на 67 більший, ніж сума квадратів другого і третього.
3.2. Розв’яжіть систему рівнянь: ![]()
3.3. Діагональ рівнобічної трапеції перпендикулярна до її бічної сторони. Знайдіть площу трапеції, якщо її основи дорівнюють 12 см і 20 см.
ВАРІАНТ 5
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
1.1. Яка числова нерівність є правильною?
А) 2591 > 2501 ; Б) 3031 < 3021 ; В) 780325 > 783025 ; Г) 44371 > 44381
1.2. Укажіть число, яке ділиться на 5 і на 3.
А) 2835 ; Б) 2358 ; В) 2585 ; Г) 8253
1.3. Скільки коренів має рівняння: ![]() ?
?
А) два ; Б) один ; В) безліч ; Г) жодного
1.4. Розв’язком якого рівняння є пара чисел (1 ; -1) ?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Виконайте віднімання: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Чому дорівнює добуток коренів квадратного рівняння ![]() ?
?
А) -7 ; Б) -6 ; В) 6 ; Г) 7
1.7. На якому рисунку графічно зображено множину розв’язків нерівності ![]() ?
?
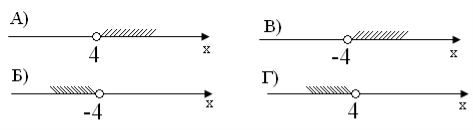
1.8. Знайдіть четвертий член геометричної прогресії: ![]() ; -1 ; 3 …
; -1 ; 3 …
А) -27 ; Б) 27 ; В) -9 ; Г) 9
1.9. Який кут утворюють стрілки годинника о 16 годині?
А) 130° ; Б) 120° ; В) 110° ; Г) 100°
1.10. Один з кутів паралелограма дорівнює 60°. Знайти решту його кутів.
А) 60° , 60° , 60° ; Б) 150° , 30° , 30° ; В) 120° , 60° , 120° ; Г) 100° , 100° , 60°
1.11. У трикутнику ![]() . Яка сторона трикутника є найбільшою?
. Яка сторона трикутника є найбільшою?
А) неможливо визначити; Б) АВ ; В) АС ; Г) ВС
1.12. При якому значенні ![]() вектори
вектори ![]() перпендикулярні?
перпендикулярні?
А) -1 ; Б) 1 ; В) 3 ; Г) 9
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть: ![]()
2.2. Знайдіть точки параболи, що є графіком функції ![]() , у яких абсциси й ординати рівні між собою.
, у яких абсциси й ординати рівні між собою.
2.3. Розв’яжіть систему рівнянь: 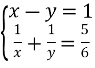
2.4. Знайдіть радіус круга, якщо площа сектора цього круга дорівнює 20π см2, а центральний кут, що відповідає цьому сектору, дорівнює 72°.
Частина третя
3.1. За 4 футбольних і 3 волейбольних м’ячі заплатили 320 грн. Після того як футбольний м’яч подешевшав на 20%, а волейбольний подорожчав на 5%, за 2 футбольних й 1 волейбольний м’ячі заплатили 122 грн. Яка була початкова ціна кожного м’яча?
3.2. Розв’яжіть рівняння: ![]()
3.3. Дві сторони трикутника дорівнюють 7 см і 11 см, а медіана, проведена до третьої сторони, на 8 см менша за цю сторону. Знайдіть невідому сторону трикутника.
ВАРІАНТ 6
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Запишіть:
 м + 35 см у сантиметрах.
м + 35 см у сантиметрах.
А) 40 см ; Б) 55 см ; В) 37 см ; Г) ![]() см
см
1.2. Знайдіть різницю : ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.3. Спростіть вираз: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Знайдіть точку перетину графіка функції ![]() з віссю абсцис.
з віссю абсцис.
А) (-4 ; 0) ; Б) (0 ; 4) ; В) (0 ; -20) ; Г) (4 ; 0)
1.5. Піднесіть до степеня 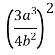
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Звільніться від ірраціональності в знаменнику дробу: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
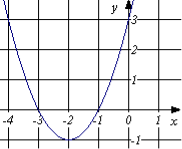 1.7. На рисунку зображено графік функції
1.7. На рисунку зображено графік функції ![]() . Укажіть найменше значення функції.
. Укажіть найменше значення функції.
А) 0 ; Б) -1 ; В) -2 ; Г) -3
1.8. Протягом восьмигодинного робочого дня робітник щогодини виготовляв 12; 10; 8; 11; 9; 12; 10; 8 деталей. Знайдіть середнє значення даної вибірки.
А) 9 ; Б) 10 ; В) 11 ; Г) 12
1.9. Один із суміжних кутів у 4 рази більший за другий. Знайдіть градусну міру меншого з кутів.
А) 36° ; Б) 144° ; В) 45° ; Г) 135°
1.10. Основи трапеції дорівнюють 4 см і 10 см. Знайдіть її середню лінію.
А) 7 см ; Б) 14 см ; В) 3,5 см ; Г) 6 см.
1.11. Визначте кутовий коефіцієнт прямої, заданої рівнянням ![]() .
.
А) 3 ; Б) 1 ; В) -1 ; Г) -3
1.12. Знайдіть площу трикутника, сторони якого дорівнюють 13 дм, 14 дм, 15 дм.
А) ![]() дм2 ; Б)
дм2 ; Б) ![]() дм2 ; В) 42 дм2 ; Г) 84 дм2
дм2 ; В) 42 дм2 ; Г) 84 дм2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. Задайте формулою лінійну функцію, графік якої проходить через точки (1 ; -5) і (-3 ; -13).
2.3. Знайдіть суму нескінченої геометричної прогресії ![]() , якщо
, якщо ![]()
2.4. У трикутнику ![]() . Знайдіть кут С.
. Знайдіть кут С.
Частина третя
3.1. Потяг мав проїхати 300 км. Проїхавши ![]() шляху, він зупинився на 1 год, а потім продовжив рух із швидкістю на 10 км/год меншою за початкову. Знайдіть швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду.
шляху, він зупинився на 1 год, а потім продовжив рух із швидкістю на 10 км/год меншою за початкову. Знайдіть швидкість потяга до зупинки, якщо в пункт призначення він прибув через 8 год після виїзду.
3.2. Знайдіть цілі розв’язки системи нерівностей 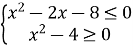
3.3. У ромбі висота, що проведена з вершини тупого кута, ділить сторону навпіл. Знайдіть площу ромба, якщо його більша діагональ дорівнює ![]() см.
см.
ВАРІАНТ 7
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Розв’яжіть рівняння:
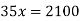
А) 6 ; Б) 73500 ; В) 7350 ; Г) 60
1.2. Виконайте ділення: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.3. Подайте добуток ![]() у вигляді многочлена.
у вигляді многочлена.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Розв’яжіть рівняння: ![]()
А) -3 і 4 ; Б) 12 ; В) 3 і -4 ; Г) -12
1.5. Запишіть число 328 000 000 у стандартному вигляді.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Піднесіть до степеня: 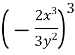
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. Яке із чисел є розв’язком нерівності: ![]() ?
?
А) 2 ; Б) -2 ; В) -1 ; Г) 1
1.8. Знайдіть нулі функції: ![]()
А) -5 ; Б) 0 ; В) 5 ; Г) 0 ; -5
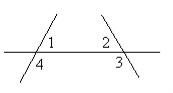 1.9. За рисунком назвіть пару кутів, які є внутрішніми різносторонніми.
1.9. За рисунком назвіть пару кутів, які є внутрішніми різносторонніми.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
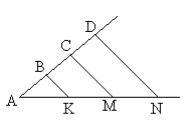 1.10. На рисунку AB = BC = CD = 5 см, BK || CM || DN , AK = 7 см. Знайдіть довжину відрізка MN.
1.10. На рисунку AB = BC = CD = 5 см, BK || CM || DN , AK = 7 см. Знайдіть довжину відрізка MN.
А) 8 см ; Б) 7 см ; В) 5 см ; Г) 6 см
1.11. Довжина кола дорівнює 6π см. Знайдіть його радіус.
А) ![]() см ; Б)
см ; Б) ![]() см ; В) 3 см ; Г) 6 см
см ; В) 3 см ; Г) 6 см
1.12. Знайдіть площу ромба, периметр якого дорівнює ![]() см, а один з кутів 135°.
см, а один з кутів 135°.
А) ![]() см2 ; Б)
см2 ; Б) ![]() см2 ; В) 8 см2 ; Г) 16 см2
см2 ; В) 8 см2 ; Г) 16 см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Виконайте множення: ![]()
2.2. Складіть квадратне рівняння з цілими коефіцієнтами, корені якого дорівнюють числам: ![]() і 5.
і 5.
2.3. Вкладник поклав до банку 10000 гривень під 16% річних. Скільки відсоткових грошей матиме вкладник через два роки?
2.4. У ![]() . Знайдіть довжину меншого катета трикутника.
. Знайдіть довжину меншого катета трикутника.
Частина третя
3.1. Сплав золота зі сріблом містить 20 г золота. До цього сплаву додали 5 г срібла і 10 г золота. Отриманий сплав містить на 5% більше срібла, ніж початковий. Скільки грамів срібла було в початковому сплаві?
3.2. Яка ймовірність того, що навмання вибране двоцифрове натуральне число кратне 4?
3.3. Точка дотику кола, вписаного у прямокутний трикутник, ділить гіпотенузу на відрізки 4 см і 6 см. Знайдіть периметр трикутника.
ВАРІАНТ 8
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Знайдіть різницю:
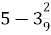
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.2. Серед наведених записів укажіть правильну пропорцію.
А) 18 : 2 = 6 : 3 ; Б) 25 : 20 = 10 : 2 ; В) 12 : 3 = 27 : 9 ; Г) 2 : 6 = 3 : 9
1.3. Знайдіть значення функції ![]() , що відповідає значенню аргументу 3.
, що відповідає значенню аргументу 3.
А) -2,5 ; Б) -2 ; В) 2,5 ; Г) 2
1.4. Подайте у вигляді квадрата двочлена вираз ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Знайдіть область визначення функції ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Який шлях подолає світло за ![]() с , якщо швидкість світла дорівнює
с , якщо швидкість світла дорівнює ![]() м/с?
м/с?
А) ![]() м ; Б)
м ; Б) ![]() м ; В)
м ; В) ![]() км ; Г)
км ; Г) ![]() м
м
1.7. З чисел 2 ; 4 ; 6 ; 8 ; 10 навмання вибрали одне число. Яка ймовірність того, що буде вибрано число 4?
А) 1 ; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.8. Яка з нерівностей є правильною за будь-якого значення ![]() ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
 1.9. Знайдіть бічну сторону рівнобедреного трикутника, якщо його периметр дорівнює 58 см, а основа дорівнює 18 см.
1.9. Знайдіть бічну сторону рівнобедреного трикутника, якщо його периметр дорівнює 58 см, а основа дорівнює 18 см.
А) 44 см ; Б) 20 см ; В) 22 см ; Г) 40 см
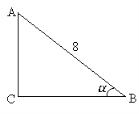
1.10. Користуючись рисунком, знайдіть сторону ВС трикутника АВС.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.11. Запишіть рівняння прямої, яка паралельна осі ![]() і проходить через точку (2 ; 1).
і проходить через точку (2 ; 1).
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г) y
; Г) y ![]()
1.12. Знайдіть кількість сторін правильного многокутника, зовнішній кут якого дорівнює 60°.
А) 5 сторін ; Б) 6 сторін ; В) 8 сторін ; Г) 7 сторін
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Розв’яжіть систему нерівностей: 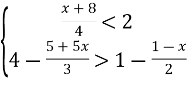
2.3. Побудуйте графік функції ![]() . У бланк відповідей запишіть найбільше значення функції.
. У бланк відповідей запишіть найбільше значення функції.
2.4. Модуль вектора ![]() дорівнює 5. Знайдіть
дорівнює 5. Знайдіть ![]() .
.
Частина третя
3.1. Рибалка відправився на човні з пукту A проти течії річки. Пропливши 3 км, він кинув весла, і через 4 год 30 хв після відправлення з пункту A течія його віднесла до цього пункту. Знайдіть швидкість течії, якщо швидкість човна у стоячій воді дорівнює 2,7 км/год.
3.2. Розв’яжіть рівняння ![]()
3.3. Сторони трикутника дорівнюють ![]() см і 2 см. Знайдіть третю сторону трикутника, якщо вона дорівнює радіусу кола, описаного навколо цього трикутника.
см і 2 см. Знайдіть третю сторону трикутника, якщо вона дорівнює радіусу кола, описаного навколо цього трикутника.
ВАРІАНТ 9
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Знайдіть 25% від числа 500.
А) 375 ; Б) 12,5 ; В) 37,5 ; Г) 125
1.2. Спростіть вираз: ![]()
А) 2,1 ; Б) ![]() ; В)
; В) ![]() ; Г) 3,1
; Г) 3,1
1.3. Яке з поданих рівнянь має розв’язок (2 ; -1)?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Укажіть рівняння, яке рівносильне рівнянню ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Знайдіть дискримінант квадратного рівняння: ![]()
А) 1 ; Б) -1 ; В) 0 ; Г) ![]()
1.6. Скоротіть дріб: ![]()
А) ![]() ; Б) 5 ; В)
; Б) 5 ; В) ![]() ; Г)
; Г) ![]()
1.7. Дано арифметичну прогресію ![]() . Знайдіть
. Знайдіть ![]() , якщо
, якщо ![]()
А) 10 ; Б) -12 ; В) -10 ; Г) -14
1.8. Яка з нерівностей є правильною, якщо ![]() ?
?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.9. Укажіть геометричне місце точок, розміщених на відстані 5 см від даної точки А.
А) коло ; Б) круг ; В) пряма ; Г) відрізок
1.10. У ромбі сторона дорівнює 8 см, а більша діагональ 12 см. Знайдіть меншу діагональ ромба.
А) ![]() см ; Б)
см ; Б) ![]() см ; В)
см ; В) ![]() см; Г) 10 см
см; Г) 10 см
1.11. Обчисліть: ![]() , якщо
, якщо ![]()
А) ![]() ; Б)
; Б) ![]() ; В) 10 ; Г)
; В) 10 ; Г) ![]()
1.12. Визначте вид трикутника, сторони якого дорівнюють 13 см, 12 см і 5 см.
А) визначити неможливо; Б) прямокутний; В) гострокутний; Г) тупокутний
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спостіть вираз: ![]()
2.2. Скоротіть дріб: ![]()
2.3. Знайдіть цілі розв’язки нерівності: ![]()
2.4. Точки А(4; -2) , В(-2; 6) , С(-6; 10) – вершини паралелограма ABCD. Знайдіть координати вершини D цього паралелограма.
Частина третя
3.1. Потроєна сума цифр двоцифрового натурального числа дорівнює самому числу. Якщо поміняти місцями його цифри, то отримаємо число, яке більше за дане на 45. Знайдіть дане число.
3.2. Доведіть, що вираз 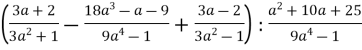
набуває від’ємних значень для всіх ![]() .
.
3.3. Сторони трикутника дорівнюють відповідно 11 см, 12 см, 13 см. Знайти медіану, яку проведено до більшої сторони трикутника.
ВАРІАНТ 10
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Запишіть найменше чотирицифрове число, у запису якого використано цифри 9; 5; 0; 3, що не повторюються.
А) 3095 ; Б) 3590 ; В) 3059 ; Г) 3509 .
1.2. Яке число є кратним числу 24?
А) 6 ; Б) 2 ; В) 12 ; Г) 72
1.3. Коренем якого рівняння є число 7?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ?
?
1.4. Яка з поданих систем рівнянь не має розв’язку?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Скоротіть дріб: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Яке з рівнянь не має коренів?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Розв’яжіть нерівність: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Знайдіть суму п’яти перших членів арифметичної прогресії ![]() , якщо
, якщо ![]()
А) -10 ; Б) -5 ; В) -4 ; Г) 20
1.9. Промінь ![]() проходить між сторонами
проходить між сторонами ![]() так, що
так, що ![]() на 18° менший від
на 18° менший від ![]() . Знайдіть градусну міру
. Знайдіть градусну міру ![]() і
і ![]() .
.
А) 19° і 37° ; Б) 10° і 46° ; В) 37° і 19° ; Г) 12° і 44°
1.10. Який з чотирикутників завжди має рівні діагоналі?
А) Прямокутник ; Б) Ромб ; В) Трапеція ; Г) Паралелограм
1.11. Знайдіть радіус кола, описаного навколо трикутника АВС, якщо ![]()
А) ![]() см ; Б)
см ; Б) ![]() см ; В) 3 см ; Г) 6 см
см ; В) 3 см ; Г) 6 см
1.12. Знайдіть довжину вектора ![]() , якщо А(3 ; -1) , В(3 ; -4)
, якщо А(3 ; -1) , В(3 ; -4)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г) 3
; Г) 3
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. При якому значенні ![]() віссю симетрії параболи, що є графіком функції
віссю симетрії параболи, що є графіком функції ![]() , є пряма
, є пряма ![]() ?
?
2.3. Розв’яжіть систему рівнянь: ![]()
2.4. У прямокутній трапеції менша основа та менша бічна сторона дорівнюють 8 см, а більша бічна сторона – 10 см. Знайдіть площу трапеції.
Частина третя
3.1. Один оператор комп’ютерного набору повинен набрати рукопис, що складається зі 120 сторінок, а другий – зі 100 сторінок. Перший щогодини набирає на 1 сторінку більше, ніж другий. Скільки сторінок набирає щогодини кожний з операторів, якщо перший закінчив роботу на 1 год швидше, ніж другий?
3.2. Побудуйте графік функції 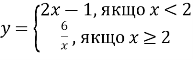 Користуючись побудованим графіком, знайдіть область значень функції.
Користуючись побудованим графіком, знайдіть область значень функції.
3.3. Знайдіть площу прямокутного трикутника, якщо бісектриса його гострого кута ділить протилежний катет на відрізки завдовжки 3 см і 5 см.
ВАРІАНТ 11
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Порівняйте величини: 24 хв та
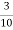 год.
год.
А) 24 хв ![]() год ; Б) 24 хв
год ; Б) 24 хв ![]() год ; В) 24 хв
год ; В) 24 хв ![]() год ; Г) 24 хв <
год ; Г) 24 хв <![]() год
год
1.2. Знайдіть суму: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.3. Який з виразів є многочленом стандартного вигляду?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. На якому з рисунків зображено графік функції ![]() ?
?
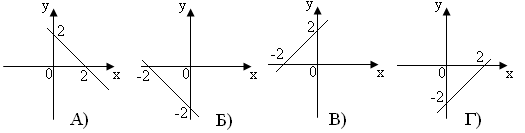
1.5. Виконайте ділення: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Скоротіть дріб: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. Знайдіть координати вершини параболи ![]()
А) (-1 ; 0) ; Б) (-4 ; 1) ; В) (1 ; -4) ; Г) (0 ; -1)
1.8. У коробці лежать 5 зелених, 7 жовтих і 3 червоних кульки. Яка ймовірність того, що навмання витягнута з коробки кулька буде не зеленого кольору?
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.9. Яка градусна міра кута, якщо суміжний з ним кут дорівнює 110°?
А) 110° ; Б) 10°; В) 90° ; Г) 70°
1.10. Знайдіть середню лінію рівнобічної трапеції, якщо її бічна сторона дорівнює 6 см, а периметр – 48 см.
А) 18 см ; Б) 36 см ; В) 19 см ; Г) 16 см
1.11. У трапеції діагоналі дорівнюють 8 см і ![]() см, а кут між ними - 30°. Знайдіть площу трапеції.
см, а кут між ними - 30°. Знайдіть площу трапеції.
А) 60 см2 ; Б) 30 см2 ; В) ![]() см2 ; Г)
см2 ; Г) ![]() см2
см2
1.12. Знайдіть координати точки перетину прямих ![]()
А) (3 ; 1) ; Б) (1 ; 3) ; В) (-3 ; -1) ; Г) (-1 ; 3)
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. Побудуйте графік функції ![]() . У бланк відповідей запишіть значення
. У бланк відповідей запишіть значення ![]() , при яких функція набуває значень, більших за 4.
, при яких функція набуває значень, більших за 4.
2.3. Між числами 8 і -1 вставте два числа, щоб вони разом з даними утворили арифметичну прогресію.
2.4. У трикутнику ![]() кут С – тупий. ВС = 15 см; АВ = 20 см; ВК – висота трикутника; ВК = 12 см. Знайдіть сторону АС.
кут С – тупий. ВС = 15 см; АВ = 20 см; ВК – висота трикутника; ВК = 12 см. Знайдіть сторону АС.
Частина третя
3.1. Із двох міст, відстань між якими 24 км, назустріч один одному вирушили два пішоходи і зустрілися на середині шляху, причому один з них вийшов на одну годину раніше за іншого. Якби пішоходи вийшли одночасно, то вони зустрілися б через 2 год 24 хв. Знайдіть швидкості пішоходів.
3.2. Спростіть вираз ![]() .
.
3.3. Бісектриса кута прямокутника ділить його діагональ у відношені 2:7. Знайдіть площу прямокутника, якщо його периметр дорівнює 108 см.
ВАРІАНТ 12
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Знайдіть корінь рівняння:
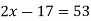
А) 35 ; Б) 40 ; В) 18 ; Г) 72
1.2. Виконайте множення: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г) 6
; Г) 6
1.3. Які вирази є тотожно рівними?
А) ![]() ; Б)
; Б) ![]() ;
;
В) ![]() ; Г)
; Г) ![]()
1.4. Запишіть одночлен ![]() в стандартному вигляді:
в стандартному вигляді:
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.5. Обчисліть значення виразу : ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Виконайте ділення: ![]()
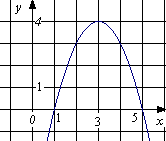 А)
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. На рисунку зображено графік функції ![]() . Знайдіть множину розв’язків нерівності
. Знайдіть множину розв’язків нерівності ![]() .
.
А) ![]() ; Б)
; Б) ![]() ;
;
В) (1; 5) ; Г) [1 ; 5]
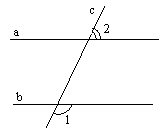 1.8. Вершина якої з парабол належить осі ординат?
1.8. Вершина якої з парабол належить осі ординат?
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
1.9. На рисунку зображено паралельні прямі ![]() , які перетинає січна
, які перетинає січна ![]() . Користуючись рисунком, знайдіть
. Користуючись рисунком, знайдіть ![]() , якщо
, якщо ![]() .
.
А) 140° ; Б) 40° ; В) 130° ; Г) 50°
1.10. Знайдіть вписаний кут, який спирається на дугу, що становить ![]() кола.
кола.
А) 15° ; Б) 30° ; В) 120° ; Г) 60°
1.11. Радіус кола дорівнює ![]() см. Знайдіть сторону правильного трикутника, описаного навколо цього кола.
см. Знайдіть сторону правильного трикутника, описаного навколо цього кола.
А) ![]() см ; Б)
см ; Б) ![]() см; В) 12 см ; Г) 6 см
см; В) 12 см ; Г) 6 см
1.12. У рівнобедреному трикутнику основа дорівнює 12 см, а бічна сторона – 10 см. Знайдіть площу трикутника.
А) 48 см2 ; Б) 96 см2 ; В) 120 см2 ; Г) 60 см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть значення виразу ![]() , якщо
, якщо ![]()
2.2. Один з коренів квадратного тричлена ![]() дорівнює 5. Знайдіть
дорівнює 5. Знайдіть ![]() і другий корінь тричлена.
і другий корінь тричлена.
2.3. У коробці лежить 16 синіх кульок і кілька червоних. Скільки червоних кульок у коробці, якщо ймовірність витягнути навмання червону кульку дорівнює ![]() ?
?
2.4. Знайдіть тупий кут ромба, якщо його сторона утворює з діагоналями кути, різниця яких дорівнює 20°.
Частина третя
3.1. Для наповнення басейну через першу трубу потрібно стільки само часу, що й для наповнення через другу і третю трубу одночасно. Скільки часу потрібно для наповнення басейну окремо кожною трубою, якщо через першу наповнюють басейн на 2 год швидше, ніж через третю, і на 8 год швидше, ніж через другу?
3.2. Розв’яжіть рівняння ![]() .
.
3.3. Основи рівнобічної трапеції дорівнюють 6 см і 10 см, а діагональ ділить навпіл тупий кут трапеції. Знайдіть довжину цієї діагоналі.
ВАРІАНТ 13
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Яку частину години становить 17 хв?
А) ![]() год ; Б)
год ; Б) ![]() год ; В)
год ; В) ![]() год ; Г)
год ; Г) ![]() год
год
1.2. Відстань між містами на карті 6,4 см. Знайдіть відстань між містами на місцевості, якщо масштаб карти 1 : 2 000 000.
А) 32 км ; Б) 128 км ; В) 3.2 км ; Г) 12,8 км
1.3. Укажіть функцію, яка не є лінійною функцією.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.4. Подайте добуток ![]() у вигляді многочлена.
у вигляді многочлена.
А) ![]() ; Б)
; Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Обчисліть значення виразу: ![]()
А) 10 ; Б) -10 ; В) -5 ; Г) -40
1.6. Спростіть вираз: 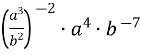
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.7. З 20 кг насіння соняшнику можна отримати 3.5 кг олії. Скільки олії можна одержати з 400 кг такого самого насіння?
А) 17,5 кг ; Б) 7 кг ; В) 175 кг ; Г) 70 кг
1.8. Розв’яжіть нерівність : ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
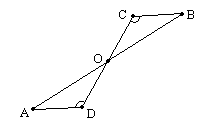 1.9. За якими елементами рівні трикутники
1.9. За якими елементами рівні трикутники ![]() (див. рис.), якщо
(див. рис.), якщо ![]() і
і ![]() ?
?
А) за стороною і двома прилеглими кутами;
Б) за трьома сторонами;
В) за двома сторонами і кутом між ними;
Г) визначити неможливо.
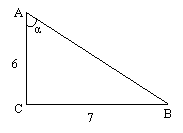 1.10. У прямокутному трикутнику з кутом
1.10. У прямокутному трикутнику з кутом ![]() та катетами 6 см і 7 см знайдіть
та катетами 6 см і 7 см знайдіть ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.11. Знайдіть рівняння кола з центром у точці О(-2 ; 1) та радіусом, що дорівнює 4.
А) ![]() ; Б)
; Б) ![]() ;
;
В) ![]() ; Г)
; Г) ![]()
1.12. Знайдіть площу кругового сектора радіуса 5 см, центральний кут якого дорівнює 72°
А) 20π см2 ; Б) 10π см2 ; В) 5π см2 ; Г) π см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Знайдіть найбільше ціле значення ![]() , при якому різниця дробів
, при якому різниця дробів ![]() є додатною.
є додатною.
2.3. Побудуйте графік функції ![]() . У бланк відповідей запишіть область значень функції.
. У бланк відповідей запишіть область значень функції.
2.4. У рівнобічній трапеції бічна сторона дорівнює меншій основі, а діагональ утворює з цією основою кут 30°. Знайдіть гострий кут трапеції.
Частина третя
3.1. У двох ящиках знаходяться кольорові кульки. Якщо з другого ящика перекласти до першого 10 кульок, то в обох ящиках кульок стане порівну. Якщо ж з першого ящика перекласти до другого 20 кульок, то в першому ящику кульок залишиться у 4 рази менше, ніж у другому. Скільки кульок лежить у кожному ящику?
3.2. При яких значеннях a рівняння ![]() має один корінь?
має один корінь?
3.3. Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки завдовжки 15 см і 20 см. Знайдіть радіус кола, вписаного у трикутник.
ВАРІАНТ 14
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Обчисліть : 23,8 – (3,45 + 2, 17)
А) 18,18 ; Б) 18,22 ; В) 22,52 ; Г) 22,62
1.2. Зведіть подібні доданки у виразі: ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.3. Яка пара чисел є розв’язком системи: ![]() ?
?
А) (-3 ;2) ; Б) (3 ;2) ; В) (-2 ;3) ; Г) (2 ;3)
1.4. Розв’яжіть рівняння: ![]()
А) 0,75 ; Б) 0 ; В) -3 ; Г) 3
1.5. Виконайте додавання : ![]()
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
1.6. Знайдіть корені квадратного рівняння: ![]()
А) 2 ; 3 Б) -6 ; 1 В) -1 ; 6 Г) -2 ; -3
1.7. Дано геометричну прогресію ![]() . Знайдіть
. Знайдіть ![]() , якщо
, якщо ![]()
А) -2 ; Б) 2 ; В) -4 ; Г) 4
1.8. Довжина сторони рівностороннього трикутника дорівнює ![]() дм. Оцініть значення його периметра
дм. Оцініть значення його периметра ![]() , якщо
, якщо ![]() .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]()
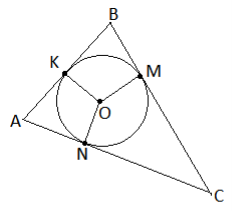 1.9. На рисунку точки дотику кола з центром у точці O і сторін різностороннього трикутника ABC позначено відповідно
1.9. На рисунку точки дотику кола з центром у точці O і сторін різностороннього трикутника ABC позначено відповідно ![]() . Укажіть відрізок, що дорівнює відрізку
. Укажіть відрізок, що дорівнює відрізку ![]() .
.
А) КО ; Б) МС ; В) МВ ; Г) AN
1.10. Сторони прямокутника дорівнюють 16 см і 12 см. Знайдіть довжину діагоналі прямокутника.
А) 40 см ; Б) 20 см ; В) ![]() см ; Г)
см ; Г) ![]() см
см
1.11. Знайдіть координати вектора, який є сумою векторів ![]()
А) (1 ; -3) ; Б) (5 ;-5) ; В) (1 ; -5) ; Г) (-5 ; 5)
1.12. Сторони паралелограма дорівнюють 5 см і ![]() см, а один з кутів дорівнює
см, а один з кутів дорівнює ![]() . Знайдіть більшу діагональ паралелограма.
. Знайдіть більшу діагональ паралелограма.
А) ![]() см ; Б)
см ; Б) ![]() см ; В)
см ; В) ![]() см ; Г)
см ; Г) ![]() см
см
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Виконайте додавання ![]() , подайте відповідь у стандартному вигляді.
, подайте відповідь у стандартному вигляді.
2.2. Внесіть множник під знак кореня у виразі ![]() , якщо
, якщо ![]()
2.3. Знайдіть натуральні розв’язки системи нерівностей: ![]()
2.4. О – точка перетину діагоналей трапеції ABCD з основами AD i BC, AD = 9 см, ВС = 6 см. Знайдіть відрізки DO i BO , якщо їх різниця дорівнює 2 см.
Частина третя
3.1. Знайдіть п’ять послідовних парних натуральних чисел, коли відомо, що сума квадратів трьох перших чисел дорівнює сумі квадратів двох останніх.
3.2. Спростіть вираз ![]() .
.
3.3. Центр кола, описаного навколо трапеції, лежить на її більшій основі. Знайдіть радіус цього кола, якщо діагональ трапеції дорівнює 20 см, а її висота – 12 см.
ВАРІАНТ 15
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Обчисліть значення виразу (1865 – 365) : 50
А) 75000 ; Б) 300 ; В) 7500 ; Г) 30
1.2. Знайдіть найбільший спільний дільник чисел: 72 і 48
А) 8 ; Б) 24 ; В) 12 ; Г) 48
1.3. Яке з рівнянь має безліч розв’язків?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Графік якого рівняння проходить через точку А(2 ; -2) ?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Виконайте додавання: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Складіть зведення квадратне рівняння, корені якого дорівнюють: 5 і -3.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Порівняйте числа ![]() , якщо
, якщо ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Знайдіть перший член геометричної прогресії ![]() , якщо
, якщо ![]()
А) ![]() ; Б) -4 ; В) 2 ; Г) 4
; Б) -4 ; В) 2 ; Г) 4
1.9. Довжина відрізка АВ = 84 см. На відрізку дано точку М, що поділяє його на два відрізки, причому АМ менший за ВМ у 3 рази. Знайдіть довжину відрізка ВМ.
А) 63 см ; Б) 56 см ; В) 42 см ; Г) 28 см
1.10. Довжини сторін паралелограма відносяться як 3 : 4, а його периметр дорівнює 70 см. Знайдіть сторони паралелограма.
А) 15 см; 20 см; 15 см; 20 см Б) 60 см; 80 см; 60 см; 80 см
В) 5 см; 5 см; 5 см; 5 см Г) 30 см; 40 см; 30 см; 40 см
1.11. Дві сторони трикутника дорівнюють 6 дм і 8 дм, а кут між ними - 60°. Знайдіть невідому сторону трикутника.
А) ![]() дм ; Б)
дм ; Б) ![]() дм ; В)
дм ; В) ![]() дм ; Г)
дм ; Г) ![]() дм
дм
1.12. Знайдіть координати вектора ![]() , якщо
, якщо ![]()
А) (-7 ; -9) Б) (-7 ; 9) В) (7 ; -9) Г) (7 ; 9)
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть: ![]()
2.2. Графіком квадратичної функції є парабола, що має вершину у початку координат і проходить через точку А(2 ; -8). Задайте цю функцію формулою.
2.3. Розв’яжіть систему рівнянь: ![]()
2.4. Зовнішній кут правильного многокутника становить ![]() внутрішнього. Знайдіть кількість сторін цього многокутника.
внутрішнього. Знайдіть кількість сторін цього многокутника.
Частина третя
3.1. Із пункту A в пункт B, відстань між якими дорівнює 180 км, одночасно виїхали два автомобілі. Через 2 години виявилося, що перший проїхав на 20 км більше, ніж другий. Знайдіть швидкість кожного автомобіля, коли відомо, що на весь шлях перший затратив на 15 хв менше, ніж другий.
3.2. Знайдіть найменший член послідовності , що задана формулою n-го члена ![]() .
.
3.3. Навколо трапеції, основи якої дорівнюють 12 см і 16 см, а висота – 14 см, описано коло. Знайдіть довжину цього кола.
ВАРІАНТ 16
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Знайдіть різницю: 16 кг 300 г – 8 кг 500 г
А) 6 кг 800 г Б) 8 кг 200 г В) 7 кг 800 г Г) 8 кг 800 г
1.2. Знайдіть суму: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.3. Перетворіть у многочлен вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Графіком якої з функцій є пряма, паралельна графіку функції ![]() ?
?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Виконайте множення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Обчисліть значення виразу: ![]()
А) 7 ; Б) -1 ; В) ![]() Г)
Г) ![]()
1.7. Знайдіть координати точки перетину графіка функції ![]() з віссю абсцис.
з віссю абсцис.
А) (3 ; 0) Б) (0 ; 15) В) (-3 ;0) Г) (0 ; 3)
1.8. Який відсотковий вміст заліза в руді, якщо 300 т залізної руди містить 24 т заліза?
 А) 87,5 % ; Б) 12,5 % ; В) 92 % ; Г) 8 %
А) 87,5 % ; Б) 12,5 % ; В) 92 % ; Г) 8 %
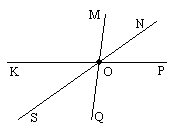
1.9. На рисунку ![]() . Знайдіть градусну міру
. Знайдіть градусну міру ![]() .
.
А) 30° ; Б) 70° ; В) 100° ; Г) 130°
1.10. Гострий кут прямокутної трапеції в 3 рази менший від тупого кута. Знайдіть ці кути.
А) 60° і 120° Б) 45° і 135° В) 30° і 60° Г) 10° і 30°
1.11. У прямокутному трикутнику один з катетів дорівнює 4 дм, а гіпотенуза – 5 дм. Знайдіть площу трикутника.
А) 20 дм2 ; Б) 10 дм2 ; В) 10 дм2 ; Г) 6 дм2
1.12. Точка С – середина відрізка АВ. Знайдіть координати точки В, якщо А(-3;-2), С(1; -3)
А) (-2 ; -5) Б) (-1 ; -25) В) (5 ; -4) Г) (-5 ; 4)
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. На прямій ![]() знайдіть точку, ордината якої удвічі більша за абсцису.
знайдіть точку, ордината якої удвічі більша за абсцису.
2.3. Знайдіть суму перших семи членів геометричної прогресії ![]() , якщо
, якщо ![]()
2.4. Дві сторони трикутника відносяться як 5 : 3, а кут між ними дорівнює 120°. Знайдіть третю сторону трикутника, якщо його периметр дорівнює 45 см.
Частина третя
3.1. Два трактористи зорали поле за 12 год спільної роботи. За скільки годин може зорати це поле кожний тракторист окремо, якщо перший може це зробити на 10 год швидше, ніж другий?
3.2. При яких значеннях m нерівність ![]() виконується для всіх дійсних значень х?
виконується для всіх дійсних значень х?
3.3. Катети прямокутного трикутника дорівнюють 18 см і 24 см. Знайдіть бісектрису трикутника, проведену з вершини його меншого гострого кута.
ВАРІАНТ 17
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Розв’яжіть рівняння:
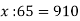
А) 14 ; Б) 5915 ; В) 131 ; Г) 59 150
1.2. Виконайте множення : ![]()
А) 50 ; Б) ![]() ; В) 56 ; Г) 14
; В) 56 ; Г) 14
1.3. Подайте у вигляді многочлена вираз : ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Розкладіть на множники вираз : ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Спростіть вираз : ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Виконайте множення : ![]()
А) -3 Б) ![]() В)
В) ![]() Г) 3
Г) 3
1.7. Для якої нерівності число -2 є розв’язком?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г)![]()
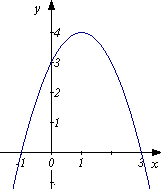 1.8. Укажіть формулу, що задає функцію, графік якої зображено на рисунку.
1.8. Укажіть формулу, що задає функцію, графік якої зображено на рисунку.
А) ![]()
Б) ![]()
В) ![]()
Г) ![]()
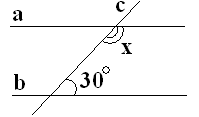 1.9. На рисунку зображено паралельні прямі
1.9. На рисунку зображено паралельні прямі ![]() , які перетинає січна с. Користуючись рисунком знайдіть кут
, які перетинає січна с. Користуючись рисунком знайдіть кут ![]()
А) 70° Б) 150° В) 60° Г) 120°
1.10. навколо кола описано чотирикутник ABCD, у якого АВ = 7 см , ВС = 8 см , AD = 9 см. Знайдіть довжину сторони CD.
А) 3,5 см Б) 7 см В) 14 см Г) 10 см
1.11. Діагональ квадрата дорівнює ![]() см. Чому дорівнює радіус описаного кола навколо квадрата?
см. Чому дорівнює радіус описаного кола навколо квадрата?
А) ![]() см Б)
см Б) ![]() см В) 3 см Г) 6 см
см В) 3 см Г) 6 см
1.12. Знайдіть площу паралелограма, у якого діагоналі дорівнюють 8 см і 10 см, а тупий кут між ними 150°.
А) ![]() см2 Б) 40 см2 В) 20 см2 Г)
см2 Б) 40 см2 В) 20 см2 Г) ![]() см2
см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз : ![]()
2.2. Обчисліть значення виразу : ![]() , якщо
, якщо ![]()
2.3. У бригаді було 5 робітників, середній вік яких становив 35 років. Після того як бригада поповнилась одним робітником, середній вік робітників став 34 роки. Скільки років робітнику, який поповнив бригаду?
2.4. У ![]() . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
Частина третя
3.1. Деяке двоцифрове натуральне число в 4 рази більше за суму і втричі більше за добуток своїх цифр. Знайдіть це число.
3.2. Доведіть, що коли a, b і c – три послідовних члени арифметичної прогресії, то ![]() .
.
3.3. У трикутнику ABC АМ – медіана. На стороні AB трикутника ABC позначили точку K так, що AK : KB = 2 : 3. У якому відношенні медіана АМ ділить відрізок СК?
ВАРІАНТ 18
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Скільки градусів становлять
 розгорнутого кута?
розгорнутого кута?
А) 54° Б) 108° В) 150° Г) 118°
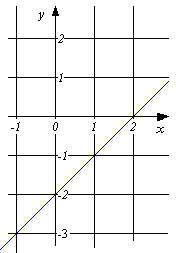 1.2. Знайдіть невідомий член пропорції :
1.2. Знайдіть невідомий член пропорції : ![]()
А) 6,25 Б) ![]() В) 16 Г) 4
В) 16 Г) 4
1.3. Користуючись графіком, знайдіть значення функції, якщо аргумент дорівнює -1.
А) -3 Б) -1 В) 0 Г) 1
1.4. Розкладіть многочлен ![]()
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
1.5. Розв’яжіть рівняння: ![]()
А) ![]() Б) 5 В) -5 ; 5 Г) 25
Б) 5 В) -5 ; 5 Г) 25
1.6. Знайдіть значення виразу: ![]()
А) 1 Б) -2 В) ![]() Г)
Г) ![]()
1.7. Який відсоток жирності молока, якщо з 250 кг молока отримали 15 кг жиру?
А) 6 % Б) 60 % В) 160 % Г) 94 %
1.8. Розв’яжіть нерівність: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. У трикутнику ![]() . Знайдіть градусну міру зовнішнього кута при вершині А.
. Знайдіть градусну міру зовнішнього кута при вершині А.
А) 143° Б) 37° В) 137° Г) 100°
1.10. У прямокутному трикутнику один з катетів дорівнює 4 см, а косинус прилеглого кута 0,8. Знайдіть гіпотенузу.
А) 7 см Б) 6 см В) 5 см Г) 3 см
1.11. Знайдіть відстань від точки М( -2 ; -3) до осі ординат.
А) 2 Б) -3 В) 3 Г) -2
1.12. Яка градусна міра дуги кола, радіус якого становить 6 см, а довжина дуги дорівнює π см ?
А) 60° Б) 30° В) 45° Г) 15°
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Знайдіть значення виразу : ![]() , якщо
, якщо ![]()
2.2. Знайдіть цілі розв’язки системи нерівностей: 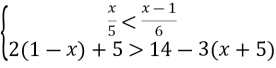
2.3. Побудуйте графік функції: ![]() . У бланк відповідей запишіть проміжок зростання функції.
. У бланк відповідей запишіть проміжок зростання функції.
2.4. Сторони чотирикутника відносяться як 2 : 3 : 3 : 4. Знайдіть периметр подібного йому чотирикутника, найбільша сторона якого дорівнює 20 см.
Частина третя
3.1. Один оператор комп’ютерного набору набирав певний рукопис протягом однієї години, після чого до нього приєднався другий. Через 2 год після початку роботи другого оператора було набрано половину рукопису. За скільки годин може набрати рукопис кожен оператор, працюючи самостійно, якщо другому оператору на це потрібно на 3 год більше, ніж першому?
3.2. Яка ймовірність того, що при одночасному підкиданні трьох монет випаде два орли і одна решка?
3.3. Перпендикуляр, проведений з точки кола до його радіуса, дорівнює 24 см. Цей перпендикуляр ділить радіус у відношенні 5 : 8, починаючи від центра кола. Знайдіть довжину кола.
ВАРІАНТ 19
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Округліть до цілих число: 28,75
А) 28,8 Б) 29 В) 28 Г) 28,7
1.2. Обчисліть значення виразу : (-3,5 + 15) : (-10,8 + 5,8)
А) -3,7 Б) 2,3 В) 3,7 Г) -2,3
1.3. Яка з наведених систем є системою двох лінійних рівнянь з двома змінними?
А) ![]() Б)
Б) 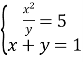 В)
В) ![]() Г)
Г) ![]()
1.4. Знайдіть значення змінної ![]() , при якому вирази
, при якому вирази ![]() рівні.
рівні.
А) ![]() Б)
Б) ![]() В) 5 Г) 7
В) 5 Г) 7
1.5. Розв’яжіть рівняння: ![]()
А) 2 Б) -4 ; 4 В) 4 Г) -4
1.6. Виконайте віднімання: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Знайдіть суму перших восьми членів арифметичної прогресії ![]() , якщо
, якщо ![]()
А) -72 Б) -36 В) 56 Г) 72
1.8. Яка з наведених систем нерівностей не має розв’язку?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. У якій точці розміщено центр кола, вписаного в даний трикутник?
А) у точці перетину медіан трикутника
Б) у точці перетину серединних перпендикулярів до сторін трикутника
В) у точці перетину висот трикутника
Г) у точці перетину бісектрис трикутника
1.10. Знайдіть довжину хорди, що проведена в колі радіуса 15 см на відстані 12 см від центра.
А) 10 см Б) 9 см В) 20 см Г) 18 см
1.11. Укажіть координати вектора ![]() , протилежного до вектора
, протилежного до вектора ![]()
А) (5 ; -7) Б) (-7 ; -5) В) (7 ; -5) Г) (7 ; 5)
1.12. У трикутнику ![]() см. Знайдіть радіус кола, описаного навколо трикутника.
см. Знайдіть радіус кола, описаного навколо трикутника.
А) ![]() см Б)
см Б) ![]() см В)
см В) ![]() см Г)
см Г) ![]() см
см
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз : ![]()
2.2. Звільніться від ірраціональності у знаменнику дробу : ![]()
2.3. Розв’яжіть систему нерівностей : ![]()
2.4. Знайдіть довжину медіани АМ трикутника АВС, якщо А(5 ; -1) , В(-4 ; 3), С(6 ; 1)
Частина третя
3.1. Дві бригади мали разом виготовити 250 деталей. До обіду перша бригада виконала 60 % свого завдання, а друга – 70 % свого. При цьому перша бригада виготовила на 6 деталей менше, ніж друга. Скільки деталей повинна була виготовити кожна бригада?
3.2. Доведіть, що значення виразу ![]()
не залежить від значення змінної.
3.3. У прямокутну трапецію вписано коло, радіус якого дорівнює 6 см. Точка дотику поділяє більшу бічну сторону трапеції на два відрізки, довжина більшого з яких дорівнює 8 см. Знайдіть площу трапеції.
ВАРІАНТ 20
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Знайдіть значення виразу : 789 – (289 – 25)
А) 475 Б) 525 В) 485 Г) 575
1.2. Укажіть усі спільні дільники чисел 12 і 18
А) 1, 2, 4, 6 Б) 2, 4, 6 В) 1, 2, 3, 6 Г) 2, 3
1.3. Розв’яжіть рівняння: ![]()
А) -9,5 Б) 4 В) 9,5 Г) - 4
1.4. Яка з поданих систем рівнянь має безліч розв’язків?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Знайдіть різницю дробів: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. При яких ![]() значення тричлена
значення тричлена ![]() дорівнює нулю?
дорівнює нулю?
А) 2 ; 1 Б) -1 ; 2 В) ![]() Г)
Г) ![]()
1.7. Оцініть значення виразу: ![]() , якщо
, якщо ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Знайдіть порядковий номер члена ![]() арифметичної прогресії, якщо
арифметичної прогресії, якщо ![]()
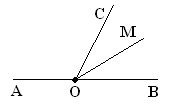 А) 7 Б) 10 В) 8 Г) 9
А) 7 Б) 10 В) 8 Г) 9
1.9. Промінь ОМ – бісектриса ![]() . Знайдіть градусну міру
. Знайдіть градусну міру ![]() , якщо
, якщо ![]() - розгорнутий.
- розгорнутий.
А) 120° Б) 160° В) 30° Г) 150°
1.10. Укажіть правильне твердження:
А) квадрат – це прямокутник, у якого всі сторони рівні;
Б) діагоналі прямокутника, який не є квадратом, перпендикулярні;
В) діагоналі ромба, який не є квадратом, рівні;
Г) сума кутів чотирикутника дорівнює 180°
1.11. Обчисліть ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.12. Знайдіть довжину вектора ![]() , якщо
, якщо ![]()
А) 5 Б) 3 В) ![]() Г)
Г) ![]()
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Графіком квадратичної функції є парабола, що має вершину (0 ; 2) і проходить через точку В(1 ; 6). Задайте цю функцію формулою.
2.3. Не виконуючи побудов, знайдіть точки перетину прямої ![]() і кола
і кола ![]()
2.4. У прямокутнику перпендикуляр, опущений з вершини на діагональ, поділяє її на відрізки 4 см і 9 см. Знайдіть площу прямокутника.
Частина третя
3.1. Добуток цифр двоцифрового натурального числа втричі менший за саме число. Якщо до цього числа додати 18, то отримаємо число, яке записано тими самими цифрами, але у зворотному порядку. Знайдіть це число.
3.2. Побудуйте графік функції 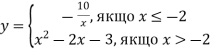 Користуючись побудованим графіком, знайдіть найменше значення цієї функції.
Користуючись побудованим графіком, знайдіть найменше значення цієї функції.
3.3. Знайдіть радіус кола, описаного навколо рівнобічної трапеції, основи якої дорівнюють 11 см і 21 см, а бічна сторона – 13 см.
ВАРІАНТ 21
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Запишіть
 т + 150 кг у кілограмах.
т + 150 кг у кілограмах.
А) 650 кг Б) ![]() кг В) 200 кг Г) 155 кг
кг В) 200 кг Г) 155 кг
1.2. Знайдіть різницю: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.3. Виконайте множення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Яка з точок належить графіку функції: ![]()
А) (2 ; 5) Б) (-1 ; 1) В) (1 ; 1) Г) (1 ; -1)
1.5. Піднесіть до степеня: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Звільніться від ірраціональності в знаменнику дробу: ![]()
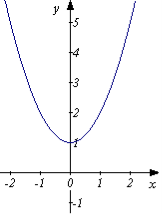 А)
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Графік якої функції зображено на рисунку?
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
1.8. Провівши опитування 10 жінок про розмір їхнього взуття, отримали такі дані: 38 ; 39; 37; 39; 38; 38; 40; 37; 35; 38. Знайдіть моду отриманих даних.
А) 39 Б) 38 В) 40 Г) 37
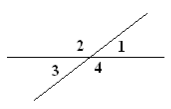 1.9. Якими є кути 1 та 2, зображені на малюнку?
1.9. Якими є кути 1 та 2, зображені на малюнку?
А) вертикальними Б) прямими
В) суміжними Г) тупими
1.10. Знайдіть відрізки, на які ділить середню лінію діагональ трапеції, основи якої дорівнюють 4 см і 10 см.
А) 4 см і 5 см Б) 3 см і 5 см В) 2 см і 4 см Г) 2 см і 5 см
1.11. У рівнобедреному трикутнику бічна сторона дорівнює 8 см, а кут при основі - 30°. Знайдіть площу трикутника.
А) ![]() см2 Б) 16 см2 В)
см2 Б) 16 см2 В) ![]() см2 Г) 32 см2
см2 Г) 32 см2
1.12. Знайдіть відстань від початку координат до середини відрізка АВ, якщо А(3 ; -2) , В(-1 ; 4).
А) ![]() Б)
Б) ![]() В) 2 Г) 13
В) 2 Г) 13
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. При яких значеннях ![]() сума дробів
сума дробів ![]() дорівнює їх добутку?
дорівнює їх добутку?
2.2. Графік функції ![]() паралельний осі абсцис і проходить через точку В(3 ; -2). Знайдіть значення
паралельний осі абсцис і проходить через точку В(3 ; -2). Знайдіть значення ![]() .
.
2.3. Запишіть нескінченні періодичні дроби у вигляді звичайних та обчисліть значення виразу: 0,2(3) – 0,(15) .
2.4. У прямокутній трапеції більша діагональ дорівнює 15 см, висота – 12 см, а менша основа – 4 см. Знайдіть більшу бічну сторону трапеції.
Частина третя
3.1. Катер проплив 40 км за течією річки і 16 км проти течії, витративши на весь шлях 3 год. Якою є власна швидкість катера, якщо швидкість течії 2 км/год?
3.2. Відомо, що для будь-якого натурального n сума Sn перших n членів деякої арифметичної прогресії виражається формулою ![]() . Знайдіть перший член прогресії та її різницю.
. Знайдіть перший член прогресії та її різницю.
3.3. Центр кола, описаного навколо трапеції, належить більшій основі. Знайдіть кути трапеції, якщо основи відносяться як 1 : 2.
ВАРІАНТ 22
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Знайдіть корінь рівняння:
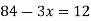
А) 216 Б) 32 В) 288 Г) 24
1.2. Виконайте ділення: ![]()
А) 8 Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.3. Запишіть вираз: ![]() у вигляді квадрата двочлена:
у вигляді квадрата двочлена:
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Спростіть вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Яке з чисел подано в стандартному вигляді?
А) 1,24 ∙ 10 -7 Б) 1,7 ∙ 510 В) 53,7012 Г) 18,25 ∙ 1010
1.6. Піднесіть до степеня: 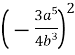
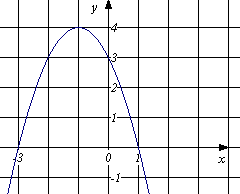 А)
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. На рисунку зображено графік функції ![]() . Знайдіть множину розв’язків нерівності:
. Знайдіть множину розв’язків нерівності: ![]() .
.
А) (-3 ; 1) Б) ![]()
В) ![]() Г) [-3 ; 1]
Г) [-3 ; 1]
1.8. При якому значенні ![]() функція
функція ![]() набуває найменшого значення?
набуває найменшого значення?
А) 3 Б) 5 В) -5 Г) -3
1.9. Один із кутів, що утворився при перетині двох паралельних прямих січною, дорівнює 25°. Яким може бути один з решти семи кутів?
А) 155° Б) 145° В) 165° Г) 90°
1.10. Відрізки ![]() перетинаються в точці О. Відомо, що
перетинаються в точці О. Відомо, що ![]()
![]() Знайдіть
Знайдіть ![]() , якщо
, якщо ![]() .
.
А) 55° Б) 40° В) 45° Г) 50°
1.11. Центральний кут правильного многокутника дорівнює 30°. Визначте кількість сторін многокутника.
А) 6 сторін Б) 10 сторін В) 12 сторін Г) 18 сторін
1.12. Знайдіть бічну сторону рівнобедреного трикутника, якщо кут при вершині дорівнює 30°, а його площа – 24 см2 .
А) ![]() см Б)
см Б) ![]() см В)
см В) ![]() см Г)
см Г) ![]() см
см
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть значення виразу: ![]() , якщо
, якщо ![]()
2.2. Корені ![]() рівняння
рівняння ![]() задовольняють умову
задовольняють умову ![]() . Знайдіть
. Знайдіть ![]() .
.
2.3. Одночасно підкинули два гральних кубики. Знайдіть ймовірність того, що сума очок на кубиках дорівнює 9.
2.4. Знайдіть кут між меншою стороною і діагоналлю прямокутника, якщо він на 70° менший від кута між діагоналями, який лежить проти більшої сторони.
Частина третя
3.1. З міста в село, відстань між якими 450 км, виїхали одночасно два автомобілі. Швидкість одного з них була на 10 км/год більша, ніж швидкість іншого, і тому він прибув у село на 30 хв швидше. Знайдіть швидкість кожного автомобіля.
3.2. Побудуйте графік функції 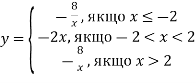
Користуючись побудованим графіком, знайдіть проміжки зростання функції та її найбільше значення.
3.3. Коло, вписане у прямокутну трапецію, ділить точкою дотику більшу бічну сторону на відрізки завдовжки 4 см і 25 см. Знайдіть площу трапеції.
ВАРІАНТ 23
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
При якому із запропонованих значень
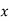 дріб
дріб  правильний?
правильний?
А) 5 Б) 7 В) 1 Г) 10
1.2. Довжина автомобільної траси 180 км. Знайдіть довжину цієї траси на карті з масштабом 1 : 5 000 000.
 А) 3,6 см Б) 90 см В) 36 см Г) 9 см
А) 3,6 см Б) 90 см В) 36 см Г) 9 см
1.3. Користуючись графіком, знайдіть значення аргументу, якщо значення функції дорівнює -1.
А) -1; 1 Б) 1 В) 0 Г) -3; 3
1.4. Розкладіть многочлен ![]() на множники.
на множники.
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
1.5. Спростіть вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Подайте число 0,0000125 у стандартному вигляді.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. У ящику є 20 пронумерованих від 1 до 20 жетонів. Яка ймовірність того, що навмання взятий з ящика жетон буде з числом, кратним 6?
А) 1 Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Яка з нерівностей є правильною за будь-якого значення ![]() ?
?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. Відомо, що ![]() . Знайдіть градусну міру
. Знайдіть градусну міру ![]()
А) 46° Б) 80° В) 54° Г) 100°
1.10. Знайдіть кути прямокутного трикутника, якщо синус одного з гострих кутів дорівнює ![]()
А) 90° ; 30° ; 60° Б) 90° ; 45° ; 30° В) 90° ; 60; 45° Г) 90° ; 45°; 45°
1.11. Знайдіть відстань між точками А(6 ; -3) і В(2 ; -1)
А) 20 Б) 80 В) ![]() Г)
Г) ![]()
1.12. Площа круга, вписаного в квадрат, дорівнює 4π см2. Знайдіть сторону квадрата.
А) ![]() см Б) 4 см В) 2 см Г)
см Б) 4 см В) 2 см Г) ![]() см
см
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Знайдіть найбільше ціле число, яке є розв’язком системи нерівностей: ![]()
2.3. Побудуйте графік функції ![]() . У банк відповідей запишіть найменше значення функції.
. У банк відповідей запишіть найменше значення функції.
2.4. Висота, проведена з вершини тупого кута рівнобічної трапеції, ділить її основу на відрізки 4 см і 6 см. Знайдіть середню лінію трапеції.
Частина третя
3.1. Автомобіль мав проїхати 1200 км з певною швидкістю. Після того як він проїхав третину шляху із цією швидкістю, автомобіль витратив на зупинку 2 год. Збільшивши швидкість на 20 км/год, автомобіль прибув у пункт призначення вчасно. Якою була швидкість автомобіля спочатку?
3.2. Доведіть, що значення виразу ![]()
є додатним при всіх допустимих значеннях змінної.
3.3. Бісектриса гострого кута паралелограма ділить його сторону у відношенні 3 : 4, рахуючи від вершини тупого кута. Периметр паралелограма дорівнює 80 см. Знайдіть його сторони.
ВАРІАНТ 24
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Обчисліть:
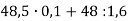
А) 34,85 Б) 515 В) 351,875 Г) 7,85
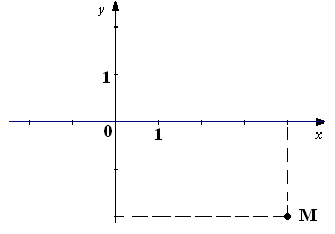 1.2. Користуючись рисунком, запишіть координати точки М.
1.2. Користуючись рисунком, запишіть координати точки М.
А) (4 ; 2) Б) (-2 ; 4)
В) (4 ; -2) Г) (-4 ;-2)
1.3. Укажіть пару чисел, яка є розв’язком рівняння: ![]()
А) (1 ; 6) Б) (6 ; 1)
В) (-1 ; -6) Г) (6 ; -1)
1.4. Яке з рівнянь рівносильне рівнянню: ![]() ?
?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Укажіть більший корінь рівняння: ![]()
А) -5 Б) 5 В) 1 Г) -1
1.6. Скоротіть дріб: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Знайдіть суму перших п’яти членів геометричної прогресії ![]() , якщо
, якщо ![]()
А) 33 Б) 31 В) -31 Г) 11
1.8. Укажіть усі значення змінної ![]() , при яких вираз
, при яких вираз ![]() має зміст
має зміст
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. Яке взаємне розміщення двох кіл з радіусами 5 см і 10 см, якщо відстань між їх центрами дорівнює 20 см?
А) перетинаються у двох точках;
Б) не мають спільних точок;
В) збігаються ;
Г) дотикаються.
1.10. З точки М до прямої ![]() проведено перпендикуляр MN i похилу МК. Знайдіть довжину проекції NK, якщо MN = 12 см, МК = 13 см.
проведено перпендикуляр MN i похилу МК. Знайдіть довжину проекції NK, якщо MN = 12 см, МК = 13 см.
А) 6 см Б) 1 см В) 25 см Г) 5 см
1.11. Обчисліть скалярний добуток векторів: ![]() .
.
А) ![]() Б) 38 В) 2 Г) -2
Б) 38 В) 2 Г) -2
1.12. У трикутнику АВС знайдіть кут В, якщо ![]() .
.
А) 135° Б) 75° В) 65° Г) 45°
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть: ![]()
2.2. Спростіть вираз: 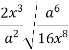 , якщо
, якщо ![]()
2.3. Знайдіть область визначення функції 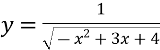
2.4. Пряма, яка паралельна стороні АВ трикутника АВС, перетинає сторони СА і СВ цього трикутника у точках М і N відповідно. АВ = 15 см, MN = 6 см, АМ = 3 см. Знайдіть довжину сторони АС.
Частина третя
3.1. Знаменник звичайного нескоротного дробу на 3 більший від чисельника. Якщо чисельник цього дробу збільшити на 2, а знаменник – на 10, то дріб зменшиться на ![]() . Знайдіть цей дріб.
. Знайдіть цей дріб.
3.2. Побудуйте графік функції ![]() .
.
3.3. Периметр паралелограма дорівнює 26 см, а його діагоналі дорівнюють 7 см і 11 см. Знайдіть сторони паралелограма.
ВАРІАНТ 25
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Знайдіть значення виразу: 56 + 42 : 14 – 7
А) 52 Б) 50 В) 49 Г) 0
1.2. Чому дорівнює найменше спільне кратне чисел: 12 і 16?
А) 2 Б) 4 В) 48 Г) 96
1.3. Яке з рівнянь є лінійним?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Яка пара чисел є розв’язком системи: ![]() ?
?
А) (-1 ; -2) Б) (2 ; 1) В) (1 ; 2) Г) (-1 ; 2)
1.5. Скоротіть дріб: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Чому дорівнює сума коренів квадратного рівняння: ![]() ?
?
А) 5 Б) 9 В) -5 Г) -9
1.7. Відомо, що ![]() . Яка з нерівностей хибна?
. Яка з нерівностей хибна?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Знайдіть суму нескінченої геометричної прогресії: -6 ; 1 ; ![]() …
…
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
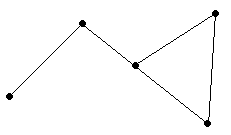 1.9. Скільки відрізків зображено на рисунку?
1.9. Скільки відрізків зображено на рисунку?
А) 4 Б) 5 В) 6 Г) 7
1.10. У прямокутнику ![]()
![]() - точка перетину діагоналей,
- точка перетину діагоналей, ![]() . Знайдіть
. Знайдіть ![]() .
.
А) 45° Б) 25° В) 50° Г) 130°
1.11. Знайдіть сторону АС трикутника АВС, якщо ![]() .
.
А) ![]() см Б) 19 см В) 49 см Г) 7 см
см Б) 19 см В) 49 см Г) 7 см
1.12. При якому значенні ![]() скалярний добуток векторів
скалярний добуток векторів ![]() дорівнює 10?
дорівнює 10?
А) 0 Б) 10 В) -5 Г) 5
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть значення виразу: ![]()
2.2. Знайдіть точки параболи, що є графіком функції ![]() , у яких абсциса й ордината – протилежні числа.
, у яких абсциса й ордината – протилежні числа.
2.3. Розв’яжіть систему рівнянь: 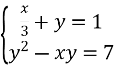
2.4. Хорда, довжина якої ![]() см, стягує дугу кола, градусна міра якої 90°. Знайдіть довжину кола.
см, стягує дугу кола, градусна міра якої 90°. Знайдіть довжину кола.
Частина третя
3.1. Скільки грамів 3-відсоткового і скільки грамів 8-відсоткового розчинів солі треба взяти, щоб отримати 260 г 5-відсоткового розчину солі?
3.2. Розв’яжіть рівняння ![]() .
.
3.3. Кола, радіуси яких дорівнюють 4 см і 9 см, мають зовнішній дотик. До кіл проведено спільну зовнішню дотичну. Знайдіть відстань між точками дотику.
ВАРІАНТ 26
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Знайдіть різницю: 16 год 26 хв – 9 год 52 хв
А) 7 год 26 хв Б) 7 год 34 хв В) 6 год 34 хв Г) 6 год 26 хв
1.2. Знайдіть суму: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.3. Який з виразів є одночленом?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Областю визначення якої з функцій є будь-які значення ![]() ?
?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Виконайте ділення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Обчисліть значення виразу: ![]()
А) ![]() Б) 8 В) 2 Г)
Б) 8 В) 2 Г) ![]()
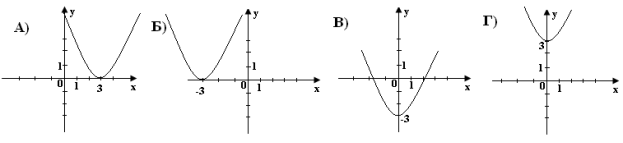 1.7. На якому з графіків зображено графік функції
1.7. На якому з графіків зображено графік функції ![]()
1.8. Яка ймовірність того, що при одному підкиданні грального кубика випаде кількість очок, що дорівнює парному числу?
А) 1 Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. Бісектриса кута А утворює з його стороною кут 25°. Знайдіть градусну міру кута, суміжного з кутом А.
А) 75° Б) 25° В) 50° Г) 130°
1.10. Кути рівнобічної трапеції можуть дорівнювати…
А) 40° і 50° Б) 120° і 150° В) 70° і 110° Г) 155° і 35°
1.11. Знайдіть площу трикутника АВС, якщо АВ = 3 см, ВС = 6 см, ![]() °.
°.
А) 9 см2 Б) ![]() см2 В)
см2 В) ![]() см2 Г)
см2 Г) ![]() см2
см2
1.12. Складіть рівняння кола з центром у точці М( -3 ; 1), яке проходить через точку К( -1 ; 5) .
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. На прямій ![]() знайдіть точку, абсциса якої удвічі більша за ординату.
знайдіть точку, абсциса якої удвічі більша за ординату.
2.3. Знайдіть суму двадцяти перших членів арифметичної прогресії ![]() , якщо
, якщо ![]() ,
, ![]()
2.4. Дві сторони трикутника дорівнюють ![]() см і 10 см, а кут проти більшої з них 45°. Знайдіть третю сторону трикутника.
см і 10 см, а кут проти більшої з них 45°. Знайдіть третю сторону трикутника.
Частина третя
3.1. З міста A в місто B виїхав велосипедист. Через 3 год у тому самому напрямі з міста A виїхав мотоцикліст і прибув у місто B одночасно з велосипедистом. Знайдіть швидкість велосипедиста, якщо вона менша за швидкість мотоцикліста на 45 км/год, а відстань між містами дорівнює 60 км.
3.2. Побудуйте графік функції ![]() .
.
3.3. У трикутнику одна зі сторін дорівнює 29 см, а інша ділиться точкою дотику вписаного в нього кола на відрізки завдовжки 24 см і 1 см, починаючи від кінця першої сторони. Знайдіть площу трикутника.
ВАРІАНТ 27
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Яке з чисел 3 ; 12 ; 14 є коренем рівняння:
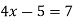 ?
?
А) 12 Б) жодного В) 3 Г) 14
1.2. Виконайте множення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.3. Подайте у вигляді многочлена вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Спростіть вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Обчисліть значення виразу: ![]()
А) 14 Б) 6 В) 40 Г) 636
1.6. Виконайте ділення: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Для якої нерівності число 1 є розв’язком?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Вершина якої з парабол належить осі абсцис?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
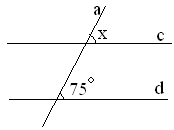 1.9. Якої градусної міри має бути кут
1.9. Якої градусної міри має бути кут ![]() , щоб прямі
, щоб прямі ![]() були паралельні (див. рис.)?
були паралельні (див. рис.)?
А) 150° Б) 105° В) 75° Г) 15°
1.10. Прямі MN і РК паралельні. Відрізки PN і КМ перетинаються в точці О, при цьому MN = 4 см, РК = 6 см. Знайдіть відношення NO : OP.
А) 1 : 3 Б) 3 : 2 В) 2 : 3 Г) 1 : 2
1.11. Знайдіть довжину дуги кола, градусна міра якої дорівнює 60°, якщо радіус кола 3 см.
А) π см Б) ![]() см В)
см В) ![]() см Г) 2π см
см Г) 2π см
1.12. Площа трикутника АВС дорівнює ![]() см2 . Знайдіть кут В трикутника, якщо АВ = 8 см , ВС = 10 см.
см2 . Знайдіть кут В трикутника, якщо АВ = 8 см , ВС = 10 см.
А) 45° Б) 90° В) 60° Г) 30°
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: ![]()
2.2. Один з коренів рівняння ![]() дорівнює 1,5 . Знайдіть
дорівнює 1,5 . Знайдіть ![]() і другий корінь рівняння.
і другий корінь рівняння.
2.3. У сплаві 60% міді, а решта – 200г – олово. Яка маса сплаву?
2.4. У ![]() . Знайдіть довжину гіпотенузи трикутника.
. Знайдіть довжину гіпотенузи трикутника.
Частина третя
3.1. Два автомобілі одночасно виїхали з одного міста в інше. Швидкість першого на 10 км/год більша за швидкість другого, і тому він витратив на весь шлях на 1 годину менше, ніж другий. Знайдіть швидкість кожного автомобіля, якщо відстань між містами 560 км.
3.2. Знайдіть область допустимих значень функції ![]()
3.3. Медіани прямокутного трикутника, проведені до катетів, дорівнюють 3 см і 4 см. Знайдіть гіпотенузу трикутника.
ВАРІАНТ 28
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Виконайте додавання:
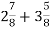
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.2. Знайдіть відсоткове відношення 0,2 до ![]()
А) 16% Б) 62,5% В) 1,6% Г) 6,25%
1.3. Укажіть функцію, яка є прямою пропорційністю
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. Спростіть вираз: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.5. Серед наведених чисел укажіть ірраціональне число
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Знайдіть значення виразу: ![]()
А) 10,25 Б) 6 В) 14 Г) 5
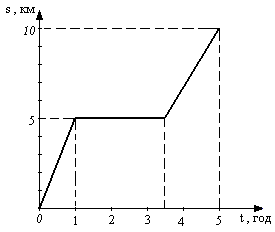 1.7. На рисунку зображено графік руху туриста. Скільки часу тривав привал?
1.7. На рисунку зображено графік руху туриста. Скільки часу тривав привал?
А) 1 год
Б) 5 год
В) 3,5 год
Г) 2,5 год
1.8. Розв’яжіть нерівність: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. Знайдіть кут при вершині рівнобедреного трикутника, якщо кут при основі дорівнює 30°.
А) 40° Б) 90° В) 120° Г) 60°
1.10. Катети прямокутного трикутника дорівнюють 6 см і 8 см. Знайдіть тангенс кута, протилежного до більшого з катетів.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.11. Знайдіть відстань від точки А( -8 ; 6) до початку координат.
А) 9 Б) 10 В) ![]() Г)
Г) ![]()
1.12. Навколо рівностороннього трикутника описано коло радіуса 4 см. Знайдіть площу трикутника.
А) ![]() см2 Б)
см2 Б) ![]() см2 В)
см2 В) ![]() см2 Г) 12 см2
см2 Г) 12 см2
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Спростіть вираз: 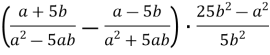
2.2. Знайдіть натуральні розв’язки нерівності: ![]()
2.3. Побудуйте графік функції: ![]() . У бланк відповідей запишіть область значень цієї функції.
. У бланк відповідей запишіть область значень цієї функції.
2.4. Дано вектори: ![]() . Знайдіть кут між векторами
. Знайдіть кут між векторами ![]() .
.
Частина третя
3.1. Дано двоцифрове натуральне число, сума квадратів цифр якого дорівнює 45. Якщо до цього числа додати 27, то отримаємо число, що записане тими самими цифрами, але у зворотному порядку. Знайдіть дане число.
3.2. Розв’яжіть рівняння ![]() .
.
3.3. Катети прямокутного трикутника відносяться як 20 : 21, а різниця між радіусами описаного та вписаного кіл дорівнює 17 см. Знайдіть гіпотенузу трикутника.
ВАРІАНТ 29
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
- Запишіть десятковий дріб 3,07 у вигляді мішаного числа
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.2. Обчисліть значення виразу: ![]()
А) -12,15 Б) 3,15 В) -3,15 Г) -1,35
1.3. Укажіть пару чисел, яка є розв’язком рівняння: ![]()
А) (-2 ; 3) Б) (-2 ; -3) В) (-3 ; 2) Г) (2 ; 3)
1.4. Знайдіть значення змінної ![]() , при якому значення виразів
, при якому значення виразів ![]() рівні
рівні
А) ![]() Б)
Б) ![]() В) 4 Г) -4
В) 4 Г) -4
1.5. Знайдіть корені квадратного рівняння: ![]()
А) 1 і 7 Б) -7 і -1 В) -7 і 1 Г) -1 і 7
1.6. Виконайте додавання: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.7. Знайдіть різницю арифметичної прогресії: 8; 3; -2; -7 …
А) 8 Б) 3 В) 5 Г) -5
1.8. Розв’яжіть систему нерівностей: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.9. Скільки спільних точок має пряма з колом, діаметр якого дорівнює 8 см, якщо пряма розміщена на відстані 4 см від центра кола?
А) три Б) жодної В) дві Г) одну
1.10. У прямокутному рівнобедреному трикутнику гіпотенуза дорівнює ![]() см. Знайдіть катет.
см. Знайдіть катет.
А) 4 см Б) ![]() см В)
см В) ![]() см Г) 2 см
см Г) 2 см
1.11. Знайдіть координати вектора ![]() , якщо А( -3 ; 2) , В( -1 ; -2)
, якщо А( -3 ; 2) , В( -1 ; -2)
А) ( 2 ; - 4) Б) ( 4 ; 0) В) ( – 2 ; 4) Г) ( - 4 ; 0)
1.12. У трикутнику АВС сторона АВ = 5 см, ВС = 3 см, ![]() . Знайдіть сторону АС.
. Знайдіть сторону АС.
А) 49 см Б) 19 см В) 7 см Г) ![]() см
см
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Обчисліть: ![]()
2.2. Скоротіть дріб: ![]()
2.3. Знайдіть усі цілі розв’язки нерівності: ![]()
2.4. Знайдіть на осі абсцис точку, рівновіддалену від точок А(1 ; 5) і В(3 ; 1)
Частина третя
3.1. Знайдіть чотири послідовних непарних натуральних числа, якщо добуток другого і третього на 111 більший, ніж потроєна сума першого і четвертого.
3.2. Розв’яжіть систему рівнянь 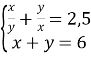
3.3. Точка перетину бісектрис гострих кутів при більшій основі трапеції належить меншій основі. Знайдіть площу трапеції, якщо її бічні сторони дорівнюють 17 см і 25 см, а висота – 15 см.
ВАРІАНТ 30
Частина перша
Завдання 1.1 – 1.12 мають по чотири варіанти відповідей, з яких тільки ОДНА відповідь ПРАВИЛЬНА. Оберіть правильну, на вашу думку, відповідь і позначте її у бланку відповідей.
-
Знайдіть значення виразу:
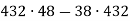
А) 4320 Б) 8 941 536 В) 3420 Г) 37 152
1.2. Яке число є дільником числа 12?
А) 6 Б) 7 В) 24 Г) 48
1.3. Яке з рівнянь не має коренів?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.4. На якому з рисунків зображено графік рівняння: ![]() ?
?
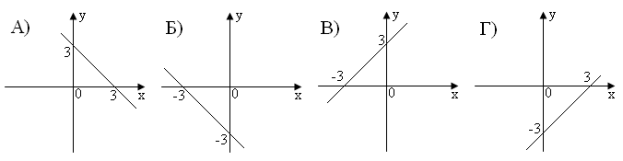
1.5. Виконайте додавання: ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.6. Скільки коренів має рівняння: ![]() ?
?
А) безліч Б) жодного В) один Г) два
1.7. Оцініть значення виразу: ![]() , якщо
, якщо ![]()
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.8. Знайдіть перший член арифметичної прогресії ![]() , якщо
, якщо ![]()
А) 5 Б) 15 В) 10 Г) 11
1.9. На якій відстані від кінців відрізка завдовжки 70 см лежить точка, яка поділяє його на дві частини у відношенні 5 : 2?
А) 14 см, 56 см Б) 56 см, 14 см В) 50 см, 70 см Г) 50 см, 20 см
1.10. У ромбі ABCD кут ABD дорівнює 75°. Чому дорівнює кут АВС?
А) 140° Б) 150° В) 75° Г) 30°
1.11. У трикутнику ![]() . Знайдіть сторону
. Знайдіть сторону ![]() .
.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
1.12. Який з векторів колінеарний вектору ![]() ?
?
А) (3 ; 4) Б) (6 ; 9) В) ( 9 ; 6) Г) (1 ; 2)
Частина друга
Розв’яжіть завдання 2.1 – 2.4. Запишіть відповідь у бланк відповідей.
2.1. Розв’яжіть рівняння: ![]()
2.2. Графіку функції ![]() належить точка А( -2 ; 9). Знайдіть коефіцієнт
належить точка А( -2 ; 9). Знайдіть коефіцієнт ![]()
2.3. Розв’яжіть систему рівнянь: 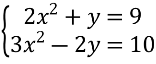
2.4. У рівнобедреному трикутнику висота, проведена до бічної сторони, поділяє її на відрізки 8 см і 5 см, рахуючи від вершини кута при основі. Знайдіть площу трикутника.
Частина третя
3.1. Дві бригади, працюючи разом, зорали поле за 6 днів. За скільки днів може зорати поле кожна бригада, працюючи самостійно, якщо другій бригаді на це потрібно на 5 днів менше, ніж першій?
3.2. Розв’яжіть рівняння ![]()
3.3. Знайдіть площу паралелограма, діагоналі якого дорівнюють 8 см і 10 см, а одна з діагоналей перпендикулярна до сторони.
1


про публікацію авторської розробки
Додати розробку

-

Ткаченко Людмила
16.05.2024 в 17:36
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вращук Ірина
20.10.2023 в 23:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Федорівна Тетяна
04.10.2023 в 16:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Малик Наталія
10.05.2023 в 16:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

vlad vladimer
05.02.2023 в 14:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мащакевич Ліана Анатоліївна
08.05.2022 в 21:18
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пасічняк Олександра
04.04.2022 в 11:55
Дуже дякую
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Хомко Людмила Михайлівна
21.07.2021 в 16:22
дуже дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Шеїн Марина Миколаївна
17.05.2021 в 19:05
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Temnyk Mariya
24.03.2020 в 10:40
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Morgulets Oksana
09.02.2020 в 21:14
Корисний матеріал. Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лагановська Світлана
03.02.2020 в 12:29
дякую
Загальна:
4.3
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Доліч Наталія
02.01.2020 в 20:12
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 10 відгуків