збірник завдань до проекту 10 клас алгебра "Тригонометричні рівняння та нерівності"
Назва проекту:
«Тригонометричні рівняння та нерівності»
10 клас алгебра
Збірник
«Різні види тригонометричних рівнянь
і нерівностей та методи їх розв'язування»
Керівник проекту: вчитель математики Мохова Ольга Петрівна
Зміст.
1. Зведення до однієї функції одного виду
2. Зведення до однієї функції другого виду
3. Однорідні рівняння відносно Sinx та Cosx.
4. Рівняння, які приводять до однорідних.
5. Використання формули ![]()
6. Заміна ![]()
7. Розкладання на множники
8. Зниження степеня
9. Порівняння лівої та правої частини
Основні прийоми рішення тригонометричних
рівнянь та нерівностей.
Деякі тригонометричні рівняння можна привести шляхом тотожних перетворень до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебраїчного.
1. Зведення до однієї функції
![]() заміняємо на
заміняємо на ![]() ,
, ![]() – на
– на ![]() .
.
Приклад 1.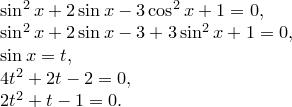
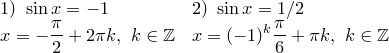
Приклад 2.![\begin{array}{l}<br />
{\rm ctg}\, x-3{\rm tg}\, x=0,\\<br />
\displaystyle<br />
{1\over {\rm tg}\, x}-3{\rm tg}\, x=0,\\[3mm]<br />
1-3{\rm tg}^2x=0\\<br />
\displaystyle<br />
{\rm tg}^2x={1\over 3}\quad(\Longrightarrow\cos x\ne0,\sin x\ne0),\\[3mm]<br />
\displaystyle<br />
{\rm tg}\, x=\pm{1\over\sqrt{3}},\\[2mm]<br />
\displaystyle<br />
x=\pm{\pi\over 6}+\pi k.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.009.png)
2. ![]() заміняємо на
заміняємо на ![]() ,
, ![]() – на
– на ![]() ,
, ![]() – на
– на ![]() .
.
Приклад 1.
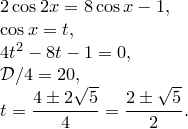
1) ![]() 2)
2) ![]() ,
,
В першому випадку рішення немає, в другому ![]() .
.
Приклад 2.
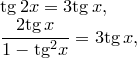
![\begin{array}{ll}<br />
1)\ {\rm tg}\, x=0&2)\ {\rm tg}\, x\ne0,\\<br />
x=\pi k,\ k\in\mathbb{Z}&\displaystyle {2\over 1-{\rm tg}^2x}=3,\\[3mm]<br />
&3{\rm tg}^2x-1=0,\\<br />
&{\rm tg}^2x=1/3\Rightarrow\cos x\ne0,\ {\rm tg}^2x\ne1,\\<br />
&\displaystyle {\rm tg}\, x=\pm{\sqrt{3}\over 3},\\[3mm]<br />
&\displaystyle x=\pm{\pi\over 6}+\pi k,\ k\in\mathbb{Z}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.019.png)
Приклад 3.
![\begin{array}{ll}<br />
{\rm tg}\,2x=3{\rm ctg}\, x&\\<br />
1)\ \displaystyle {2{\rm tg}\, x\over 1-{\rm tg}^2x}={3\over {\rm tg}\, x}\ (\cos x\ne0)&\displaystyle \cos x=0\Longleftrightarrow x={\pi\over 2}+\pi k,\ k\in\mathbb{Z},\\[3mm]<br />
2{\rm tg}^2x=3-3{\rm tg}^2x&\Longrightarrow{\rm tg}\,2x={\rm tg}\,(\pi+2\pi k)=0,\\<br />
5{\rm tg}^2x=3&{\rm ctg}\, x=0,\\<br />
\displaystyle{\rm tg}\, x=\pm\sqrt{3\over 5}\Longrightarrow\cos x\ne0,{\rm tg}^2x\ne1&\\<br />
\displaystyle x=\pm{\rm arctg}\,\sqrt{3\over 5}+\pi k,\ k\in\mathbb{Z}.&<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.020.png)
3. Однорідні рівняння відносно ![]() .
.
![]()
Якщо ![]() , то поділивши обидві частини рівняння на
, то поділивши обидві частини рівняння на ![]() или на
или на ![]() , отримаємо рівносильні рівняння. Дійсно, нехай
, отримаємо рівносильні рівняння. Дійсно, нехай ![]() — корінь рівняння і
— корінь рівняння і ![]() . При підстановці у рівняння, отримаємо що і
. При підстановці у рівняння, отримаємо що і ![]() , а це неможливо.
, а це неможливо.
Приклад.
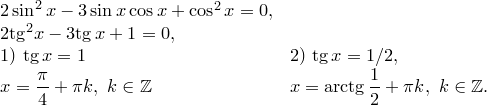
4. Рівняння, які приводять до однорідних.
а) Множення на ![]()
Пример.
б) Перехід до половинного аргументу
Приклад.![\begin{array}{l}<br />
11\sin x-2\cos x=10,\\<br />
\displaystyle<br />
22\sin{x\over 2}\cos{x\over 2}-2\cos^2{x\over 2}+2\sin^2{x\over 2}=10\sin^2{x\over 2}+10\cos^2{x\over 2},\\[3mm]<br />
\displaystyle<br />
4{\rm tg}^2{x\over 2}-11{\rm tg}\,{x\over 2}+6=0,\\[5mm]<br />
\displaystyle<br />
{\rm tg}\,{x\over 2}={11\pm\sqrt{121-96}\over 8}={11\pm5\over 8}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.030.png)
![\begin{array}{ll}<br />
\displaystyle<br />
\displaystyle{\rm tg}\,{x\over 2}=2&\displaystyle{\rm tg}\,{x\over 2}={3\over 4},\\[3mm]<br />
x=2{\rm arctg}\,2+2\pi k,\ k\in\mathbb{Z}&\displaystyle x={\rm arctg}\,{3\over 4}+2\pi k,\ k\in\mathbb{Z}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.031.png)
5. Використання формули
![]()
Приклад.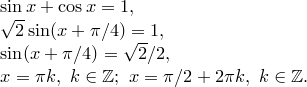
6. Заміна ![]() .
.
Приклад.![\begin{array}{l}<br />
\displaystyle{1\over \sin x}-{1\over \cos x}=1,\\[3mm]<br />
\cos x-\sin x=\sin x\cos x,\\<br />
\cos x-\sin x=t,\\<br />
\displaystyle \sin x\cos x={1-t^2\over 2},\\[3mm]<br />
1-t^2=2t,\\<br />
t^2+2t-1=0,\\<br />
t=-1\pm\sqrt{2}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.033.png)
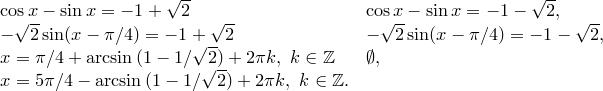
7. Розкладання на множники
1. Формули перетворення суми в добуток
Формулы
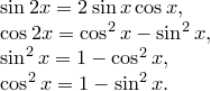
Приклад 1.
![\begin{array}{ll}<br />
\cos2x=\cos x+\sin x,&\\<br />
1)\ \cos x+\sin x=0,&2)\ \cos x-\sin x=1,\\<br />
1+{\rm tg}\, x=0,&-\sqrt{2}\sin(x+{\rm arctg}\,(-1))=1,\\<br />
{\rm tg}\, x=-1,&\displaystyle\sin\left( x-\pi/4\right)=-{\sqrt{2}\over 2},\\[3mm]<br />
\displaystyle x={3\pi\over 4}+\pi k,\ k\in\mathbb{Z}&\displaystyle x-{\pi\over 4}=-{\pi\over 4}+2\pi k,\ x=2\pi k,\ k\in\mathbb{Z},\\[3mm]<br />
&\displaystyle x-{\pi\over 4}={5\pi\over 4}+2\pi k,\ x={3\pi\over 2}+2\pi k,\ k\in\mathbb{Z}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.036.png)
Відповідь. ![]() .
.
Приклад 2.
![\begin{array}{l}</p>
<p>\sin x+\sin^2x+\cos^3x=0,\\<br />
\sin x+1-\cos^2x+\cos^3x=0,\\<br />
\sin x(1+\sin x)+(1-\sin^2x)\cos x=0,\\<br />
\sin x(1+\sin x)+(1+\sin x)(1-\sin x)\cos x=0,\\<br />
1)\ 1+\sin x=0,\\<br />
\sin x=-1,\\<br />
\displaystyle x=-{\pi\over 2}+2\pi k,\ k\in\mathbb{Z},\\<br />
2)\ \sin x+(1-\sin x)\cos x=0,\\<br />
\sin x+\cos x=t,\\<br />
\displaystyle\sin x\cos x={1\over 2}(t^2-1),\\[3mm]<br />
\displaystyle t-{1\over 2}t^2+{1\over 2}=0,\\[3mm]<br />
\displaystyle {1\over 2}t^2-t+{1\over 2}=0,\\[3mm]<br />
t=1\pm\sqrt{2}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.038.png)
![]() , рішення немає,
, рішення немає,
![\begin{array}{l}</p>
<p>2)\ \sin x+\cos x=1-\sqrt{2},\\<br />
\sqrt{2}\sin(x+\pi/4)=1-\sqrt{2},\\<br />
\displaystyle x+{\pi\over 4}=\arcsin{1-\sqrt{2}\over \sqrt{2}}+2\pi k,\ k\in\mathbb{Z},\\[3mm]<br />
\displaystyle x=-{\pi\over 4}+\arcsin{1-\sqrt{2}\over \sqrt{2}}+2\pi k,\ k\in\mathbb{Z},\\[3mm]<br />
\displaystyle x+{\pi\over 4}=\pi-\arcsin{1-\sqrt{2}\over \sqrt{2}}+2\pi k,\ k\in\mathbb{Z},\\[3mm]<br />
\displaystyle x={3\pi\over 4}-\arcsin{1-\sqrt{2}\over \sqrt{2}}+2\pi k,\ k\in\mathbb{Z}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.040.png)
Відповідь. 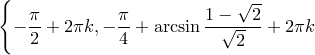 ,
, 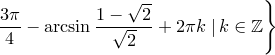 .
.
8. Зниження степеня
Формули
![\begin{array}{l}</p>
<p>\displaystyle<br />
\cos\alpha\cos\beta={1\over 2}(\cos(\alpha+\beta)+\cos(\alpha-\beta)),\\[3mm]<br />
\displaystyle<br />
\sin\alpha\sin\beta={1\over 2}(\cos(\alpha-\beta)-\cos(\alpha+\beta)),\\[3mm]<br />
\displaystyle<br />
\sin\alpha\cos\beta={1\over 2}(\sin(\alpha-\beta)+\sin(\alpha+\beta)),\\[3mm]<br />
\displaystyle<br />
\cos^2\alpha={1\over 2}(1+\cos2\alpha),\\[3mm]<br />
\displaystyle<br />
\sin^2\alpha={1\over 2}(1-\cos2\alpha).<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.043.png)
9. Порівняння лівої та правої частини
Приклад 1.
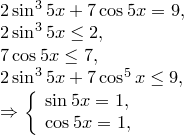
А це неможливо. Відповідь: немає рішення
Приклад 2.
![\begin{array}{l}<br />
\displaystyle\sin^{19}x+\cos^{19}x={\pi\over 3},\\[3mm]<br />
\sin^2x+\cos^2x=1,\\<br />
\left.\begin{array}{l}<br />
\sin^{19}x\le\sin^2x,\\<br />
\cos^{19}x\le\cos^2x,<br />
\end{array}\right|\Rightarrow\sin^{19}x+\cos^{19}x\le1,\\<br />
\pi/3>1.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.045.png)
Відповідь: немає рішення
Приклад 3.
![\begin{array}{l}<br />
\sin3x+\sin7x=2,\\<br />
\left\{\begin{array}{l}<br />
\sin3x=1,\\<br />
\sin7x=1,<br />
\end{array}\right.\\[5mm]<br />
\sin3x=1,\\<br />
\displaystyle x={\pi\over 6}+{2\pi k\over 3},\ k\in\mathbb{Z}.<br />
\end{array}](/uploads/files/42212/184968/200425_html/images/184968.046.png)
нехай![]()
Підставимо значення в друге рівняння:
![]()
Відповідь. ![]() .
.
Приклад 4.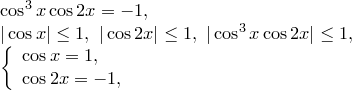
або
![]()
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
![]()
Відповідь. ![]() .
.


про публікацію авторської розробки
Додати розробку
