Конспект уроку математики з використанням навчально-методичного комплекту «Математика. 4 клас. С.О.Скворцова, О.В. Онопрієнко» (підручник у 2-х частинах; навчальний зошит у 4-х частинах; додаток «Працюю самостійно» у 4-х частинах; методичний супровід для учителя).

Тема уроку: Узагальнюємо вивчене про математичні вирази, рівності, нерівності. (с. 127)

  Мета: узагальнити й систематизувати алгебраїчні поняття.  Дидактичні задачі. Узагальнити уявлення про математичні вирази; класифікувати математичні вирази на числові та вирази зі змінною; актуалізувати вміння читати математичні вирази (із застосуванням назви виразу та назв компонентів арифметичної дії); зумовити висновок про неможливість знаходження значення виразу зі змінною без відомого значення змінної. Актуалізувати розуміння залежності значення добутку від зміни одного з множників, застосувати розуміння цієї залежності для одержання певного результату; знання правил порядку виконання дій у виразах із дужками та без дужок; удосконалювати обчислювальні навички та вміння знаходити значення виразів на кілька дій. Удосконалювати вміння знаходити значення виразу зі змінною при заданому значенні змінної; встановлювати залежність значення виразу зі змінною від її числового значення. Актуалізувати поняття рівняння та розв’язку (кореня) рівняння; удосконалювати вміння розв’язувати рівняння і робити перевірку правильності розв’язку; уявлення про нерівності зі змінною. Удосконалювати вміння добирати кілька розв’язків нерівності зі змінною, розв’язувати задачі на знаходження четвертого пропорційного; на пропорційне ділення; на знаходження невідомих за двома різницями. Актуалізувати уявлення про алгебраїчний метод розв’язування задач (для учнів із високим рівнем пізнавальних потреб і можливостей). Удосконалювати вміння знаходити дріб від числа. Розвивальна задача: розвивати варіативне мислення; абстрактне мислення під час розв’язування задач алгебраїчним методом.

Обладнання:  мультимедійний комплект.

                                                     ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Ось і добігає кінця навчальний рік, добігає кінця навчання у початковій школі… Ви вже набули досвіду математичної діяльності у розв’язуванні задач, у виконанні арифметичних дій тощо. І, мабуть, чули, що в основній школі математика розділиться на два предмети – алгебру та геометрію. Відверто кажучи, елементи алгебри ви вже опанували в початковій школі… Сьогодні на уроці ви узагальните і систематизуєте знання алгебраїчного матеріалу, які ви одержали в початковій школі, які є підґрунтям для подальшого навчання в основній школі.

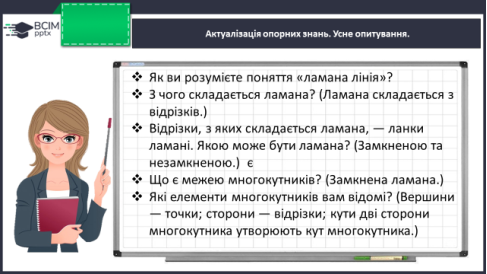
ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1.   Усне опитування. Див. урок №11-13.

2. Математичний диктант.

1. Сума чисел 560 та 280 зменшити 10 разів.
2. Різницю чисел 510 та 170 збільшити в 5 разів.
3. Добуток 270 та 4 зменшити на 80.
4. Частку 640 та 16 збільшити на 290.
5. Перший доданок подано добутком 280 та 3, другий доданок 160, знайти значення суми.
6. Зменшуване 810, від’ємник поданий часткою чисел 960 та 480, знайти значення різниці.
7. Ділене подано добутком 300 та 4, а дільник число 60, знайти значення частки.
8. Перший множник 720, другий множник поданий різницею чисел 560 і 470, знайти значення добутку.
9. Знайти невідоме ділене, якщо дільник 720, а значення частки 4.
10. Знайти невідомий дільник, якщо ділене 720, а значення частки 4.
11.                      Знайти невідомий доданок, якщо значення суми 5600, а відомий доданок 4800.

ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ЗНАНЬ ТА СПОСОБІВ ДІЇ

1. Узагальнення й систематизація знань учнів про числові вирази та вирази зі змінною.

Завдання №1 виконується колективно.

Вдосконалення навичок письмового множення. Завдання №2 виконується з коментарем.

Пригадуємо залежність значення добутку від зміни одного з множників.; залежність значення частки від зміни діленого (дільника); залежність значення суми від зміни одного з доданків; залежність значення різниці від зміни зменшуваного ( від’ємника). Щоб значення добутку зменшилось у 2 рази, достатньо один з множників зменшити в 2 рази.

2. Закріплення правила порядку дій у виразах. Вдосконалення навичок письмових обчислень.

Завдання № 3 виконується учнями з коментарем.

Завдання №4 виконується колективно; пропонується учням з високим рівнем пізнавальних потреб і можливостей.

Аналізуємо у якому порядку виконуються дії у поданому виразі, обчислюємо його значення; пропонуємо різні варіанти зміни порядку дій; з’ясовуємо, що значення добутку (різниці) збільшиться (зменшиться). Висуваємо варіант зміни порядку дій, щоб виконувалась вимога; обчислюємо значення одержаного виразу. Підтверджуємо або спростовуємо гіпотезу.

4.Узагальнення й систематизація знань учнів про рівняння.

Перед виконання завдання проводиться бесіда: Дати означення рівняння. Як ви розумієте «розв’язати рівняння»? Що є розв’язком (коренем) рівняння? Які рівняння ви вмієте розв’язувати? Якими способами можна розв’язати просте рівняння? У чому полягає спосіб добору? Спосіб на підставі правила знаходження невідомого компонента? Спосіб на підставі властивості рівності? Як звести рівняння, в якому права частина або один з компонентів поданий числовим виразом, до простого рівняння? Способи розв’язування рівнянь можна повторити за с. 20-21 підручника ( частина 1).

3. Узагальнення і систематизація знань про нерівності зі змінною. Вдосконалення умінь знаходити кілька розв’язків нерівності зі змінною.

Учні знаходять розв’язки нерівності зручним для себе способом..

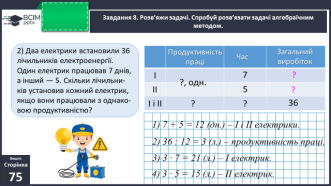Вдосконалення уміння розв’язування задач. Завдання виконується учнями самостійно.

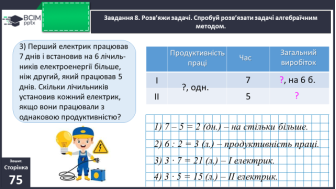
4. Розвиток варіативного мислення учнів.

Завдання №194 із РЗ пропонуємо учням з високим рівнем пізнавальних потреб і можливостей.

Розвязання:

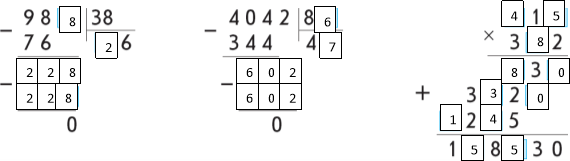
5. Розвиток логічного мислення учнів.

За наявності резерву часу учням з високим рівнем пізнавальних потреб і можливостей пропонуємо задачу:

З чотирьох дівчинок та 3 юнаків треба скласти музичну групу з 4 осіб, в яку входило б не більш ніж 2 дівчинки. Скількома способами це можна зробити?

По-перше , поміркуємо, що означають слова: „ не більш ніж 2 дівчинки”?

В групі можуть бути 2 дівчинки або 1.

Отже, склад групи: 2 дівчинки та 2 юнаки або 1 дівчинка та 3 юнака. Позначимо дівчинок А,В,С,Д, виберемо двох з них:

АВ АС АД ВС ВД СД

Це можна зробити 6 способами.

Позначимо юнаків М,Р,Т, виберемо двох з них: МР МТ РТ . Це можна зробити 3 способами.

Тобто в першому випадку групу можна обрати:

МР МР МР

АВ МТ АС МТ АД МТ РТ                РТ                                          РТ

6 * 3 = 18 способами. У другому випадку:

1 дівчинку з 4-х можна обрати 4 способами, а 3 юнаків з 3 – х лише одним способом. Маємо:

А - МРТ В – МРТ С – МРТ Д – МРТ

Тобто 4 різні групи.

Всього музичних груп можна скласти: 18 + 4 = 22 способами.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Які алгебраїчні поняття ви повторили? Як ви розумієте вираз? Числовий вираз? Вираз зі змінною? Що називається рівнянням? Що означає розв’язати рівняння? Що є розв’язком (коренем) рівняння? Які способи розв’язування простих рівнянь ви знаєте? Як можна міркувати про розв’язуванні складніших рівнянь – в яких права частина або один з компонентів поданий числовим виразом?

Що важливе для вас ми повторили сьогодні на уроці? Що було найцікавішим? Які із завдань ви хотіли б виконувати і в 5 класі?

 Конспект уроку математики з використанням навчально-методичного комплекту «Математика. 4 клас. С.О.Скворцова, О.В. Онопрієнко» (підручник у 2-х частинах; навчальний зошит у 4-х частинах; додаток «Працюю самостійно» у 4-х частинах; методичний супровід для учителя).

Тема уроку: Узагальнюємо вивчене про геометричні фігури

Мета: узагальнити й систематизувати геометричні поняття. Дидактичні задачі. Удосконалювати навички усних обчислень. Узагальнити знання про геометричні фігури; класифікацію геометричних фігур на плоскі та просторові; класифікацію плоских фігур на многокутники та круги; елементи многокутника; класифікацію чотирикутників на прямокутники та непрямокутники; класифікацію прямокутників на власне прямокутники та квадрати; істотні ознаки прямокутника, квадрата. Розвивальна задача: розвивати логічне мислення учнів.

Обладнання:  мультимедійний комплект

Тип уроку: узагальнення й систематизації знань та способів дії

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Предмети, що нас оточують характеризуються такою ознакою як форма. Спостерігаючи різноманітні форми людство винайшло геометричні фігури. Геометричні фігури є образами реальних предметів, що оточують людину. Розділ математики, який вивчає просторові відношення та форми - це геометрія. Власне, геометрію, як окремий предмет ви будете вивчати в основній школі. Тому, сьогодні на уроці ви узагальните і систематизуєте знання елементів геометрії, з якими ви познайомились у початковій школі…

1. Перевірка домашнього завдання ( вибірково)

2. ПОВІДОМЛЕННЯ ТЕМИ УРОКУ ТА МОТИВАЦІЯ НАВЧАЛЬНО – ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІ

1. Усна лічба.

ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ЗНАНЬ ТА СПОСОБІВ ДІЇ

Узагальнення й систематизація знань учнів про геометричні фігури.

Завдання №1 виконується колективно.

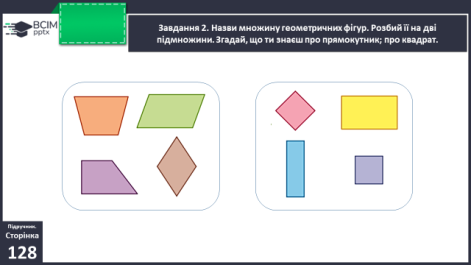
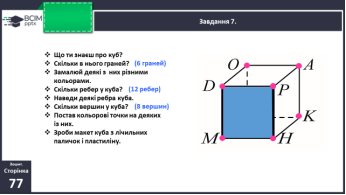
Розбиваємо множину фігур на дві підмножини: просторові фігури та плоскі фігури. Множину плоских фігур розбиваємо на дві підмножини: круги та многокутники. Найменша кількість сторін многокутника – три. Елементи многокутника: сторони – відрізки, вершини – точки, кути.

Завдання №2 виконується колективно.

Множину чотирикутників розбиваємо на дві підмножини: прямокутники і не прямокутники. Пригадуємо означення прямокутника (чотирикутник, в якого всі кути прямі); властивості сторін прямокутника ( протилежні сторони рівні)

та означення квадрата ( прямокутник, в якого всі сторони рівні). Можна зіставити прямокутник і квадрат, використовуючи схему на с. 68 підручника ( частина2).

1. Закріплення поняття периметра і площі прямокутника. Розв’язування задач на застосування формули периметра і площі прямокутника.

Завдання №4 виконується самостійно .

 Завдання № 5 виконується колективно.

На скільки рівних частин розділено ціле? Скільки таких частин зафарбували? Запишіть відповідний дріб. Назвіть чисельник; знаменник. Що означає знаменник? Чисельник?

Отже, дріб – це одна або кілька рівних частин цілого. Дроби записуються двома цифрами. Цифра під рискою – знаменник – означає на скільки рівних частин розділили ціле. Цифра над рискою – чисельник – означає скільки таких частин взяли.

Формування уміння розв’язувати рівняння.

2. Вдосконалення обчислювальних навичок і уміння порівнювати числові вирази.

Завдання № 198 виконується учнями самостійно.

3.   Вдосконалення уміння розв’язувати складені задачі.
4.   Завдання № 199 виконується учнями самостійно .

Розвиток логічного мислення

VІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

• Що важливе для себе ви повторили сьогодні на уроці? Що було найлегшим? Які завдання ви виконували впевнено? Під час розв’язання яких завдань ви потребували допомоги? Які із завдань ви хотіли б виконувати і в 5 класі?

   Конспект уроку математики з використанням навчально-методичного комплекту «Математика. 4 клас. С.О.Скворцова, О.В. Онопрієнко» (підручник у 2-х частинах; навчальний зошит у 4-х частинах; додаток «Працюю самостійно» у 4-х частинах; методичний супровід для учителя).
 

Тема уроку: Узагальнюємо вивчене про дроби (онлайн)

Мета: узагальнити й систематизувати поняття дробу. узагальнити й систематизувати поняття дробу. Дидактичні задачі. Удосконалювати навички усних обчислень. Актуалізувати спосіб одержання дробу; вміння читати й записувати дроби; уявлення про чисельник і знаменник дробу; уміння порівнювати дроби за величиною; спосіб порівняння дробів із рівними знаменниками; закріплювати вміння записувати дроби в порядку зростання; спосіб знаходження дробу від числа; спосіб знаходження числа за величиною його дробу; уміння застосовувати правило знаходження дробу від числа під час розв’язування задач. Удосконалювати вміння розв’язувати складені задачі, що містять знаходження дробу від невідомого числа.  Розвивальна задача: розвивати логічне мислення учнів.

Обладнання:  мультимедійний комплект.

Тип уроку: узагальнення й систематизації знань та способів дії

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

На минулому уроці ми повторили знання про геометричні фігури. Зазначимо, що геометрія пов’язана із вимірюванням та обчисленням геометричних величин. Для вимірювання величин людство винайшло певні мірки – одиниці вимірювання. Результати вимірювання спочатку записувались натуральними числами – числами, які використовуються у лічбі…Але, часто траплялись такі випадки, коли на певній величині, наприклад на довжині, не можна було укласти ціле число мірок, тому люди винайшли числа особливого виду – звичайні дроби, знання про які ви так само, узагальните і систематизуєте сьогодні на уроці.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА СПОСОБІВ ДІЇ

Усне опитування.

ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ЗНАНЬ ТА СПОСОБІВ ДІЇ

Узагальнення й систематизація знань учнів про дроби. Завдання № 1 виконується колективно на онлайн уроці.

На скільки рівних частин розділено ціле? Скільки таких частин зафарбували? Запишіть відповідний дріб. Назвіть чисельник; знаменник. Що означає знаменник? Чисельник?

Отже, дріб – це одна або кілька рівних частин цілого. Дроби записуються двома цифрами. Цифра під рискою – знаменник – означає на скільки рівних частин розділили ціле. Цифра над рискою – чисельник – означає скільки таких частин взяли. Завдання виконується колективно на онлайн уроці.

Пригадуємо як можна міркувати при порівнянні дробів з рівними знаменниками ( із двох дробів з рівними знаменниками більше той, в якого чисельник більший і навпаки; або спочатку взяли … частин, а потім … таки частин; порівнюємо числа частин і робимо висновок).

Завдання №2, 3 виконується колективно.

Пригадуємо правило знаходження дробу від числа та числа за величиною його дробу.

7. Вдосконалення уміння розв’язувати складені задачі, що містять знаходження дробу від числа.

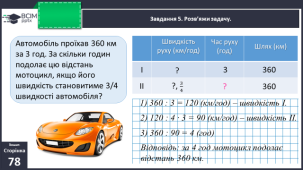
Завдання виконується колективно.

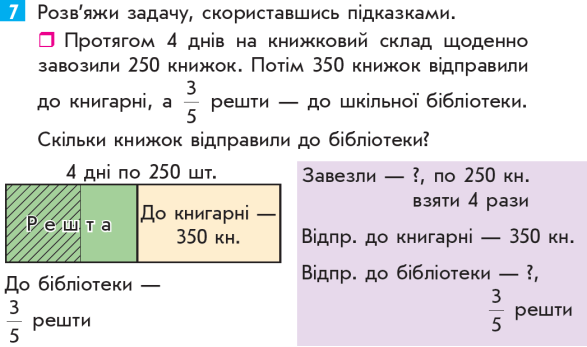
За коротким записом поясніть числа задачі. Що означає число 250? Число 4?

Число 350? Що означає число

3 ? ( Яку частину від решти відправили до

5

бібліотеки.)Що означає знаменник 5? ( На скільки рівних частин поділили решту книжок.)Що означає чисельник 3? ( Що 3 такі частини віддали до бібліотеки.) Яке запитання задачі?

• Що треба знати, щоб на нього відповісти? ( Треба знати два числові значення: 1 – скільки книжок залишилось після відправки до книгарні, невідомо, та ІІ –

яку частину становить книжки, що відправило до бібліотеки, відомо

3 . )Як

5

відповімо на запитання задачі? (Розділимо на знаменник і помножимо на чисельник.)Чи можна відразу відповісти на запитання задачі? ( Ні, ми не знаємо решту книжок.)

• Що треба знати. Щоб про це дізнатися? ( Треба знати два числові значення: 1 – скільки всього книжок завезли на склад , невідомо; та П – скільки книжок відправили до книгарні, відомо 350.)Якою арифметичною дією відповімо на це запитання? ( дією віднімання.)Чи можна відразу відповісти на запитання задачі? ( Ні, ми не знаємо, скільки всього книжок завезли на склад.)
• Що треба знати, щоб про це дізнатися? ( Треба знати два числові значення: 1

– скільки книжок привозили щодня, відомо, 250; та П – скільки днів, відомо 4

дні.) Як відповімо на це запитання? ( Дією множення. )Чи можна відразу відповісти на запитання задачі? ( Так.) Аналіз закінчено.

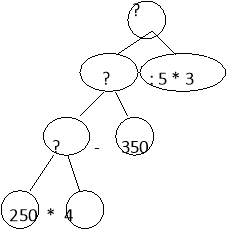
• Складіть план розв’язування задачі. Запишіть розв’язання по діях і виразом. Завдання №4 виконується в парах

Завдання № 202 із РЗ виконується учнями самостійно.

8.   Формування уміння розв’язувати рівняння. Завдання № 5 виконується учнями самостійно.
9. Розвиток логічного мислення учнів.

Як переправитися трьом розбійникам і трьом мешканцям міст через річку в двомісному човні без того, хто переправляє, якщо не можна залишати на одному березі розбійників більше, ніж мешканцям міста?

Розв’язання. Позначимо: Р – розбійники, М – мешканці міста. Одну переправу будемо позначати наступним чином:

1. стрілка показує напрям руху;
2. літери на стрілці показують, хто переправляється;
3. зліва записуються усі, хто в дану мить залишися на лівому березі;
4. справа записуються усі ті, хто в дану мить вже переправився.

В цій задачі спочатку можуть переправитися 2 розбійника, тоді над стрілкою, яка вказує напрям руху ми запишемо РР; на лівому березі залишилися 3 мешканця міста і 1 розбійник, значить, зліва від стрілки ми запишемо МММР. На правому березі поки нікого немає, тому, нічого не пишемо.

1. МММР РР
2. МММР Р Р

3. МММ РР Р
4. МММ Р РР

5. МР ММ РР

6. МР МР МР

7. РР ММ МР

8. РР Р МММ

9. Р РР МММР

10. Р Р МММР

11. РР МММР

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №85 – розв’язати рівняння.

VІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

• Що важливе для себе ви повторили сьогодні на уроці? Що було найлегшим? Які завдання ви виконували впевнено? Під час розв’язання яких завдань ви потребували допомоги? Які із завдань ви хотіли б виконувати і в 5 класі?