9-кл.Алгебра .Презентація:,,Означення та властивості геометричної прогресії".

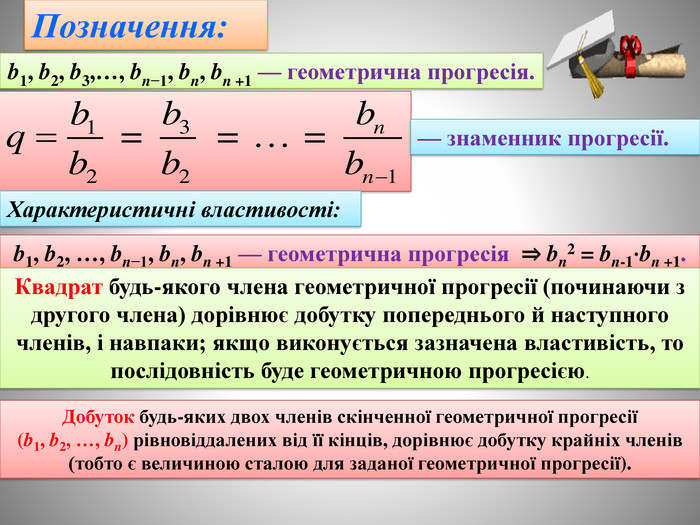
Презентація. Вчителя математики. Ворохтянської ЗОШ I-III cт. Будзуляк і.і.

Розділ 3. Числовіпослідовності.§18 9-клас. Алгебра. За підручиком О. С.Істер

Урок № 54 Розділ 3. Тема: §18. Геометрична прогресія, її властивості. Формула n-го члена геометричної прогресії.

КОМПЕТЕНТНІСТЬОБДАРОВАНІСТЬРАДІСТЬУСПІХУРОК

Тип уроку : Засвоєння знань,вироблення вмінь. Обладнання: Мультимедійна дошка,проектор.

Формувати вміння розв’язувати вправи на застосування формул геометричної прогресії , уміти свідомо застосовувати їх для розв’язування задач. Ознайомленя учнів із означення геометричної прогресії,відповідної термілогії,її рекурентної формули та основних властивостей. Розвивати навчальні інтереси ,здібності на основі розумових дій;формувати навички аналізу,систематизації,узагальнення. Розвивати увагу. Мета уроку:

“Бліц - опитування ”1. Серед наведених послiдовностей виберiть «зайву»:1) 1; 2; 3; 4;… 2) 2; 4; 6; 8;… 3) 2; 4; 8; 16;… 4) 3; 7; 11; 15;…Проаналiзуйте, в чому полягає вiдмiннiсть цiєї послiдовностi від iнших.2. Як записати для арифметичної прогресiї (xn) iз різницею m:1) формулу n-го члена;2) формулу суми її перших n членiв?

Геометрична прогресiя. Означення. Геометричною прогресiєю називається числова послiдовнiсть, перший член якої вiдмiнний вiд нуля, а кожний член, починаючи з другого, дорiвнює попередньому члену, помноженому на одне й те ж саме число, що не дорiвнює нулю. Це постiйне для заданої послiдовностi число q називається знаменником геометричної прогресiї. Приклад: 2, 6, 18, 54, 62, … (q = 3);Знаменник (q) геометричної прогресії можна знайти,якщо будь-який член прогресії,починаючи з другого,подвлити на попередній.

Позначення:b1, b2, b3,…, bn−1, bn, bn +1 — геометрична прогресiя.— знаменник прогресiї. Характеристичнi властивостi:b1, b2, …, bn−1, bn, bn +1 — геометрична прогресiя ⇒ bn2 = bn‑1⋅bn +1. Квадрат будь-якого члена геометричної прогресiї (починаючи з другого члена) дорiвнює добутку попереднього й наступного членiв, i навпаки; якщо виконується зазначена властивiсть, то послiдовнiсть буде геометричною прогресiєю. Добуток будь-яких двох членiв скiнченної геометричної прогресії (b1, b2, …, bn) рiвновiддалених вiд її кiнцiв, дорiвнює добутку крайніх членiв (тобто є величиною сталою для заданої геометричної прогресiї).

Виконання усних вправ1. Чи є послідовність (xn) геометричною прогресiєю?1) 3; 3; 3; 3; 3; 2) 2; 0; 0; 0; 0; 3) 3; 6; 12; 24; 48. Виконання письмових вправ.( РОБОТА З ПІДРУЧНИКОМ ).№ 765 (1). Знайдіть першi чотири члени геометричної прогресії (bn) зі знаменником q , якщо: Вiдповiдь: 10; 20;40; 80.№ 767 (хn) - геометричної прогресії зі знаменником q , якщо:

№ 769 (2). Послідовність(bn) – геометрична прогресія знайдіть: Вiдповiдь: - 1. № 773 (2). Знайдіть перший член геометричної прогресії (bn) ,якщо : Вiдповiдь: 3.

Тестовi завдання1. Чому дорiвнює перший член геометричної прогресiї (bn), якщо b2 = 54, а знаменник q = 6?А) 48; Б) –1; В) 2; Г) 1.2. Яка з наведених послiдовностей є геометричною прогресiєю?А) 2; 5; 8; 11; Б) 2; 6; 18; 36; В) 2; –4; 8; –16; Г) 2; 4; 12; 48.

Домашнє завдання. Р.3 § 18. Вивчити означення понять, розглянутих на уроцi. Виконати вправи :№ 766(2) , № 768 (3 ), № 770( 2), срт.175. № 774. стр.175( додатково. )

Підсумок уроку.1. Під час проведення уроку мені сподобалось2. Свої знання япоповнив …3. Я добре виконав … 4. Я вважаю, що поставлену мету ми…виконали …

МОЛОДЦіДякую за урок!