Математичний квест до тижня математики

 

 

 

 

 

 

Математичний квест

 для учнів 5-9 класів

( до тижня математики)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Методичні рекомендації і правила проведення квесту

Математичний квест проводиться протягом дня. Завдання на тури  по QR кодах учні знаходять  на перервах. Також на перервах  приймаються, заслуховуються та оцінюються виконання завдань вчителем або асистентом( старшокласником). До гри запрошуються 15 учасників (по три найсильніших учня із 5-9 класів). Решті учнів пропонується взяти участь у «пошуку кращої оцінки». Для цього треба у приміщені школи відшукати розміщені ребуси (додаток 1) та скласти із них вислів. За кожен відгаданий ребус учень отримує сертифікат на право додаткового балу на уроці математики. Якщо гравець відгадав усі ребуси та із слів склав вислів про математику, він отримує сертифікат на 12 балів з будь якого уроку математики, окрім контрольної роботи. Для активізації учнів ребуси слід розміщувати порційно (по 3-4 перед кожною перервою) у незвичних для оголошень місцях (вікно, плафон, двері, стіна) та обмежити кількість правильних відповідей на один ребус. Наприклад, після 2-3 правильних відповідей ребус знімається.

І тур. Спритність. Кожному із учасників дається конверт із завданням, що містить три задачі та ключ (додаток 2) (ключ – це український алфавіт з порядковим номером кожної літери).Завдання мають бути підібрані відповідно за віком і однакові за складністю, окремо для кожного класу.  Розв’язавши три завдання, учасник знає три числа, які співставивши із ключем можна скласти слово. Із відповіддю треба підійти до визначеного місця, де будуть лежати 10 конвертів. На кожному із них написані ключові слова, побачивши своє слово на конверті, гравець бере його. Це і є перепусткою до ІІ туру. Вибувають п’ятеро учасників, які пізніше прибули за конвертом, або прибули з неправильним кодовим словом.

ІІ тур. Домашнє завдання. У цьому турі бере участь 10 гравців – по два із кожного класу. В конвертах, які отримали гравці з І туру, знаходяться імена  або портрети видатних математиків: Кравчук – 5 клас, Архімед – 6 клас, Декарт – 7 клас, Вієт – 8 клас, Піфагор – 9 клас. Завдання кожного з учасників до великої перерви відшукати та підготувати про дану людину цікаве повідомлення та представити його на суд глядачам та жюрі. Вибуває два учасники, які найгірше впорались із завданням.

ІІІ тур. Поетичний. Для кожного із восьми учасників підготовлено аркуш із віршем про математику, але всі слова у даному творі переставлені місцями. Завдання гравців полягає в тому, щоб якнайшвидше із даних слів скласти вірш.  У фінал виходять шестеро учнів, які найкраще впорались із завданням (додаток 3).

Фінал. Для визначення найкращого математика школи після уроків проводиться вікторина, яка складається із трьох етапів: практичний, художньо-естетичний та теоретичний  (додаток 4).

Для оцінювання завдань І – ІІІ турів та фінальної гри у члени жюрі слід залучити вчителів математики та рідної мови.  

Додаток 1

 

________________________________________________________________________

 

________________________________________________________________________

 

                                   о=е

^{____________________________________________________________}

 

 

                               

                             

 О = Е

______________________________________________________________

 

                                і

________________________________________________________

                                                                    

____________________________________________________________________

Розв’яжи приклад. Відповідь вкаже на порядковий номер літери в українському алфавіті.

168291-(3451875:25+271854:9)

_____________________________________________________________

              

                                     У = А                       Н = К                     Й = Ю

_____________________________________________________________

Розв’яжи приклад. Відповідь вкаже на порядковий номер літери в українському алфавіті.

(25²+75):70+2

__________________________________________________________________

 

                                                                       

                                    

_________________________________________________________________

(Процвітання та інтереси держави тісно пов’язані з математикою і добробутом)

Додаток 2

Завдання для проведення І туру.

Завдання для 5 класу

1. Об’єм прямокутного паралелепіпеда дорівнює 9936м³. Яка його висота, якщо довжина дорівнює 27м, а ширина на 11м менша від довжини?
2.   У мішку було 75кг борошна. Скільки борошна у мішку залишилось після того, як з нього тричі відсипали по 17кг?
3.     У трьох ящиках було 70кг яблук. У другому ящику яблук було вдвічі більше, ніж в першому, а в третьому – на 5кг менше, ніж в другому. Скільки кілограм яблук було у першому ящику?

Відповідь. 23   24   15    (тук)

Завдання для 6 класу

1.   Знайдіть невідомий член пропорції:
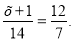
2.   У 5% розчин солі масою 300г досипали 75г солі. Знайдіть відсотковий вміст солі у новому розчині.
3.   Довжина городу прямокутної форми дорівнює 60м. Господар відвів під жито 70% площі поля, а решту 378га – під картоплю. Яка ширина городу?

Відповідь. 23   24   21   (тур)

Завдання для 7 класу

1.   Один із гострих кутів прямокутного трикутника дорівнює 67⁰. Знайдіть величину іншого гострого кута.
2.   Розв’яжіть рівняння: х² + (-4 - х)(-4 + х) = 8(х + 1).
3.   Точки A, B, C, D лежать на одній прямій так, що АВ=10см, АС=3см, ВD=4см. Яку найбільшу довжину може становити відрізок СD?

 Відповідь. 23   1   17   (там)

Завдання для 8 класу

1.    Якого найменшого цілого значення може набувати четверта сторона чотирикутника, якщо три інші відповідно дорівнюють 7см, 9см та 8см?
2.    Розв’яжіть рівняння:
3.    У паралелограмі АВСD бісектриса кута А перетинає сторону ВС у точці К. Знайдіть АD, якщо АВ=4см, КС=11см.

Відповідь. 23   1   15   (так)

Завдання для 9 класу

1.   Знайдіть найменший цілий розв’язок нерівності
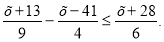
2.   Обчислити площу трикутника зі стороною с=6см, та прилеглими до неї кутами α=70⁰, β=60⁰. Відповідь округлити до цілих.
3.   Визначте відстань між точками А(-5; -7) та В(3; 8).

Відповідь. 23   19   17   (том)

Додаток 3

Завдання для ІІІ туру  (зібрати вірш). Учням необхідно  спочатку зачитати  вірш про математику, а слова переставити тільки у рядочках.

Якщо хочеш досягнути

У житті своїм вершин,

Математику збагнути

Мусиш тонко, до глибин.

Калькулятор і комп'ютер —

Хто сьогодні їх не зна,

Та за пояс їх заткнути

Може світла голова.

Якщо хочеш бізнесменом

Після школи, друже, стать,

Аксіоми й теореми

Мусиш добре пам'ятать.

Якщо лікарем ти станеш,

То, колего, тут затям,

Коли десь ти помилишся —

Хтось поплатиться життям.

Не кажу про космонавтів,

Вчителів і моряків...

То, коли чогось не знав ти,

Час це вивчити настав.

Не махай на все рукою,

Не лінуйся, а учись.

Бо чого навчишся в школі,

Знадобиться ще колись.

 

хочеш  якщо  досягнути

у вершин житті своїм,

збагнути математику

тонко мусиш  глибин до.

 

комп'ютер калькулятор і

 зна сьогодні хто не їх

пояс та за заткнути їх

світла голова може 

 

хочеш  бізнесменом якщо

школи стать після  друже 

теореми аксіоми й

мусиш пам'ятать добре

 

 ти лікарем станеш якщо

затям то тут колего

ти коли помилишся десь

життям поплатиться хтось

 

не  космонавтів про кажу

вчителів моряків і

чогось то коли не ти знав

час  настав вивчити це

 

махай не  рукою все на 

лінуйся а не  учись

бо в школі чого навчишся

ще колись знадобиться 

Додаток 4

Практичний тур.

1. Сірникова головоломка. Учням пропонується скласти із сірників чи рахувальних паличок вираз. Необхідно перекласти один сірник так, щоб рівність була правильною.

Відповідь:   1) 13 – 7 = 6

                    2) 6 = 5 + 1

            3) 11 – 6 = 5

 

 

 

 

 

2. Зважувальна головоломка. Кожному з учасників дається лабораторні терези та 9 монет. Одна з них фальшива, вона легша за справжні. Як за допомогою двох зважувань виявити фальшиву монету? Монети можна замінити шротом, пластиліном або іншими дрібними предметами.

Відповідь. Перше зважування: на кожну чашку терезів кладемо по три монети. Якщо шальки врівноважені, то для зважування беруться дві із трьох монет, що залишилися. Якщо фальшива монета на терезах, то ясно, на якій вона чаші терезів. Якщо ж терези врівноважені, то фальшивою є незважена монета. Якщо при першому зважуванні одна із чаш переважує іншу, то фальшива монета там, де вага виявляється меншою. Тоді другим зважуванням встановлюємо яка із монет є фальшива.

3. Переливальна головоломка. Кожному учаснику на стіл ставиться трилітрова банка води й дві порожні банки: одна – літрова, друга – дволітрова. Пропонується розлити воду так, щоб в усіх банках було по одному літру води.

Відповідь.

І спосіб				І спосіб
№ переливання	Банка на 3 л	Банка на 2 л	Банка на 1 л	№ переливання	Банка на 3 л	Банка на 2 л	Банка на 1 л
0	3	0	0	0	3	0	0
1	1	0	2	1	2	1	0
2	1	1	1	2	2	0	1
-	-	-	-	3	1	1	1

 

Художньо-естетичний тур.

1. Показуха. Один із асистентів ведучого мімікою зображає, наприклад, математичні об’єкти: трикутник, круг, аксіома, циркуль, формула, транспортир. Завдання фіналістів вгадати показаний об’єкт.

2. Художники. В цьому конкурсі фіналісти за визначений час мають намалювати на плакаті малюнок, який складається з геометричних фігур, наприклад, годинник. Яскравість конкурсу полягає в тому, щоб кожен із фіналістів намалював одночасно два однакових малюнки один лівою рукою, інший – правою.

Теоретичний тур.

Бал дається за правильну відповідь. Час для розмірковування – 30с. Відповіді фіналісти пишуть на картках та показують по команді членам журі. Завдання слід підбирати враховуючи вік дітей, які вийшли у фінал.

Перелік можливих завдань для фінальної гри.

1. Який видатний математик був олімпійським чемпіоном?         (Піфагор)

2.  Який видатний математик створив свою партію, члени якої носили на грудях п’ятикутну зірку?                                                                           (Піфагор)

3. Скільки натуральних дільників у числа 1?                                   (1)

4. Скільки кратних у числа 1?                                                              (Безліч)

5. Скільки дільників у числа 0?                                                        (Безліч)

6. Скільки кратних у числа 0?                                                           (Жодного)

7. Хто перший ввів число π?                                                            (Архімед)

8. Як називається рівність двох відношень?                                (Пропорція.)

9. Що спільного у геометрії та землі? (Геометрія – з грецької – землемірство)

10. Алгебра – це наука про…                                  (... розв’язування рівнянь)

11. Кожна людина колись стоїть перед вибором. Коли треба погоджуватись, а коли й відмовлятись. Нажаль при прийнятті якогось рішення ми керуємося не тільки розумом, але й емоціями відчуттям…Не завжди і на запитання взагалі можемо відповісти. Тож скажіть, будь ласка, на яке запитання не можна відповісти «Так»?              (ти зараз спиш?)

12. Ми живемо у тривимірному просторі, де можна практично все виміряти. Та є такі величини, які не мають довжини, ширини, висоти, а їх можна виміряти. Які це величини? (час, тиск, температуру…)

13. А ще однією із таких величин, що не мають висоти, ширини та довжини є тривалість місяців. Назвіть скільки місяців у році мають 28 днів?           (усі 12)

14. А тепер запитання про друзів наших менших. Собака був прив’язаний до 10-ти метрової мотузки, а пройшов 300м. Як це йому вдалось?         (мотузка не прив’язана, або рухався по колу)

15.Нам у житті зустрічаються різні люди, та все ж найбільш комфортніше почуваємося з тими, що говорять лише правду. Нажаль трапляється таке не завжди. У місті І мешканці говорять тільки правду, у ІІ-му – тільки неправду, а у ІІІ-му – почергово правду і неправду. До пожежної частини подзвонили та сказали: «У нас пожежа». У яке місто слід виїхати пожежникам?                  (нікуди)

16. Людство завжди помічало магію цифр та чисел. Наприклад Піфагор вважав число 7 – щасливим, у наш час 13 – є неприємним числом, а у давньому Вавилоні деяке число вважали «священним». Звідси і пішов поділ року на місяці, доби на години, години на хвилини. Що це за число?         (12)

17. Вивчаючи у 5 класі натуральні числа ми взнали, що не у всіх країнах цей ряд однаковий. Принаймні він відрізняється однією цифрою. Дано числа 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Що більше їх сума, чи їх добуток? (сума 45, а добуток - 0)

18. Всі про неї чули, читали, або дивились мультфільм. Як звати дівчинку, висота якої становить 2,5 см?           (Дюймовочка)

19. Щоб порозумітися з іншою людиною ми маємо намагатись бути конкретними у своїх висловлюваннях. Наприклад, попереджуючи про зустріч нам необхідно вказати хоча би дату, чи назву дня. Назвіть п’ять днів підряд, не називаючи ні чисел місяця, ні днів тижня.   (позавчора, вчора, сьогодні, завтра, післязавтра)

20. Часто учні роблять помилки в обчисленнях, хоча відповідь виходить вірна. Так і зараз замість того, щоб додати три цифри, учень їх помножив, а результат вийшов такий же. Які це цифри?            ( 1, 2, 3)

21. Українці, які поважають свою країну, стараються позбутися «суржику». Скажіть, будь ласка, як вірно сказати: «7 плюс 5 дорівнює адінадцать» чи «7 плюс 5 дорівнює одинадцять»?          (12)

22. Кожен з вас вміє тримати ножівку  у руках. Тож скажіть, будь ласка, якщо від чотирикутної дошки відпиляти один із кутів, скільки кутів залишиться?  (5)

23. Усі без винятку учні колись замість дії піднесення до квадрату виконували дію множення. Тож будьте зараз уважні. Два в квадраті – чотири, три в квадраті – дев’ять, а кут у квадраті дорівнює … (90⁰)

24. З кожним роком у селі все більше тракторів, а все менше коней. Але кожного ранку, йдучи до школи, ми бачимо пана  Володимира, який на своїх двох вірних кониках збирає по селі молоко. Отже пара коней пробігла 10 км. Скільки пробіг кожен кінь?      (10 км)

25. Всі учні школи дуже люблять урок фізкультури. На початку уроку Микола Анатолійович вишикував учнів у шеренгу довжиною 7 метрів на відстані 1м один від одного. Скільки учнів було у класі?          (8)

26. Оточення відомого математика Джона Непера будо впевнене в тому, що той таємно займається чорною магією та зв’язаний зі Старим Ніконом (так у Шотландії називали диявола). Якось у будинку сталася пропажа. Підозра впала на слуг. Тоді Непер оголосив, що на винуватого вкаже чорний півень. Для цього він обсипав його попелом та пустив до слуг у темні кімнату. Кожен мав торкнутися півня. Як математик взнав хто злодій?   (у злодія руки були не в попелі).

27. Уранці сторож повідомив господарю про крадіжку. «Як це сталось?» - спитав детектив.

- Я знаходився у східному крилі будівлі, коли почув шелест у західній частині контори. Я побіг туди. Двері були зламані, але я побачив, що якийсь чоловік сідає до машини. Розгледіти я його не міг, адже сонце сліпило мені очі.

Хто злочинець і чому?        (сторож співучасник, на заході вранці сонця не буває)

28. Розгніваний клієнт, побачивши у чашці кави муху, повернув її назад. Через деякий час йому знову принесли горнятко кави. Зробивши тільки один ковток, клієнт зрозумів, що кава таж сама, з горнятка дістали тільки муху, а каву підігріли. Як це йому вдалось?          (перед тим, як повернути каву, він її посолодив)

29. З матеріалів дедективної справи: «Того дня о 10 год вечора йшов дощ, а через 48 годин була сонячна погода». Чи правдива ця інформація?    (ні. Буде знову вечір)

30. Тетяна та Марічка – дуже правдиві дівчатка. Вони говорили неправду тільки в день свого народження. 6 квітня їх запитали про дату народження, нащо Тетяна відповіла: «Вчора», а Марічка: «Завтра». 7 квітня запитання повторили, але відповідь була такою самою. Коли насправді у них день народження?       (У Тетяни – 6 квітня, а у Марічки 7 квітня).