Алгоритми розв’язування задач з математики

Вступ

 

   Розв’язування  задач  з  математики – це  один  з  пособів  формування  в  учнів  умінь  і  навичок,  отриманих  в  прцесі  вивчення  матеріалу.  Існує  багато  методів  навчання  розв’язувати  задачі  і  вправи.  Можна  виділити  5  основних  та  дати  коротку  їх  розшифровку.

1.              Репродуктивний  метод.

Учитель  показує  алгоритм  розв’язування  задачі  або  вправи  на  на  конкретних  прикладах,  а  учні  самостійно  розв’язують  задачі  певного  типу,  діючи  за  зразком.

2.  Евристичний  метод.

    Учитель  ознайомлює  учнів  із  загальним  правилом  розв’язуванням  задач,  але  не  називає  конкретно  метод  конструювання  алгоритму  розв’язування  задачі  та  область  пошуку  інформації.

3. Конструктивний  метод.

 Дається  вказівка  учням  на  загальний  метод  пошуку  математичних  закономірностей  і  метод  конструювання  алгоритму  розв’язування  задачі.

4. Проблемний  метод.

 Вчитель  створює  проблемну  ситуацію,  а  учні,  знаючі  математичні  закономірності  і,  не  знаючи  програми  розв’язування  задачі,  самостійно  знаходять  конкретний  алгоритм  розв’язку.

5.Дослідницький,  творчий  метод.

 Перед  учнями  ставиться  задача,  а  учні  не  знаючи  алгоритму  розв’язування,  програми  і  методів  пошуку  інформації,  повинні  самостійно  розв’язати  задачу.

   На  практиці,  як  правило,  вчителі  застосовують  найчастіше  перший  і  другий  методи.  Перший  метод  дає  можливість  досягти  мети  і  учні  при  достатній  кількості  вправ  навчаються  розв’язувати  типові  задачі.  Другий  метод  малоефективний,  тому,  що  в  учнів  виникають  труднощі,  якщо  задача  не  підходить  під  типовий  алгоритм.  Решта  методів,  як  правило,  не  застосовують  тому,  що  в  учнів  не  сформовані  вміння  шукати  потрібну  інформацію  та  конструювати  алгоритм  розв’язування  задачі.           

 

 

 

6 клас

Подільність чисел

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

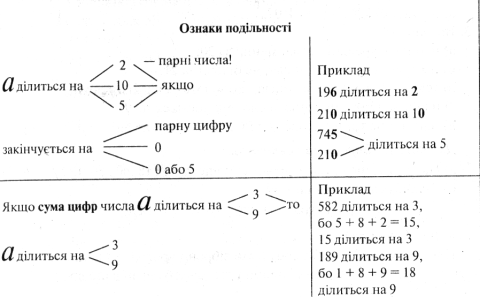
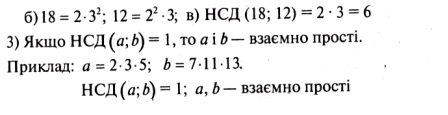
Звичайні дроби

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Відношення і пропорції

 

 

 

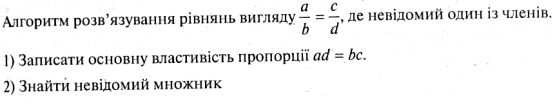
Раціональні числа

 

 

 

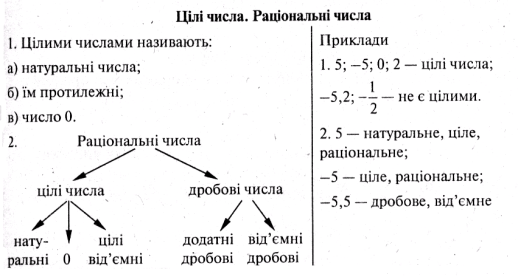
Додавання чисел з однаковими знаками

1. Знайти модулі чисел, що додаються;
2. Дані модулі додати;
3. Перед здобутою сумою поставити їх спільний знак.

          Наприклад:

 

    +20 +(+15)=+(І+20І+І+15І)=+(20+15)=+35

 

        -20 +(-15)=-(І-20І+І-15І)=-(20+15)=-35

 

 

 

 

 

 

Додавання чисел з різними знаками

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7. клас

Лінійні  рівняння  з  однією  змінною

 

Алгоритм №1

 

1.Перенесіть  доданки,  які  містять  невідоме  у  ліву  частину  рівняння,  а  відомі - у  праву,  змінивши  їхній  знак  на  протилежний.

2.Виконайте  зведення  подібних  доданків.

3.Поділіть  ліву  та  праву  частини  рівняння  на  коефіцієнт  при  невідомому,  якщо    він  не  дорівнює  нулю.

4.Запишіть  відповідь. 

 

Алгоритм №2

 

1.Розкрийте  дужки.

2.Перенесіть  невідомі  доданки  у  ліву  частину  рівняння  відомі – у  праву,  змінивши  їхній  знак  на  протилежний.

3.Виконайте  зведення  подібних  доданків.

4.Поділіть  ліву  та  праву  частини  рівняння  на  коефіцієнт  при  невідомому,  якщо  він  не  дорівнює  нулю

5.Запишіть  відповідь.

 

Алгоритм №3

 

1.Знайдіть  найменший  спільний  знаменник  всіх  дробів.

2.Домножте  кожний  член  рівняння  на  найменший  спільний  знаменник  та  скоротіть  дріб.

3.Розкрийте  дужки,  якщо  вони  є.

4.Пернесіть  доданки,  які  містять  невідоме,  у  ліву  частину  рівняння,  а  відомі- у  прву,  змінивши  знаки  на  протилежні.

5.Виконайте  зведення  подібних  доданків.

6.Поділіть  ліву  та  праву  частини  рівняння  на  коефіцієнт  при  невідомому,  якщо  він  не  дорівнює  нулю.

7.Запишіть  відповідь.

 

Розв’язування  задач

Алгоритм №1

(на  складання  рівняння )

 

1.Зробіть  аналіз  умови

2.Перекладіть  задачу  із  звичайної  мови  на  мову  алгебраїчну

3.Невідому  величину  позначить  через  Х.

4.Встановіть  залежність  між  даними  задачі  та  змінною.

5.Складіть  рівняння  та  розв’яжіть  його.

6.Запишіть  відповідь.

 

Алгоритм №2

(на  складання  системи  рівнянь )

1. Зробіть  аналіз  умови.
2. Виділіть   дві  ситуації.
3. Перекладіть  задачу  із  звичайної   мови  на  мову алгебраїчну.
4. Введіть  змінні.
5. Встановіть  залежність  між  даними  задачі   та  змінними.
6. Складіть рівняння.
7. Розв’яжіть  систему  рівнянь.
8. Запишіть відповідь.  

 

Множення одночленів.  Піднесення одночлена  до  степеня.

Алгоритм №1

1. Знайдіть  добуток  коефіцієнтів.
2. Показники степенів  однакових  змінних  додайте.
3. Якщо  змінна  входить  лише в  один  з  множників, то   допишіть  її  у  добутку.

 

Алгоритм №2

1. Піднесіть  до  степеня    коефіцієнт  одночлена.
2. Показник   степеня   кожної змінної  одночлена  помножте  на  показник   степеня,  до  якого  підноситься   одночлен.

 

 

 

Многочлени

Алгоритм №1

( додавання  многочленів )

1. Запишіть  послідовно  у  вигляді  алгебраїчної  суми  всі  члени  многочленна.
2. Зведіть  подібні  доданки.

Алгоритм №2

( віднімання  многочленів )

1. Знайдіть  або  складіть  різницю  многочленів,  беричу  другий  многочлен  у дужи  зі  знаком  мінус  перед  ним.
2. Розкрийте  дужки,  змінюючи  перед  одного членами,що  стоять  у  дужках,  на  протилежні.
3. Зведіть  подібні  доданки.

Алгоритм № 3

(добуток  одночлена  на  многочлен )

1. Помножте  одночлен  на  кожний  член  многочленна.
2. Додайте  одержані  добутки.
3. Виконайте  зведення  подібних  доданків.

Алгоритм № 4

( добуток  многочленна  на  многочлен )

1. Помножте  кожний  член  першого  многочлена  на  кожен  член  другого  многочлена.
2. Додайте  одержані  добутки.
3. Виконайте  зведення  подібних  доданків.

Алгоритм № 5

     (розкладання  многочленна  на  множники ) 

1. Винести  спільний  множник  за  дужки,  якщо  він  є.
2. Зробити  спробу  застосувати  формули  скороченого  множення.
3. Застосувати  спосіб  групування,  якщо  попередні  способи  не  дали  результату.

 

 

Системи рівнянь

Алгоритм № 1

(побудови  графіка  лінійного  рівняння  з  двома  змінними )

1. Знайдіть  значення  У,  якщо  Х=0.
2. Знайдіть  значення  Х,  якщо  У=0.
3.    Зобразіть  на  координатній  площині  точки  А  ( 0;  У )  і 

В ( Х; 0 ).

4. Проведіть  пряму  через  дві  точки.

 

 

Алгоритм № 2

1. Побудуйте  графік  кожного  рівняння  в  одній  системі  координат.
2. Знайти  точки  перетину  графіків.
3. Запишіть  координати  даної  точки.

 

Алгоритм №3

( спосіб  алгебраїчного  додавання )

1. Зрівняйте  коефіцієнти  при  змінній  Х  або  У  так,  щоб  вони  стали  протилежними  числами.
2. Складіть  почленно   ліві  та  праві  частини  одержаних  рівнянь.
3. Розв’яжіть  рівняння  з  однією  змінною.
4. Знайдене  значення  змінної  підставте  у  будь-яке  рівняння  системи.
5. Знайдіть  значення  другої  змінної.
6. Запишіть  відповідь.

 

Алгоритм № 4

( спосіб  підстановки )

1. Виразіть  в  одному  із  рівнянь  одну  змінну  через  іншу  ( Х  через  У,  або  У  через  Х ).
2. Підставте  її  значення  у  друге  рівняння.
3. Розв’яжіть  рівняння  з  однією  змінною.
4. Знайдіть  значення  другої  змінної.
5.    Запишіть  відповідь.

 

 

 

 

 

Раціональні  вирази 

 

Алгоритм № 1

( ділення  степенів )

1. Основу  запишіть  без  змін.
2. Від  показника  степеня  діленого  відніміть  показник  степеня  дільника.

 

Алгоритм № 2

( ділення  одночлена  на  одночлен )

1. Виконайте  ділення  коефіцієнта  діленого  на  коефіцієнт  дільника.
2. Виконайте  ділення  степенів  з  однаковими  основами.
3. До  одержаного  коефіцієнта  допишіть  множники,  одержані  при  діленні  степенів.
4. Відповідь.

 

 

 

 

 

 

 

 

 

 

 

 

8 клас

Алгебраїчні  дроби

 Алгоритм  №1

( додавання  та  віднімання  дробів )

1. Знайти  найменший  спільний  знаменник  дробів.
2. Звести  дроби  до  спільного  знаменника.
3. Додати  або  відняти  одержані  дроби.
4. Розкрити  дужки  в  чисельнику.
5. Звести  подібні  доданки  в  чисельнику.
6. Розкласти  чисельник  на  множники,  якщо  це  можливо.
7. Спростити  дріб,  якщо  це  можливо

 

Алгоритм  № 2

(додавання  та  віднімання  дробів )

1. Розкласти  знаменник  кожного  дробу  на  множники.
2. Знайти  найменший  спільний  знаменник.
3. Знайти  додаткові  множники  для  кожного  дробу.
4. Додати  або  відняти  одержані  дроби  з  однаковими  знаменниками.
5. Розкрити  дужки  в  чисельнику.
6. Звести  подібні  доданки  в  чисельнику.
7. Розкласти  чисельник  на  множники,  якщо  це  можливо.
8. Спростити  дріб,  якщо  це  можливо.
9. Приклад  розв’язано.

Алгоритм  №3

(перетворення  цілого  виразу  в  дріб )

1. Якщо  є  цілий  вираз,  то  запишіть  його  як  дріб,  знаменник  якого  рівний  одиниці.
2. Якщо  знаменники  двох  дробів – протилежні  по  знаку  вирази,  то  домножте  чисельник  і  знаменник  одного  із  дробів  на  -1.
3. Розкладіть  знаменник  кожного  дробу  на  множники.
4. Знайдіть  найменший  спільний  знаменник.
5. Знайдіть  додатковий  множник  для  кожного  дробу.
6.    Додайте  або  відніміть  дроби  з  однаковими  знаменниками  і  спростіть  вираз.

7.Розкладіть  чисельник  на  множники,  якщо  це  можливо.

8. Спростіть  дріб,  якщо  це  можливо.

9. Приклад  розв’язано.

 

Алгоритм № 4

( множення  дробів )

1. Перемножте  чисельники  дробів,  цей  вираз  запишіть  у  чисельник  добутку.
2. Перемножте  знаменники  дробів,  цей  вираз  запишіть  в  знаменник  добутку.
3. Спростіть  чисельник  і  знаменник  добутку,  якщо  це  можливо.
4. Якщо  чисельник  або  знаменник  одного  із  дробів  мав  знак  мінус,  то  поставте  знак  мінус  перед  добутком.

 

Алгоритм №5

(ділення  дробів )

1. Перший  дріб  залиште  без  змін.
2. До  другого  запишіть  обернений  ( поміняйте  чисельник  і  знаменник  місцями ).
3. Виконайте  множення  дробів.

 

 

 

 

 

 

Раціональні  рівняння

Алгоритм

1. Перенести  вираз  із  правої  частини  в  ліву  з  протилежним  знаком.
2. Перетворити  вираз  у  дріб.
3. Використати  умову,  що  дріб  дорівнює  нулю.
4. Розв’язати  отримане  рівняння.
5. Перевірити  розв’язок.
6. Записати  відповідь.

 

 

Квадратні  корені

 

Алгоритм №1

( винесення  множника  з-під  знака  кореня )

1. Підкореневий  вираз  розкладіть  на  множники,  серед  яких  є  квадрати  виразів.
2. Застосуйте  теорему  про  корінь  із  добутку.
3. Знайдіть  добуток  одержаних  множників.
4. Запишіть  відповідь

 

Алгоритм № 2

( внесення  множника  під  знак  кореня )

1. Множник  перед   знаком  кореня  піднесіть  до  квадрата.

2  Запишіть  одержаний  квадрат  під  знак  даного  кореня.

3. Знайдіть  добуток  виразів  під  знаком  кореня.

 

 

 

 

9 клас

Нерівності

Алгоритм  № 1

(розв’язування  лінійної  нерівності )

1.Виконайте  тотожні  перетворення.

2.Перенесіть  невідомі  доданки  в  одну  частину  нерівності,  відомі – в  другу , змінивши  знаки  цих  доданків  на  протилежні.

 3. Зведіть  нерівність  до  виду  ax >b , ax <b .

4. Поділіть  обидві  частини  нерівності  на  коефіцієнт  при  змінній . Якщо  коефіцієнт  додатний , то  знак  нерівності  збережіть;  якщо  коефіцієнт  від’ємний , то  знак  нерівності  змініть  на  протилежний.

 5. Зобразіть  розв’язок  нерівності  на  координатній  прямій  у  вигляді  числового  проміжку.

 6. Запишіть  відповідь.

 

Алгоритм  № 2

( розв’язання  систем  лінійних  нерівностей )

1.    Розв’яжіть  кожну  нерівність  системи , користуючись  алгоритмом № 1 .
2.    Зобразіть  на  одній  координатній  прямій  розв’язок  кожної  нерівності .
3.    Виберіть  ті  значення  змінної , які  задовольняють  обидві  нерівності .
4.    Запишіть  відповідь.

 

 

 

 

Алгоритм №3

( доведення  нерівностей )

1. Складіть  різницю  лівої  та  правої  частин  нерівності .

              Виконайте  тотожні  перетворення .

2. Порівняйте  одержаний  результат  з  нулем .
3. Зробіть  висновок .

 

 

Квадратична  функція

Алгоритм

(побудови  графіка  квадратичної  функції )

y = ax²  + bx +c , a ≠ 0.

1  Знаходимо  координати  вершини  параболи  за  формулами

x=-; y=

 

2.Знаходимо  точки  перетину  графіка  функції  з  віссю 

0х , розв’яжемо  рівняння

ax²  + bx +c=0

3.Знаходимо  точку  перетину  графіка  функції  з  віссю  0y :

при  х =0 , y = c .

4.Складаємо  рівняння  прямої , відносно  якої  симетричний  графік  функції : 

x=-

5.Визначте  напрямок « віток « параболи :

при  a > 0  « вітки «  напрямлені  вгору ;

при  a < 0  « вітки «  напрямлені  вниз .