Дидактичний матеріал до теми «Паралельність прямих і площин у просторі»

Дидактичний матеріал до теми «Паралельність прямих і площин у просторі»

Математичний диктант

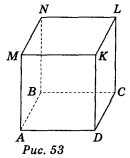
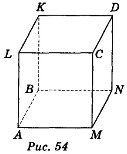
Дано зображення куба: варіант 1 — рис. 53, варіант 2 — рис. 54.

Користуючись зображенням, запишіть:

1. пряму, яка паралельна площині ВСМ і проходить через точку D; (2 бали)
2. грані куба, які паралельні прямій СD; (2 бали)
3. площину, яка містить пряму ВN і паралельна прямій СD; (2 бали)
4. площину, яка паралельна прямій СD і проходить через точку К; (2 бали)
5. площини, які паралельні прямій ВМ; (2 бали)
6. прямі, паралельні площині АВМ. (2 бали)

Самостійна робота

Варіант 1

1) Трикутник АВF і трапеція АВСD (AB || CD) лежать у різних пло­щинах. Доведіть, що пряма СD паралельна площині АВF. (4 бали)

2) Пряма а паралельна площині . Доведіть, що в площині  існує пряма, яка мимобіжна прямій а. (8 балів)

Варіант 2

1) Трикутник АВК і паралелограм АВСD лежать у різних площинах. Доведіть, що пряма СD паралельна площині АВК. (4 бали)

2) Пряма а паралельна площині  . Доведіть, що в площині  існує пряма, яка паралельна прямій а. (8 балів)

Варіант 3

1) Дано куб АВСDА₁B₁С₁D₁. Доведіть, що пряма АС паралельна пло­щині А₁С₁D. (4 бали)

2) Дано мимобіжні прямі а і b. Доведіть, що існує площина, яка міс­тить пряму а і паралельна прямій b. (8 балів)

Варіант 4

1) У трикутній піраміді SАВС точки М. і N —.середини ребер SА і SВ,  відповідно. Доведіть, що пряма МN паралельна площині АВС. (4 бали)

2) Дано паралельні прямі а і b. Доведіть, що існує площина, яка міс­тить пряму а і паралельна прямій b. (8 балів)

Проведення тесту на визначення істинності математичних тверджень.

Вчитель читає твердження, учні ставлять «+», якщо твердження істинне, і «-», якщо воно хибне. Правильність визначення твердження оцінюється 1 балом. У квадратних дужках вказано відповіді.

Тест

1) Якщо  ||  , то будь-яка пряма площини  паралельна площині . [+]

2) Якщо  || , то будь-яка пряма площини  паралельна кожній прямій площини . [-]

3) Якщо  || , то будь-яка пряма площини  мимобіжна кожній прямій площини . [-]

4) Якщо  || , то для будь-якої прямої а площини  існує пряма b в площині  така, що а || b. [+]

5) Якщо  || , то для будь-якої прямої а площини  існує пряма b в площині  така, що прямі а і b — мимобіжні. [+]

6) Якщо  || , то будь-яка пряма, яка перетинає площину , перети­нає і площину  . [+]

7) Якщо  || , то будь-яка пряма, яка паралельна площині , пара­лельна і площині . [-]

8) Якщо дві прямі площини  паралельні відповідно двом прямим площини , то  || . [-]

9) Якщо деяка пряма площини  паралельна площині , то  || . [-]

10) Якщо кожна пряма площини  паралельна площині , то  || . [+]

11) Якщо дві прямі, одна з яких лежить у площині  , а друга — в площині , не мають спільних точок, то  || . [-]

12) Якщо кожні дві прямі, одна з яких лежать у площині , а дру­га — в площині , не мають спільних точок, то  || . [+]

Самостійна робота

Варіант 1

1. Точка О лежить між паралельними площинами α і β. Прямі а і b, які проходять через точку О, перетинають площину а в точках A₁ і B₁, а площину β — в точках А₂ і B₂ відповідно. Знайдіть OB₁, якщо А₁0 : А₁А₂  = 1 : 3, B₁B₂ = 15 см. (6 балів)
2. У кубі ABCDA₁B₁C₁D₁ побудуйте переріз площиною, яка проходить через точки А, В, К, де точка К — середина ребра СС₁. Знайдіть периметр перерізу, якщо ребро куба дорівнює 2 см. (6 балів)

Варіант 2

1. Паралельні площини α і β перетинають сторони кута АВС в точках А₁, С₁ і А₂, С₂ відповідно. Знайдіть ВС₁, якщо А₁В : А₁А₂ = 1:3, ВС₂ = 12 см. (6 балів)
2. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через точки А, В, С₁. Знайдіть периметр перерізу, якщо ребро куба дорівнює 2 см. (6 балів)

Варіант З

1. На паралельних площинах α і β вибрано по парі точок А₁, А₂ і В₁, В₂ відповідно так, що прямі A₁B₁ і А₂В₂ перетинаються в точ­ці О, яка лежить між площинами. Знайдіть ОА₁, якщо А₁В₁ = 6 см, OB₂ : ОА₂ = 3 . (6 балів)
2. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через точки А, М, N, де точки М і N — середини ребер ВВ₁ і DD₁ відповідно. Знайдіть периметр перерізу, якщо ребро куба дорівнює 2 см. (6 балів)

Варіант 4

1. На паралельних площинах α і β вибрано по парі точок А₁, A₂ і В₁, В₂ відповідно так, що прямі А₁В₁ і A₂B₂ перетинаються в точці О, яка не лежить між площинами. Знайдіть ОА₁, якщо А₁В₁ = 6 см, ОВ₁ : ОА₂ = 3. (6 балів)
2. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через точки А, С, М,. де точка М — середина ребра А₁В₁. Знайдіть периметр перерізу, якщо ребро куба дорівнює 2 см. (6 балів)

Контрольна робота з теми «Паралельність прямих і площин у просторі»

Варіант 1

1. Користуючись зображенням куба ABCDA₁В₁C₁D₁ (рис. 113), запи­шіть ребра куба, які паралельні грані ABCD. (3 бали)

2. Сторона АВ трикутника АВС лежить у площині α, а вершина С не лежить в цій площині. Точки М і N — середини сторін АС і ВС від­повідно. Доведіть, що пряма MN паралельна площині α. (3 бали)
3. Дано дві паралельні площини α і β. Точки А і В належать площи­ні α, точки С і D — площині β. Відрізки AD і ВС перетинаються в точці М, АВ = 10 см, BM = 6 см, CM = 12 см. Знайти довжину відрізка CD. (3 бали)

4.Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через точки А, В і D₁. (3 бали)

Варіант 2

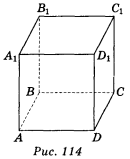
1. Користуючись зображенням куба ABCDA₁B₁C₁D₁ (рис. 114), запишіть грані куба, які паралельні ребру AA₁. (3 бали)

2. Дві сторони даного трикутника паралельні площині α. Доведіть, що і третя його сторона паралельна цій площині. (3 бали)
3. Площина α перетинає сторони АВ і ВС трикутника АВС в точ­ках М і N відповідно і паралельна стороні АС. Знайти довжину від­різка MN, якщо АС = 24 см, а ВМ:АМ = 3:1. (3 бали)
4. Побудуйте переріз куба ABCDA₁B₁C₁D₁ площиною, яка проходить через діагональ ВС₁ грані куба і паралельна діагоналі АС грані куба. (3 бали)