Ділення десяткових дробів.

Тема. Ділення десяткових дробів.

Мета: повторити алгоритми розв'язування задач на знаходження дробу від числа і числа за його дробом (розібраного під час вивчення п. 22) та поширити ці алгоритми на випадки, коли дріб — десятковий; відпрацювати навички розв'язування задач на застосування зазначених алгоритмів.

Тип уроку: засвоєння знань, навичок та вмінь.

Хід уроку

I. Розминка

Усні вправи

1. Виконайте дії:

1) 10,3 + 6,8; 2) 4,3 – 2,6; 3) 4,03 · 0,2; 4) 6,3 : 0,9; 5) 0,8 : 0,4; 6) 0,8 : 0,04;

7) 6 : 0,2; 8) 3 · 0,9; 9) 5,75 : 0,5.

2. Обчисліть значення виразу:

1) 0,03 · 100 + 1,7; 2) 6,8 + 3 : 6; 3) 7,2 : 18 – 0,19 : 19.

3. Михайлик і Петрик зібрали разом 24,8 кг яблук. Михайлик зібрав 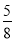усіх яблук. Який з виразів є відповіддю на запитання: скільки яблук зібрав Михайлик?

1) 24,8 : 5 · 8; 2) 24,8 : 8 · 5; 3) 24,8 – ; 4) 24,8 + .

4. Записати десятковий дріб звичайним: 0,5; 0,05; 1,2; 1,07.

II. Перевірка домашнього завдання

Щоб перевірити якість виконання домашнього завдання, учитель бере на перевірку зошити учнів.

III. Повторення і узагальнення знань

 Оскільки загальні правила знаходження дробу від числа і числа за зна­ченням його дробу будуть вивчені лише у 6 класі, на цьому уроці алго­ритм розв'язування названих типів задач є продовженням алгоритму, що був сформований під час вивчення теми «Звичайні дроби».

(Додається лише 1 пункт— запис десяткового дробу звичайним). То­му вчителю достатньо лише розв'язати разом з учнями 2 типові задачі, а потім переходити до самостійного розв'язування учнями задач.

Задача 1. У Василька було 12 грн., 0,3 яких він витратив на нову книж­ку. Скільки гривень заплатив Василько за книжку?

Розв'язання. 1) 0,3 = ;

1) 12 : 10 = 1,2 (грн.) — становить грошей;

2) 1,2 · 3 = 3,6 (грн.) — коштує книжка.

Або скорочено:

1) 0,3 = ;

2) 12 : 10 · 3 = 3,6 (грн.) — коштує книжка.

Відповідь. 3,6 грн.

Задача 2. Турист пройшов 2,7 км, що становить 0,3 туристського мар­шруту. Скільки кілометрів має пройти турист?

Розв'язання. 1) 0,3 = ;

1) 2,7 : 3 = 0,9 (км) — складає маршруту;

2) 0,9 · 10 = 9 (км) — весь маршрут.

Або скорочено:

1) 0,3 = ;

2) 2,7 : 3 · 10 = 9 (км) — весь маршрут.

Відповідь. 9 км.

II. Засвоєння навичок

Оскільки алгоритм, що відпрацьовується, не є новим, на цьому уроці учні можуть розв'язувати як вправи середнього, так і достатнього рівня: №№ 951; 955; 982; 984; 986.

Коментар до розв'язання

№ 951, 955 — розв'язуються за прикладом розібраних задач. Почи­наючи з цього уроку, можна привчати учнів до скороченої форми запису розв'язання.

№951. 1) 0,6 = ;

2) 180 : 10 · 6 = 18 · 6 = 108 (с.) - прочитав Петрик.

Відповідь. 108 сторінок.

№ 982. Щоб «побачити» план розв'язання, можна звернутися до рис. 135. Можна нагадати учням про 2 способи розв'язування подібних задач.

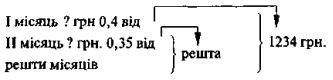
Рис. 135

Розв'язання

1 спосіб

1) 0,4 = ;

1234 : 10 · 4 = 123,4 · 4 = 493,6 (грн.) - за І місяць;

2) 1234 - 493,6 = 740,4 (грн.) - решта;

3) 0,35 = ;

4) 740,4 : 100 · 35 = 259,14 (грн.) - за II місяць.

2 спосіб

1) Уся сума 1;

1 – 0,4 = 0,6 = становить решта;

2) 1234 : 10 · 6 = 740,4 (грн.) - решта;

3) 0,35 = ;

4) 740,4 : 100 · 35 = 259,14 (грн.) — витратили за II місяць.

Відповідь. 259,14 грн.

№ 984. Треба показати учням на можливі 2 способи розв'язання

1 спосіб

1) 0,36 = ; 2,88 : 36 · 100 = 8 - сума;

2) 8 – 2,88 = 5,12 - II доданок.

2 спосіб

1) Уся сума становить 1, тоді якщо І доданок становить 0,36 суми, то другий становить 1 – 0,36 = 0,64 суми;

2) 0,36 = ; 0,64 = ; 2,88 : 36 = 0,08 – становить суми;

3) 0,08 · 64 = 5,12 — другий доданок.

Відповідь. 5,12 — другий доданок.

№ 986. Щоб розібратись в умові, можна записати її у вигляді схеми.

х — шукане число

0,85 від х   –   0,68 від 50

Розв'язання

1) 0,68 = ; 50 : 100 · 68 = 34 становить 0,85 від числа;

2) 0,85 = ; 34 : 85 · 100 = 40 - шукане число.

Відповідь. 40.

V. Підсумок уроку

Запитання до класу

1. Відомо, що число а становить 0,6 від числа b. Чи правильно, що:

1) a = b : 610; 2) а = b : 10 · 6?

2. Якому завданню відповідає рівність?

1) Число встановить 0,6 від числа а.

2) Число 0,6 становить b частин від числа а.

VI. Домашнє завдання

п. 31 №№ 950; 952; 954; 956; 983; 964(3).