Ділення раціональних чисел.

Тема. Ділення раціональних чисел.

Мета: базуючись на знаннях учнів про зміст дії ділення та правил множення раціональних чисел, сформулювати правила ділення раціо­нальних чисел, розпочати роботу з вироблення вмінь застосовувати ці правила для розв'язування вправ, що передбачають виконання ділення раціональних чисел.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Перевірка домашнього завдання

Збираємо зошити на перевірку.

II. Актуалізація опорних знань

Запитання до класу

1. Як називаються числа а, b, с у рівності а · b = с? Як знайти а, якщо b та с відомі?
2. Чому дорівнюють добутки -3 · (-5); 3 · 5; -3 · 5; 3 · (-5)?
3. Як називаються числа a, b, с у запису: a : b = c?

Як перевірити правильність виконання ділення?

4. Замість * поставте такі числа, щоб рівність була правильною:

3,97 · * = 3,97;  · * = 0; 0 · * = 0; 0 · * = 1.

III. Формування знань

 Можна викладення нового матеріалу розбити на два уроки: за ана­логією, як були розглянуті питання додавання та множення раціональних чисел — на першому уроці ми виводили правило ділення двох раціональних чисел з однаковими знаками, на друго­му — ділення чисел з різними знаками. Якщо ж правила множен­ня раціональних чисел опрацьовані учнями на достатньому рівні, можна дати на першому уроці теми правила і властивості ділення раціональних чисел (тобто весь теоретичний матеріал), а другий та третій уроки теми (уроки № 94, 95) повністю присвятити відпрацюванню навичок використання названих вище правил.

1. Зміст ділення раціональних чисел

Завдання 1. Невідоме число помножили на -3, дістали 15. Яке невідоме число?

Розв'язання. Очевидно, що умову задачі мовою математики записують так: якщо х — невідоме число, то x · (-3) = 15; зрозуміло, що x = 15 : (-3).

Отже, поділити якесь а на b означає знайти таке с, щоб a = b · c.

2. Ділення двох чисел з однаковими знаками

Ми знаємо, що -3 · (+5) = -15; -3 · (-5) = + 15, і щоб помножити два числа з однаковими знаками (різними знаками), достатньо перемно­жити їх модулі та перед результатом поставити знак «+» («-»).

Але якщо -3 · (+5) = -15, то -15 : (+5) = -3; -15 : (-3) = +5;

або -15 : (+5) = -(|-15| : |+5|) = -(15 : 5) = -3;

та -15 : (-3) = +(|-15| : |-3|) = +(15 : 3) = +5.

Неважко помітити, що під час ділення раціональних чисел з однако­вими (різними) знаками достатньо поділити модуль діленого на модуль дільника та перед результатом поставити знак «+» («-»).

(Зазвичай спочатку визначають знак частки, а потім вже виконують ділення модулів.)

Наприклад

а)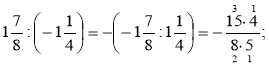

б) -25,116 : (-3,12) = 25,116 : 3,12 = 2511,6 : 312 = 8,05.

 Важливо підкреслити, що є певна аналогія між правилами мно­ження та ділення раціональних чисел (це допоможе учням швид­ше запам'ятати ці правила).

3. Властивості ділення

Ми вже знаємо, що а·1 = а; а · 0 = 0, отже, зі змісту ділення випливає:

а : 1 = а, а : а = 1, 0 : а = 0, якщо а ≠ 0, але а : 0 не можна ні при яких а (якщо в учнів виникнуть запитання «чому?», можна повторити пояснення, якими користувалися під час вивчення теми «Ділення натуральних чи­сел» у 5 класі).

IV. Формування вмінь

Усні вправи

1. Прочитайте рівності, назвіть компоненти дій. Чи правильно вико­нане ділення раціональних чисел?

а) (-36) : (-12) = -3; б) -36 : (+12) = -3; в) (-36) : (-12) = +3; г) -36 : (-12) = +.

2. Який знак має частка?

а) -18 : (-12); б) -99 : 12; в) +40 : (-1).

3. Обчисліть: а) (-40): (-2); б) -125 : 5; в) 0 : (-51); г) 203 : (-10); д) -56 : 14;

є) 80 : (-16); ж) -90 : (-15); з) -25,3 : 0,1.

Письмові вправи

1. Знайдіть частку:

а) - 4,5 : 9; б) - 5 : (- 0,5); в) 38,6 : (- 3,86); г) - 9,6 : (- 4,8); д) - 5,2 : 0,01;

є) - 340 : (- 1,7); ж) - 6,6 : (- 1,1); з) 14: (-0,28); и) - 350 : 1,75.

2. Знайдіть частку:

а) ; б) ; в) ; г) -3 : 1; д) ; є) .

3. Розв'яжіть рівняння: а) -2х = 10; б) -3х = -9; в) 0,2х = -4; г) -1,2х = 3,6;
   д) -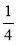х = 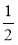; є) -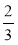х = -1.

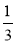Додаткові вправи

1. Спростіть вираз та обчисліть його значення:

а) -5а - 8а + 8a при а = -5; -; -2,6; 1.

б) 7b – 15b + 17b – 10b при b = -1; ; -15,5; 0.

2. Знайдіть значення виразу abc найбільш зручним способом при даних
   значеннях букв:

3. Розв'яжіть рівняння: а) х · (-8,8) = 0; б) (-x) · 3,74 = 0; в) (х – 15) · 5,3 = 0;
   г) (2,3 + x) · (-7,2) = 0; д) -7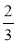 · (х + 9,11) = 0; є) 92,1 · (-89,89 – х) = 0.
4.   а) Яка кількість від'ємних множників повинна бути в добутку, щоб він
   виражався додатним числом? від'ємним числом?

б) За яких умов добуток кількох множників дорівнює 0?

в) Як зміниться добуток кількох чисел, якщо його помножити на (-1)?

V. Підсумки уроку

Запитання до класу

За яким правилом виконуємо ділення двох чисел:

а) з однаковими знаками;

б) з різними знаками;

в) додатного на від'ємне;

г) від'ємного на -3?

VI. Домашнє завдання

Усні вправи

1. Який знак має частка: а) - 18 : (- 12); б) - 99 : 12; в) 40 : (- 32)?
2. Чи правильно виконано ділення?

а) -48 : 6 = -8; б) 0,9 : (-1) = 0,9; в) -4,5 : (- 1,5) = -3?

3. Обчисліть: а) (- 40) : (- 2); б) - 125 : 5; в) 0 : (- 51); г) 203 : (- 10);
   д) - 56 : 14; є) 80: (- 16); ж) - 90 : (- 15); з) - 25,3 : 0,1.

Письмові вправи

1. Знайдіть частку.

а) 3,6: (-4); б) - 2,5 : (-7,5); в) - 8,64 : 1,2; г) - 56,68 : (-0,01);

д) -2 : 0,05; є) -3:; ж) :; з) :; и) :.

2. Розв'яжіть рівняння, а) 4x = -10; б) -0,4х = -2; в) 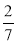х = -.
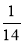3. Знайдіть значення виразу:

а) -5(1,2а – 6) + 7а, якщо a = -208; б) (5а – 0,8) - (-5,2a + 0,1), якщо а = 0,1.