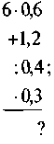Додатні і від'ємні числа. Число 0.

Тема. Додатні і від'ємні числа. Число 0.

Мета:  сформувати уявлення учнів про зміст понять «додатні числа», «від'ємні числа», а також виробити вміння відрізняти ці види чисел і ви­конувати прості вправи, що передбачають таку класифікацію.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Актуалізація опорних знань

Усні вправи

2. На рисунку зображено координатний промінь ОК. Знайдіть координати точок А, В, С, D, Е.

3. На рисунку зображено шкалу термометра, що вимірює температуру повітря. Яку температуру він показує за­ раз? Буде показувати, якщо стовпчик термометра підніметься на 3; на 7 поділок? Буде показувати, якщо стовпчик термометра спуститься на 2; на 5 поділок?

II. Формування знань

 Формуючи уявлення учнів про додатні і від'ємні числа (як і в ба­гатьох інших випадках) важливо спиратися на набутий шести­класниками життєвий досвід. Тому найкращим буде в роботі з но­вим матеріалом спиратися на найпоширеніший об'єкт, що пов'язаний з додатними і від'ємними числами — термометр і знання учнів про вимірювання температури повітря.

Звертаємо увагу на те, що спочатку краще наголосити, що число 0 на термометрі — це значення температури, при якій вода починає перетво­рюватися на кригу, і це число — межа між числами, що позначають більш теплу температуру (додатними), і числами, що позначають більш низьку температуру (від'ємними).

Тому всі числа умовно ділимо на:

а) додатні; б) від'ємні; в) недодатне і невід'ємне, тобто 0.

Запис і читання додатних і від'ємних чисел зазвичай не викликає труднощів у учнів.

Більш складним, але дуже важливим для подальшого вивчення мате­матики, є поняття «невід'ємне число», «недодатне чийло».

III. Закріплення знань. Засвоєння вмінь

Усні вправи

1. Які з чисел: 4; -8; -11; 53; 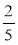; ; 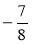0,4; -2,8; +4; + 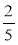додатні? від'ємні?

Які з них рівні між собою?

2. Провідміняйте «додатне число», «від'ємне число», «мінус двісті»,
   «мінус три сьомих».
3. Назвіть за схемою розміщення точок на місцевості порівняно з рівнем
   океану (див. рис).

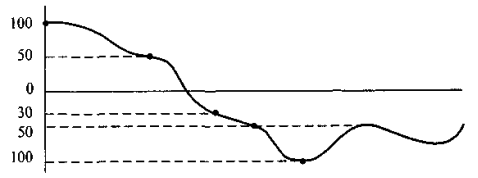
4. Чи правильно, що 0 невід'ємне число? Чи є число 0 недодатним?

Письмові вправи

Задача 1. Намалюйте схематично термометр, який показує -7 °С. Скільки градусів він показуватиме, якщо температура підвищиться на 4 °С? зміниться на 4 °С?

Задача 2. На географічних картах біля гори Говерла і берега Каспійського моря написано числа 2001 і -28. Що вони означають?

Задача 3. Гроші, які вносять до банку, касир записує зі знаком «+», а які бере з банку — зі знаком «-». Як змінилась сума грошей у касі після того, як касир обслужив 5 вкладників? (Див. таблицю)

Задача 4. У школу за рік поступило а учнів, а вибуло b учнів. На скільки змінилась кількість учнів школи за рік? Поясніть зміст відповіді, якщо:

а) а = 40; b = 23; б) а = 37; b = 45; в) а = 53; b = 53.

Задача 5. Чи може виражатися від'ємним числом:

а) кількість людей, що мешкає в будинку;   

б) довжина кімнати;

в) кількість грошей;

г) маса якого-небудь предмета?

Задача 6 (на повторення). Обчисліть значення виразу:

а) ;

б) .

IV. Підсумки уроку

Які слова пропущені?

V. Домашнє завдання

Задача 1. Прочитайте числа: 4,2; -7; -8; 1830; 0; -3,65; 6.  Які з них є: а) від'ємними; б) додатними; в) невід'ємними; г) недодатними?

Задача 2. Іра зайшла в ліфт дванадцятиповерхового будинку на сьомо­му поверсі. Проїхала 4 поверхи і вийшла. На якому поверсі вийшла Іра?

Задача 3. Якщо мале підприємство має на рахунку 5 000 грн, то буде­мо говорити, що воно має + 5 000 грн. Якщо ж підприємство заборгува­ло банку     5 000 грн, то будемо говорити, що воно має — 5 000 грн. Скільки грошей має мале підприємство, якщо воно:

а) має на рахунку 700 грн; 1 500 грн;

б) заборгувало банку 750 грн; 3 000 грн?

Задача (на повторення). Екскурсантів можна посадити в човни або по 4 особи, або по 6 осіб. У кожному разі вільних місць не залишиться. Скільки було екскурсантів, якщо їх більше за 40, але менше від 50?