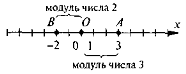
Модуль раціонального числа.
Тема. Модуль раціонального числа.
Мета: сформувати уявлення учнів про геометричний зміст поняття «модуль числа»; виробити вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під знаком модуля.
Тип уроку: засвоєння нових знань і вмінь
Хід уроку
І. Перевірка домашнього завдання
Усні вправи
- Обчисліть
|
а) |
|
б) |
|
|
|
· 17 |
|
· 3 |
|
|
|
|
|
|
|
· 2 |
|
: 3 |
|
|
? |
|
? |
-
Натуральним, цілим чи дробовим числом є -5, 1254567,
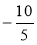 ,
, 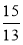 , -3, 5?
, -3, 5?
-
Знайдіть значення виразу -7·(-7), - (+9), - (13), 0, -(-1),
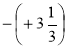 .
.
Під час фронтального виконання усних вправ біля дошки працюють 3 учні, які розв'язують домашні задачі № 2,3 (а, б) (умови вправ записано на дошці заздалегідь)
II. Актуалізація опорних знань
Задача. Знайдіть відстань від початку відліку до точок координатної прямої А(-4), В(4), С(2), Е 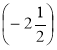 , D(2,5), О(0)
, D(2,5), О(0)
Додаткові завдання
- Чи може шукана відстань бути від'ємним числом, нулем?
- Як пов'язана шукана відстань з координатами точки? Чи може відстань від початку відліку до заданої точки дорівнювати координаті цієї точки?
- Чи зажди відстань від початку відліку до даної точки дорівнює координаті точки? У яких випадках — ні?
II. Формування нових знань
Звичайно, що в 6 класі ще зарано давати строге означення модуля і вводити поняття «геометричний зміст модуля» Але попри все, на інтуїтивному рівні зміст цих понять ми вводимо і вимагаємо від учнів їх засвоєння Поняття модуля в 6 класі якраз вводимо, виходячи з геометричних міркувань, а потім уже на прикладах з'ясовуємо, що:
а) модуль додатного числа є це саме число,
б) модуль нуля є нуль (це ж саме число),
в) модуль від'ємного числа є число, протилежне до даного числа.
Важливо також, виходячи з геометричних міркувань і поняття «протилежні числа», підкреслити, що:
а) модуль даного числа — це єдине число, але,
б) однаковий модуль мають 2 протилежних числа.
У результаті всіх пояснень учителя на дошці і в зошитах можуть бути зроблені записи (конспект 30)
|
|
Конспект 30 |
|
Модуль числа |
|
|
1. Модуль числа а —це відстань від початку координат до точки Л(а) 2. Позначають |-21, |31, \а | 3. Властивості: 1) |0| = 0, 2) | а | = а, якщо а додатне, 3) | а | = -а, якщо а від'ємне, 4) якщо | х | = а, де а — додатне число, то х = а або х = -а |
Приклад
1. 2. | х | = 3, тому х = 3 або х = -3 3. Обчисліть значення виразу:
| 0 | + |
IV. Застосування знань. Формування вмінь
Усні вправи
-
Прочитайте вирази | -8 |,
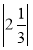 , | 2 + 3 |, | 1,5 – 0,7 |.
, | 2 + 3 |, | 1,5 – 0,7 |.
-
Чи правильна рівність? | 3 | = 3,
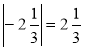 , -| -2 | = -2, | а | = 5.
, -| -2 | = -2, | а | = 5.
- Знайдіть значення виразів, записаних у п. 1.
- Які числа мають модуль, що дорівнює 0; 2; -2?
Письмові вправи
Задача 1. Знайдіть модулі кожного з чисел:
81; 1,3; -5,2; ![]() ;
; ![]() ;
; ![]() ; -52; 0.
; -52; 0.
Запишіть відповідні рівності.
Задача 2. Знайдіть значення виразу |х|, якщо х дорівнює:
а) -12,3; б) -66; в) 83; г) -![]() ; д) 3
; д) 3![]() ; е) -6
; е) -6![]() .
.
Задача 3. Знайдіть відстань (в одиничних відрізках) від початку координат до кожної з точок; А(3,7); В(-7,8); С(-100); D(315,6); E(0); К![]() ; F
; F![]() . Запишіть відповідні рівності.
. Запишіть відповідні рівності.
Задача 4. Знайдіть значення виразу:
а) |-8| - |-5|; б) |-10| · |-15|; в) |240| : |-80|; г) |-7100| + |-290|;
д) |-2,3| + |3,7|; е) |-4,7| - |-1,9|; ж) |28,52| : |-2,3|; з) |0,1| · |-10|;
к) 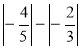 ; л)
; л) 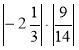 ; м)
; м) 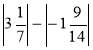 ; н)
; н) 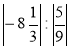 ;
;
о) 3 · |1,5| + 4; п) 24 : |16| + 3,5.
Задача 5. Знайдіть:
а) від'ємне число, модуль якого дорівнює 25; ![]() ; 7,4;
; 7,4;
б) додатне число, модуль якого дорівнює 12; 1; ![]() ; 3,2;
; 3,2;
в) додатні і від'ємні числа, модуль яких дорівнює 8; 5![]() ; 19,2; 0.
; 19,2; 0.
Задача 6. Розв'яжіть рівняння: а) | х | = 6; б) | х | = 8; в) | х | = 0.
Задача 7. Чи існують такі значення х, для яких:
а) х <| х |; б) х >| х |; в) х = | х |?
Задача 8. Ігровий момент.
Учитель. Я задумав два протилежних числа. Поставте тільки одне запитання, щоб дізнатись ці два числа.
V. Підсумки уроку
Запитання до класу
- Що називають модулем числа?
- Як позначають модуль числа?
- Як знайти модуль додатного числа або 0?
- Як знайти модуль від'ємного числа?
- Чи може модуль якого-небудь числа бути від'ємним числом?
- Якими є модулі двох протилежних чисел?
VI. Домашнє завдання
Задача 1. Позначте на координатній прямій числа, модулі яких дорівнюють 3, 8, 1, 35, 5![]() .
.
Задача 2. Обчисліть.
а) 2,5 · |-12| - 5, б) |-8| · |-4| - |-56| : 7, в) 8 + 5 · |-0,7|, г) 13 – 14 · ![]() .
.
Задача 3. Розв’яжіть рівняння а) –у = -8,75, б) -р = ![]() .
.
Задача 4. Площа першого поля становить ![]() площі другого поля Чому дорівнює площа другого поля, якщо площа першою поля 12,6 га?
площі другого поля Чому дорівнює площа другого поля, якщо площа першою поля 12,6 га?


про публікацію авторської розробки
Додати розробку