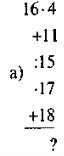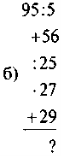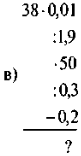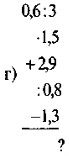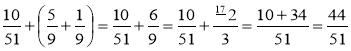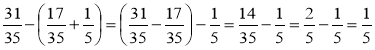Додавання і віднімання дробів з різними знаменниками.
Тема. Додавання і віднімання дробів з різними знаменниками.
Мета: продовжити роботу з формування вмінь застосовувати алгоритми додавання і віднімання дробів з різними знаменниками у більш складних ситуаціях (додавання до 1, а також використання властивостей додавання і віднімання).
Тип уроку: застосування знань і вмінь.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
А. Для перевірки засвоєння знань попереднього уроку запропонувати учням тестові вправи з кодованими відповідями (завдання відповідають базовому рівню знань учнів).
|
Варіант 1 |
Варіант 2 |
|
1. Виконайте додавання |
|
|
а) |
а) |
|
2. Виконайте віднімання |
|
|
а) |
а) |
|
3. Розв'яжіть рівняння |
|
|
а) |
а) |
Б. Фронтально. Усні вправи
- Обчисліть:
|
|
|
|
|
- Знайдіть НСК чисел: 12 і 15; 15 і 30; 12, 15 і 30.
- Перетворіть у звичайний дріб: 0,1; 0,2; 0,25; 0,5; 0,75.
- Обчисліть значення виразу найзручнішим способом:
27 + (13 + 18); 27 – (17 + 8); (27 + 8) – 17.
- Подайте 1 у вигляді дробу зі знаменником: а) 7; б) 10; в) 13.
-
Скоротіть дріб:
 ;
; 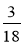 ;
; 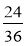 .
.
-
Запишіть мішаним числом:
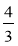 ;
; 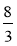 ;
; 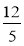 ;
; 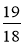 .
.
II. Вдосконалення знань
Якщо алгоритм додавання і віднімання дробів з різними знаменниками засвоєний учнями добре, слід переходити до наступного етапу вивчення теми:
-
віднімання правильних дробів від 1 (пропедевтика цього моменту
була зроблена у 5 класі); -
застосування властивостей додавання і віднімання для обчислень
значень виразів.
Обговорення цих питань можна розпочати з розгляду задач, що приводять до необхідності розв'язування цих вправ. Наприклад.
Задача 1. Першого дня заасфальтували ![]() дороги, другого —
дороги, другого — ![]() , а третього —
, а третього — ![]() дороги. Чи була заасфальтована вся дорога за ці дні?
дороги. Чи була заасфальтована вся дорога за ці дні?
Знайдіть два способи розв'язання задачі.
Під час обговорення і розв'язування задач доходимо до важливих висновків, що можна записати у вигляді конспекту 12.
|
Конспект 12 Властивості додавання і віднімання дробів Якщо а, b, с — дроби, то: 1. a + b = b + a; 2. (a + b) + с = а + (b + с); 3. a – (b + c) = (a – c) – b; 4. (а + b) – c = (a – c) + b. Приклади
1)
2) Доповнення до 1
|
III. Формування і вироблення вмінь
1. Вправи на знаходження доповнення дробу до 1 та додавання і порівняння дробів
-
Знайдіть різницю: а)
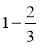 ; б)
; б) 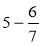 .
.
-
За перший день Ігор прочитав
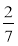 кількості сторінок книжки, за другий —
кількості сторінок книжки, за другий —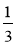 , а за третій — решту. Яку частину книжки прочитав Ігор за третій день?
, а за третій — решту. Яку частину книжки прочитав Ігор за третій день?
-
Магазин продав сувій тканини за три дні. За перший день було продано
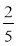 усього сувою, за другий — 36% усього сувою, за третій — решту.
усього сувою, за другий — 36% усього сувою, за третій — решту.
Яку частину тканини продав магазин за третій день?
-
Один кран наповнює ванну за 15 хв, другий — за 12 хв. Яку частину
ванни наповнять крани за 1 хв спільної роботи? -
Один кран наповнює бак за 24 хв, другий — за 36 хв. Чи наповнять крани за 1 хв спільної роботи більше
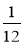 частини бака?
частини бака?
2. Вправи на застосування властивостей додавання і віднімання
- Обчисліть, використовуючи властивості додавання і віднімання:
а) 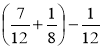 ; б)
; б) 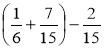 ; в)
; в) 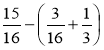 ; г)
; г) 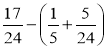 ;
;
д) ![]() ; е)
; е) ![]() .
.
- Через вузьку трубу басейн наповнюється за 10 год, а через широку — за 4 год. Яка труба дає менше води: широка за 3 год чи вузька — за 7 год?
IV. Підсумки уроку
Заповніть клітинки так, щоб рівності були правильними:
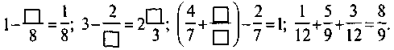
V. Домашнє завдання
-
Знайдіть різницю: а)
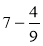 ; б)
; б)  ; в)
; в) 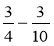 .
.
-
Знайдіть значення виразу: а) 0,9 –
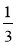 + 0,2; б) 0,4 +
+ 0,2; б) 0,4 + 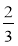 –
–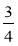 ; в)
; в) 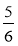 – 0,1 – 0,25.
– 0,1 – 0,25.
-
Довжина прямокутника
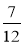 м, а ширина — на
м, а ширина — на 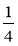 м менша. Знайдіть периметр прямокутника.
м менша. Знайдіть периметр прямокутника.
-
Металеву трубу розрізали на три частини. Довжина першої частини становить
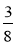 , а другої — 0,3 довжини всієї труби. Який шматок довший — перший чи третій?
, а другої — 0,3 довжини всієї труби. Який шматок довший — перший чи третій?
-
За перший день турист пройшов
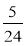 наміченого шляху, за другий —
наміченого шляху, за другий — 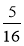 , за третій —
, за третій — 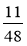 , а за четвертий — решту. Яку частину шляху пройшли туристи за четвертий день?
, а за четвертий — решту. Яку частину шляху пройшли туристи за четвертий день?
Додатково. Обчислити найзручнішим способом:
![]() ;
; 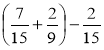 ;
; 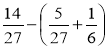 .
.


про публікацію авторської розробки
Додати розробку