Відділ освіти

Новомосковської районної державної адміністрації

Перещепинська загальноосвітня школа І – ІІІ ступенів №1

 

 

 

Науково - дослідницька робота на тему: «Графіки тригонометричних функцій та їх застосування»

 

 

 

 

Виконали: учні 10 – го класу

Анастасян Давид

Мазан Владислав

Томяк Анна

Наукові керівники:

Бєлозьорова Н.В. Дємєнєв М.В.

 

 

 

 

 

 

 

 

 

Перещепине – 2011 рік

Відгук

      Науково - дослідницьку роботу виконали учні 10 – го класу Анастасян Давид, Мазан Владислав та Томяк Анна

Мета цього проекту для учнів – застосування знань тригонометричних  функцій для ситуацій реального життя.

Учні починають з складання списку якнайбільшої кількості коливних процесів, які відбуваються в різних галузях науки і техніки, які зустрічаються у природі і житті.  Потім вони досліджують один із таких прикладів за допомогою програми для побудови графіків Advanced Grapher і комп’ютерної презентації  і обирають проблему,  яка пов’язана з коливними процесами, і яка може бути описана за допомогою тригонометричних функцій.

Потім учні  виконують лабораторну роботу, щоб отримати данні для опрацювання. Учні створюють презентації, публікації, спілкуються один з одним за допомогою сучасних технологій.

На завершення учні обирають ситуацію із реального життя, описують її математично та створюють її у Power Point презентацію, використовуючи тригонометричні функції для опису циклічних процесів.

 

 

 

 

 

 

 

З м і с т :

1.     Історична довідка.

2.     Тригонометричні функції.

2.1. Функція y = sin x, її графік та властивості.

2.2. Функція y = cos x, її графік та властивості.

2.3. Функція y = tg x, її графік та властивості.

2.4. Функція y = ctg x, її графік та властивості.

3.     Трансформація графіків функцій.

3.1.    f (x) ± b.

3.2.    f (x ± b).

3.3.    k f (x).

3.4.    f (kx).

3.5.    |f (x)|.

3.6.    f (|x|).

3.7.    f (-x).

3.8.    – f (x).

4.     Застосування тригонометричних функцій та їх графіків у фізиці.

5. Роль тригонометрії  у нашому житті.
6. Додатки.
7. Використана література та інші джерела.

Анотація

Мета цього проекту для учнів – застосування знань тригонометричних  функцій для ситуацій реального життя.

Учні починають з складання списку якнайбільшої кількості коливних процесів, які відбуваються в різних галузях науки і техніки, які зустрічаються у природі і житті.  Потім вони досліджують один із таких прикладів за допомогою програми для побудови графіків Advanced Grapher і комп’ютерної презентації  і обирають проблему,  яка пов’язана з коливними процесами, і яка може бути описана за допомогою тригонометричних функцій.

Потім учні  виконують лабораторну роботу, щоб отримати данні для опрацювання. Учні створюють презентації, публікації, спілкуються один з одним за допомогою сучасних технологій.

На завершення учні обирають ситуацію із реального життя, описують її математично та створюють її у Power Point презентацію, використовуючи тригонометричні функції для опису циклічних процесів.

 

 

 

 

 

 

 

1.     Історична довідка.

 

     Тригонометрія виникла і розвивалась в давні часи, як один із розділів астрономії. Саме астрономія визначила той факт, що сферична тригонометрія виникла раніше, ніж плоска.

     Деякі тригонометричні відомості були відомі давнім вавилонцям і єгиптянам, але основи цієї науки були закладені в Древній Греції. Древньогрецькі астрономи успішно вирішували деякі питання з тригонометрії, зв’язані з астрономією. Але вони розглядали не лінії синуса, косинуса та ін., а хорди. Роль лінії синусів кута α у них виконувала хорда, яка стягує дугу 2α.

     Грецький астроном Гіппарх в ІІ ст. до н.е. склав таблицю числових значень хорд в залежності від величин стягуваних ними дуг. Більш повні дані з тригонометрії містяться у відомому «Альмагесті» Птолемея.

     Птолемей ділив круг на 360 частин, а діаметр на 120 частин. Він вважав, що радіус складається з 60 частин (60^ч). Кожну з частин він ділив на 60’, а кожну мінуту на 60”, секунду – на 60 терцій (60”’ ). Отже, він користувався шестидесятиричною системою  числення.

    Для прямокутного трикутника з гіпотенузою, яка дорівнює діаметру круга, він записував на основі теореми Піфагора: (хорда α)² + (хорда |180 – α|)² = (діаметру)², в сучасному вигляді це: sin²α + cos²α = 1. Використовуючи уже відомі з геометрії теореми, вчений знайшов багато залежностей, які відомі і зараз.

     Птолемей також склав таблицю синусів від 0^⁰ до 90^⁰ з кроком у 0,25^⁰, яка збереглася до нашого часу.  

     Назви ліній синуса та косинуса вперше були введені індійськими вченими, саме вони склали перші таблиці синусів, хоча менш точні ніж птолемеєві. В Індії и починається вчення про тригонометричні величини, яке назвали гоніометрією.

     Насір ад-Дін Мухамадд ат-Тусі (1201 - 1274) в «Трактаті про повний чотиристоронник» вперше виклав тригонометричні відомості як самостійну частину математики, а не як  додаток до астрономії.

     На порозі XVII ст. в розвитку тригонометрії з’являється новий напрям – аналітичний. Якщо до цього головною метою тригонометрії вважалося вирішування трикутників, обчислення елементів геометричних фігур, і вчення про тригонометричні функції будувалося на геометричній основі, то в XVII – XIX ст. тригонометрія поступово стає однією з глав математичного аналізу. Її широко використовуюсь механіці, фізиці, техніці, особливо при вивченні коливальних рухів та інших періодичних процесів. Про властивість періодичність тригонометричних функції знав ще Вієт, перші математичні дослідження якого відносились до тригонометрії.

     З фізики відомо, що рівняння гармонічного коливання (наприклад, коливання маятника, перемінної електричної напруги) має вигляд:

y = A sin (ωt + α).

     Графіками гармонічних коливань є синусоїди, тому у фізиці и техніці самі гармонічні коливання часто називають синусоїдальними коливаннями.

    Розширення уявлень про тригонометричні функції призвело до обґрунтування їх на новій, аналітичній основі: тригонометричні функції визначаються незалежно від геометрії, за допомогою степеневих рядів  та інших понять математичного аналізу.

     В наш час тригонометрія більше не розглядається як самостійна частина математики. Найважливіша її частина – вчення про тригонометричні функції  - являється частиною більш загального, побудованого з єдиної точки зору вчення про функції, в досліджуваних в математичному аналізі; інша її частина – обчислення трикутників – розглядається як розділ геометрії (плоскої і сферичної)

2. Тригонометричні функції.

2.1 Функція y = sin x, її графік та властивості.

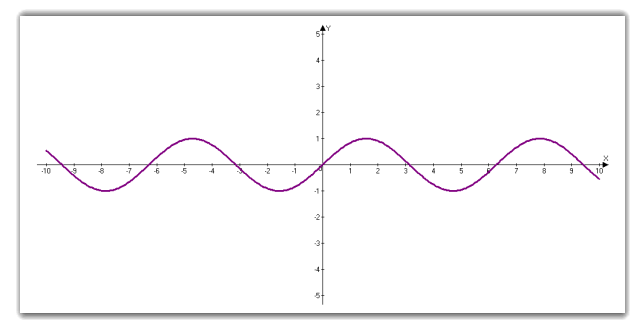Графіком функції  y = sin x є синусоїда

Властивості синусоїди:

Область визначення   R.

Область значень 
Період функції =
Функція непарна, отже .
f (x) = 0, при

Проміжки знакосталості:

sin x   0 на кожному з проміжків виду

sin x   0 на кожному з проміжків виду .

Найбільшого значення, яке дорівнює 1, набуває в точках виду

Найменшого значення, яке дорівнює -1, набуває в точках виду .

Функція зростає на кожному з проміжків

Функція спадає на кожному з проміжків 

2.2  Функція y = cos x, її графік та властивості.

Графіком функції y = cos x є косинусоїда.

Властивості косинусоїди:

 

Область визначення   R.

Область значень .
Період функції = .
Функція парна, отже – cos (-x) = cos x.
f (x) = 0, при .

Проміжки знакосталості:

cos x   0 на кожному з проміжків виду

cos x   0 на кожному з проміжків виду .

Найбільшого значення, яке дорівнює 1, набуває в точках виду

Найменшого значення, яке дорівнює -1,набуває в точках виду

Функція зростає на кожному з проміжків

Функція спадає на кожному з проміжків  .

2.3  Функція y = tg x, її графік та властивості.

 

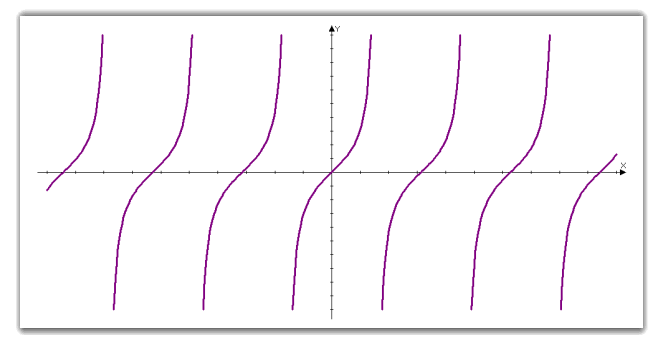Графіком функції y = tg x є тангенсоїда.

Властивості тангенсоїди:

 

Область визначення   R крім чисел виду

Область значень  R.
Період функції = .
Функція непарна, отже – tg (-x) = - tg x.
f (x) = 0, при

Проміжки знакосталості:

tg x   0 на кожному з проміжків виду

tg x   0 на кожному з проміжків виду

Найбільшого значення і найменшого значення не набуває.

Функція зростає на кожному з проміжків

2.4  Функція y = ctg x, її графік та властивості.

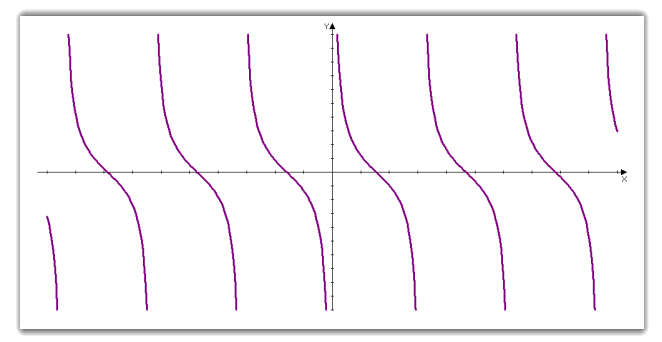Графіком функції y = ctg x є котангенсоїда.

Властивості котангенсоїди:

 

Область визначення   R крім чисел виду

Область значень  R.
Період функції = .
Функція непарна, отже – ctg (-x) = - ctg x.
f (x) = 0, при  

Проміжки знакосталості:

ctg x   0 на кожному з проміжків виду

ctg x   0 на кожному з проміжків виду

Найбільшого значення і найменшого значення не набуває.

Функція спадає на кожному з проміжків

3.  Трансформація графіків функцій.

 

     Трансформація графіків тригонометричних відбувається шляхом їх розтягнення та стиснення, переміщення графіка відносно осей абсцис та ординат та дзеркального відображення відносно осі абсцис.

     Наглядно приводити приклад трансформації цих графіків будемо на зразку косинусоїди.

 

3.1  Графік f (x) ± b.

 

     Графік функції у = f (x) ± b отримаємо з графіку функції у = f(x) паралельним переносом на (b) одиниць по осі ординат.

     Побудуємо графік  у = cos(x) + 2. Бачимо, що графік перемістився на 2 одиниці вгору.

                

 

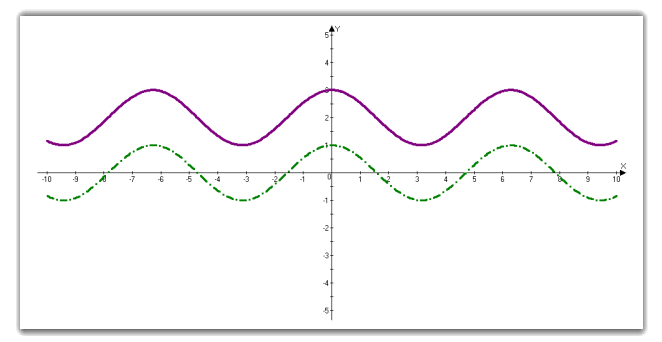
3.2  Графік f (x ± b).

 

     Графік функції  у = f ( x + b ) отримаємо з графіку функції  у = f(x) паралельним переносом на ( -b ) одиниць по осі абсцис.

     Побудуємо графік функції у = cos(x + 2). Бачимо, що графік перемістився на 2 одиниці вліво.

 

 

 

 

 

                               

 

 

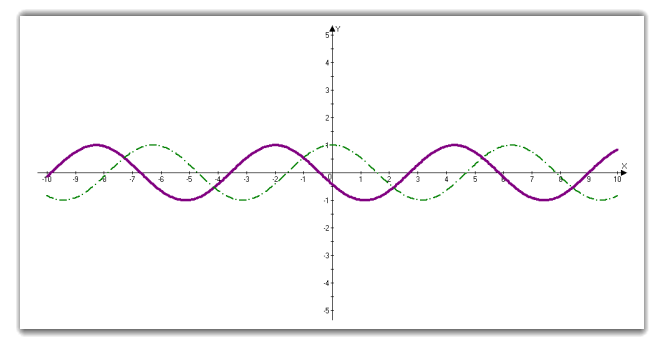
3.3 Графік kf (x).

 

     Графік функції у = k f (x) отримаємо з графіку функції у = f (x) шляхом його розтягу в k раз (при k > 1)  по осі ординат або шляхом його стиснення в k раз (при 0 < k < 1) по осі ординат.

     Побудуємо графіки функцій у = 0,5f (x) та у = 3f (x) та порівняємо їх із стандартною косинусоїдою. Бачимо, що у першому випадку графік стиснувся в 2 рази, а в другому – він розтягнувся відносно осі ординат в 3 рази.

 

 

 

 

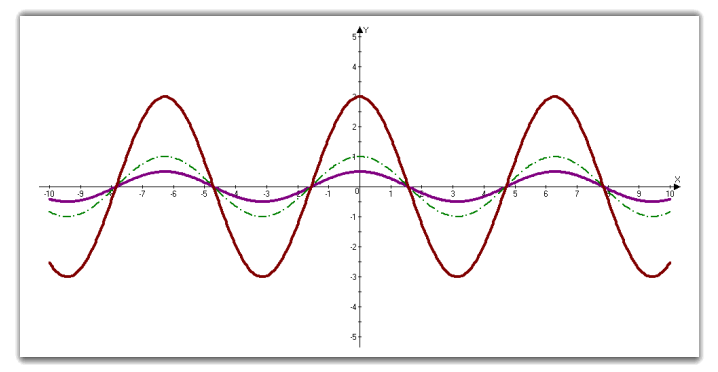
3.4 Графік f (kx).

 

     Графік функції у = f (kx) отримаємо з графіку функції    у = f (x) шляхом його стиснення в k раз (при k > 1)  по осі ординат або його розтягу в k раз (при 0 < k < 1) по осі ординат.

      Побудуємо графіки функцій у = f (0,5 x) та у = f (3x) та порівняємо їх із стандартною косинусоїдою. Бачимо, що у першому випадку графік розтягнувся в 2 рази, а в другому – він стиснувся відносно осі абсцис в 3 рази.

                                    

 

 

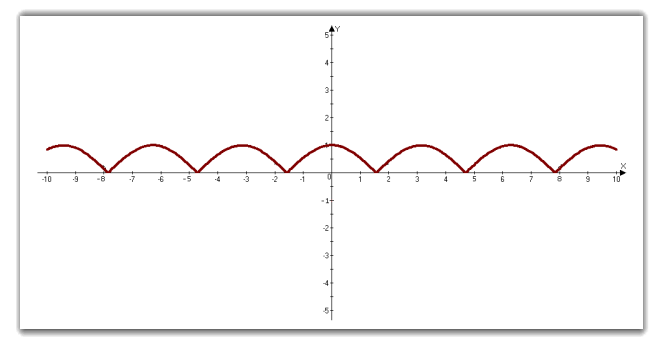
3.5 Графік |f (x)|.

 

Якщо функція має вигляд  у = |f (x)|, то вона не матиме від’ємних значень. Отже всі значення, які  0 дзеркально відображуються відносно осі абсцис.

 

 

 

 

 

 

 

 

 

                                    

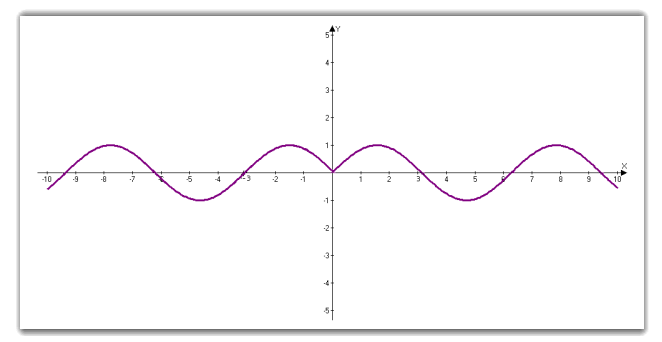
3.6 Графік f (|x|)

 

Так, як cos (x) – парна функція, то її графік залишається без змін, а sin (x) змынюється таким чином:

 

 

 

 

 

 

 

 

                                    

3.7 Графік f (-x)

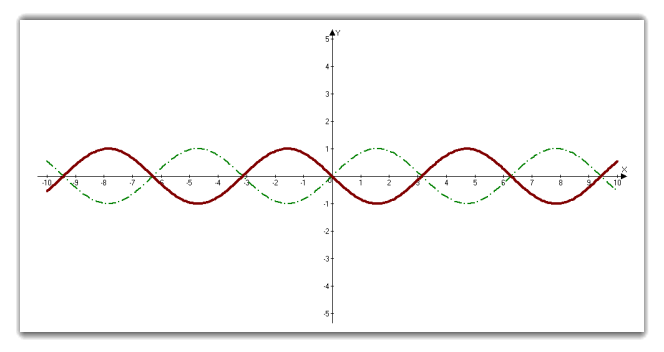sin(-x)

cos(-x) = cos x, так як cos – функція парна. sin (-x) = -sin (x) значить вона непарна. Для побудови графіку sin (-x) потрібно відобразити графік відносно осі ОХ.

 

 

 

 

 

 

 

 

                                 

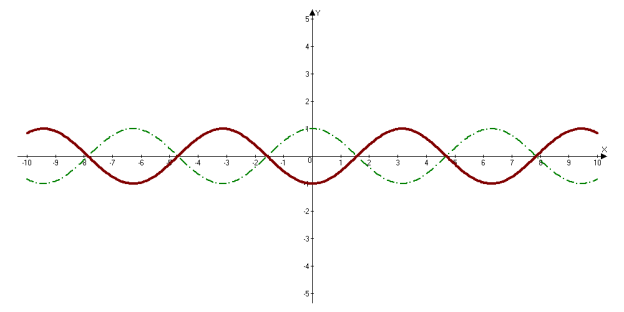
3.8 Графік f -(x)

-cos(x)

Для побудови графіку cos (-x) потрібно відобразити графік відносно осі ОХ.

 

 

 

 

 

 

 

 

 

 

 

4. Застосування тригонометричних функцій та їх графіків у фізиці.

Приклади і означення гармонічних коливань.

      За допомогою тригонометричних функцій математично описують різноманітні коливні процеси, які зустрічаються в фізиці і техніці. Корисно навести учням різні приклади коливних процесів.

     Приклад 1. До кульки масою m прикріплено дві горизонтальні пружини, кінці яких закріплено. Якщо відхилити кульку від положення рівноваги, і знехтувати опором, то рух кульки навколо положення рівноваги буде коливальним.

     Приклад 2. Припустимо, що тягарець масою m підвішено на нитці довжиною l, що не розтягується. Якщо нитку відхилити на деякий кут від положення рівноваги, то система почне коливатися. Це модель так званого математичного маятника.

     Коливальними є також: рух маятника в годинниковому механізмі, рух струни і рух повітря, який вона зумовлює, процес зміни струму в електричній мережі та ін.

     Найпростішими ссеред коливальних рухів є так звані гармонічні коливання, приклади яких наведено вище.

Графіки гармонічних коливань.

     Під час побудови графіків гармонічних коливань доводиться виконувати перетворення графіка синусоїди. Ці перетворення полягають у паралельному перенесенні графіка функції  f(x) = sin x вздовж осі Ох і Оу. Отже, під час побудови графіків гармонічних коливань у фізиці вперше розглядаються загальні способи перетворення графіків.

     Приклад 1. y = Asin x.

     Розв’язання. Тут частота ω = 1, початкова фаза φ = 0, а період збігається з періодом функції y = sin x, тобто дорівнює 2.

     Графік функції y = Asin x відрізняється від графіка функції у = sin x лише амплітудою. Він стиснений до осі Ох при А  1 або розтягнутий від осі Ох при А  0 у відношенні 1 : А.

     У загальному випадку графік функції g(x) = kf(x) дістаємо з графіку функції х f(x), стискуючи чи розтягуючи його від осі Ох у відношенні 1 : k.

    

 

 

 

 

 

 

 

 

5. Роль тригонометрії  у нашому житті.

 

Застосування тригонометрії в повсякденному житті

 

Тригонометрія допомагає нашому мозку визначати відстані до об'єктів.           

Американські вчені стверджують, що мозок оцінює відстань до об'єктів, вимірюючи кут між площиною землі і площиною зору. Такий висновок був зроблений після серії експериментів, учасникам яких пропонувалося поглянути на навколишній світ через призми, що збільшують цей кут. 

Таке спотворення призводило до того, що піддослідні носії призм сприймали віддалені об'єкти як більш близькі і не могли впоратися з найпростішими тестами. Деякі з учасників експериментів навіть нахилялися вперед, прагнучи вирівняти своє тіло перпендикулярно неправильно представляється поверхні землі. Проте після 20 хвилин вони звикли до спотвореного сприйняття, і всі проблеми зникли. Ця обставина вказує на гнучкість механізму, за допомогою якого мозок пристосовує зорову систему до мінливих зовнішніх умов. Цікаво зауважити, що після того, як призми були зняті, деякий час спостерігався зворотний ефект - переоцінка відстані.

Взагалі, ідея "виміру кутів" не є новою. Ще художники Стародавнього Китаю малювали віддалені об'єкти вище в полі зору, трохи нехтуючи законами перспективи. Сформулював теорію визначення відстані за оцінкою кутів арабський учений XI століття Альхазен. Після довгого забуття в середині минулого століття ідею реанімував психолог Джеймс Гібсон (James Gibson), який будував свої висновки на основі досвіду роботи з пілотами військової авіації. Однак після того про теорію знову забули. 

Результати нового дослідження, як можна припустити, виявляться небезінтересні інженерам, що конструюють системи навігації для роботів, а також фахівцям, які працюють над створенням максимально реалістичних віртуальних моделей.Можливі й застосування в області медицини, при реабілітації пацієнтів з пошкодженнями певних областей мозку.

 

Застосування тригонометрії в мистецтві і архітектурі 
 

     З того часу як людина стала існувати на землі, основою поліпшення побуту та інших сфер життя стала наука. Основи всього, що створено людиною - це різні напрямки в природничих і математичних науках. Одна з них - геометрія. Архітектура не єдина сфера науки, в якій використовуються тригонометричні формули. Більшість композиційних рішень і побудов малюнків проходило саме з допомогою геометрії.Але теоретичні дані мало що значать. Хочу навести приклад на побудову однієї скульптури французького майстра Золотого століття мистецтва. 
Пропорційне співвідношення в побудові статуї було ідеально. Однак при піднятті статуї на високий п'єдестал, вона виглядала потворною. Скульптором не було враховано, що в перспективі до горизонту зменшуються багато деталей і при погляді знизу вгору вже не створюється враження її ідеальності. Велося безліч розрахунків, щоб фігура з великої висоти виглядала пропорційно. В основному вони були засновані на методі візування, тобто приблизного вимірювання, на око. Однак коефіцієнт різниці тих чи інших пропорцій дозволили зробити фігуру більш наближеною до ідеалу. Таким чином, знаючи приблизну відстань від статуї до точки зору, а саме від верху статуї до очей людини і висоту статуї, можна розрахувати синус кута падіння погляду за допомогою таблиці (теж саме ми можемо зробити і з нижньою точкою зору), тим самим знайдемо точку зору (рис.1) 
На рис.2 ситуація змінюється, так як статую піднімають на висоту АС і НС збільшуються, можна розрахувати значення косинуса кута С, за таблицею знайдемо кут падіння погляду дорівнює 1.  + sin 2 .У процесі можна розрахувати АН, а також синус кута С, що дозволить перевірити результати за допомогою основного тригонометричного тотожності cos 2.  
Порівнявши вимірювання АН в першому і в другому випадку можна знайти коефіцієнт пропорційності. Згодом ми отримаємо креслення, а потім скульптуру, при піднятті якої візуально фігура буде наближена до ідеалу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновки:

Таким чином, ми застосували знання про тригонометричні  функції для ситуацій реального життя.

Наша група склала список деяких коливних процесів, які відбуваються в різних галузях науки і техніки та зустрічаються у природі і житті.  Ми дослідили один із таких прикладів за допомогою програми для побудови графіків Advanced Grapher і комп’ютерної презентації  та обрали проблему, яка пов’язана з коливними процесами і може бути описана за допомогою тригонометричних функцій.

За допомогою  лабораторної  роботи ми  отримати дані для опрацювання. І тільки потім створили презентацію та публікацію для наочного відображення всієї інформації, яку ми здобули в ході виконання роботи.

В кінці ми обирали ситуацію із реального життя, описали її математично та створили її у PowerPoint презентацію, використовуючи тригонометричні функції для опису циклічних процесів.

 

 

 

 

 

 

 

 

 

 

 

6. Додатки.

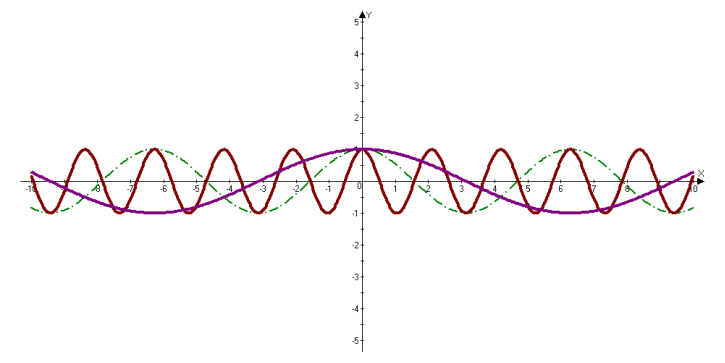
Побудова графіків тригонометричних функцій, які виходять за межі шкільної програми.

 

 

 

 

 

 

 

 

 

 

 

 

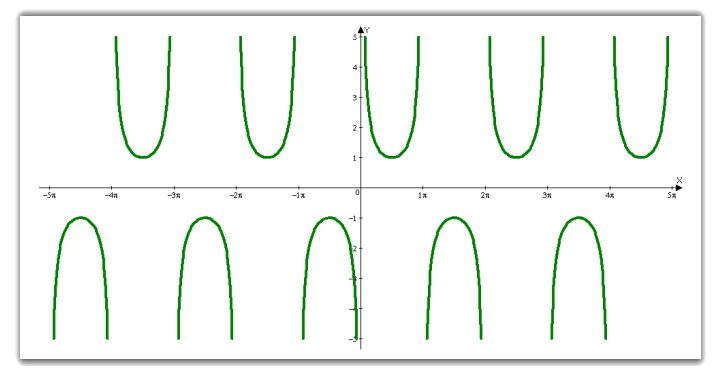
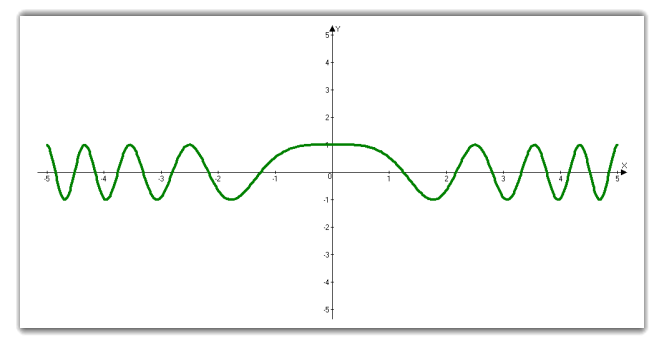
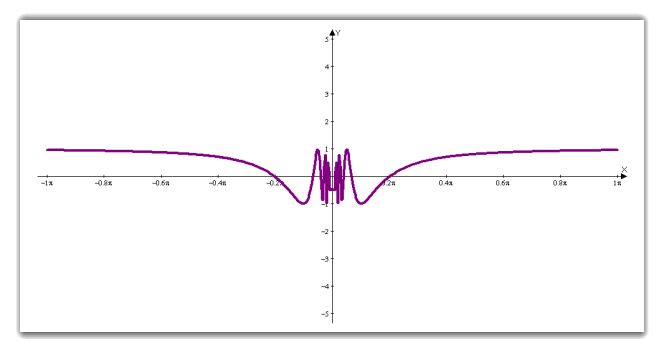
Висновки:

Загалом ми застосували знання про тригонометричні  функції для ситуацій реального життя.

Ми склали список деяких коливних процесів, які відбуваються в різних галузях науки і техніки, які зустрічаються у природі і житті.  Ми дослідили один із таких прикладів за допомогою програми для побудови графіків Advanced Grapher і комп’ютерної презентації  і обрали проблему, яка пов’язана з коливними процесами, і яка може бути описана за допомогою тригонометричних функцій.

Такиж ми виконали лабораторну роботу, для того, щоб отримати данні для опрацювання. Ми створили презентацію, публікацію, для наочного відображення всієї інформації яку ми здобули в ході виконання роботи.

В кінці ми обирали ситуацію із реального життя, описали її математично та створили її у PowerPoint презентацію, використовуючи тригонометричні функції для опису циклічних процесів.

 

 

 

Список використаної літератури:

1. М. І. Жалдак   Комп'ютер на уроках математики. Київ, 1997.
2. «Intel^® навчання для майбутнього».
3. Т. Букарева, В. Келісіді, Проведення практичних занять з математики: практичний посібник, - Дніпропетровськ: Дніпроп. обл.. ін-т післядипломної освіти, 2005, -124с.
4. Підручна Марія, Янченко Галина. Позакласна робота з математики. 10  класи. – Тернопіль: Підручники і посібники, 2001. – 96 с.
5. Шкіль М.І. та ін.. Алгебра і початки аналізу: Підручник для 10 кл. загальноосвітніх навчальних закладів.- К.: Зодіак – ЕКО, 2002.-384 с.
6. Г.И.Глейзер.  История математики в школе. ІХ-Х кл. Издательство «Просвещение». 1983.-350с.
7. Литвиненко Г.М.,Бурда М.І., Собко М.С.. Посібник для тестової перевірки. Математики . «Дніпро», 1993 р.
8. Сборник задач по математике для поступающих в вузы: Учеб. пособие/ Дыбов П.Т., Забоев А.И., Иванов А.С. и др.; под ред. А.И.Прилепко.-М.: Высшая школа, 1983.-239 с., ил.