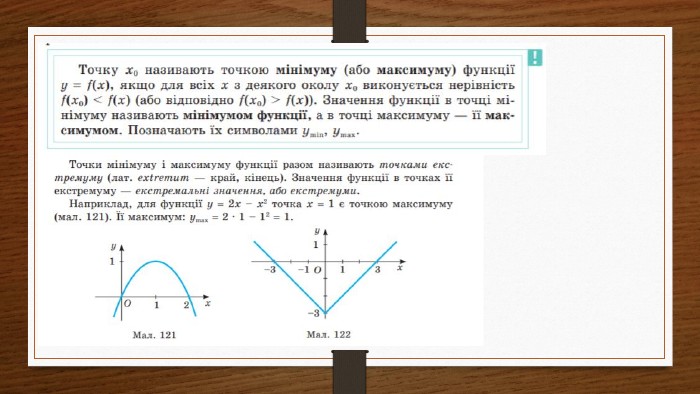
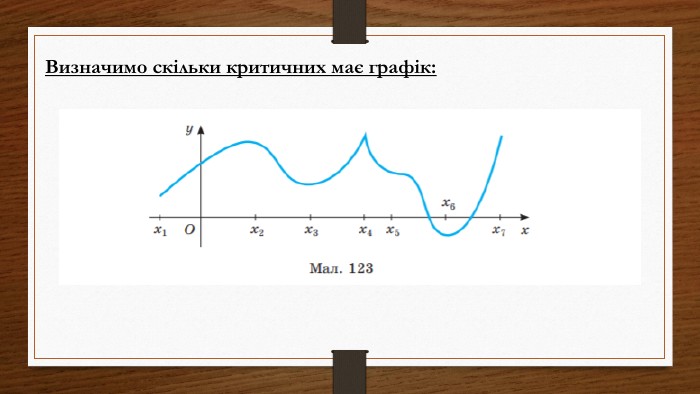
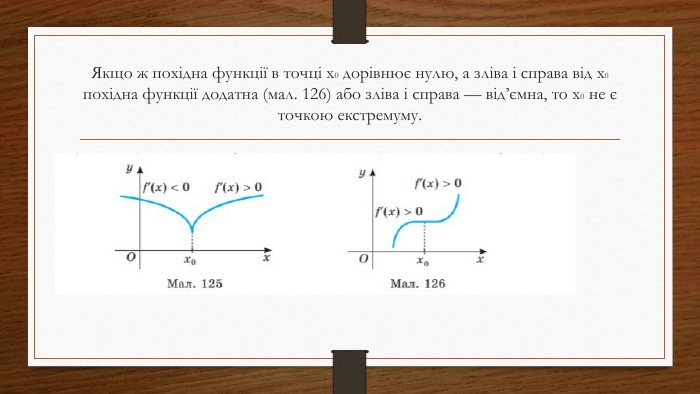
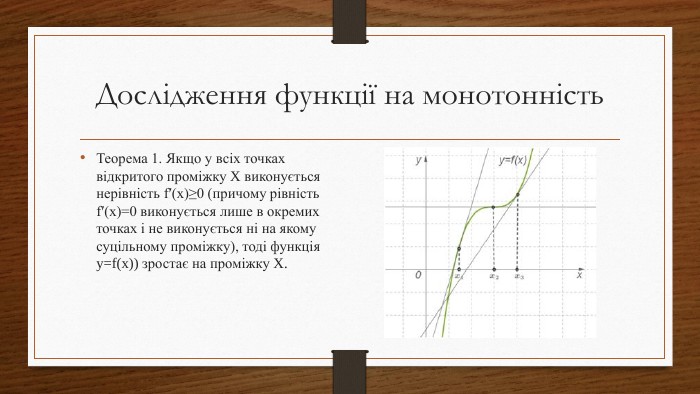
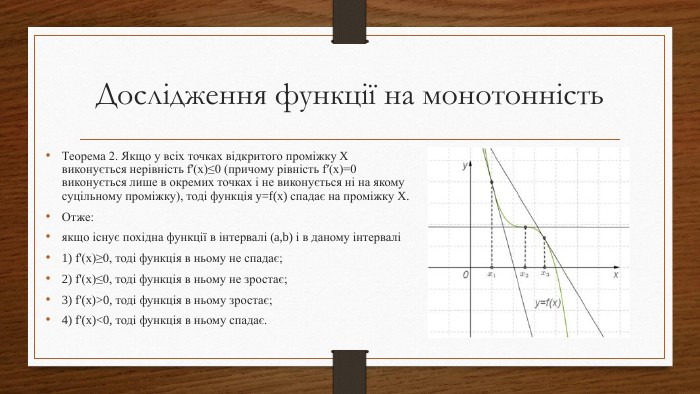
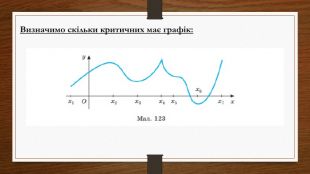
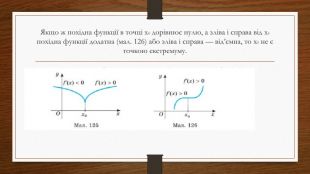
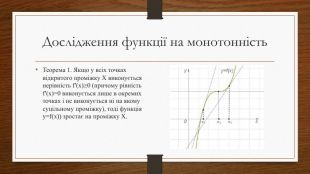
Дослідження функцій на екстремум та монотонність
Про матеріал
Презентація з теми "Дослідження функцій на екстремум та монотонність."(теоретичний матріал, без розв'язаних прикладів) Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку