Урок 1

Тема уроку. Двогранний кут. Лінійний кут двогранного кута.

Мета уроку: формування понять двогранний кут, ребро і грані двогранного кута, лінійний кут двогранного кута, умінь учнів будувати (знаходити) лінійний кут двогранного кута.

Обладнання: стереометричний набір, моделі многогранників.

І. Сприйняття та усвідомлення нового матеріалу

Поняття двогранного кута та його елементів, лінійного кута двогранного кута

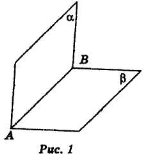
Двогранним кутом називається фігура, утворена двома півплощинами із спільною прямою, що їх обмежує. Півплощини називаються гранями, а пряма, що їх обмежує – ребром двогранного кута.

На рис. 1 зображено двогранний кут з ребром АВ та гранями α і β.

Виконання вправ

1. За допомогою стереометричного набору змоделюйте двогранний кут.
2. Покажіть на моделях многогранників та з оточення двогранні кути, вкажіть їх елементи (ребра, грані).

Лінійним кутом двогранного кута називається кут, утворений в результаті перетину двогранного кута з площиною, яка перпендикулярна до ребра двогранного кута.

На рис. 2 площина γс, φ – лінійний кут двогранного кута.

Мірою двогранного кута називається міра відповідного йому лінійного кута.

Для даного двогранного кута можна побудувати безліч лінійних кутів, проте всі лінійні кути двогранного кута суміщаються в результаті паралельного перенесення, а отже, вони рівні. Тому міра двогранного кута не залежить від вибору лінійного кута.

Якщо φ – лінійний кут двогранного кута, то 0º φ 180º.

Розв’язування  задач

1. Кут між двома площинами 45º. Знайдіть градусні міри двогранних кутів, утворених перетином цих площин. (Відповідь. 45º і 135º.)
2. Двогранний кут має 120º. Чому дорівнює кут між площинами граней цього кута? (Відповідь. 60º.)
3. У трикутнику АСВ <АСВ = 90º (рис. 3), РВ 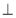(АВС). Доведіть, що <РВС – лінійний кут двогранного кута з ребром АС.
4. РВ(АВС), АВ = ВС, AD = CD (рис. 4). Доведіть, що <PDB – лінійний кут двогранного кута з ребром АС.
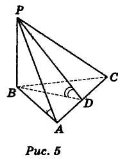
5. Які з відзначений кутів є лінійним кутом двогранного кута з ребром АС, якщо:

а) точка D – середина АС, АВС – правильний, РВ(АВС) (рис. 5);

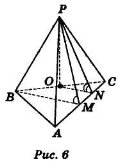
б) точка М – середина АС (рис. 6), ON║ВМ,  АВС – правильний, РО(АВС)?

Способи побудови лінійного кута двогранного кута

Доцільно розглянути наступні задачі на доведення.

Задача 1

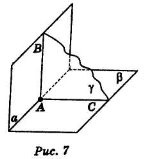
На ребрі двогранного кута вибрана точка і через неї в гранях двогранного кута проведено два промені, перпендикулярні до ребра. Доведіть, що кут утворений  цими променями, буде лінійним кутом двогранного кута.

Розв’язання

Нехай на ребрі двогранного кута вибрано точку А, Аα (рис. 7) і проведено промені АС і АВ, АВα, АСβ, АВα, АСа. Промені АВ і АС визначають площину γ, яка буде перпендикулярна до ребра а (згідно з ознакою перпендикулярності прямої і площини), тому <ВАС – лінійний кут двогранного кута з ребром  а і гранями α і β.

Задача 2

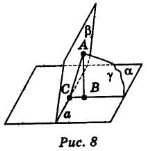В одній із граней двогранного кута вибрано точку А і з неї опущено перпендикуляр АВ до площини другої грані і перпендикуляр АС на ребро кута. Доведіть, що кут АСВ (або суміжний з ним) буде лінійним кутом двогранного кута.

Розв’язання

Враховуючи, що АВα (рис. 8), АСа, то, згідно з теоремою про три перпендикуляри, ВСа.

Оскільки АСа, ВСа, то площина γ, яка визначається прямими АС і ВС, які перетинаються, буде перпендикулярна до ребра а двогранного кута, і тому <АСВ (або суміжний з ним) буде лінійним кутом двогранного кута з ребром а та гранями α і β.

Задача 3*

Через точку провели перпендикуляри до граней гострого двогранного кута. Доведіть, що гострий кут між ними дорівнює лінійному куту двогранного кута.

Розв’язання

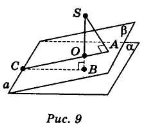
Нехай дано двогранний кут з ребром а і гранями α і β (рис. 9). Проведемо через точку S SBα, SAβ. Прямі SA і SB визначають площину, яка буде перпендикулярна як до площини α, так і до площини β, тобто ця площина буде перпендикулярна до а, і кут АСВ буде лінійним кутом даного двогранного кута.

SOAСОВ (оскільки <СОВ = <SOA – як вертикальні,

<СВО = <SAО = = 90º); отже,  <ОSA = <OCA.

Задача 4*

Доведіть, що синус кута, утвореного прямою, яка лежить у площині однієї із граней двогранного кута, з іншою гранню, дорівнює добутку синуса двогранного кута на синус кута, який утворює дана пряма з ребром двогранного кута (теорема про три синуси).

Розв’язання

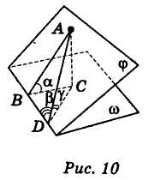
Нехай дано двогранний кут із гранями φ і ω, АСω, <ABC = α – лінійний кут, <ADC = γ, <ADB = β (рис. 10). Доведемо, що sinγ = sinαsinβ. Нехай AD = x,  тоді ΔADB AB = xsinβ; із ΔABC AC = ABsinα = xsinβsinα; із ΔADC

.

Отже, маємо: sinγ = sinαsinβ.

Побудова та знаходження лінійного кута двогранного кута

Розв’язування задач

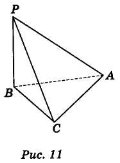
1. Побудуйте лінійний кут двогранного кута з ребром АС, якщо:

а) АВ = ВС, РВ(АВС) (рис. 11);

б) ΔАВС – правильний, точка О – точка перетину медіан, РО(АВС) (рис. 12);

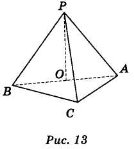
в) ΔАВС —правильний, ВО = ОА, РО (АВС) (рис. 13).

2. На грані двогранного кута, величина якого α , дано точку, яка від­далена від ребра на відстань а. Знайдіть відстань від цієї точки до другої грані. (Відповідь. α sinα.)
3. Точка А належить одній із граней двогранного кута, а її відстань від дру­гої грані дорівнює 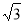см. Знайдіть величину двогранного кута, якщо від­стань від точки А до його ребра дорівнює 2 см. (Відповідь. 60°.)
4. Знайдіть величину двогранного кута, якщо точка, взята на одній із граней, знаходиться від ребра вдвічі далі, ніж від другої грані. (Від­повідь. 30°.)
5. Знайдіть величину двогранного кута, якщо точка, взята на одній із граней, знаходиться від ребра втричі, далі, ніж від другої грані.               

(Відповідь. arcsin.)

6. Точка А знаходиться від граней прямого двогранного кута на від­станях а і b. Знайдіть відстань від точки А до ребра двогранного кута.

(Відповідь. .)

7. На гранях двогранного кута взято дві точки, які знаходяться від його ребра на відстанях а і b. Перша з них знаходиться від другої Грані на відстані с. Знайдіть відстань від другої точки до протилежної грані. (Відповідь. .)
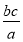8. Дано два двогранні кути, у яких одна грань спільна, а дві інші грані є різними півплощинами однієї площини. Доведіть, що сума цих двогранних кутів дорівнює 180°.
9. Двогранний кут дорівнює α. Із точки С на його ребрі у гранях кута проведено перпендикулярні до ребра відрізки СА і СВ, причому СА = а і СВ = b. Знайдіть відстань від точки А до точки В.

(Відпо­відь. .)

10. Задача № 1 (1) із підручника (с. 76)^[1].
11. Точка М знаходиться всередині двогранного кута на відстанях а і b від його граней. Знайдіть відстань від точки М до ребра двогранного кута, якщо його величина дорівнює α . (Відповідь. )

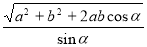II. Домашнє завдання

§ 5, π. 37; контрольні запитання. № 1-3; задача № 1 (2) (с. 76)¹.

III. Підведення підсумку уроку

Запитання до класу

1) Що таке двогранний кут (грань кута, ребро кута)?

2) Дайте означення лінійного кута двогранного кута.

3) Чому міра двогранного кута не залежить від вибору лінійного кута?

4) Які прийоми побудови лінійного кута двогранного кута вам відомі?

5) Чому дорівнює в кубі АВСDA₁В₁С₁D₁ двогранний кут, утворений:

а) основою ABCD і перерізом A₁B₁СD·,

б) гранню CC₁D₁D і перерізом ΑΑ₁C₁C ? (Відповідь, а) 45°; б) 45°.)

^[1] Тут і далі всі посилання зроблено на підручник: Погорєлов О. В. Геометрія: Стереометрія; Підруч. для 10—11 кл. серед, шк. — К.: Освіта, 2001.