елементи комбінаторики

Елементи комбінаторики ( урок по технології « перевернутий урок») Підготувала студентка 41 МЕІ Уманець М.Є. Число, положення і комбінація – три різні сфери думки, але які взаємно перетинаються і до них можна віднести усі математичні ідеї Англійський математик Дж. Сильвестр

Передурочний домашній дослідницький етап Дослідження історичних даних Дослідження основних законів комбінаторики та розв’язування задач з даної теми Прикладне використання комбінаторики Оформлення міні-конспекту по результату дослідження, проведеного за допомогою презентації і інтернет-ресурсів на які були посилання в презентації

«Теорія без практики мертва та безплідна, практика без теорії неможлива чи згубна. Для теорії потрібні головним чином знання, для практики, крім того, і вміння». О.М.Крилов Чи згідні ви з висловленням О.Крилова?

Оскільки «….практика без теорії неможлива чи згубна. Для теорії потрібні головним чином знання….», то перевіримо отримані вами, під час виконання домашнього завдання, знання теоретичного матеріалу по досить цікавій темі і набуті елементарні вміння дослідницьким шляхом

Доповнити речення словами 1. Різні групи елементів деякої множини, що відрізняються елементами або порядком цих елементів, називають ……… 2. Комбінаторика – це розділ математики, в якому вивчаються……….. сполуками. властивості сполук і формули обчислення кількості різних сполук.

Доповнити речення словами 3. Якщо порядком елементів сполуки між собою не відрізняються, то це - ………… 4. Якщо сполуки відрізняються порядком елементів і всі елементи множини входять у сполуку, то це - … …… комбінації перестановки.

Доповнити речення словами 5. Якщо сполуки відрізняються і елементами, і порядком цих елементів, але не всі елементи множини входять у сполуку, то це - ……………… 6. n! = розміщення

Доповнити речення словами m n m n розміщень. перестановок. комбінацій.

Доповнити речення словами 10. Якщо елемент A можна обрати m способами, а елемент В – n способами, то А і В можна обрати ……….. способами. Це правило …………. добутку

11. Якщо елемент А можна обрати m способами, а елемент В – n способами, то А або В можна обрати ………….. способами. Це правило ……………….. Доповнити речення словами (m+n) суми

Вибір формули Чи враховується порядок розміщення елементів Чи всі елементи входять у сполуку? Розміщення An m = n! (n-m)! An m = n(n-1)…(n-m+1) Комбінації Cn m = n! (n-m)!m! Cn m = Перестановки Pn = n! так так ні ні

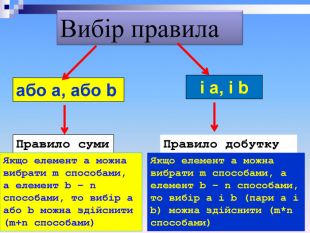
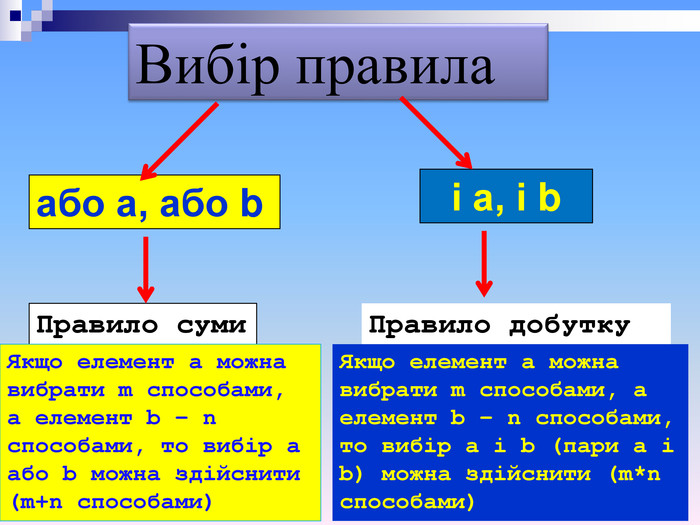
Вибір правила або а, або b і а, і b Правило суми Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а або b можна здійснити (m+n способами) Правило добутку Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір а і b (пари а і b) можна здійснити (m*n способами)

Оскільки «Теорія без практики мертва та безплідна…..», то пропоную вам перейти до практичного застосування отриманих знань

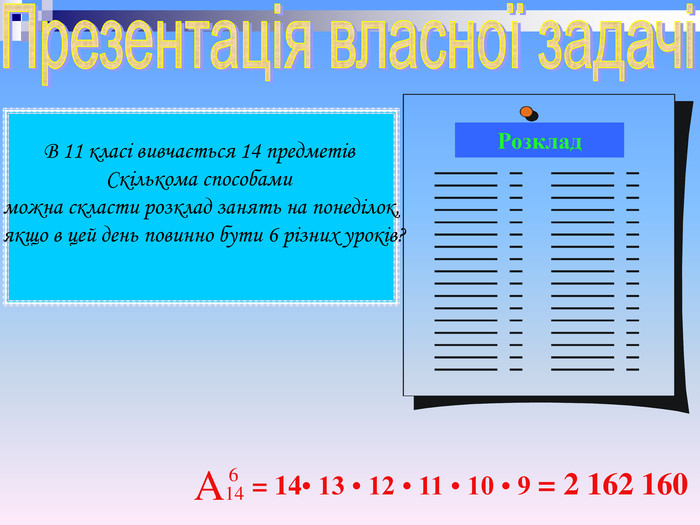
Перед уроком ви розділилися на три групи ( перестановки, розміщення, комбінації). У вас на карточках є ряд задач. Вам необхідно: вибрати з них ті, які розв'язуються відповідно за формулою тієї сполуки, яку ви представляєте; по дві задачі захистити з розв'язком( перед тим нагадавши ще раз основні теоретичні відомості); по 2-3 запропонувати для розв'язку дітям класу; запропонувати власну задач практичного змісту.

I група Перестановки

Число перестановок з n елементів позначається Pn Формула Pn = n! n! = 1 • 2 • 3 … (n -1) • n Характеристичні ознаки предмети різні всі місця зайняті порядок елементів важливий

У школі 20 класів і 20 класних керівників.Скількома способами можна розподілити класне керівництво між учителями? Розв’язання. Кількість можливих розподілів класного керівництва між учителями – це кількість перестановок з 20 елементів. Отже, шукана кількість розподілів дорівнює Р20 = 20!

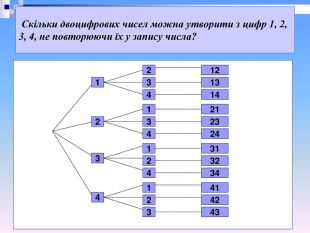
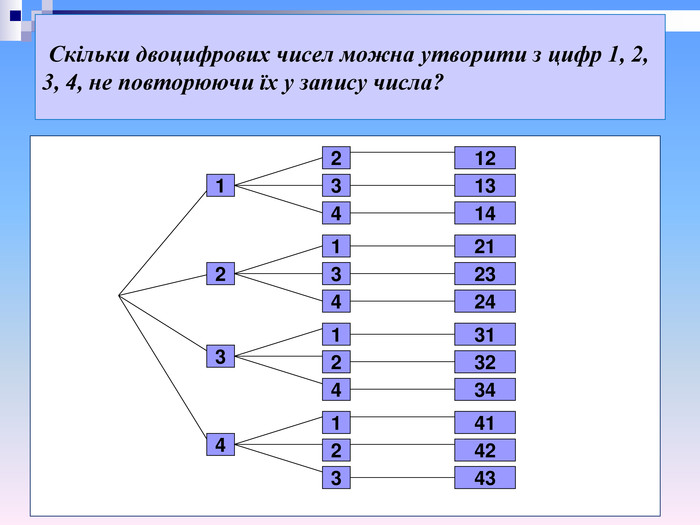
Скільки різних чотирицифрових чисел можна скласти з цифр 0; 1; 2; 3, якщо в кожному числі жодна з цифр не повторюється? Розв’язання. З чотирьох цифр 0; 1; 2; 3 можна утворити Р4 перестановок. Але ті перестановки, які починаються з 0 не будуть записами чотирицифрових чисел, таких перестановок — Р3. Отже, шукана кількість чотирицифрових чисел дорівнює Р4 - Р3 = 4! - 3! = 3!(4 - 1) = 6 ∙ 3 = 18.

У класі навчається 10 юнаків. Скількома способами можна їх вишикувати у шеренгу? Р10 = 10! Скількома способами можна скласти список із 9 прізвищ? Скільки різних п’ятицифрових чисел можна утворити із цифр 3, 5, 7, 8, 9 так, щоб жодна із цифр не повторювалася ? Р9 = 9! Задачі для перевірки розуміння учнями інших груп

В класі біля стола кожної групи стоїть 6 стільців. Скільки існує способів розміщення за столом 6 учнів? Р6 =6! Р6 = 1•2•3 •4• 5• 6 = 720

II група Розміщення

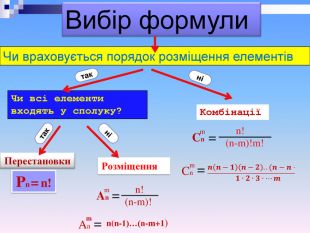
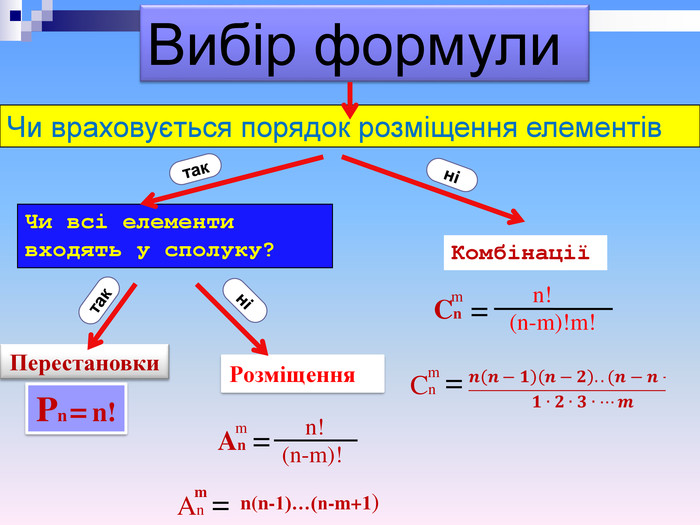
Розміщенням з m елементів по n називається будь-яка впорядкована підмножина з n елементів даної множини М, яка містить m елементів, де n  m. Характеристичні ознаки предмети і місця різні всі n місць треба зайняти порядок елементів важливий Число розміщень з m елементів по n позначається Am n n n

Скільки двоцифрових чисел можна утворити з цифр 1, 2, 3, 4, не повторюючи їх у запису числа? 2

Скільки двоцифрових чисел можна утворити з цифр 1, 2, 3, 4, не повторюючи їх у запису числа? 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3 12 13 14 21 23 24 31 32 34 41 42 43

У класі з 25 учнів, вибирають команду – 5 учнів: один – капітан команди, по одному учню – для участі в різних конкурсах. Скільки існує варіантів вибору? Розв’язання. В даній задачі важливий порядок розміщення елементів і не всі вони входять в сполуку,тому обираємо формулу розміщення : В даній задачі враховується порядок розміщення елементів і не всі елементи входять у сполуку, тому обираємо формулу розміщення.

Учню треба скласти 4 екзамени на протязі 8 днів. Скількома способами це можна зробити? 10 спортсменів розігрують одну золоту, одну срібну і одну бронзову медалі. Скількома способами ці медалі можуть бути розподілені між спортсменами? Із скількох різних предметів можна скласти 272 різних розміщень по два елементи в кожному? Задачі для перевірки розуміння учнями інших груп A8 4 A10 3

В 11 класі вивчається 14 предметів Скількома способами можна скласти розклад занять на понеділок, якщо в цей день повинно бути 6 різних уроків? A14 6 = 2 162 160 = 14• 13 • 12 • 11 • 10 • 9 Розклад

III група Комбінації

Комбінацією з m елементів по n називається будь-яка підмножина з n елементів даної множини М, яка містить m елементів Характеристичні ознаки предмети різні порядок елементів не має значення 0 ≤ n ≤ m Число розміщень з m елементів по n позначається n n Cm

У ящику лежить 12 білих і 8 чорних пронумерованих кульок. Скількома способами можна вибрати з ящика три кульки одного кольору? Розв’язання. Три кульки білого кольору можна вибрати способами, а три кульки чорного можна вибрати :спо спобами. За правилом суми 3 білих або три чорних можна вибрати 220+56=276 способами.

У шаховому гуртку 5 хлопців і 3 дівчини. Для зустрічі з гросмейстером прийшло 3 запрошення. Скількома способами можна розподілити запрошення так, щоб на зустріч попала хоча б одна дівчина. 3 3 В усіх інших виборах будуть приймати участь дівчата. Отже, таких виборів 56-10=46

Із 20учнів треба виділити 6 для чергування. Скількома способами це можна зробити? На полиці є 35 книжок. Скількома способами можна вибрати дві із них? У вазі 6 червоних і 4 білих троянди. Скількома способами з вази можна вибрати: 1) три троянди; 2) дві червоні і одну білу троянду? Задачі для перевірки розуміння учнями інших груп С20 6 С35 2

25 учнів потиснули один одному руки перед уроком. Скільки було зроблено рукостискань? С25 2 = 300

Яка Ваша думка щодо основної функції теорії комбінаторики? Охарактеризуйте свій емоційний стан протягом та в кінці уроку Які пізнавальні процеси були задіяні на уроці найбільше? Розвитку яких рис характеру сприяв урок? Який життєвий досвід ви отримали?