Englishdfsdfsdfsdfsdfsdfsdfsdfsdfsdf

Тема: Перетворення вираз Формули:

1.     (−1)^2𝑛 = 1

(−1)^2𝑛+1 = −1

2.     −(𝑎 + 𝑏) = −𝑎 − 𝑏;

−(𝑎 − 𝑏) = −𝑎 + 𝑏;

3.     𝑎² − 𝑏² = (𝑎 − 𝑏)(𝑎 + 𝑏)

4.     (𝑎 + 𝑏)² = 𝑎² + 2𝑎𝑏 + 𝑏²

(𝑎 − 𝑏)² = 𝑎² − 2𝑎𝑏 + 𝑏²

5.     𝑎³ + 𝑏³ = (𝑎 + 𝑏)(𝑎² − 𝑎𝑏 + 𝑏²)

𝑎³ − 𝑏³ = (𝑎 − 𝑏)(𝑎² + 𝑎𝑏 + 𝑏²)

6.     (𝑎 + 𝑏)³ = 𝑎³ + 3𝑎²𝑏 + 3𝑎𝑏² + 𝑏³

(𝑎 − 𝑏)³ = 𝑎³ − 3𝑎²𝑏 + 3𝑎𝑏² − 𝑏³

7.     (𝑎 + 𝑏 + 𝑐)² = 𝑎² + 𝑏² + 𝑐² + 2𝑎𝑏 + 2𝑏𝑐 + 2𝑎𝑐

Приклади:

1.     Розкладіть на множники: 𝑥² − 6𝑥 − 16

𝑥² − 6𝑥 − 16 = 𝑥² − 2 ∙ 3𝑥 + (3)² − (3)² − 16 = (𝑥 − 3)² − 9 − 16 =

= (𝑥 − 3)² − 25 = (𝑥 − 3)² − (5)² = (𝑥 − 3 − 5)(𝑥 − 3 + 5) = = (𝑥 − 8)(𝑥 + 2)

2.     Розкладіть на множники: 𝑥² − 5𝑥 + 4

𝑥² − 5𝑥 + 4 = 𝑥² − 5𝑥 + 4 + 1 − 1 = 𝑥² − 1 − 5𝑥 + 5 = (𝑥 − 1)(𝑥 + 1) −

−5(𝑥 − 1) = (𝑥 − 1)(𝑥 + 1 − 5) = (𝑥 − 1)(𝑥 − 4)

3.     Розкладіть на множники: 𝑎⁴ − 𝑏²(2𝑎 − 𝑏)²

𝑎⁴ − 𝑏²(2𝑎 − 𝑏)² = (𝑎² − 𝑏(2𝑎 − 𝑏))(𝑎² + 𝑏(2𝑎 − 𝑏)) =

= (𝑎² − 2𝑎𝑏 + 𝑏²)(𝑎² + 2𝑎𝑏 − 𝑏²) = (𝑎 − 𝑏)²(𝑎² + 2𝑎𝑏 − 𝑏²)

4.     Розкладіть на множники: 𝑎⁴ − 𝑏²(2𝑎 − 𝑏)²

𝑎⁴ − 𝑏²(2𝑎 − 𝑏)² = (𝑎² − 𝑏(2𝑎 − 𝑏))(𝑎² + 𝑏(2𝑎 − 𝑏)) = = (𝑎² − 2𝑎𝑏 + 𝑏²)(𝑎² + 2𝑎𝑏 − 𝑏²) = (𝑎 − 𝑏)²(𝑎² + 2𝑎𝑏 − 𝑏²)

5.     Спростіть вираз:

6.     Знайдіть значення виразу: 53 ∙ 39 + 47 ∙ 39 − 53 ∙ 21 − 47 ∙ 21

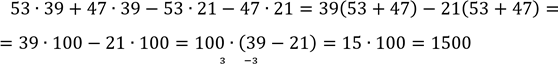
7.     Знайдіть значення виразу:

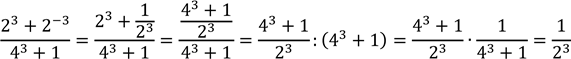
8.     Знайдіть значення виразу за певних умов: 

Знайдіть значення виразу 𝑎² + 𝑏².

 (𝑎 + 𝑏) = 𝑎 + 2𝑎𝑏 + 𝑏   ⟹ 𝑎 + 𝑏 = (𝑎 + 𝑏) − 2𝑎𝑏𝑎² + 𝑏² = (5)² − 2 ∙ 6 = 25 − 12 = 13.

9.     Доведіть, що при будь якому наступальному 𝑛, вираз

3^𝑛+2 −  2^𝑛+2 + 3^𝑛 −  2^𝑛 ділиться на 5

          3𝑛+2 −  2𝑛+2 + 3𝑛 −  2𝑛 = 3𝑛+2 + 3𝑛 −  2𝑛+2 −  2𝑛 = 3𝑛(32 + 1) −      −2^𝑛(2² + 1) = 10 ∙ 3^𝑛 − 2^𝑛 ∙ 5 = 5(2 ∙ 3^𝑛 − 2^𝑛) ⋮ 5       Доведено.

Завдання:

1.     Розкладіть на множники : 1) 𝑏² + 7𝑏 + 12

2)                𝑥⁴ + 4𝑥² + 4𝑥² − 9

3)                𝑦⁸ − 𝑦⁴ + 4𝑦² − 4

4)                𝑥³𝑦² + 𝑥²𝑦 − 2 + 𝑥²𝑦² + 𝑥𝑦 − 2𝑥

5)                𝑥³ − 2𝑥² − 5𝑥 + 6

6)                𝑥³ − 3𝑥² + 4𝑥 − 2

7)                (𝑎𝑦 + 𝑏𝑥)² + (𝑎𝑥 − 𝑏𝑦)² − 𝑐²(𝑥² + 𝑦²)

8)                𝑎²𝑐² + 𝑏²𝑑² − 𝑏²𝑐² − 𝑎²𝑑² − 4𝑎𝑏𝑐𝑑

9)                𝑚² + 𝑛² + 2𝑚𝑛 + 2𝑚 + 2𝑛 + 1

10)            𝑎𝑥² − 𝑏𝑥² − 𝑏𝑥 + 𝑎𝑥 + 𝑎 − 𝑏

11)            (𝑎 + 𝑏)² − 𝑐² + 𝑎 + 𝑏 + 𝑐

12)            8𝑥³ − 5𝑥² + 5𝑥 + 3

2. 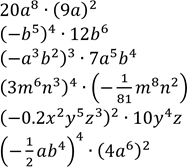    Спростіть вираз: 1)

2)

3)

4)

5)

6)

3.     Знайдіть значення виразу:

1)

2)

3)

4) 5) 6)

7)