Етапи формування навичок розв’язання нерівностей з двома змінними

 

ЕТАПИ ФОРМУВАННЯ НАВИЧОК РОЗВ'ЯЗАННЯ НЕРІВНОСТЕЙ І СИСТЕМ НЕРІВНОСТЕЙ З ДВОМА ЗМІННИМИ

1. Розвиток математичних компетентностей – важливе завдання шкільного курсу математики

 Для активізації пізнавальної діяльності учнів і логічного мислення перед вивченням теми необхідно  провести відповідну роботу з повторення знань та вмінь учнів щодо означення функції, властивостей основних елементарних функцій та деяких властивостей нерівностей. Методом поступового ускладнення завдань дійти до вивчення нового  матеріалу ( див. схему).

 

Підготовча тематика навчальної діяльності учнів при вивченні теми «Системи нерівностей з двома змінними»

 

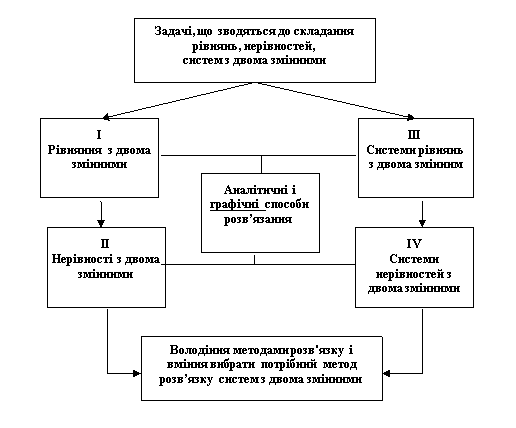
Основні етапи викладання теми « Розв’язування нерівностей і систем нерівностей з двома змінними»

1. Мотивація вивчення теми: вибір прикладних задач, які зводяться до складання нерівностей і систем нерівностей з двома змінними.
2. Складання математичної моделі задач.
3. Використання інноваційних методів проведення  даного уроку.
4. Розкриття графічних методів розв’язання .
5. Творча діяльність при виборі методів розв’язування систем нерівностей з двома змінними: порівняльний аналіз множини розв’язків нерівностей в системі ( використання палетки).
6. Узагальнення і систематизація знань учнів по даній темі.

В роботі з мотивації за даною темою я пропоную прикладні задачі, математичною моделлю розв’язування яких є нерівності. Основна мета цієї роботи – практична спрямованість уроків математики за рахунок правильного добору задач, які демонструють можливості застосування вивченого матеріалу та реалізацію ключових компетентностей учнів.

 Варто розпочати з найпростіших задач, у яких поняття нерівності закладено в умові, але для розв’язання задачі можна обійтися і рівнянням, або розв’язати задачу добором. Важливо переконати учнів в тому. що кожна абстрактна задача може бути математичною моделлю деякої прикладної задачі. Розкриття практичного і прикладного значення матеріалу, що вивчається, – один з ефективних прийомів прикладного спрямування шкільного курсу математики. Цьому сприяють задачі-запитання, розв'язування яких супроводять розглядом навколишніх об'єктів.

Умови таких задач наближують до практичних потреб, якими цікавляться учні. Працюючи над цією  проблемою, я застосовую у своїй роботі такі методи і прийоми: 1) розв'язування задач за готовими

 малюнками ; 2) роботу в групах; 3) прийом "Знайди помилку!"; 4) прийом "Заповни пусті місця!"; 5) вправу "Продовжити речення!; 6) дослідити математичний об’єкт і зробити висновки; 7) обзорові  графічні диктанти;

8) уроки презентації розв’язку задач з параметрами.

 

 

2. Методика розв’язування рівнянь з двома змінними графічним способом

Рівняння виду F (x; y) = 0,  де х і у – змінні, називається рівнянням з двома змінними.

Степінь цілого рівняння з двома змінними F (x; y) = 0 визначається як степінь многочлена F (x; y), якщо він зведений до стандартного вигляду.

а) Рівняння першого степеня: ах + bу + с = 0, ( а² + b² ≠ 0);

б) рівняння другого степеня: ах² + bу² + сху + dх + еу + f = 0,

 ( а² + b² + с² ≠ 0).

 Розв’язком рівняння з двома змінними х і у є впорядкована пара (x; y), яка перетворює рівняння на правильну рівність.

 Графіком рівняння з двома змінними х і у є множина точок координатної площини з координатами (x;y), де пара (x;y) є розв’язком даного рівняння.

Графіком рівняння першого степеня є пряма; графіком рівняння (х − a)² + (y − b)² = R², де R² ≠ 0 є коло з центром в точці  (а;b) і радіусом R; графіком рівняння у = ах² + bх + с, де а ≠ 0 є парабола.

Лінійні рівняння з двома змінними

Рівняння виду ах + bу = с, де а, b і с — деякі числа, називається лінійним рівнянням з двома змінними х і у. Якщо коефіцієнти при змінних х і у не дорівнюють нуль, то таке рівняння називають рівнянням першого степеня з двома змінними.

Розв’язком рівняння з двома змінними називається пара чисел х і у, при яких рівняння перетворюється на правильну рівність.

Задача 1. Складіть рівняння з двома змінними за умовою задачі: « На 22 грн. купили кілька книжок по 5 грн. і географічних карт по 3 грн. Скільки купили книжок і карт?

Нехай купили книжок по 5 грн. - х, а географічних карт по 3 грн. - у. Тому книжок і карт купили 5х+3у = 22

Як розв’язати таке рівняння?

1.  Знайти розв'язки рівняння 5х + 3у = 22 можна так: підставити в нього замість х довільне число, наприклад 2. Дістанемо рівняння з однією змінною: 5·2+3 у = 22. Розв'язавши його, знайдемо, що у=4. Пара чисел (2;4) — розв'язок рівняння  5х+3у = 22.
2.  Виразити одну змінну через другу.

Для знаходження розв'язків рівняння 5х+3у = 22 зручно виразити одну змінну через другу. Виразимо, наприклад, змінну х через у. Для цього перенесемо доданок 3у до правої частини, змінивши його знак: 5х = 22-3у. Поділимо обидві частини цього рівняння на 5, дістанемо: х = 4,4-0,6у. Враховуючи вище зазначене, можна зробити висновок, що рівняння  х = 4,4-0,6у рівносильне рівнянню 5х + 3у = 22. Із формули х = 4,4-0,6у можна знайти скільки завгодно розв’язків рівняння 5х + 3у = 22. Наприклад, якщо у=1, то х =4,4 - 0,6 = 3,8; якщо у = 2, то х = 4,4·0,6-2 = 3,2 і т. д. Отже, рівняння 5х + 3у = 22 має безліч розв'язків.

Розв’яжемо дане рівняння графічним методом.

Виразимо у через х: у = , графіком цієї функції є пряма, яку ми будуємо в координатній площині (див. рис.)

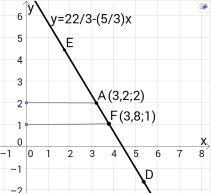Наприклад, точки А(3,2;2),F(3,8;1),D,E належать прямій у =, тому координати цих точок є розв’язками даного рівняння. Графік рівняння підтверджує нескінченну множину його розв’язків.

 

Як побудувати графік рівняння з двома змінними?

1. Якщо рівняння можна звести до вигляду (х − а)² + (у − b)² = R² де а і b ─ довільні числа, а R > 0, то графіком цього рівняння буде коло з центром (а; b) і радіусом R.
2. Якщо рівняння можна звести до вигляду у = ах² + bх + с, де а ≠ 0, то графіком буде парабола.
3. В інших випадках (якщо немає модуля) виражаємо у через х і будуємо графік утвореної функції у = f (х).

Рівняння другого степеня

Задача 2. Знайти точку, яка рівновіддалена від точок В(2,3), С(6,-1) та лежить на осі абсцис.

Нехай шукана точка має координати (х, у).Тоді за умовою задачі складаємо рівняння  (х-2)² +(у-3)² = (х-6)² + (у+1)² (*) . Оскільки за умовою задачі шукана точка має координати (х,0), то рівняння перетворюється на рівняння виду

(х-2)² +(-3)² = (х-6)² + (0+1)² , звідси х = 3. Шукана точка А(3,0).

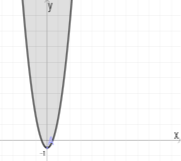
 Розв’яжемо рівняння (*) графічним методом.

Побудуємо графіки функцій лівої і правої частин рівності в координатній площині.

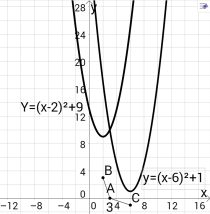
f(x)= (х-2)² +9, g(x)= (х-6)² +1(див. рис.). Параболи перетинаються в точці, координата х якої дорівнює 3.

Задача 3. Знайти декілька розв’язків рівняння

 х² + у² = 4(**).

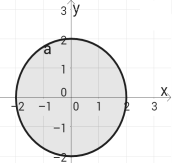
Графіком рівняння є коло з центром (0,0) і R=2.

 Підставляємо в рівняння замість х довільне число, наприклад 4. Дістанемо рівняння з однією змінною: 16+ у² = 4. Розв'язуючи його, отримуємо

 у² = -12, що неможливо і робимо висновок, що х=4 не може бути розв’язком рівняння. Спробуємо інший метод. Виразимо у² через х, у² = 4 - х² . Нехай х =, тоді у²  = 1, у = -1 або у = 1. Пара чисел

 (;-1), (;1) — розв'язки рівняння.

Розв’яжемо рівняння (**) графічним методом (див. рис.).

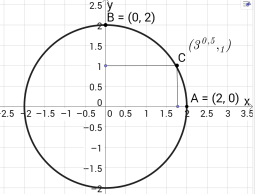Точки С(;1), A(2,0), B(0,2)  належать колу, тому їх координати (х, у) є розв’язками рівняння(**).

Кожне рівняння першого степеня з двома змінними має безліч розв’язків.

На даному етапі доцільне виконання усних вправ.

Усні вправи:

•                    а) чи є розв’язком рівняння х² + у = 10 пара чисел ?

(3; 1); 2) (−2; 6); 3) (1;−3)

•                    б) виразіть одну змінну через іншу і знайдіть два будь-які розв’язки

рівняння:1) х² − у + 15 = 0; 2) 2х + 3у + ху = 2;

•                    в) чому пара чисел х = -1; у = 5 не є розв’язком цього рівняння

 х + у² = 30?

•                    г) наведіть приклади рівнянь з двома змінними, графіками яких є:

1) коло;2) пряма;3) гіпербола;4) парабола;

•                    д) підберіть декілька розв'язків рівняння:1) х - у = 10; 2) х у = 10;

3) х /у = 10;

•                    е) яку загальну властивість має будь-яка точка графіка даного рівняння з двома змінними?

.3 Нерівності з двома змінними та їх геометричний зміст

Розв’язування алгебраїчних та геометричних задач часто призводить до необхідності розв’язувати системи рівнянь з двома змінними. Одним із ефективних методів їх розв’язання є графічний метод. Метод координат дозволяє геометрично тлумачити не тільки рівняння, а також і нерівності.   Подібно тому, як ми говоримо, що рівняння з двома змінними х та у

F(х, у) = 0 визначає на площині деяку лінію, можна сказати, що нерівність з двома змінними х та у F(х, у) < 0 визначає множину точок площини, координати яких задовольняють цій нерівності. Таким чином геометрично тлумачать і нерівність F (х, у) > 0.

Якщо вираз F (х, у) є лінійним, тобто F (х, у) = Ах + Ву + С, де А, В, С сталі, то ми маємо лінійне рівняння Ах + Ву + С = 0 (*)

та дві лінійні нерівності Ах + Ву + С < 0 (**), Ах + Ву + С > 0 (***).

Якщо коефіцієнти А і В не дорівнюють одночасно нулю, то рівняння (*) визначає на площині пряму, а нерівності (**) і (***) — відповідно дві півплощини, на які пряма (*) розбиває всю координатну площину. Для того щоб з'ясувати, яка із цих двох півплощин визначається заданою лінійною нерівністю, можна застосувати, наприклад, такий спосіб.

Виберемо яку-небудь точку, підставляємо її координати в нерівність, що перевіряється.

Якщо координати точки задовольняють нерівність, то нерівність визначає ту площину, в якій знаходиться вибрана точка; якщо ж координати точки не задовольняють нерівність, то нерівність визначає площину, яка не містить вибраної точки.

Рішенням нерівності F(x;y)>0 називають всяку пару чисел (x;y), яка задовольняє цій нерівності, тобто обертає її в правильну числову нерівність.

Задача1. Записати з допомогою нерівності ту півплощину, в якій лежить точка А(4;5) та границею якої є пряма 3х+2у+5 = 0. Перевірити, лежить в цій же півплощині початок координат.

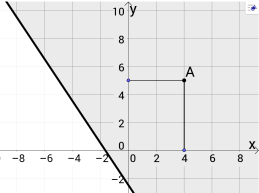Розв'язок. Підставимо координати точки А в ліву частину рівняння заданої прямої: 12+10+5 = 27. Одержана величина додатна. Отже, точка А не лежить на заданій прямій, а шукана площина визначається нерівністю 3х+2у+5 > 0.

Геометричний розв’язок( див. рис.)

Виражаємо змінну у через змінну х:

у = -2,5-1,5х (графік-пряма). Будуємо графік в координатній площині і показуємо область розв’язків нерівності 3х+2у+5 > 0 (див. рис.). Точка А належить півплощині, множина точок якої є розв’язком нерівності. За малюнком можна привести немало прикладів точок, координати яких задовольняють нерівність.

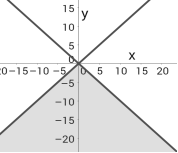
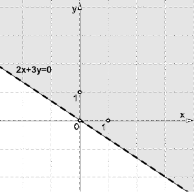
Приклад. Розв'язати нерівність 2x+3y > 0.

Побудуємо графік рівняння 2x+3y = 0 - пряму.

Рішенням нерівності є точки напівплощини вище або нижче побудованої прямої.
Для правильного визначення потрібної напівплощини виберемо будь-яку точку з неї, координати якої підставимо в таку нерівність.

Якщо нерівність буде вірною, то напівплощина вибрана вірно(див. рис.).

Вибравши контрольну точку (1;1) з верхньої напівплощини, отримаємо правильну числову нерівність: 2⋅1+3⋅1 > 0.

Значить, рішенням даної нерівності є верхня напівплощина.

Задача 2. Мишко, Віталік та Олег вирішили купити одну книжку. Мишкові не  вистачило на покупку книжки 15 грн., Віталікові - 37 грн., а Олегові - 25 грн. Склавши гроші, хлопці виявили, що отриманої суми знов не вистачає на покупку. Скільки коштує книжка, якщо її вартість виражається цілим числом гривень?

Нехай книжка коштує х грн., тоді в Мишка було (х-15) грн., у Віталіка – (х-37) грн., а в Олега – (х-26) грн.. Складаємо та розв’язуємо нерівність

(х-15)+(х-37)+(х-26) < х; 3х-78 < х, х < 39. З другого боку, х > 37, оскільки у Віталіка була деяка сума грошей. Отже, 37 <х< 39, тобто х = 38 (грн.) ( див. рис.).

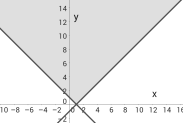
Приклад. Розв'язати нерівність х²- 4х+у²+6у-12 > 0.

Виділяємо повний квадрат: (х-2)²+(у+3)² > 25.

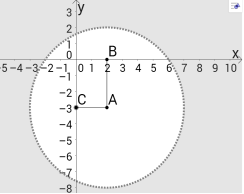Графіком рівняння (х-2)²+(у+3)² = 25 є коло з центром (2,-3) і R=5. Вибираємо пробну точку з внутрішньої області (2,-3) і підставляємо її координати в нерівність: (2-2)²+(-3+3)² >25, 0 > 25- невірно. Робимо висновок, що дана нерівність не виконується у  внутрішній області. Вибираємо пробну точку ззовні (8,-3): (8-2)²+(-3+3)² = 36 > 25, тому нерівність виконується у зовнішній області, границя області - коло ( зображено пунктирною лінією, оскільки нерівність строга, див. рис.)

На даному етапі доцільне виконання усних вправ.

Усні вправи:

№ з/ п	Вправи	Схематичний розв'язок
1.	Сьогодні у Києві 0ºС, а в Харкові температура не вища за київську.	Температура в Харкові (х): х ≤ 0
2.	Вода піднялася на висоту не менше 5м	Висота(у): у ≥ 5
3.	Температура води в стані рідини при нормальному тиску не менше 0ºС і не більше 100ºС	Температура води (х): 0ºС≤х≤100ºС
4.	Якщо сторони прямокутника зменшити, одну на 2м, а іншу на 3м, то отримаємо квадрат, площа якого буде відрізнятися від площі прямокутника менше, ніж на 16 м2 Знайти сторони квадрата та прямокутника, знаючі, що міри довжини вимірюється цілими числами.	х - сторона квадрата, тоді (х+3)-довжина, (х+2) –ширина прямокутника. Площа квадрата - х2, площа  прямокутника (х+2)(х+3).-х2< 16, 5 х < 10; х < 2, але х належить N. Сторона квадрата 1м, сторони прямокутника 3м і 4м.
5.	Довжина розбігу літака під час зльоту не менше 80 м	z- довжина розбігу, тому z ≥ 80
6.	Яка ймовірність того, що навмання взяте число, що менше 100 ділиться на 5 або на 7?	31/99
7.	Що є графіком нерівності х > a, x < a?	х > a – усі точки координатної площини, які розташовані праворуч від цієї прямої; x < a – розташовані ліворуч.
8.	Що є графіком нерівності х2+ у2 < R2, х2+ у2 > R2?	Усі точки координатної площини, які розташовані всередині кола (поза колом).
9.	Графік якої нерівності зображено на рисунку?       а)                                                          б)	а) х2+ у24; б)у х2-1.
10.	На якому рисунку зображено графік нерівності: у     а)     б)	а)