Факультативне заняття "Методи розв'язування рівнянь вищих степенів"

Міністерство освіти і науки України

 Хорошівська гімназія

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розробка факультативних занять з математики по темі:

 

 

• «Рівняння вищих степенів та методи їх розв’язування»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

               З досвіду роботи

        вчительки математики

        Хорошівської гімназії

        Микитенко Анни Пилипівни

 

Рівняння вищих степенів та методи їх розв’язування

 Під раціональними рівняннями розуміють рівняння, що можна записати у вигляді:

  a_nxⁿ+ a_n-1x^n-1+… a_ixⁿ+ a₀=0, де

  a_n, a_n-1,... a₀ – задані числа, а х – невідоме.

 

Методи розв’язування рівнянь

І. Групування: шляхом групування доданків доданків, примінення формул скороченого множення звести (якщо це вдається) рівняння до вигляду, де зліва записано добуток декількох множників, а справа – нуль. Потім прирівнюємо до нуля кожний множник.

Приклади.

1). х³-(а+в+с)х²+(ав+ас+вс)х-авс=0,

 х³-ах²-вх²-сх²+авх+асх+всх-авс=0,

 групуємо: х²(х-а)-вх(х-а)-сх(х-а)+вс(х-а)=

 =(х-а)(х²-вх-сх+вс)=0

 х-а=0    або  х²-вх-сх+вс=0,

 х₁=а    х(х-в)-(х-в)с=0,

 (х-в)(х-с)=0,

 х-в=0 або  х-с=0

 х₂=в         х₃=с

   Відповідь: х₁=а, х₂=в, х₃=с

 

 2). х³-3х+2=0. Перепишемо рівняння, записавши -3х=-х-2х

  х³-х-2х+2=0

  х(х²-1)-2(х-1)=0,

  (х-1)(х(х=1)-2)=0.

  х-1=0,  х²+х-2=0

  х₁=1  х₂=-2, х₃=1

       Відповідь: х₁=х₃=1; х₂=2

 

 ІІ. Підстановки: шукаємо в рівнянні деякі вирази, що повторюються, які позначаємо новою змінною, тим самим спрощуємо вигляд рівняння. В деяких випадках видно, що позначити новою змінною, а в деяких треба виконати спочатку тотожні перетворення. В інших випадках зручно підстановку робити знаючи „наперед”.

Приклади.

1). (х-4)(х-5)(х-6)(х-7)=1680,

 (х²-11х+28)(х²-11х+30)=1680.

Постачимо х²-11х+28=t, тоді:

 t(t+2)=1680.  t₁=-42, t₂=40. Звідси

 х²-11х+28=-42  або   х²-11х+28=40

 х²-11х+70=0        х²-11х-12=0

 х є Ø      х₁=12, х₂=-1

       Відповідь: х₁=-1; х₂=12

 2). Симетричні рівняння (коефіцієнти членів, які знаходяться на однаковій відстані, рівні)

  2х⁴+3х³-16х²+3х+2=0

 Розділимо дві частини рівняння на х²≠0,

одержимо ,

 

,

позначимо , тоді , звідси

                        .

Одержимо:

2(t²-2)+3t+(-16)=0,

2t²+3t-20=0,

t₁=-4, .  ,  

       x₃=2,

       Відповідь: , x₃=2, .

 

 3). (х²+х+1)(х²+х+2)=12. Позначимо:

  х²+х=а, тоді маємо:

  (а+1)(а+2)=12

  (а²+3а-10=0

  а₁=2,  а₂=-5

  х²+х=2, або х²+х=-5,

  х²+х-2=0,  х²+х+5=0

  х₁=1, х₂=-2  х є Ø

Відповідь: -2, 1

 

 4). (2х²-3х+1)(2х²+5х+1)=9х²

 

  Поділимо на .

  

   Замінимо

  (t-3)(t+5)=9,

  t²+2t-24=0

  t₁=4, t₂=-6 Тоді   або 

       

       Відповідь: ;

 

ІІІ. Підбір: при розв’язуванні рівнянь вищих степенів раціональні корені рівняння

a_nxⁿ+ a_n-1x^n-1+… a_ixⁿ+ a₀=0 шукаємо серед чисел виду , де Р – дільник вільного члену, Q – дільник ст. коефіцієнта (а_n) Р і Q взаємно прості, Р є Z, Q є N.

 

 

Приклади.

1). х³-х²-8х+6=0.

а_n=1, а₀=6. Тому, якщо дане рівняння має корені, то їх слід шукати серед дільників числа 6: ±1; ±2; ±3; ±6. перевіркою переконуємося, що х=3. Ділимо ліву і праву частину рівняння на х-3.

_х³-х²-8х+6     |x-3

 x³-3x²              |x²+2x-2

  _2x²-8x

    2x²-6x

      _-2x+6

        -2x+6

     0

Тоді   х³-х²-8х+6=(х-3)(х²+2х-2)=0

Звідси  х₁=3,  

 

      Відповідь: х₁=3, 

 

2). 2х⁴-3х³-7х³+6х+8=0

 а_n=2, a₀=8 Раціональні корені слід шукати серед чисел ±1; ; ±2; ±4; ±8.

Перевіркою переконуємося, що х=-1 – корінь рівняння, тому

_2х⁴-3х³-7х²+6х+8          |x-3

 2x⁴-2x³                            |2x³+5x²-2х+8

  _-5x³-7x²

    -5x³-5x²

      _-2x²+6х

        -2x²-2х

             _8х+8

               8х+8

                      0

Дане рівняння можна записати: 2х⁴-3х³-7х²-6х+8=(х+1)( 2х³-5х²-2х+8)=0.

Аналогічно знаходимо корінь рівняння 2х³-5х²-2х+8=0, х=2. Знову ділимо на х-2.

_2х³-5х²-2х+8       |x-2

  2х³-4х²

       _-x²-2x

         -x²+2x

 _-4x+8

   -4x+8

          0

Тоді маємо: 2х⁴-3х³-7х²-6х+8=(х+1)(х-2)( 2х²-х-4)=0

Звідси х₁=-1, х₂=2, .  

Відповідь: х₁=-1, х₂=2, .

IV. Нестандартний.

Приклади.

1).  

Поділимо чисельник і знаменник дробу на х ≠ 0

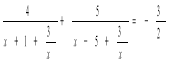 Позначимо , одержимо:

, t ≠ -1, t ≠ 5.

8t-40+10t+10+(3t+3)(t-5)=0,

3t²+6t-45=0,

t²+2t-15=0

t₁=3, t₂=-5, звідси:  ,  

    х ≠ 0.   х ≠ 0.

    х²-3х+3=0  х²-5х+3=0

    х є 0   .

 

     Відповідь: .

 

 2).  . Виділимо повний квадрат, додавши і віднявши в лівій частині рівняння х².

 , . Нехай х²-х=t, тоді:

, . Вернемося до змінної х.

Маємо:  або

  

х ≠ 0.    

    Відповідь:

 3). (3х²+7х-2)²+5х²(3х²+7х-2)-24х⁴=0

 Це „однорідне” рівняння, тобто рівняння виду ay^2λ+by ^λz ^λ+cz^{2 λ}=0, де а,в,с, λ – задані числа відмінні від нуля; y=y(x), z=z(x) – деякі функції від х. Ділимо обидві частини рівняння на z^{2 λ} ≠ 0 (на функцію у вищому степені). Одержимо:

. Позначимо , одержимо квадратне рівняння відносно t.

Поділимо на х⁴ ≠ 0, одержимо:

.

Нехай , маємо:

t²+5t-24=0

t₁=3, t₂=-8 Тоді: а)  або б)

а)  3х²-3х²+7х-2=0    б) 3х²+8х²+7х-2=0

        11х²+7х-2=0

        Д=49+88=137

        

      Відповідь: ; .

 

4).  

Користуючись формулою а²+в²=(а-в)²+2ав, одержимо:

,

,

,

.

Нехай , тоді маємо: а²+6а-7=0.

     а₁=1, а₂=-7

 або 

 х ≠ -3 х²-х-3=0, х ≠ -3

х є Ø   

      Відповідь: 

 

5). 

 Д(f): х≠-1, х≠-2, х≠1.

В прикладах, де ліва частина являє собою суму дробів, в кожному дробі виділяють цілу частину (ділять чисельник на знаменник).

_2х-1 |x+1 ,  _3х-1 |x+2 ,  _х-7  |x-1

 2x+2 |2 3x+6  |3 x-1   |1  , тоді маємо

      -3                    -7                -6

 

4х²-15х-25=0

Д=625

; .

      Відповідь: ; .

 

V. Різні методи розв’язування.

Приклади.

1). (х-1)х(х+1)(х+2)=24,

 (х-1)(х+2)х(х+1)=24,

 (х²+х-2)(х²+х)=24.

Нехай х²+x=t, тоді

t(t-2)=24

t²-2t-24=0

t₁=-4, t₂=6. Перевіримо для змінної х

х²+х=6 або х²+х=-4

х²+х-6=0  х²+х+4=0

х₁=-3, х₂=2  х є Ø

      Відповідь: х₁=-3, х₂=2

 

2). (х+2)(х+3)(х+8)(х+12)=4х²,

 (х²+14х+24)(х²+11х+24)=4х² поділимо на х² ≠ 0.

 

 Нехай

(t+14)(t+11)=4,

t²+25t+150=0,

t₁=-15, t₂=-10. Тоді:  або 

    х²+10+24=0   х²+15х+24=0

    х₁=-6, х₂=-4   

     Відповідь: х₁=-6; х₂=-4; .

 

4). 

Поділимо чисельник і знаменник дробу на х ≠ 0

 

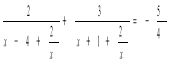
Нехай , тоді ; y ≠ -1; y ≠ 4

4(2y+2)+4(3y-12)+5(y-4)(y+1)=0

5y²+5y-60=0,

y²+y-12=0

y₁=-4, y₂=3   або 

   х²+4х+2=0  х²-3х+2=0

     x₁=1, x₂=2

      

      Відповідь: , 1, 2.

 

5). 

 

 

  х ≠ 2

Нехай

y²-8y-20=0

Д=144

у₁=10, у₂=-2  Перейдемо до змінної х

 

,     ,

2х²-10х+20=0    2х²=-2х+4=0 ,

Д<0, х є Ø     2х²+2х-4=0

      

      х₁=-2, х₂=1

     Відповідь: х₁=-2, х₂=1

 

Опрацюй самостійно:

1). х⁴-2х³-13х²+14х+24=0  В.: -1; 2; -3; 4.

2). (х²+5х)²-2(х²+5х)-24=0  В.: ±1; -6; -4.

3). (х-4)(х-5)(х-6)(х-7)=1680  В.: -1; 12.

4).    В.: .

5).  В.: х₁=2; х₂=0,75.