Урок "Перетворення графіків функцій"

Тема уроку: Побудова графіків функцій і рівнянь за допомогою геометричних перетворень

Предметна компетентність:

• удосконалювати навички перетворення графіків функцій та побудови графіків функцій з використанням перетворень графіків;

• вчитися розпізнавати функцію за її графіком;

Інформаційно-комунікаційна компетентність

• впровадження інформаційно - комп’ютерних технологій навчання;
• залучення учнів до роботи з різними джерелами інформації;
• удосконалення вмінь використовувати додаткову літературу, складати схеми, таблиці;

Соціальна компетентність

• використання групових, парних, колективних форм організації навчальної діяльності;
• упровадження технологій і методів навчання, що сприяють формуванню правильної оцінки і самооцінки, умінь застосовувати власний досвід, адаптуватися до змін.

Громадянська компетентність

• вчити учнів аргументовано доводити власну точку зору.

Наскрізна лінія «Громадянська відповідальність»:

• виховувати увагу, активність, естетичний смак, почуття єдності та відповідальності за спільну справу.

Тип уроку: Урок повторення знань, умінь та навичок.

Обладнання: мультимедійний проектор; презентація; картки самоконтролю, опорний конспект.

Хід уроку

І. Організаційний момент.

II. Повідомлення теми. Постановка мети (слайд 1)

III.Мотивація навчальної діяльності (слайд 2)

Розглянемо зображення мосту. В конструкції цієї інженерної споруди використані елементи у вигляді графіків відомих елементарних функцій: прямі лінії, параболи, гіперболи. Саме такі форми, за інженерними розрахунками, забезпечують міцність і надійність цієї споруди. В сучасній математиці вивченню функцій приділяється особлива увага, адже за їх допомогою можна змоделювати явища, які відбуваються в природі, на виробництві та в суспільстві. Побудова графіків значно полегшує процес вивчення функцій. Спробуємо навчитись будувати графіки деяких функцій швидко і легко.

IV.Актуалізація опорних знань.

1. Бліц опитування (слайд 3)
2. Вправа “Мікрофон”(слайд 4)
3. Оголошення мети  уроку(слайд 5)

V. Повторення  знань даної теми за 9 клас

1. Симетрія відносно осі Ох. (слайд 7)
2. Паралельне перенесення вздовж осі ординат(слайд 8)
3. Паралельне перенесення вздовж осі абсцис(слайд 9)
4. Модуль в квадратичній функції. (слайд 10)

Вправа «Визнач положення параболи» (слайд 11-20)

VI.Відпрацювання вмінь і навичок

Математичне лото(слайд 21)

 Вправа: «Встанови відповідність»: поставити у відповідність до кожного графіка аналітичний запис відповідної функції

Практичне завдання (слайд 23)

Робота в групах з завданнями ЗНО (додаток А) на 10 хв (Скористайтеся опорними конспектами (додаток Б))

VIІ.Підсумок роботи

1. Оцінювання роботи: перевірка відповідей на екрані(слайд 24-25)
2. Рефлексія: (слайд 26)

Чи була досягнута зазначена мета уроку?

Чи сподобався вам урок? Чому?

Ваші пропозиції щодо подальшої співпраці.

3. «Нехай ця парабола - парасолька захищає вас від всяких негараздів» (слайд 27)

VIІІ. Домашнє завдання §2 підручник 9 класу(слайд 28)

https://uk.wikipedia.org/wiki/ перетворення графіків функцій

Додаток А

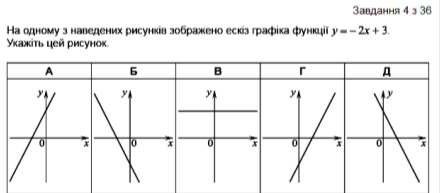
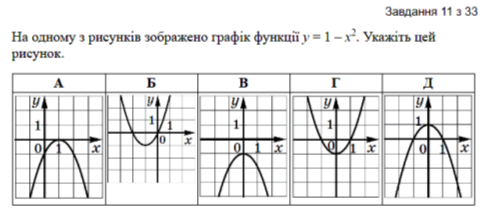
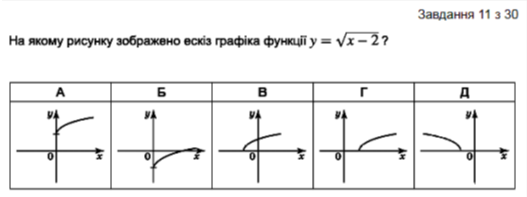
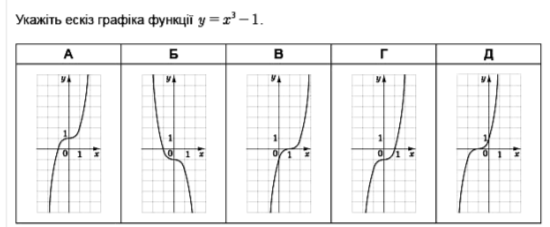
                                     С. 64 №24

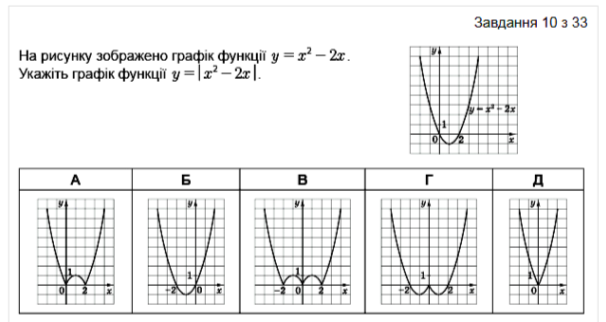
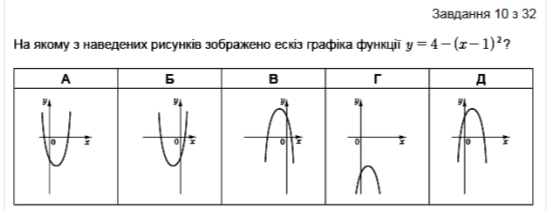
                           С.8 №26

Додаток Б

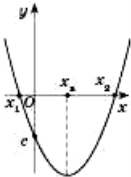
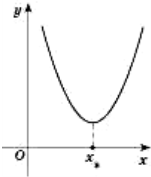
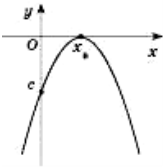
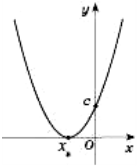
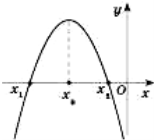
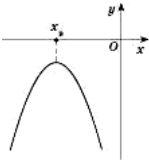
На рисунках, поданих нижче, наведені ескізи розміщення параболи на

 координатній площині в деяких випадках.

 Коефіцієнт а -  вітки вгору чи вниз,

                   в – визначається з знаку вершини параболи по Ох,

                  с – знак перетину вісі Оу