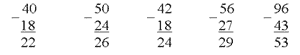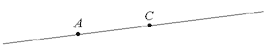Формування життєвих та ключових компетентностей учнів початкових класів при вивченні геометричного матеріалу
Харківський ліцей №149
Харківської міської ради Харківської області

В.Корбюзьє
Формування життєвих та ключових компетентностей
учнів початкових класів при вивченні
геометричного матеріалу
Підготувала
учитель початкових класів
Михайленко Інна Володимирівна
Харків
2018
ВСТУПЛЕНИЕ
Геометрия в 21-ом веке...
- Что нового может дать геометрия, как предмет устаревший, почти не изменившийся за последние несколько тысячелетий? – может подумать какой-нибудь невежда, не понимающий, что вся мировая наука начиналась именно с геометрии.
Еще в начале прошлого столетия великий французский архитектор Корбюзье изумленно воскликнул: «Все вокруг геометрия!». Сегодня, в начале 21 столетия, с не меньшим изумлением мы можем повторить это восклицание. В самом деле, посмотрите вокруг – всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики. Воистину, современная цивилизация – это Цивилизация Геометрии. Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых.
Задумайтесь сами.
Геометрия является феноменом общечеловеческой культуры. Некоторые теоремы геометрии являются одними из древнейших памятников мировой культуры. (Человек не может по-настоящему развиться культурно и духовно, если он не приобщился к эти памятникам, ведь геометрия возникла не только из практических, но и из духовных потребностей человека).
Геометрия отражает историю развития человеческой мысли, издавна являясь одним из самых мощных моторов, двигающих эту мысль. (Например, возникшая несколько тысячелетий тому назад теория конических сечений, пополненная законами, открытыми Кеплером, вымостила дорогу человечества в Космос).
Геометрия представляет собой очень действенное средство для нравственного воспитания человека. (В романе «Война и мир», характеризуя князя Николая Болконского, Л.Н.Толстой пишет: «Он говорил, что есть ... только две добродетели: деятельность и ум. Он сам занимался воспитанием своей дочери и, чтобы развить в ней обе главные добродетели, давал ей уроки алгебры и геометрии и распределил всю ее жизнь в беспрерывных занятиях).
Поэтому учитель начальных классов должен поставить перед собой задачу, показать младшим школьникам, что геометрия действительно находится вокруг нас, и, будучи феноменом общечеловеческой культуры, отражая историю развития человеческой мысли и являясь средством нравственного воспитания, заслуживает нашего пристального внимания и изучения.
Задача учителя вполне решаемая, если изначально рассматривать ученика как своего рода «чистый лист» (с точки зрения геометрических знаний), который следует заполнить ученику в определенной последовательности.
Поэтому учитель должен не только открыть дверь в науку Геометрию, но и достаточно долго держать ее открытой, чтобы заманить туда ученика. Учитель должен постараться развить в ученике в некотором смысле зависимость от геометрии, интеллектуальную, психологическую и, может быть, и физиологическую. (В начальной школе геометрия, по сути, является разновидностью физкультуры. Интеллектуальной физкультуры, включиться в занятия которой можно в любой момент). И тогда задача «заинтересовать» ученика геометрией будет учителем решена.
1. Формирование жизненных и ключевых компетентностей учащихся начальных классов
Как известно, человек не рождается с развитой, совершенной жизненной компетентностью. Развитие компетентности происходит в процессе познания, общения, деятельности, в отношениях с другими людьми, миром.
И чем выше уровень жизненной компетентности, тем успешнее человек построит свою жизнь.
От школы во многом зависит, какого уровня компетентности достигнет человек. Ведь ребенок проводит в школе более 10 лет. И несмотря на то, что школа не может выкроить и сшить жизнь ребенка такой, какой она должна быть, она все-таки может помочь ребенку развить жизненную компетентность.
Развить жизненную компетентность помогут хорошо сформированные ключевые компетентности, представляющие собой основной набор общих понятий, которые детализированы в комплекс знаний, умений, навыков, ценностей и отношений.
Существует много подходов к формированию ключевых компетентностей. Среди них:
- Интегрированное обучение как способ формирования ключевых компетентностей. При таком обучении ставка делается на достижение результата, который связан с умением учащихся использовать знания и собственный опыт в конкретных жизненных ситуациях. Достичь этого можно, если учащийся умеет оперировать научными знаниями, фактическим материалом, знания его связаны с окружающей дествительностью, жизнью общества, социальной деятельностью, если у ученика присутствует внутренняя мотивация, интерес, заинтересованность.
- Интерактивное обучение как способ формирования ключевых компетентностей. Мы живем в постоянно изменяющемся обществе, поэтому объект учения всегда будет меняющимся, а вот способ овладения этими объектами следует заложить в школьные годы – это умение работать с текстом, владение разными способами обработки информации, умение искать информацию, грамотно работать с ней, обобщать изученный материал.
- Метод проектов, в основе которого лежит развитие познавательных интересов и творческих навыков учащихся, при котором дети учатся самостоятельно добывать знания, проводить исследования, искать информацию, анализировать ее, делать выводы, обобщать итоги наблюдений и исследований.
- Технология развития критического мышления как способ формирования ключевых компетентностей представляет собой систему методических приемов, которые направлены на формирование у детей умения высказывать собственные мысли, формулировать собственную точку зрения, умение развязывать проблемы, работать в группе, способность строить конструктивные отношения с другими детьми.
Эти и многие другие педагогические технологии продуктивного обучения формируют и развивают группы ключевых компетентностей.
Являясь одной из древнейших отраслей математики, геометрия обладает
значительными возможностями в формировании жизненных и ключевых
компетентностей человека.
Она может и должна стать предметом, с помощью которого ученик овладеет жизненными и ключевыми компетентностями.
Геометрия, выражаясь образным языком, - это витамин для мозга. Только включив в работу мозг, можно добиться успеха в постоянно изменяющемся мире. Только овладев жизненными и ключевыми компетентностями, можно занять достойное место в этом мире.
Поэтому если основывать изучение геометрии на имеющемся у детей опыте взаимодействия с твёрдыми телами и их движением, связывать обучение с ощущениями учащихся, опираясь на естественное геометрическое развитие, то можно сделать геометрическое знание для ребёнка «живым», человеческим, имеющим самое непосредственное отношение к его повседневной жизни. А это, в свою очередь, поможет при формировании жизненных и ключевых компетентностей учащихся.
2. Содержание работы с геометрическими фигурами
Разделом программы «Геометрические фигуры и их свойства. Геометрические тела» предусмотрено ознакомление учащихся с многоугольником, четырехугольником, в том числе прямоугольником (квадратом) и его элементами: сторонами, углами, вершинами; учащиеся учатся находить периметр и площадь прямоугольника (в том числе квадрата).
Работа с этими геометрическими фигурами носит поступательный характер.
В первом классе учащиеся знакомятся с многоугольниками, (в том числе с четырёхугольниками). Дети должны:
– усвоить правильное название многоугольников;
– уметь их распознавать;
– определять знакомые геометрические фигуры в фигурах сложной конфигурации, на предметах окружающего мира, на рисунках;
– изображать схематично геометрические фигуры на бумаге в клеточку.
В процессе изучения нумерации чисел первого десятка практикуется составление многогранников из палочек, вырезание из бумаги, а также распознавание многоугольников на предметах окружающего мира и рисунках.
Во втором классе продолжается работа по формированию представлений
учащихся про многоугольники (в том числе прямоугольник и квадрат).
Учащиеся:
– различают геометрические фигуры;
– определяют элементы многоугольников: вершины, стороны, углы;
– обозначают геометрические фигуры буквами латинского алфавита;
– знают, что прямоугольник – это четырёхугольник, у которого все углы прямые;
– знают, что в прямоугольнике противоположные стороны равны;
– понимают, что квадрат – это прямоугольник с одинаковыми (равными) сторонами;
– строят прямоугольник и квадрат на бумаге в клеточку;
– знают, что периметр многоугольника – это сумма длин его сторон;
– находят периметр четырёхугольника.
Под конец обучения во 2-м классе вводятся упражнения и задания на распознавание многоугольников в конфигурациях фигур.
В третьем классе продолжается работа по формированию представлений
учащихся про периметр прямоугольника, (в том числе квадрата).
Учащиеся:
– находят периметр прямоугольника (квадрата);
– решают задачи, которые связаны с периметром прямоугольника.
При этом учащимся показываются разные способы вычисления периметра (а+в+а+в; а+а+в+в; а 2 + в 2; (а+в) 2).
В четвёртом классе учащиеся продолжают выполнять задания на распознавание плоских и объёмных геометрических фигур и построение плоских. Знакомятся с развёрткой куба и нахождением площади поверхности куба. Решают задачи с геометрическим содержанием. Геометрические задачи, связанные с периметром, несколько усложняются, большая часть из них связана с понятием площади фигуры.
Учащиеся:
– различают плоские и объёмные геометрические фигуры;
– строят развёртку куба по образцу;
– находят общие рёбра куба, вершины для сложных граней куба;
– имеют представление о площади поверхности куба как суммы площадей граней.
В течение 4-х лет учебы в начальной школе младшие школьники учатся распознавать геометрические фигуры на моделях, рисунках и окружающих предметах. Часть геометрического материала осознаётся детьми не на основе определений, а в результате выполнения доступных для них практических действий. Геометрические фигуры используются и во время изучения других тем, что даёт возможность широко внедрять в процесс обучения комплексные упражнения. Например, модели и изображение геометрических фигур используются как дидактический материал для изучения чисел и арифметических действий над ними; при решении задач как иллюстративный материал для формирования вычислительных навыков; для раскрытия образования частей и дробей и так далее.
Программа предусматривает овладение учащимися элементарными графическими умениями и навыками работы с чертёжными инструментами (линейкой, циркулем).
Геометрическая деятельность детей не связывается жесткой формально- логической схемой, не предлагается ученикам в готовом виде, она зарождается и систематизируется в процессе поиска, который включает в себя наблюдение, предметные действия, мысленный эксперимент. Начиная знакомство с реальных объектов и практических действий с ними, учащиеся постепенно вводятся в область идеальных конструкций и абстрактных отношений.
3. Предметные действия учащихся при изучении геометрического материала
Знакомство младших школьников с геометрическими объектами следует начинать с манипулирования реально существующими предметами, которые могут рассматриваться как модели абстрактных геометрических объектов. Именно это будет способствовать формированию адекватных перцептивных образов детей, ведь на ранних этапах наиболее эффективными и наиболее значительно влияющими на последующее развитие зрительной ориентировки являются именно виды осязания, связанные с практическим манипулированием объектами. «Рука начинает обучать глаз в процессе решения известных практических задач, связанных с захватыванием объектов и манипулированием ими». (Запорожец А.В.).
Рассмотрим различные виды предметных действий, которые осваивают ученики начальных классов в рамках изучения курса геометрии.
1). Рисование модели на бумаге при помощи различных инструментов:
а) циркуля и линейки; б) линейки и угольника; в) линейки и сетки.
Работая в тетрадях в клетку, ученики достаточно легко справляются с некоторыми построениями при помощи линейки и сетки. Например, в работе с младшими школьниками могут быть использованы упражнения, в которых требуется перенести квадрат на 2 клеточки вниз, дорисовать квадрат.
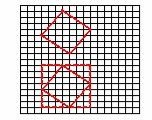
При выполнении упражнения на копирование квадрата полезно предложить учащимся проверить с помощью линейки и угольника, что данная фигура действительно является квадратом, а затем составить «маршрут» последовательного перемещения по сторонам клеток от одной вершины квадрата к другой. Этот «маршрут» можно изобразить на рисунке и записать с помощью слов (4 клетки вправо, 3 клетки вниз, 4 клетки вниз, 3 клетки влево и т. д.) или символов ( *4 – 3 ! * 4 ! 3 – * 4 – 3 ! * 4 ! 3 – ). Найденный «маршрут» поможет скопировать данный квадрат. Важно обратить внимание детей на повторяющиеся числа в записи «маршрута» и предложить им дорисовать квадрат с составлением соответствующего «маршрута».
Формированию умения у детей выполнять построения при помощи сетки
способствует использование геоплана – наглядного пособия, представляющего собой доску с набитой на ней гвоздевой сеткой (гвозди в узлах решетки).
Натягивая цветные резинки на гвозди, ребёнок получает модели различных
фигур.
2). Получение модели из бумаги при помощи перегибания
При помощи перегибания могут быть получены модели многих геометрических объектов. Применительно к получению модели ромба могут быть сформированы разные задачи. В частности, можно предложить детям получить ромб из листа бумаги произвольной формы и из прямоугольного листа. Например, берётся лист бумаги любой формы и перегибается один раз. Затем перегибается ещё раз так, чтобы первая и вторая линии сгибов образовали прямой угол. Отмечается на каждой линии сгиба по точке. Перегибается по линии, проходящей через эти точки. Лист бумаги разворачивается. Дети рассказывают о фигурах, которые получились при сгибании.
Из прямоугольного листа бумаги ромб может быть получен следующим
способом: прямоугольный лист бумаги нужно перегнуть по диагонали. Однослойные части получившейся фигуры отогнуть, накрыв ими двуслойную часть. Развернув лист бумаги, ученики рассказывают о фигурах, которые получились при сгибании.

3). Создание модели с использованием способов построений на местности
Построения на местности отличаются от построений на листе бумаги. Для
построений на местности используются различные инструменты. Они подробно описаны в некоторых пропедевтических курсах геометрии. Применительно к задачам, которые решаются в курсе геометрии, достаточно использовать колья и верёвки. Кольями отмечаются точки на местности, по верёвке, натянутой между кольями, проводятся прямые. Но так как в процессе обучения возможности для проведения реальных построений на местности ограничены, то для освоения таких построений используются листы толстого картона, имитирующие местность, булавки, имитирующие колья, и бечёвка, имитирующая верёвку.
В качестве примера рассмотрим задачу на построение на местности прямого угла. Прямой угол может быть построен на основе построения равнобедренного
треугольника (на середине бечёвки завязывается узел, который прокалывается булавкой; концы верёвки растягиваются и тоже прикалываются булавками; между этими двумя булавками натягивается бечёвка, находится её середина, прикалывается булавками; между ней и первой приколотой булавкой натягивается бечёвка – искомый перпендикуляр), ромба (верёвка с пятью равностоящими узлами замыкается в кольцо; первый и пятый узлы прикалываются булавкой; остальные узлы растягиваются и тоже прикалываются; пересекающиеся бечёвки, натянутые между первым и третьим, вторым и четвёртым узлами, образуют искомый прямой угол).
Подобные построения, проводимые под руководством учителя, способствуют накоплению у младших школьников эмпирического материала, формируются указания, в соответствии с которыми учащиеся могли бы выполнять такие построения.

4). Получение модели с использованием шнура и трубок
Использование таких моделей оказывает значительное влияние на расширение объёма изучаемых геометрических понятий за счёт простоты изменения формы. Эти модели изготавливаются из соломинок для коктейля, внутри которых располагается шляпная резинка. Вершины углов могут быть отмечены узлами или бусинами. Таким образом могут быть изготовлены модели многоугольников и многогранников. Работа школьников с моделью прямой призмы, основание которой – ромб с углом 600 , может быть связана с выполнением следующих учебных заданий: рассмотреть модель и найти известные фигуры; показать среди этих фигур одинаковые; рассказать, как узнали, что они одинаковые; выяснить, есть ли среди этих фигур квадраты; выяснить, может ли уместиться внутри этой призмы такой же квадрат; показать, как он будет расположен; выбрать, где на поверхности этой модели можно нарисовать самый длинный отрезок; рассказать, где он находится.
Наряду с описанными выше действиями с материальными моделями, которые имеют широкую область применения, в обучении учащихся можно использовать действия с предметами, приводящими к получению моделей определённого вида. В частности, наложение друг на друга полос из цветных полупрозрачных материалов позволяет получить различные виды параллелограммов; скручивание бумажной ленты (серпантин) позволяет получить модели цилиндров, кругов, конусов; определённые способы перегибания квадратного листа бумаги с последующим надуванием приводят к получению модели многогранника.
А чтобы подчеркнуть специфику геометрических объектов и сделать необходимые выводы, можно предложить учащимся написать своеобразное сочинение по геометрии, например: «Запишите все слова, которыми вы могли бы охарактеризовать куб, цилиндр, конус и т.д. Запишите слова, которые вам больше всего запомнились».
Такая форма деятельности благоприятна и для формирования геометрических представлений, и для развития речи детей.
4. Связь геометрического материала с другими предметами
Широкое использование находят геометрические образы при решении арифметических задач; сюда относится графическое изображение условия задачи, применение масштаба, связь количественных и пространственных представлений, изображений в виде отрезка расстояния между двумя пунктами в задачах на движение и др.
Существуют задачи, в которых геометрические образы выступают на первый план.
Возьмем, например, такую задачу:
Велосипедист выехал из пункта А в пункт В. Проехав 500 м, он обнаружил, что потерял ключ. Вернувшись на 100м назад, он увидел ключ на дороге. Подобрав его, он снова двинулся к пункту В и, проехав еще 800 м, достиг его. Каково расстояние между пунктами А и В?
- 500 – 100 = 400 (м)
- 400 + 800 = 1200 (м)
На уроках математики ученики могут продолжить работу над геометрическим материалом даже во время физкультминутки. Например: «Представьте себе шар, погладьте его со всех сторон. Он большой, огромный. (Ученики «обхватывают» руками и гладят воображаемый шар.) А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до вершины. (Ученики подпрыгивают.) Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, по нижнему основанию, по боковой поверхности.
Большое значение для формирования «внутреннего, смыслового» образа геометрической фигуры имеет игра «Да - нетка» или Универсальная игра для всех, в которую играют ученики разного возраста.
Эта игра способна увлечь и маленьких, и взрослых, потому что ставит учащихся в активную позицию.
«Да - нетка» учит:
- связывать разрозненные факты в единую картину;
- систематизировать уже имеющуюся информацию;
- слушать и слышать соучеников.
Учитель может «Да - нетку» использовать для создания интригующей ситуации, организации отдыха на уроке, да и не только...
Формула игры: учитель загадывает нечто (в данном случае фигуру). Ученики пытаются найти ответ, задавая вопросы. На эти вопросы учитель отвечает только словами: «да», «нет», «и да и нет». Например:
- Это фигура?
- Да.
- Эта фигура плоская?
- Нет.
- У этой фигуры есть основание?
- Да.
- Эта фигура катается?
- Да.
- У этой фигуры есть вершина?
- Да.
- Эта фигура катается только по кругу?
- Да.
- Это конус!
Как показывает практика, освоение учениками предметных и игровых действий значительно расширяет возможности учителей в организации геометрической деятельности младших школьников. Знания, полученные учениками таким образом, оказываются более прочными и качественными, обеспечивается развитие пространственного мышления, математической речи школьника, а также формируется интерес к учебному предмету.
На уроках изобразительного искусства непосредственно используются элементы геометрии. В 1-2-х классах моделями рисунков являются предметы, близкие по своей форме к простейшим геометрическим фигурам. В процессе рисования дети не только познают форму предметов, но и примерные количественные соотношения частей предметов, их взаимное расположение, направление линии.
В 3-4-х классах существенно новым является изображение тел на плоскости, причем здесь играет роль расположение предметов. Образ раскрывается с различных точек зрения. При этом дети рисуют предметы, близкие по форме к простейшим геометрическим телам: стакан, коробка, яблоко, пирамида. Учитывая это, следует устанавливать предметные связи между значениями, полученными на уроках изобразительного искусства, со знаниями, полученными при изучении начальной геометрии.
На уроках трудового обучения связь с геометрией носит действенный характер. В процессе работы над материалом (бумагой, картоном, глиной) дети моделируют геометрические фигуры и тела, познают их свойства. И если на уроках изо главную роль играли зрительные восприятия, то на уроках трудового обучения они дополняются осязанием и ощущениями при движении рук. Изготовляя изделия или детали, составляя узоры или украшения, дети сталкиваются с большим разнообразием форм. Кроме того, учащиеся учатся выполнять чертежи и технические рисунки, что имеет исключительно большое значение в геометрическом образовании. Надо заметить, что на уроках трудового обучения дети знакомятся с фигурами, которые они не изучают в курсе наглядной геометрии.
Уроки физической культуры также содержат моменты, во время которых дети пополняют геометрическое образование. Так, например, на этих уроках они получают ориентировку в направлении: направо, налево, вверх, вниз в горизонтальном и вертикальном положении, в построении по прямой линии, в круг, по границе участков в форме прямоугольника, квадрата, в поворотах на прямой, развернутый, полный угол.
На уроках русского языка учащиеся встречаются с выражениями о направлении, форме предметов, об их взаимном расположении.
Способствует развитию речи учеников работа по сочинению сказок о геометрических фигурах.
Вот некоторые из них.
В некотором царстве, в математическом государстве, в городе Геометрия поспорили прямоугольник и квадрат, кто из них важнее.
- Я важнее, - говорит прямоугольник, - потому что у меня целых 4 вершины.
- Неправда, я важнее, это у меня 4 вершины, - возразил квадрат.
Прямоугольник удивился, но вынужден был согласиться, когда насчитал у квадрата тоже 4 вершины.
- Зато у меня 4 стороны, - гордо заявил прямоугольник.
- И у меня 4, - невозмутимо парировал квадрат.
- А у меня все углы прямые, - рассердился прямоугольник.
- Хоть сердись, хоть нет, но и у меня все углы тоже прямые, - не отступал квадрат.
- А у меня, - не унимался прямоугольник, - противоположные стороны равны.
- И у меня противоположные стороны равны, - продолжал настаивать квадрат.
- Тогда почему же мы не похожи друг на друга, если у нас так много общего? – просил прямоугольник.
- Давай-ка спросим у хозяйки тетради, в которой мы живем, - предложил квадрат.
Побежали они к девочке.
- Рассуди, кто из нас важнее, если у нас обоих по 4 вершины, по 4 угла и все они прямые, по 4 стороны, где противоположные из них равны.
- Не ссорьтесь, вы все сказали правильно, кроме одного: квадрат – это прямоугольник, у которого все стороны равны, а у прямоугольника равны только противоположные стороны. Поэтому вы так похожи и не похожи одновременно, но оба вы очень важны для города Геометрия.
Успокоились прямоугольник и квадрат, помирились да так и остались жить в математическом государстве.
И я там был, спор слышал, участия в нем не принимал, но вывод для себя сделал.
**********************************************************************
Стороны квадрата а и b болтали, сидя на трубе. Вдруг а упала, а b тотчас запричитала:
- Ах я бедная, несчастная, осталась совсем одинокая. Не с кем теперь поболтать, не с кем периметр квадрата посчитать.
Пробегала мимо Геометрия, услышала эти причитания, остановилась и сказала:
- Прекрати истерику. Я уверена, что сторона а специально упала, чтобы проверить твои знания о квадрате и удостовериться , что ты сможешь и без нее посчитать периметр квадрата.
Задумалась b.
- А и правда, попробую сама посчитать периметр квадрата. Сколько всего сторон у квадрата? Четыре. А что я знаю о его сторонах? Они все равны. А что это значит? Это значит, что сторона b, то есть я, равна стороне а. Сколько всего сторон а? Две. А сторон b? Тоже две. Тогда получается, что периметр квадрата равен а + а + b + b ? Ура! Молодец я! Смогла и без а посчитать периметр квадрата.
Тут, откуда ни возьмись, появилась а:
- Молодец-то, молодец. Но со мной все-таки веселее: можно вместе и поболтать и периметр посчитать.
Взялись а и b за руки и побежали вприпрыжку, радуясь тому, что они снова вместе.
********************************************************************************
... И очутился Кай перед злющей-презлющей королевой-матерью Вьюгой вьюжной. Стукнула она своей ледяной палицей, чтобы еще больше запугать мальчика, и сказала:
- Ты должен раскрыть мне секрет, как построить вокруг замка красивое ограждение из тончайших ледяных пластинок прямоугольной формы со сторонами а и b, используя разные способы вычисления периметра этих пластинок.
- Но я не знаю никакого секрета, - робко возразил Кай.
- Ничего не желаю слышать, - грозно произнесла Вьюга. – Не знаешь, значит узнай. Да, и еще. Способов вычисления периметра должно быть четыре. Если хотя бы один не назовешь, ты навсегда останешься в моем королевстве и никогда не вернешься домой.
Стал Кай вспоминать все, что он знал о прямоугольниках. И вдруг, о радость, он вспомнил, что действительно есть разные способы вычисления периметра.
- Ура! – закричал Кай и, еле дождавшись рассвета, побежал к Вьюге.
- Я выполнил твое задание! – сообщил он с порога. – Теперь ты должна отпустить меня домой.
- Сначала докажи, что ты справился с приказом, - недовольно заметила Вьюга.
- Смотри, как все просто. У прямоугольника две стороны а и две стороны b. Периметр его равен сумме всех четырех сторон, а это значит а + а + b + b.
- Это первый способ вычисления периметра, а где еще три?
- Второй: а + b + а +b; третий: а 2 + b 2; четвертый: (а + b) 2, - выпалил Кай.
- Да, ты, я вижу, хорошо выучил геометрический материал. Делать нечего, придется тебя отпустить.
Кай стремительно выскочил из замка и быстро скрылся из виду.
5. Иллюстративная роль геометрических образов при обучении математике
Числовые понятия в раннем детстве образуются путем созерцания групп предметов и поэтому в этот период бывают еще связаны с групповыми образами. Ребенок думает, например, о числе четыре.
Каждую группу можно представить составленной из более мелких подгрупп. Например, четыре ноги животного – из двух ног впереди и двух сзади. Таким образом возникают понятия о составе числа, в данном примере о составе четырех из двух и двух.
Для лучшего усвоения состава числа дети пользуются числовыми фигурами. Нарисовав у себя «рамочки» заданных размеров, вписывают в них точки.

Получаются таким образом числовые фигуры. Точки дети считают так: «По две точки два раза – два, четыре. По две точки три раза – два, четыре, шесть. По две точки четыре раза – два, четыре, шесть, восемь» и т.д.
Дополнение одного числа до другого можно выполнить тоже с помощью числовой фигуры. Например:


х + 4 = 7 4 + х = 7
Сколько точек надо добавить до четырех точек, чтобы получилось семь?
Для развития беглости вычисления надо научить детей пользоваться магическими квадратами, которые дети зарисовывают у себя в тетрадях. «Магические» свойства квадратов заключается в том, что суммы чисел, расположенных в рядах, столбиках и по диагоналям, равны. В последние два квадрата надо вставить цифры так, чтобы квадраты приобрели «магические» свойства.
|
8 |
3 |
4 |
|
5 |
10 |
3 |
|
6 |
1 |
|
|
1 |
5 |
9 |
|
4 |
|
|
|
7 |
5 |
|
|
6 |
7 |
2 |
|
|
|
7 |
|
2 |
|
|
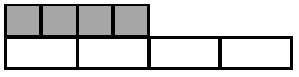
Состав чисел второго десятка и данного числа единиц удобно иллюстрировать группами квадратов.
Десяток берется в виде бумажной полосы, разделенной на 10 квадратов. К этой полосе справа прикладывается 1, 2, 3 и т.д. квадратов.
Подобная же фигура может служить образом для пояснения сложения и вычитания с переходом через десяток. Например, 7 + 5 = (7 + 3) + 2. Группы 7 и 5 квадратов берутся разных цветов.
При прохождении дробей доли единицы могут иллюстрироваться разными легко делимыми предметами.
![]()



![]()
![]()
![]()

![]()
![]()
![]()
Образы дроби ¾
6. Фрагменты уроков с использованием геометрического материала
и комментарии к ним
|
Еще до школы практически все дети знакомятся с такими геометрическими фигурами как круг, квадрат, треугольник, прямоугольник, овал. С ними же они сталкиваются и на уроках математики. Учителю необходимо использовать каждую ситуацию, когда дети в своей речи используют слова «кружок», «квадратик» и т.п., для замещения этих названий математическими «круг», «квадрат», «треугольник». Также важно, чтобы учитель следил и за собственной речью – не говорил: «Нарисуйте три кружка...». Дети постепенно овладеют правильной терминологией. Предлагаем вашему вниманию фрагмент урока, на котором учитель правильно построил работу по уточнению терминологии. На доске плакат с изображениями круга и треугольника. Учитель. Кто назовет эти фигуры? Саша. Здесь кружок и треугольник. У. Все согласны с Сашей? Дети. Да! Да! У. Саша, повтори, пожалуйста, названия этих фигур, а вы слушайте внимательно. Саша повторяет слова кружок и треугольник. – Что-нибудь заметили? Дети молчат. – Тогда послушайте еще раз. Учитель сам произносит слова кружок, треугольник, выделяя голосом вторую половину первого слова. Оля. Я заметила! «Кружок» – так в детском саду говорят, а в школе – «круг»! Все дети оживились, улыбаются. У. Молодцы, я вижу, вы все согласны, поняли, что Оля правильно сказала. Но эту фигуру так называют не только в школе – так ее называют в науке математике даже самые знаменитые ученые. Дети сравнивают круг и треугольник и начинают выполнять задание, в котором нужно сравнить два множества деревьев. У. Как узнать, каких деревьев больше, а каких меньше? Люба. Их нужно соединить парами. У. Как? Люба. Соединить линиями. У. Я согласна, но так мы уже делали не раз. Есть еще предложения? Дети молчат. – Тогда я вам помогу. Достаньте из своих касс кружки и квадратики (учитель не очень заметно, но подчеркивает голосом эти слова). В классе движение, многие поднимают руки. – Что такое, вы уже догадались, что я хочу сказать? Петя (хитрым голосом). Нет. Но вы сказали – «кружки и квадратики»! Разве математики так говорят? Все дети смеются, учитель тоже. У. Какие же вы у меня молодцы, не дали себя перехитрить, заметили! Как же правильно нужно сказать? Д. (хором). Круги и квадраты! Сравнивая знакомые фигуры между собой, дети начинают осознавать, в чем заключается сходство и различие фигур. Так, они замечают, что в треугольнике меньше сторон и углов, чем в квадрате. Уже на этом этапе дети устанавливают связь между названием «треугольник» и числом углов в этой фигуре. После установления связи между названием и числом углов треугольника необходимо продолжить эту линию и предложить детям дать другое название квадрату. Однако переключение со знакомого, привычного названия фигуры на новое может оказаться для учеников слишком трудным. В этом случае выйти на термин «четырехугольник» можно при рассмотрении произвольного четырехугольника, а затем подвести под этот термин и такие знакомые фигуры, как квадрат и прямоугольник.
Приведенная выше работа подготавливает почву для решения одного из важных аспектов решения второй задачи – формирования общего способа классификации многоугольников по числу углов. Предлагая регулярно для рассмотрения многоугольники с различным количеством углов, помогая детям найти их названия, учитель продвигает детей в осознании этого способа классификации. Приведем соответствующий фрагмент урока. Учитель. Как называется многоугольник, начерченный на доске? Открыта небольшая часть доски с изображением произвольного треугольника. Дети. Это треугольник. У. Почему он так называется? Д. Он так называется потому, что у него три угла. – А еще у него три стороны. У. Начертите в тетради любой треугольник. Дети чертят в тетрадях разные треугольники. – Поменяйтесь тетрадями и проверьте работы друг друга. Дети выполняют проверку, ошибок нет ни у кого. – А теперь посмотрите на новый чертеж на доске. Как бы вы назвали этот многоугольник? Учитель открывает следующую часть доски.
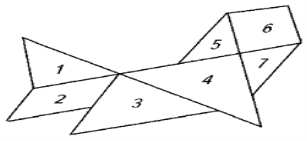
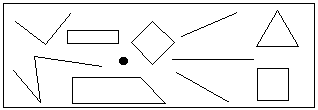
Рисунок. Д. Это, наверное, четырехугольник. – Конечно, четырехугольник – у него ведь четыре угла! – Я согласна с таким названием. У этого многоугольника четыре угла и четыре стороны, значит, это четырехугольник. У. А теперь рассмотрите новый чертеж и назовите сначала номера всех треугольников, а потом всех четырехугольников.
Рисунок. Дети выполняют задание достаточно успешно: номера треугольников все назвали верно, затруднения возникли только в работе с невыпуклым четырехугольником. – Теперь рассмотрите внимательно те многоугольники, номера которых вы не назвали, и объясните, почему так получилось. Д. У фигуры под номером 3 целых 6 углов и 6 сторон.
– А у восьмой фигуры – 5 углов и 5 сторон, это тоже не треугольник и не четырехугольник. – Нет, я с Настей не согласен – ведь у фигуры есть и углы, и стороны. Это какой-то угольник, только необыкновенный. – Я тоже думаю, что это какой-то угольник, и если посчитать его углы и стороны, то это четырехугольник. У. Ребята, кто же прав? Большая часть учеников, подумав, соглашается с тем, что это тоже четырехугольник. Но довольно большая группа с этим не согласна. – Мы с вами еще не раз будем рассматривать такие фигуры, а сейчас подумайте, как вы назовете многоугольники под номерами 3 и 8.
Д. Многоугольник под номером 3 – это шестиугольник: у него 6 углов и 6 сторон. У. Молодцы, вы очень хорошо работали с многоугольниками. Параллельно с этим происходит и подведение под общее понятие различных фигур, то есть установление связи род – вид. Основные линии этой работы можно проследить в приводимом ниже фрагменте урока. На доске прикреплены плакаты с пятиугольником, четырехугольником и шестиугольником произвольной формы. Учитель. Рассмотрите внимательно эти фигуры. Чем они похожи? Чем различаются? Дети отмечают, что сходство в том, что все они составлены из отрезков и имеют углы. Отличаются же они количеством углов и отрезков. Сравнивая фигуры, дети свободно называют каждую из них – пятиугольник, четырехугольник, шестиугольник – и объясняют эти названия без побуждений со стороны учителя. – Хорошо, вы все правильно сказали и многое заметили. А теперь я задам вам трудный вопрос: как можно назвать все эти фигуры одним общим словом? Маша (очень неуверенно и после продолжительной паузы). Может быть, назвать их «угольники»? Ведь у них у всех есть углы. У. Хорошо, Маша. Кто еще предложит свое название? Дима. Я думаю, Маша правильно говорит. В названии обязательно должно быть «угольники», ведь все так называются – «треугольники», «четырехугольники» (голосом выделяет общую часть), только что-то нужно добавить. Я думаю, можно назвать «разноугольники». У. Ребята, вам нравится Димино название? Дети. Да, нравится, он правильно придумал. У. Да, Дима, твое название хорошее, оно мне тоже очень нравится. А сейчас я вам скажу, как математики называют все эти фигуры, – это многоугольники. Ира. А я слышала это слово! Мой брат, он в седьмом классе учится, все говорил – «многоугольники», «многоугольники», а я и не знала, что это такое. У. Вот видите, какие вы уже большие и умные, только в первом классе учитесь – и тоже узнали, что такое многоугольники. А теперь подумайте, почему эти фигуры называют многоугольниками? Алеша. Ну, наверно, потому, что у них много углов. Юра. Разве четыре – много? Вот если сто, тогда много! Просто углов сколько угодно может быть, вот так и назвали, не придумали лучше. Дима лучше назвал! Вот и нужно этим математикам написать. Миша. Мне тоже Димино название нравится, оно точнее. У. Хорошо, мы можем написать письмо, но пока давайте называть фигуры так, как их называют в математике. Да и слово не такое уж неудачное, ведь здесь много – значит неизвестно сколько, но не один угол. Ведь и два по сравнению с одним – уже много, правда? Затем учитель показывает различные фигуры, а дети устанавливают, относится ли каждая из них к многоугольникам или нет: среди фигур, кроме различных многоугольников, находятся круг, отрезок, угол, сектор. Ученики дают обоснованные ответы. С первых уроков начинается знакомство с простейшими геометрическими фигурами – точкой и линией – на уровне наглядного восприятия моделей этих фигур как в виде изображения их на чертеже, так и в качестве элементов реальных объектов, окружающих детей. Рассмотрим фрагмент урока в 1-м классе, посвященного знакомству с точками и линиями. Учитель. Откройте свои маленькие тетрадки на чистой странице и возьмите простые карандаши. Прикоснитесь к бумаге карандашом. Кто скажет, что у вас получилось? Дети. Я знаю, у меня получилась точечка! – А у меня – маленькая закорючка, точка с хвостиком. – Это неправильно, ты карандаш двигал, вот и получился хвостик. – А называть надо не «точечка», а точка. – Откуда ты знаешь, как нужно называть? – Я от сестры слышала, у нее такой урок есть – геометрия. У. Юля правильно говорит. Если вы только прикоснулись к бумаге карандашом, у вас получилась точка. Поставьте на листочке еще одну точку. Дети ставят в тетрадях еще точки. Некоторые подзывают учительницу и просят разрешения поставить еще точку, так как вторая точка не получилась. – А теперь сделайте так: поставьте точку и от нее двигайте карандаш туда, куда вам хочется. Дети выполняют задание. – Что у вас получилось теперь? Д. У меня получилась полоска с точкой на конце. – Это точка с хвостом. – Мне кажется, это называется «линейка». – Нет, линейка вот какая, а это, наверное, линия.
У. Молодец, Костя, ты правильно назвал получившиеся фигуры. Найди на чертеже похожие линии. Обведи линии каждой группы одним цветом. Для линий разных групп используй разные цвета.
Рисунок. Рассмотри линии. В математике их называют прямые.
Рисунок. Прямые чертят с помощью линейки. Дано изображение линейки без делений. Начерти несколько прямых. На каждой прямой линии поставь точку.
Рисунок. Как бы ты назвал линии, на которых ты не ставил точки? В математике эти линии называются кривые. Тебе нравится это название? Почему их так назвали? Начерти несколько прямых и кривых линий. Прямые черти красным карандашом, кривые – простым. Чтобы ученики представили себе такое понятие, как бесконечность прямой, предлагается сначала использовать такую практическую работу: как можно более длинные, толстые и яркие нитки наматывают примерно поровну на 2 катушки. Учитель дает по одной катушке двум ученикам, они становятся лицом друг к другу, туго натягивая разделяющую их часть нитки. По команде учителя дети начинают медленно расходиться в противоположные стороны, разматывая натянутую нитку. Если у кого-то из детей кончается нитка, но есть место для продолжения движения, можно привязать дополнительный кусок нитки, но можно этого и не делать. После завершения практической работы необходимо обсудить с детьми причины, по которым им пришлось остановиться, и что можно было сделать, чтобы продолжить движение. Таких причин две:
– закончилась нитка, и в этом случае поможет увеличение длины нитки; В процессе деятельности учитель задает следующие вопросы: какая получилась линия? Можно ее продолжить? Как это сделать? Дети с катушками расходятся до тех пор, пока не дойдут до стен класса. Можно вывести детей в коридор и там продолжить разматывание нити. В качестве следующего шага можно использовать такой прием: на доске чертится часть прямой. Учитель спрашивает, можно ли эту прямую продолжить, сделать длиннее. Возможно, дети сразу догадаются, что можно. Если такой ответ получен, нужно предложить рассказать, как это можно сделать (приложить линейку к части начерченной линии и начертить дальше). Учитель выполняет эту операцию и спрашивает, можно ли еще продолжить эту прямую. Постепенно прямая продолжается до краев доски. А дальше можно? Очевидно, дети скажут, что дальше чертить нельзя. На этом этапе устанавливается, что причина не в том, что прямая не может продолжаться, а в том, что кончилась доска. Дальше учитель предлагает детям представить, какой длины можно было бы начертить прямую, если ее чертить не на доске, а на стене, на полу класса, в коридоре, на земле во дворе и т.д. Так постепенно у учащихся формируется понимание возможности неограниченного продолжения прямой. После знакомства с прямой рассматривают фигуры, которые являются ее частями: луч и отрезок. Прямую, луч и отрезок сравнивают между собой, устанавливают отличие луча от отрезка и от прямой. При знакомстве с отрезком основное внимание уделяется его ограниченности с двух сторон, а луча – с одной стороны. Можно использовать такой вариант знакомства с отрезком: на доске изображаются две точки. Затем формулируется задание: соединить точки линией. Учитель не должен торопиться с разъяснениями – нужно предоставить ученикам время для самостоятельного выполнения задания. Только после этого несколько учеников показывают на доске свои решения, используя одну и ту же пару точек. На доске получается чертеж, на котором две точки соединены несколькими разными линиями. Очень важно так подобрать решения детей, чтобы были выявлены все допущенные ошибки (например, вместо того чтобы соединить точки линией, ученик проводит линию через две точки, то есть концы линии не находятся в данных точках) и были представлены все принципиально разные варианты решений. Если среди них будет отрезок, учителю останется только сконцентрировать внимание учеников на этом решении, выделив его среди других, что нетрудно сделать, так как все остальные решения, очевидно, будут кривыми линиями. Кроме того, дети легко заметят, что эта линия является самой короткой. Если среди предложенных детьми решений отрезка не окажется, учитель предлагает выполнить такое задание. Соедини точки при помощи линейки.
Рисунок. У тебя получился отрезок. Научись правильно чертить отрезки.
Рисунок. Начерти несколько отрезков.
Затем сравнивают отрезок и прямую и устанавливают ограниченность отрезка. Отрезок имеет два конца (могут быть использованы и названия начало и конец отрезка). Сравни линии. Чем они похожи? Чем отличаются? Рисунок. На рисунке прямая, отрезок и луч. Названия каких из этих линий ты знаешь? Обведи их зеленым карандашом. Линия на этом рисунке называется луч. Рисунок. Произвольно расположенный луч. Найди на верхнем рисунке луч, обведи его красным карандашом. Объясни, чем луч отличается от прямой. А от отрезка? Начерти два луча. Дальнейшее продвижение в знакомстве с геометрическим материалом тесно связано с взаимным расположением различных линий, особенно прямых, лучей и отрезков, что приводит к знакомству с различными новыми геометрическими фигурами (углами, ломаными линиями, многоугольниками и т.д.). Весь остальной геометрический материал изучается аналогично, начиная с основополагающего понятия и постепенно расширяя и углубляя тему. Такое построение материала является второй особенностью изучения элементов геометрии, хотя относится не только к нему. Одним из важных направлений изучения элементов геометрии в начальной школе, начиная с 1-го класса, является работа с объемными телами (как в виде реальных предметов, окружающих учеников в трехмерном пространстве, в котором они существуют, так и в виде моделей пространственных фигур – цилиндра, конуса, шара, призмы, пирамиды). Первые два года обучения младшие школьники работают только с реальными объемными предметами и моделями основных объемных фигур – шарами, цилиндрами, конусами, призмами и пирамидами. При изучении темы работа ведется в следующих направлениях: – сравнение различных реальных предметов и выделение групп предметов, сходных по форме. Например, может быть предложен такой набор: мяч, банка, круглый карандаш, яблоко, кусок трубы, круглый воздушный шар. Их нужно разделить на две группы по какому-либо признаку. Среди предложенных решений (а их может быть много, так как дети могут ориентироваться на разные признаки – размер, массу, цвет, прозрачность и т.д.) учитель обращает особое внимание учеников на вариант, когда предметы объединены по форме. Такое предпочтение легко может быть оправдано тем, что при занятиях геометрией всегда большое внимание уделяется именно форме рассматриваемых фигур; – подбор других подходящих по форме предметов к выделенным группам. Эта часть работы может происходить в классе с реальным набором предметов или с их названиями, либо может быть дана в качестве домашнего поручения – найти подходящие по форме предметы среди игрушек или предметов домашнего обихода; – сравнение выделенных по сходству формы предметов с моделями объемных геометрических фигур и выбор соответствующих моделей, знакомство с названиями выбранных моделей. Так, в результате выполнения задания, приведенного выше, дети выделят две группы вещей, сходных по форме: мяч, яблоко и воздушный шар; банка, карандаш, труба. Учитель показывает несколько моделей – конус, шар, призму, цилиндр – и предлагает выбрать те, которые по форме больше всего подходят к выделенным группам. Очевидно, дети без труда идентифицируют с ними шар и цилиндр, после чего вводятся названия соответствующих геометрических фигур – шар, цилиндр. Как и всегда, прежде чем сообщить названия выбранных моделей, необходимо поинтересоваться, не знает ли их кто-нибудь из учеников. Если окажется, что это так, то названия (или одно из них) сообщает не учитель, а дети; – выделение знакомых плоскостных фигур на поверхности объемных. Это направление позволит связать в единое целое объемные и плоскостные фигуры, где плоскостные фигуры выступят в своей естественной для трехмерного пространства роли – части объемного тела (например, круг выступит как часть поверхности конуса или цилиндра, прямоугольник – как часть поверхности призмы, треугольник – пирамиды и т.д.); – выделение из реальных предметов сложной формы частей, имеющих форму шара, цилиндра, конуса, призмы, пирамиды; – создание моделей объемных фигур из пластилина и композиций из этих моделей. Это направление может осуществляться не только на уроках математики, трудового обучения, но и дома. Желательно, чтобы для создания сложных композиций моделей дети объединялись в группы. Это позволит по-разному организовать работу начиная с варианта, когда у учеников уже есть готовые вылепленные модели и группа придумывает возможную для этого набора композицию, и заканчивая случаем, когда сначала группа придумывает композицию, определяет, какие, сколько и какого размера нужно вылепить модели для ее осуществления, распределяет их изготовление между участниками и создает задуманную композицию. В 3-4-м классах дети знакомятся с различными приемами изображения на плоскости объемных предметов, создающих иллюзию объемности. Через систему заданий дети самостоятельно подходят к выводу о том, что для этого используют художники, графики, чертежники. (Художники-живописцы используют для этого игру светотени или перспективу, графики – искривление линий, чертежники –проекцию). Помимо этих приемов, дети знакомятся с изображением трех видов объекта (спереди, сверху, сбоку). Этот способ особенно важен для развития пространственного воображения. Новое направление в рассмотрении объемных фигур – сравнение моделей различных наименований. Весь данный материал изучается на ознакомительном уровне. Например, сравнивая модели шара, цилиндра, конуса, дети отмечают, что общее для них – это способность к качению (катится). Различие в том, что шар катится произвольно, цилиндр – по прямой, конус – по кругу, в центре которого находится его вершина. Различия этих тел также в том, что у шара нет ни вершин, ни оснований, у цилиндра – два основания, но нет вершин, у конуса – одно основание и одна вершина. Аналогично рассматриваются и сравниваются призма и пирамида, цилиндр и призма, пирамида и конус и т.д. Вариантом такой работы является сравнение объемных фигур одного наименования. Например, детям предлагается сравнить несколько разных призм. При выполнении задания выявляются признаки сходства и различия.
Заключение. Итак, как видим, на уроках в начальной школе, где изучается геометрический материал можно широко применять продуктивные методики и технологии обучения, которые формируют и развивают группы ключевых компетентностей учащихся. Потенциал продуктивных методик очень высок, реализация его непосредственным образом влияет на достижение такого результата обучения как компетентность. |
Подводя итог сказанному, надо отметить, что геометрия действительно занимает большое место в жизни человека, она действительно находится вокруг нас. Не может не видеть этого только слепой.
Поэтому кому, как ни учителю начальной школы, нужно заинтересовать ученика изучением науки, которая стояла еще у колыбели человеческого разума и которая может и сегодня помочь человеку сделать еще один скачок в своем развитии. Интеллектуальном, духовном и нравственном. Ведь геометрия обладает большими возможностями в формировании жизненных и ключевых компетентностей человека. Надо просто не упустить эту возможность.
- РАЗРАБОТКИ УРОКОВ, НА КОТОРЫХ ИЗУЧАЕТСЯ
ГЕОМЕТРИЧЕСКИЙ МАТЕРИАЛ
Тема. «Ломаная» (первый урок).
Цели. Познакомить с новой линией; совершенствовать умения сравнения и классификации геометрических фигур; учить планировать деятельность, проводить самооценку своих действий.
Оборудование. Учебник «Математика. 1-й класс»; тетрадь на печатной основе; листочки с заданиями.
ХОД УРОКА
I. Организационный момент
II. Актуализация знаний
На доске чертеж. У детей на столах листочки с таким же чертежом.
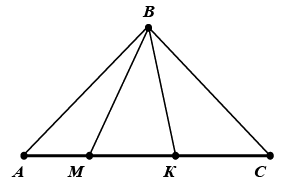
Учитель. Сколько отрезков вы видите на чертеже?
Дети отвечают.
– Кто согласен?
Ученик у доски показывает отрезки, а дети считают и дополняют при необходимости.
– Какие отрезки нужно сложить, чтобы получился отрезок АС?
Дети отвечают и показывают у доски свой вариант ответа.
– Кто согласен?
Выслушиваются ответы детей.
– Найдите сумму отрезков АВ, ВK и KС. Как будем действовать?
У доски работает ученик и комментирует все свои действия.
– На ваших чертежах отрезок, равный сумме отрезков АВ, ВK и KС, выделите синим цветом.
Аналогичное задание выполняется у доски.
– С какими линиями мы сейчас работали?
Дети отвечают.
III. Знакомство с новым материалом
У. Прочитайте тему урока.
Дети. Ломаная.
У. Подумайте, чему мы будем учиться?
Выслушиваются ответы детей.
– Ломаная – это особая линия. Мы будем учиться чертить такие линии, узнаем, как называются ее части, и попробуем сравнивать ломаные по длине.
На доске:

– Откройте задание. Что нарисовано?
Д. Линии.
У. Чем похожи эти линии? Чем они различаются? Начертите по линейке отрезок АВ и линию ВМ.
Дети чертят отрезок АВ из 5 частей и ломаную ВМ из 5 частей (звеньев).
– Как вы думаете, какая линия длиннее? Обсудите это в парах. Чья пара поделится своим секретом?
Выслушиваются ответы. Дети сравнивают длины отрезка и ломаной.
– Какие еще линии мы сегодня не изображали?
Д. Кривые, прямые.
У. Прочитайте задание.
Д. «Назови лишнюю фигуру».
У. Как вы ответите?
Д. Лишняя – ломаная, так как остальные – кривые.
– Лишняя – синяя кривая, так как остальные – красные.
У. Знаете ли вы, как называются части (кусочки) ломаной?
Выслушиваются ответы детей.
– Часть ломаной называется звено. Сосчитайте звенья красной ломаной линии. Вспомните состав числа 6. Запишите в тетрадь. Что у вас получилось?
Д.

У. Откройте тетради на печатной основе, найдите задание. Что нас просят сделать?
Д. Сравнить числа и выражения.
6 * 8 7 * 8 9 * 6
2 + 4 * 5 + 3
4 + 3 * 7 + 1
6 + 3 * 3 + 3
Дети работают самостоятельно.
IV. Закрепление изученного
У. Прочитайте задание 29 в тетради. Сколько звеньев (частей) будет у ломаной? О чем нам здесь нужно помнить?
Д. Звенья не должны пересекаться.
У. Сосчитайте количество звеньев. Что у вас получилось?
Дети отвечают.
V. Итог урока
У. О чем вы узнали на уроке?
Какое самое маленькое число звеньев может быть в ломаной?
Начертите такую ломаную в тетради.
Вспомните, как можно сравнить длины отрезка и ломаной.
Дети отвечают.
|
Тема. «Плоскостное моделирование. Аппликация “Кораблик”».
Форма урока. Игра-путешествие «По морям, по волнам». Цели. Познакомить учащихся с видами водного транспорта, его назначением; закреплять навыки работы с бумагой, умение выполнять аппликационные работы; способствовать развитию у детей глазомера, понимания соотношения частей и целого, понимания цвета. Оборудование. Цветная бумага, ножницы, клей, кисточки для клея, подставки для кисточек, тряпочки, подкладной картон, клеенка; рисунки морских судов, маяка, капитана; карточки для игры «Капитаны», бинокль; раздаточные листы с образцом кораблика, логические квадраты, памятки по работе с ножницами, клеем и кисточкой; магнитофон, аудиозаписи песен «Капитан, капитан, улыбнитесь!», «Мы пришли сегодня в порт»; книги: С. Сахаров – «История корабля»; В. Маяковский – «Эта книжечка моя про моря и про маяк»; А. Беслик – «Поднять паруса!»; комплект открыток «История корабля». ХОД УРОКА I. Организационный моментУчащиеся класса разделены на группы по 4 человека. Учитель.
Дополнительный дан звонок – II. Сообщение темы урокаУ. Отгадайте загадки:
На море, в реках и озерах Дети. Катер. У.
Не спрашивая броду, Д. Теплоход. У.
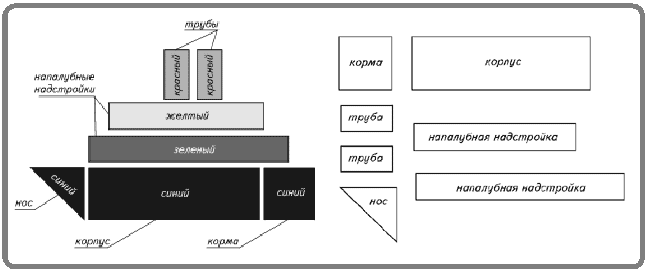
Под водой – железный кит. Д. Подводная лодка. Учитель располагает на доске рисунки с видами транспорта, угаданными детьми. У. Как можно назвать одним словом катер, теплоход и подводную лодку? Д. Это водный транспорт. У. Какие еще виды водного транспорта мы знаем? Дети отвечают. У. Итак, мы начинаем путешествие по волнам, по морям на нашем кораблике. Учитель показывает изображение кораблика на классной доске.
– Проверьте, у вас на партах должно быть все необходимое для работы: цветная бумага, ножницы, клей, кисть для клея, подставка под кисть, тряпочка, подкладной картон, клеенка. Д. Он должен быть умным, собранным, требовательным, уметь доводить дело до конца. Учитель показывает образец аппликации «Кораблик».
У. И вам, чтобы выполнить эту работу, необходимы будут внимательность, аккуратность и старание. Название нашей аппликации – «Кораблик». На нем мы и совершим свое путешествие. III. Вводная беседаУ. Никто не знает, когда и как впервые человек поплыл по воде. Уже много лет тому назад люди стали использовать для передвижения водоемы. Они научились переплывать реки, преодолевать озера, перебираться с острова на остров. Жители разных стран научились строить лодки, выдалбливая их из стволов деревьев, сшивая из их коры. Учитель показывает рисунки из книги С. Сахарова «История корабля». – Плавали и на надутых шкурах. Затем появились плоты, первые корабли – кочи, ладьи, торговые и военные суда, пароходы, теплоходы. IV. Игра «Капитаны»У.
Почему пароход не садится на мель, Д. Математика. Слева на доске – рисунки пароходов. Справа – ряд карточек с цифрами 1, 2, 3, 4, 5 ... 10 – это «пристани». Курс каждого парохода зашифрован примером, а место на пристани – номером. У. Каждый капитан должен определить курс движения (решить пример), а потом поставить свой пароход на место. Кто раньше всех причалит к берегу, тот станет лучшим капитаном, который затем и поведет нас дальше в путешествие. Капитаны команд решают примеры и закрепляют рисунки под цифрами, совпадающими с ответами примеров. Определяется лучший капитан. – Многое должен знать капитан, чтобы идти намеченным курсом. Представим, что на море шторм, высокие волны, а корабль качает из стороны в сторону. Любая ошибка в расчетах потопит его, погибнут люди.
Капитан берет бинокль V. Подготовительная работа. Анализ конструкции изделияУ. Что же делать? Как же быть? Надеваем спасательные круги (показ рисунка) и добираемся до острова Геометрии. Может быть, на нем мы сможем собрать новый корабль. Мы добрались до острова, нас встречают его жители. Они нам помогут, если мы выполним все их задания. Задание 1У. Назовите знакомые вам геометрические фигуры. На доске нарисованы или вывешены изображения геометрических фигур: круг, квадрат, трапеция, треугольник, прямоугольник, ромб. Задание 2У. Какие геометрические фигуры использованы в аппликации? Задание 3У. Назовите каждую часть корабля. Д. Корпус, нос, корма, надпалубные настройки, трубы. Задание 4У. Определите цвет и форму корпуса, носа, кормы, надпалубных надстроек и труб. Д. Прямоугольники, квадраты, треугольник. У. Какой вид бумаги мы используем для работы? Д. Цветную бумагу. VI. Игра «Логический квадрат»У. Жители острова Геометрии дарят нам яхту (показ рисунка), но она слишком мала для дальнейшего путешествия. На ней мы сможем добраться лишь до бухты Верный Друг, где и начнем строительство нашего корабля.
Якоря кругом сверкают – Учитель показывает рисунки капитана и яхты на доске.
Весьма опасен остров Рыбы:
Логический квадрат разобран на 7 частей. Из них нужно сложить остров Рыбы. Бухта Верный Друг – ее образуют 3 линии. Команды выкладывают остров Рыбы у себя на партах. VII. Практическая работаУ. Вот и бухта. Можно передохнуть. Вырежем по контуру все части корабля. А выполнить операцию вырезания помогут ножницы-художницы, которые покажут нам свои приемы. Вспомните приемы резания ножницами, технику безопасной работы с ними.
– Итак, начинаем вырезать по порядку: 1) корпус; 2) корма; 3) нос; 4) надпалубные надстройки; 5) трубы. Во время работы звучит песня «Капитан, капитан, улыбнитесь!». – Довести дело до конца нам помогут кисточка и клей. Но и здесь нам необходимо вспомнить правила работы с ними.
У. Старайтесь. Не спешите. Поспешишь – людей насмешишь.
Дети наклеивают детали. – Корабли собраны. Что происходит?
Вдруг – обрадован моряк: Каких только кораблей и судов нет в нашей бухте!
Волны, как теперь ни ухайте, – Учитель показывает иллюстрации с изображениями морских судов: рефрижератор, траулер, научно-исследовательский корабль, грузовой экспресс, рудовоз, спасатель, супертанкер, автовоз, лесовоз, плавзавод, сухогруз, танкер, теплоход, филейный траулер, китобоец, суперлайнер, китобаза и др. VIII. Уборка рабочих местЗвучит мелодия песни «Мы пришли сегодня в порт». У. Капитаны привели свои корабли в назначенное место. Дело сделано, и нам тоже осталось довести дело до конца и привести в порядок свое рабочее место. |
||||||||||
|
Тема. "Прямоугольник и квадрат".
Цели. Сформировать у детей представления о существенных признаках прямоугольника и квадрата, ориентируясь на которые они могли бы распознать эти фигуры; развивать умения наблюдать и сравнивать. Оборудование. Индивидуальные доски для отвечающих у доски учеников; комплекты геометрических фигур для всего класса; угольники; рисунки геометрических фигур для иллюстрирования геометрической сказки.
ХОД УРОКА I. Организационный моментII. Мобилизующий этапУчитель. Посмотрите на чертеж на доске. На доске:
– Какие фигуры вы нашли? Дети. Треугольники и четырехугольник. Дети выходят к доске и показывают найденные фигуры на чертеже. У. Дайте определение треугольника. Д. Геометрическая фигура, у которой три стороны, три угла, три вершины. У. Сколько на чертеже треугольников? Д. Восемь.
У. Молодцы. Сегодня на уроке нас ожидает встреча с удивительной наукой – геометрией. III. Арифметический диктантДети записывают ответы в тетрадь. Два ученика работают на индивидуальных досках для дальнейшей проверки работы.
У. Запишите число, которое больше 36 и меньше 38. Дети открывают ответы на досках. – Какое из этих чисел лишнее? Почему?
Д. 7 – однозначное. У. На какие группы можно разбить эти числа?
Д. На однозначные и двузначные. IV. Практическая работаУ. Возьмите каждый фигуру, которая лежит на подносе. Что это за фигура?
Д. Треугольник. У. Подумайте, как из него получить квадрат. Дети делят фигуру, как показано на рисунке, затем соединяют детали. Учитель повторяет правила безопасности при работе с ножницами. – Вы получили квадрат. Расскажите о нем. Д. У квадрата четыре вершины, четыре стороны, четыре угла. У. Что можно сказать об углах? Д. Они прямые. При помощи угольников или модели прямого угла выясняется, что углы у квадрата прямые. У. Возьмите в руки линейки, измерьте стороны квадрата. Д. Все стороны равны. У. Сколько углов и сторон у квадрата? Д. По четыре. У. Четное количество углов, сторон. Как можно назвать квадрат по-другому? Д. Четырехугольник. Учитель на доске фиксирует свойства квадрата. У. Рассмотрите рисунки на доске. На доске:
– Из каких геометрических фигур составлен первый рисунок? Д. Квадрат, два треугольника, круг. У. Какая фигура лишняя? Д. Круг, так как он не имеет углов. У. Из каких геометрических фигур составлен второй рисунок? Д. Прямоугольник, три треугольника, круг. У. Чем отличаются рисунки?
Д. Количеством треугольников и тем, что на первом рисунке – квадрат, а на втором – прямоугольник. У. О какой еще фигуре мы будем говорить? Д. О прямоугольнике. V. ФизкультминуткаVI. Знакомство с новым материаломУ. Я расскажу вам сказку. Она необычная, математическая и называется "Родственники". Жила на свете важная фигура. Важность ее признавалась всеми людьми, так как при изготовлении многих вещей форма ее служила образцом. Кого бы ни встретила она на своем пути, всем хвалилась: "Посмотрите, какой у меня красивый вид: стороны мои все равны, углы все прямые. Красивее меня нет фигуры на свете!" Учитель показывает рисунок. – Назовите эту фигуру, ребята! Д. Квадрат. У. Как вы узнали? Д. Стороны равны, углы прямые.
У. Ходил Квадрат по свету, и стало тяготить его одиночество: не с кем побеседовать и потрудиться в хорошей и дружной компании. Ведь весело и легко бывает только с друзьями. И решил Квадрат поискать родственников... "Если встречу родственника, то сразу его узнаю, – думал Квадрат, – ведь он должен быть похож на меня".
Пригляделся Квадрат к ней и увидел что-то знакомое. "Как тебя зовут?" – спрашивает. Д. Это прямоугольник. У. Почему он так называется? Д. У него все углы прямые. Осуществляется проверка у доски. У. Давайте измерим длину сторон. Что вы о них скажете? Д. Стороны, которые лежат одна против другой, равны. Учитель на доске фиксирует свойства прямоугольника. У. Называются эти стороны противоположными. Сформулируйте вывод о противоположных сторонах прямоугольника. Д. Противоположные стороны прямоугольника равны. У детей на партах по два прямоугольника разного цвета. Длина красного прямоугольника больше длины синего, а ширина одинакова. У. В этом можно также убедиться, не измеряя стороны по линейке. Предложите такой способ. Д. Наложением. У. Накладываем одну фигуру на другую и замечаем, что противоположные стороны равны. В чем же отличие квадрата от прямоугольника? Д. У квадрата все стороны равны, а у прямоугольника – только противоположные.
У. У прямоугольника та сторона, которая длиннее, называется "длина". Сторона, которая короче, называется "ширина". Д. У квадрата все стороны одинаковой длины. VII. Закрепление нового материалаУ. Давайте поучимся чертить прямоугольник, используя свойства сторон. Начертите прямоугольник, длина которого – 5 сантиметров, а ширина – 3 сантиметра. Как можно их расположить? На доске:
– Подумайте, можно ли из этого прямоугольника получить квадрат? Д. Взять за сторону квадрата ширину или длину прямоугольника. У. Начертите в тетради квадрат любым способом. Дети выполняют задание.
– Кто начертил квадрат со стороной 3 сантиметра, кто – со стороной 5 сантиметров? Д. У фигур четыре угла, все фигуры прямые, у них по четыре стороны, противоположные стороны равны. У. А какая же у них общая фамилия? Д. Прямоугольники. У. Обрадовались фигуры, что нашли друг друга. Отдыхают вместе, трудятся. Один раз гуляли на полянке, и прямо к ним направляется фигура, имеющая такой вид:
Вежливо поздоровавшись, говорит: "Долго я искал представителей нашего старинного рода. Наконец-то я нашел своих близких родственников!" Д. Четыре угла, четыре стороны. У. Так встретились и жили одной дружной семьей три родственные фигуры, которые назывались четырехугольники. К концу урока на доске появляется таблица:
VIII. Итог урокаУ. Какие утверждения правильны?
На доске:
Д. Правильные – первое и третье утверждение.
|
||||||||||
Тема. "Прямая линия, линии в тетради, точка пересечения линий, линованные и нелинованные листы".
Цель. Познакомить учащихся с линией и ее свойствами, графической грамотностью; упражнять в вычерчивании линий, резании по прямой; развивать внимание, глазомер, конструкторское мышление; воспитывать аккуратность, интерес к знаниям, трудолюбие.
Оборудование. Магнитофонная запись песенки Карлсона из мультфильма, игрушка или рисунок с изображением Карлсона, конверт с геометрическими фигурами: треугольник, круг, прямоугольник, квадрат.
ХОД УРОКА
I. Организационный момент
II. Повторение изученного
Звучит отрывок из песенки Карлсона из мультфильма "Малыш и Карлсон".
Учитель. Кто поет эту песенку?
Дети. Карлсон.
У. А вот и сам Карлсон прилетел.
У доски появляется игрушка или рисунок с изображением Карлсона.
– Что он нам принес?
Д. Конверт.
У. А в конверте геометрические фигуры. Назовите их.
Д. Треугольник, круг.
– Прямоугольник, квадрат.
![]()
У. Чем похожи геометрические фигуры?
Д. Цветом.
У. Чем они отличаются друг от друга?
Д. Формой и размером.
У. Сравните треугольник и квадрат.
Д. Они оба зеленого цвета. Но у треугольника – 3 стороны, а у квадрата – 4.
У. В конверте у Карлсона лежит еще одна карточка, а на ней... что это?
Д. Точка.

III. Знакомство детей с понятием "линия"
У. Послушайте сказку про точку.
Жила была маленькая точка. Это была очень красивая красная точка. (Учитель ставит на доске мелом точку, а дети – на листе фломастером.) Однажды точка подумала: "Как мне хочется иметь много друзей! Отправлюсь-ка я путешествовать и поищу подружек". Только вышла красная точка за ворота, а навстречу ей тоже точка идет, только зеленая. Спрашивает зеленая точка у красной, куда та идет.
– Иду искать друзей. Пойдем со мной рядом!
Через некоторое время встречают они синюю точку... Идут по дороге друзья-точки, и их становится все больше и больше. Становятся они рядом друг с другом, и получается... линия!
![]()
IV. Вычерчивание линий и знакомство с их свойствами
У. Начертите прямую линию по линейке. Имеет ли она начало и конец?
Д. Нет.
У. Из чего состоит прямая?
Д. Из точек.
У. На линии можно отметить любую точку.
На доске:
![]()
– Начертите линию от руки.
На доске:
Д. Это кривая линия. Имеет ли она начало и конец?
Д. Нет.
У. А это какая линия?
На доске:
Д. Замкнутая кривая линия.
V. Сравнение разлиновки в тетрадях
У. Сравните разлиновку в линейку и в клетку.
Дети рассматривают листы.
– Найдите линии пересекающиеся и непересекающиеся, точки пересечения линий.
Дети находят на своих листах и показывают на образце учителя.
Д. В тетради листы линованные.
На доске (крупно):
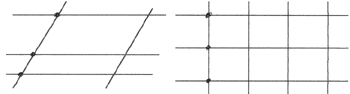
VI. Физкультминутка
На одной ноге постой-ка,
Если ты солдатик стойкий.
А теперь постой на левой,
Если ты солдатик смелый.
VII. Изготовление аппликации "Лодка с парусами"
У. Кто из мальчиков мечтает стать защитником Родины?
Мальчики поднимают руки.
– Какие рода войск вы знаете?
Д. Пехота, морской флот, авиация, артиллерия...
У. Подробнее остановимся на морском флоте. Какие военные плавающие средства вы знаете?
Д. Крейсер, подводная лодка, эсминец, катер...
У. Молодцы! А на чем можно выйти в море просто поплавать?
Д. На яхте, катере, лодке...
У. Вот сейчас мы будем изготавливать лодку с парусом. У вас на столах лежит цветная нелинованная бумага. Почему она так называется?
Д. На ней нет линий, как в тетрадях.
У детей лежат квадраты разных цветов.
У. Какая это фигура?
Д. Квадрат.
У. Как вы узнали?
Д. У него равны все 4 стороны.
У. Проведите внутри квадрата прямые линии с двух сторон линейки. Линейку положите так, чтобы одной стороной она проходила через правый верхний и левый нижний углы.
Учитель показывает выполнение действий на своем образце у доски.
На доске:
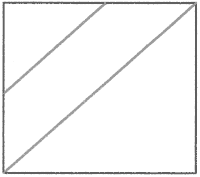
– Сплошные линии, которые вы провели, на чертеже обозначают линии разреза. Разрежьте ваши квадраты по линиям. Какие фигуры получились?
Д. Два треугольника и четырехугольник.
У. Чем отличаются треугольники?
Д. Размером.
У. А что у них общего?
Д. По две одинаковых стороны.
У. Из треугольников мы сделаем паруса, а четырехугольник будет основанием лодки.

VIII. Самостоятельная работа учащихся
Дети изготовляют аппликацию.
Учитель выставляет детские работы. Разбираются ошибки, допущенные в ходе самостоятельной работы. Выделяются лучшие лодочки.
IХ. Итог урока
У. Какие линии вы использовали?
Д. Прямые.
У. Что вы узнали о линии?
Д. У прямой линии нет начала и конца. Линия состоит из точек. Место пересечения линий называется точкой.
У. Молодцы! Вы хорошо трудились, а теперь убирайте ваши рабочие места.
Х. Домашнее задание
|
Тема. Построение вписанных многоугольников.
Цели. Ввести понятия вписанного многоугольника и описанной окружности; закреплять знания правил порядка действий в выражениях со скобками; отрабатывать умение решать уравнения и задачи с помощью уравнений. Оборудование. Учебник «Математика», печатная тетрадь; циркули; сигнальные светофоры.
ХОД УРОКА I. Организационный моментII. Постановка целей и задач урокаУчитель.
Есть о математике молва, Вот и мы сегодня продолжим развивать волю, смекалку и накапливать знания, отрабатывать умения. Вот какой план урока я вам предлагаю. На доске:
На обороте каждой карточки написано слово «Справились!».
III. Устный счетУ. Потренируем навыки устного счета. Дети открывают учебники и работают с примерами из задания.
– Читайте примеры, называя числа по-разному, в зависимости от действия. Найдите похожие примеры. Объясните, в чем они, на ваш взгляд, сходны, укажите различия. Задачу решите, используя чертеж. Дети выполняют задание. – Молодцы! У вас получилось. Учитель переворачивает первую карточку плана урока.
На доске:
IV. Знакомство с новым материалом
У. Сегодня мы с вами будем решать задачи из очень интересного раздела математики – геометрии. Учитель открывает запись на доске. На доске:
– Рассмотрите рисунок. На каком чертеже все вершины пятиугольника лежат на окружности? Волк или Заяц ответил правильно?
У. А какой рисунок получился у вас в домашней работе? Дети отвечают и показывают. У. Лежат ли вершины фигуры на окружности, которую вы начертили в домашнем задании? Д. Да. У. Как вы этого добились? Расскажите о своих действиях. Д. Центр окружности находится на пересечении диагоналей, а радиус равен половине диагонали. У. Какую ошибку совершил Волк? Что он не заметил? Д. Он не заметил, что окружность не проходит через одну вершину. У. Давайте прочитаем правило из учебника: если все вершины многоугольника лежат на окружности, то такой многоугольник называют вписанным в эту окружность. Мы завершили этот этап урока. Перевернем табличку. На доске:
У. Мы еще закрепим новую тему после физкультминутки. V. Физкультминутка
Большой пальчик мы потрем, VI. Практическая работаУ. Давайте посмотрим задание: как вписать в данную окружность:
1) треугольник; Эту работу выполним у доски. Учитель вывешивает табличку.
К доске выходит ученик. – Начертите окружность радиусом 3 сантиметра. Сколько нужно точек, чтобы начертить треугольник? Д. Три точки. У. Отметьте три любые точки на окружности красным карандашом и соедините их по линейке. К доске выходит следующий ученик.
Д. Четыре. У. Отметьте четыре точки на окружности синим карандашом и соедините их. Аналогично строится шестиугольник зеленым карандашом. – Какие фигуры-многоугольники у нас получились относительно окружности? Д. Вписанные в окружность. У. Эти фигуры равносторонние? Д. Нет. У. А вот Зайцу предстоит решить другую проблему. Прочитайте текст задачи. Дети читают текст задачи. «Заяц в своем саду решил разбить клумбу шестиугольной формы (все стороны этой клумбы равны). Каким способом это сделать?» У. Как ему помочь? Д. Надо сначала начертить окружность, а потом отметить на ней шесть точек, только на равном расстоянии. У. Давайте вспомним, как это сделать. Откройте «Рабочую тетрадь» и прочитайте задание. В этом задании нужно правильный шестиугольник вписать в окружность. Один ученик выполняет задание на доске – чертит окружность и отмечает на ней шесть точек с помощью циркуля с раствором, равным радиусу окружности. – Работайте красным карандашом при построении шестиугольника. А если понадобится начертить равносторонний треугольник? Д. Из шести точек, отмеченных для шестиугольника, выберем три, через одну от начальной, и соединим их. У. Треугольник начертите синим карандашом. Дети выполняют задание. – Молодцы! Вот мы и одолели новую тему. На доске переворачивается табличка. На доске:
VII. ФизкультминуткаVIII. Решение задачУ. Прочитайте название следующего этапа урока. Д. Решение задач. У. Для решения задач мы будем использовать уравнения. Дети читают текст задачи. «Через 5 лет Вове будет 17 лет. Сколько лет Вове сейчас?» Один ученик у доски решает задачу с комментированием. Пусть сейчас Вове х лет. Составим уравнение. На доске:
На доске переворачивается табличка. На доске:
IХ. Итог урокаУ. Посмотрите на наши таблички. На доске:
– Как стало светло и радостно от этих ярких цветов, а главное – от того, что мы выполнили все, запланированное нами! Чему мы учились? Д. Строить вписанные многоугольники. У. Оцените свою работу. Х. Упражнения на релаксациюУчитель просит детей принять позу покоя: сесть на стуле ближе к краю сиденья, спину держать прямо, руки положить свободно на коленях, глаза можно закрыть.
У. Все умеют танцевать, ХI. Домашнее задание
|
|
Тема. "Закрепление знаний о геометрических фигурах".
Цели. Закрепить знания о геометрических фигурах; умение решать примеры в столбик на сложение и вычитание двузначных чисел; развивать наблюдательность, познавательные способности, мышление, пространственное воображение, навыки узнавания геометрических фигур; умение использовать математические термины; воспитывать правильное научное мировоззрение; расширять представление об окружающем мире.
Оборудование. Учебник "Математика"; карта-схема "Полет в космос"; методическое пособие "книжка"; линейки; цветные мелки; веревочки; перфокарты; наборы геометрических фигур; магнитофон; запись музыки "Взлет", "Приземление"; мелодия песни "Чему учат в школе"; цветные карандаши.
ХОД УРОКА
I. Организационный моментII. Сообщение темы урокаУчитель. Сегодня на уроке математики мы закрепим ваши знания о геометрических фигурах и умение решать примеры в столбик на сложение и вычитание двузначных чисел. Но урок у нас необычный. Мы совершим полет в космос. Во время полета будьте дружны, поступайте по-товарищески, не забывайте, что мы единый коллектив.
III. Подготовительная беседаНа доске открывается карта-схема полета.
У. Начинаем подготовку к полету. Как звали первого космонавта нашей страны?
Дети. Юрий Алексеевич Гагарин. У. Как назывался космический корабль, на котором Юрий Алексеевич Гагарин поднялся в космос? Д. "Восток". У. Какие современные космические корабли вы знаете? Д. "Шатл", "Колумбия", "Союз". IV. Устный счетНа партах у учеников наборы с геометрическими фигурами. У. Открываем конструкторское бюро. Работаем в парах. Из набора геометрических фигур строим космическую ракету. Дети выполняют задание.
– Из каких геометрических фигур состоит наша ракета? Д. Из треугольников и квадрата. У. Сколько треугольников? Д. Три. У. Почему вы решили, что это треугольники? Д. Фигуры имеют три угла, три вершины, три стороны. У. Посмотрите на центральную часть ракеты. Какая это фигура? Д. Прямоугольник. У. Что вы знаете о прямоугольнике? Д. Он имеет четыре стороны, четыре вершины, четыре прямых угла. У. Что вы еще знаете об этой фигуре? Д. Противоположные стороны прямоугольника равны. У. Измерьте длину сторон прямоугольника. Чему они равны? Д. 10 см и 5 см. У. Найдите периметр прямоугольника. Давайте вспомним, что называется периметром. Д. Периметр – это сумма длин всех сторон. У. Чему же равен периметр? Д. 30 см. У. Как вы находили периметр? Дети отвечают. – Молодцы! Чтобы наша ракета взлетела, нужно узнать зашифрованное слово. Для этого выполните вычисления и воспользуйтесь буквенным ключом. Считайте устно, а ответы записывайте в тетрадь. На магнитной доске первый лист методического пособия "книжка". Дети выполняют задание. – Запишите ответы на второй строчке в порядке возрастания, а под ними – буквы. Д.
У. Какое слово получилось? Д. Взлет. У. Начинаем отсчет дружно, все вместе. Д. 5, 4, 3, 2, 1 – пуск! Звучит музыка "Взлет", на карте-схеме проводится линия к Луне.
V. Закрепление пройденного материалаУ. Мы с вами совершили посадку на Луну. Но первые люди спустились на поверхность Луны еще в 1969 году. Это были американские астронавты Нейл Армстронг и Эдвин Олдрин. Здесь нам предстоит выполнить математическое задание – решить примеры предложенные учителем.
Работаем по вариантам.
Дети выполняют задание в тетрадях. Вариант 1
Вариант 2
Проводится проверка примеров. – Как записывают примеры в столбик на сложение и вычитание двузначных чисел? Д. Единицы пишут под единицами, десятки пишут под десятками. У. Как складывают двузначные числа? Д. Единицы с единицами, десятки с десятками. У. Как вычитают двузначные числа? Д. Единицы вычитают из единиц, десятки вычитают из десятков. У. Хорошо. Закройте учебник. Можно отправляться на другую планету. VI. ФизкультминуткаУчитель включает аудиокассету. Под музыку песни "Чему учат в школе" дети выполняют физические упражнения. VII. Закрепление пройденного материала (продолжение)У. Мы прилетели на планету Марс. На карте-схеме проводится линия.
– Вы хотели бы что-нибудь узнать об этой планете? По усмотрению учителя можно подобрать материал для небольшого сообщения о Марсе. Вот какое задание вам предлагается на Марсе: Найдите знакомые вам геометрические фигуры. Вспомните, как они называются.
На магнитной доске открывается второй лист методического пособия "книжка".
Дети отвечают. – А теперь давайте сделаем некоторые построения. На классной доске построение выполняет учитель, дети работают в тетрадях, выполняя все этапы задания.
– Начертите прямую линию. Можем ли мы изобразить всю прямую?
Д. Нет. У. Почему? Д. Она продлевается в обе стороны бесконечно. У. Что же мы чертим? Д. Часть прямой. У. Отметьте на ней точку А. Как получить отрезок? Д. Надо поставить еще точку. У. Обозначим ее буквой С. Назовите отрезок.
Д. Отрезок АС. У. Что такое отрезок? Д. Часть прямой, ограниченная двумя точками. У. Отметьте красным карандашом отрезок АС. Как называются незакрашенные части прямой? Д. Лучи. У. Верно. Покажите их. Что такое луч? Д. Часть прямой, у которой есть начало, но нет конца. Учитель раздает детям веревочки.
У. А сейчас попробуем получить эти фигуры практически – на веревочке. Ваши пальчики – это точки. Дети выполняют задание. – Молодцы! Летим дальше. Наш путь лежит на планету Юпитер. Пока ракета идет на автопилоте, вам предстоит выполнить еще одно интересное задание. На столе у вас перфокарты. Надо самостоятельно найти периметр фигуры, данной в ней. Детям предложено четыре варианта карточек. Они выполняют задание, записывая решение в тетрадях. – Мы прибыли на планету Юпитер (на карте-схеме проводится линия). Это самая большая планета Солнечной системы. Посмотрите на карту-схему. Какая геометрическая фигура изображает наш маршрут? Д. Ломаная. У. Сколько в ней звеньев? Д. Три. У. Постройте самостоятельно ломаную из трех звеньев с длинами 7 см, 3 см, 2 см. Работаем цветными карандашами. Найдите длину ломаной, начертите отрезок такой же длины. Дети выполняют задание. – Много интересных математических заданий выполнили мы, путешествуя по планетам Солнечной системы. Пора возвращаться на Землю, где нас любят и ждут. Чтобы вернуться, надо дружно всем вместе отгадать кроссворд. VIII. Итог урокаНа магнитной доске – третий лист методического пособия "книжка".
1. Мера длины, состоящая из 10 дм. Ответы: 1. Метр. 2. Ромб. 3. Луч. 4. Точка. 5. Квадрат. 6. Цифра. 7. Четыре. У. Какое слово получилось в выделенных клетках? Д. Молодцы.
На карте-схеме проводится линия к Земле.
У. Из полета возвратились На магнитной доске – четвертый лист методического пособия "книжка".
Выслушиваются ответы детей. – Спасибо за работу! Урок окончен. IХ. Домашнее задание
|
|
Тема. «Величины и их преобразование. Решение задач».
Цели. Закреплять знания о величинах и единицах их измерения; формировать умение решать задачи на нахождение площади квадрата и прямоугольника, расстояния по данным скорости и времени; развивать память, воображение, мышление. Оборудование. Карта мира; наборы геометрических фигур для работы у доски и в парах; видеодвойка; аудиомагнитофон; рисунки животных Африки; карточки.
ХОД УРОКА I. Организационный моментII. Сообщение темы урокаУчитель прикрепляет на доску иллюстрации с изображениями животных. Учитель. Каких животных вы видите на рисунках? Дети. Здесь изображены слон, обезьяна, зебра, крокодил, носорог. У. Где они живут? Д. В Африке. У. Правильно. На сегодняшнем уроке я предлагаю вам совершить воображаемое путешествие в то место мира, где не бывает зимы, – в Африку. Покажите ее на карте. Учащийся, вызванный к доске, выполняет задание. – В пути вам предстоит выполнять различные математические задания, решать задачи. Для этого вам понадобятся знания по теме «Величины». Готовы ли вы к путешествию? Д. Да. III. Работа с геометрическим материалом
У. У меня есть описание маршрута путешествия. Предлагаю вам начертить в тетрадях схему этого маршрута. Возьмем масштаб, который указан на нашей карте, – 1:25 000 000. Д. В 1 см, отмеренном на бумаге, вмещается 25000000 см на поверхности земли. У. Ответ правильный. Сколько километров в 25 000 000 см? Д. 250 км. У. Схема займет полстраницы. Итак, начало маршрута – Харьков. Поставьте точку приблизительно в середине строки. Первая остановка будет в направлении вниз на 40 мм. Вторая остановка – вниз на 70 мм и влево на 40 мм. Третья остановка – Африка – находится на 5 мм вниз и на 40 мм влево. Какая геометрическая фигура получилась? Д. Ломаная. У. Возвращаться мы будем самым коротким путем. Дети соединяют линией точку, обозначающую Африку, с точкой, обозначающей Харьков. – Как называется эта линия? Д. Прямая. У. Используя масштаб, посчитайте расстояние от Харькова до Африки по ломаной линии, а затем по прямой. Сравните, на сколько километров меньше расстояние по прямой. Учащиеся считают длину ломаной и умножают 250 на это число. Потом измеряют длину прямой и умножают 250 на это число, затем находят разность. – Найдите общее расстояние нашего маршрута. Дети находят сумму. – Выберем подходящий вид транспорта, чтобы путешествие было неутомительным. Для этого используем подсказки учебника, где даны средние скорости разных видов транспорта. После тщательного анализа учащиеся выбирают самолет. – Построим самолет из геометрических фигур. Кто самый смелый? Один ученик, вышедший по желанию, строит самолет на магнитной доске. Называет каждую геометрическую фигуру. Остальные дети работают парами, используя геометрический материал, предложенный учителем. Работа проверяется. На доске:
У. Самолет готов. Полетели! Д. Ура! Полетели! IV. Проверка домашнего заданияУ. Пока летим, проверим домашнее задание, то есть то, что вы узнали об Африке и какие математические задания подготовили ребятам класса. В тетрадях записываем только выражения и находим их значения. На закрытых частях доски работают два ученика. По их ответам проводится проверка выполнения задания классом. Дети с мест читают составленные дома задачи, класс решает их и записывает решения в тетрадях. Ученик 1. Самая большая река Африки – Нил. Его длина 6671 км. Сколько это метров? (6 671 000 м.) Протяженность реки Нигер 4160 км. На сколько километров река Нил длиннее реки Нигер? (2511 км.) Ученик 2. В Африке растет бамбук. Это трава, хотя и очень прочная. Удочки, лыжные палки – это изделия из бамбука. А в Африке из бамбука делают хижины. Скорость роста этого растения очень высока. За одни сутки бамбук вырастает на 50 см. Какой высоты достигнет бамбук за неделю? (350 см.)
Ученик 3. Во многих африканских домах есть верный друг и помощник – слон. Это самое огромное животное суши. Его масса достигает 6 т. Сколько это центнеров? (60 ц.) А килограммов? (6 000 кг.)
Ученик 4. Бивни крупного слона вырастают до трех с половиной метров. Сколько это сантиметров? (350 см).
Учитель. Какую площадь займут уши 10 слонов? (20 м2). Ученик 5. За день жираф съедает 80 кг зеленой массы, а слон в 4 раза больше. Какая масса зелени потребуется жирафу и слону вместе на 5 дней? (80 х 4 + 80) х 5 = 2 000 (кг).) Ученик 6. Самая большая лягушка в мире – это лягушка-голиаф, живущая в западной Африке. Ее масса достигает 3 кг. Горилла – самая крупная из обезьян. Она обитает в африканских тропических лесах. Масса гориллы в 87 раз больше массы лягушки-голиаф. Каков вес гориллы? (87 х 3 = 261 (кг)).
Ученик 7. Верблюд может нести половину собственного веса – 350 кг, а самец ламы может У. Подведем итоги. Назовите все величины, которые встретились при решении задач. Дети называют, а учитель вывешивает на доску названия величин: длина, скорость, время, масса, площадь. – Поменяйтесь, пожалуйста, тетрадями, проверьте и оцените работу друг друга. Для проверки открывается доска с правильными ответами. У. Летим дальше. V. Самостоятельная работа учащихсяУ. Стоп! Пора остановиться. Учитель раздает детям карточки для самостоятельной работы. После выполнения задания дети сдают карточки на проверку. 1. Заполни пропуски и получи верные равенства:
а) 86 709 кг = ц ... кг = ... т ... ц ... кг = ... т ... кг 2. Установи закономерность и продолжи каждый ряд величин:
а) 8 км 30 м, 24 км 90 м, 72 км 270 м, ... км ... м VI. Решение задачУ. Приготовим Лего и отправимся дальше. Решим такую задачу. От Харькова до первой посадки наш самолет летел 4 часа со скоростью 400 км/ч. От первой посадки до второй он летел столько же времени, увеличив скорость в 2 раза. Во сколько раз большее расстояние он пролетел? Условие задачи сконструируйте из Лего. Условие:
Вывод: если скорость увеличить в 2 раза, то расстояние увеличится во столько же раз. Зависимость между скоростью и расстоянием можно записать формулой S = V х t. Из этой формулы видно, что расстояние находится в такой же зависимости и от времени, и от скорости, так как и скорость, и время – множители, а расстояние – значение произведения. Составим план решения задачи. Дети работают самостоятельно. Учитель помогает слабым ученикам. Решение:
1) 400 х 4 = 1600 (км)
Ответ: в 2 раза больше. VII. ФизкультминуткаУ. Наш самолет приземляется в Африке. Вы рады? Д. Да! У. Тогда потанцуем под музыку. Звучит песня из кинофильма «Красная Шапочка»:
В Африке горы вот такой вышины, У. Много интересного можно увидеть в Африке. Это и самая жаркая пустыня Сахара, и одно из чудес света – египетские пирамиды, джунгли с их необычной растительностью и животным миром и многое-многое другое. Однако нам пора возвращаться в школу. Садимся в самолет. На обратном пути нас ждет интересное математическое задание. VIII. Решение задач (продолжение)Для выполнения задания предлагается фигура, которую можно разбить на квадраты и прямоугольники, а также достроить до квадрата или прямоугольника. У. Приготовьтесь работать с Лего в парах. Представьте себе площадь Африки вместе с прилегающими островами в виде прямоугольника с длиной стороны 6 единиц (1 единица – площадь поверхности одного кубика) и шириной 5 единиц, причем площадь островов составляет 4 единицы. Обозначим ее для удобства в виде квадрата другого цвета. Вычислите площадь Африки без островов. Найдите все возможные способы решения. Дети конструируют условие задачи из конструктора Лего. Решение
У. Вычислите площадь Африки вместе с островами, если 1 единица соответствует 1 млн. км2. Решение: 1 000 000 х 30 = 30 000 000 (км2) Такова примерная площадь материка. IX. Итог урокаУ. Внимание! Наш самолет совершил посадку в Москве. Понравилось ли вам путешествие, ребята? С какими величинами вы работали? В каких единицах измеряется площадь? По какой формуле вычисляется площадь прямоугольника? В каких единицах измеряется скорость? А по какой находится расстояние? Что общего между этими двумя зависимостями? Дети отвечают на вопросы. – Молодцы! Летали мы сегодня с пользой. Х. Домашнее заданиеУчитель раздает детям карточки с заданиями. Решить задачу. Составить и решить две обратные задачи. Найти расстояние от Москвы до Африки, если самолет будет лететь 4 часа без остановок со средней скоростью 875 км/ч. |
СПИСОК ЛИТЕРАТУРЫ
- Кавун И.Н. Начальный курс геометрии. Изд-во «Поиск». Москва, 2003.
- Звонкин А.В. Малыши и математика. Изд-во Московский центр непрерывного математического образования. 2006.
- Житомирский В.Г. Геометрия для малышей. Изд-во «Педагогика». Москва, 1995.
- Перелыгина Е.А. Методические рекомендации по формированию ключевых компетентностей учащихся начальной школы. Самара, 2007.
- Дубова М.В. Комплексный подход в начальном общем образовании: современное состояние и проблемы. Педагогическое образование и наука, 2008, № 8, с.84-86.
- Тихоненко А.В. К вопросам о формировании ключевых компетентностей младших школьников. Начальная школа, 2008, № 4, с. 78-84.


про публікацію авторської розробки
Додати розробку