"Геометричні перетворення. Симетрія в природі"

Симетрія в природі

«... Бути прекрасним означає бути симетричним і пропорційним».

 Платон

Важко знайти людину, яка б не мала якогось уявлення про симетрію. "Симетрія" - слово грецького походження. Воно, як і слово "гармонія", означає відповідність, наявність певного порядку, закономірності в розташуванні 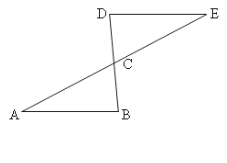частин.

В математиці розглядаються різні види симетрії:

• осьова симетрія (симетрія відносно прямої),
• центральна симетрія (симетрія відносно точки) і
• дзеркальна симетрія (симетрія відносно площини).

Відомості з курсу математики:

Центральна симетрія. Геометрична фігура називається симетричною відносно центру C, якщо для кожної точки А цієї фігури може бути знайдена точка E цієй ж фігури, так що відрізок AE проходить через центр C і ділиться в цій точці навпіл (AC = CE). Точка С називається центром симетрії. 

Природа - дивовижний творець і майстер. Все живе в природі має властивість симетрії.

Відомості з курсу математики: 

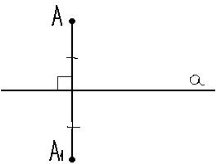
Осьова симетрія. Симетричними відносно прямої а називаються точки А і А1, якщо ця пряма проходить через середину відрізка АА1 і перпендикулярна до нього. Пряма а - це вісь симетрії.

Якщо зверху подивитися на будь-яку комаху і подумки провести посередині пряму (площину), то ліві і праві половинки комах будуть однаковими і по розташуванню, і за розмірами, і за забарвленням. Адже ми ні разу не бачили, щоб у жука або бабки, у будь-якої іншої комахи лапи ліворуч були б ближче до голови, ніж праворуч, а праве крило метелика або сонечка було б більше, ніж ліве. Такого в природі не буває, інакше б комахи не змогли б літати.

 Властивість симетричності, властиве живій природі, людина використала у своїх досягненнях, винайшовши літак, створивши унікальні будівлі архітектури. Та й сама людина є фігурою симетричною.

Симетрію можна побачити серед квітів. Осьову симетрію мають квітки сімейства розоцвітих, а центральну симетрію - сімейство хрестоцвітих. Симетрію можна побачити і на листі дерев. 

Відомості з курсу математики. Дзеркальна симетрія. Геометрична фігура називається симетричною відносно площини S, якщо для кожної точки E цієї фігури може бути знайдена точка E 'цієї ж фігури, так що відрізок EE' перпендикулярний площині S і ділиться цією площиною навпіл(EA = AE). Площина S називається площиною симетрії. Симетрині фігури, предмети і тіла не рівні один одному у вузькому сенсі слова (наприклад, ліва рукавичка не підходить для правої руки і навпаки). Вони називаються дзеркальнорівними.

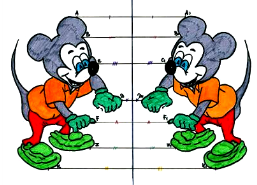
Симетрія, характерна для представників тваринного світу, називається білатеральною симетрією.

Проте симетрія існує і там, де її не видно на перший погляд. Фізик скаже, що всяке тверде тіло - кристал. Хімік скаже, що всі тіла складаються з молекул, а молекули складаються з атомів. А багато атомів розташовуються в просторі за принципом симетрії.

Таким чином, дане перетворення фігур (симетрія) увійшло в математику в результаті спостереження людини за навколишнім світом. Воно зустрічається часто і повсюдно. Тому навіть не досвідчена людина зазвичай легко вбачає симетрію у відносно простих її проявах.

Симетрія в кристаллах

В хмарах і в надрах Землі, на гірських вершинах і в піщаних пустелях, в океанах і морях, в наукових лабораторіях і в рослинних клітинах - скрізь зустрічаються кристали. Як на Землі, так і на інших планетах, на далеких зірках весь час безперервно виникають, зростають і руйнуються кристали. Метеорити також складаються з кристалів, при цьому іноді в їх склад входять кристалічні речовини, які не зустрічаються на Землі.

Кристали скрізь. Люди повсякденно використовують кристали, роблять з них прикраси, милуються ними.

Науковці вивчили властивості кристалів, навчились вирощувати штучні кристали. Область застосувань кристалів значно розширилась, вони стали займати суттєве місце в новітніх технологіях. Кристали одні з найгарніших і найзагадковіших творінь природи. 

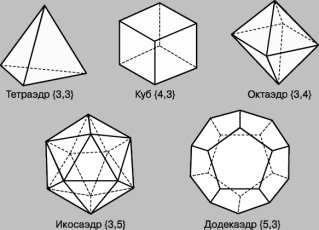
    Що ж таке кристал? Шкільний підручник дає таке означення: кристал- це тверде тіло, що утворюється в природних або лабораторних умовах і має вид багатогранника. Поверхня таких фігур обмежена досконалими площинами-гранями. Грані перетинаються по прямих лініях -ребрах. Точки перетину ребер утворюють вершини.

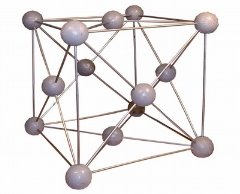    У природі існує багато кристалів і так само багато існує різних форм кристалів. Тому дуже важко дати означення, яке підходило б до всіх кристалів. Але, якщо скористатись можливостями науки, зокрема, рентгенівським аналізом кристалів, то можна побачити атоми всередині кристалічного тіла, визначити їх просторове розташування. В результаті застосування рентгенівських променів було встановлено, що рішуче всі кристали складаються з елементарних частинок, розташованих в строгому порядку. Отже, можна сказати, що кристалами називаються всі тверді тіла, що складаються з частинок (атомів, іонів, молекул), розташованих строго закономірно.

 Розглядаючи різні кристали, ми бачимо, що всі вони різні за формою, але будь-який з них є симетричним тілом. І дійсно симетричність - це одна з основних властивостей кристалів.

Всі кристали симетричні. Це означає, що в кожному кристалічному многограннику можна знайти площині симетрії, осі симетрії, центри симетрії та інші елементи симетрії такі, що відображають многогранник сам на себе. Найбільш відомі кристали: алмаз, кремній, алюміній, золото, графіт, срібло, цинк, гіпс, кварц та інші.