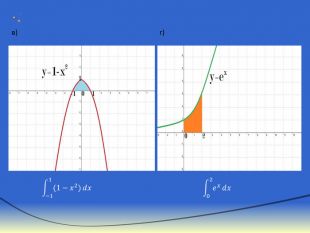
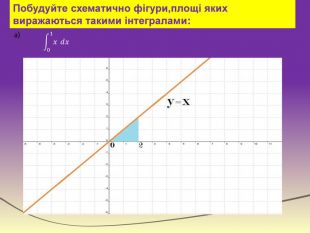
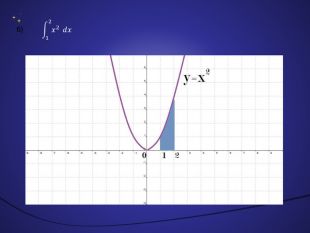
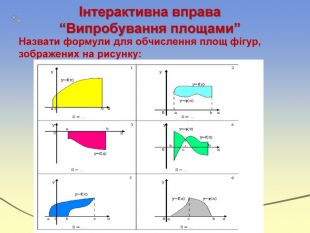
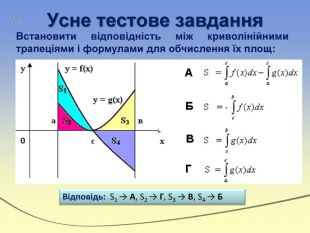
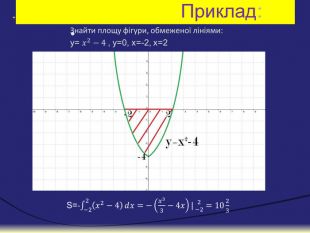
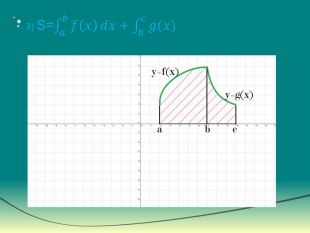
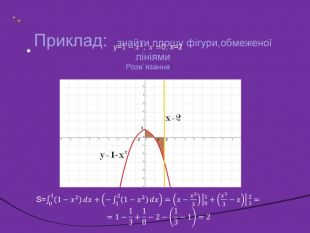
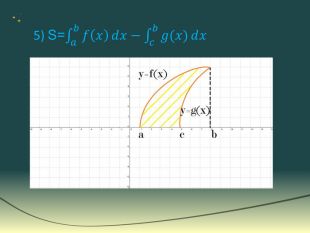
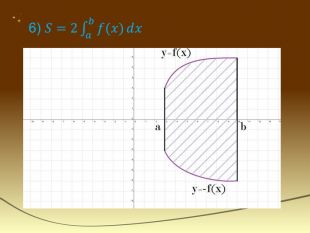
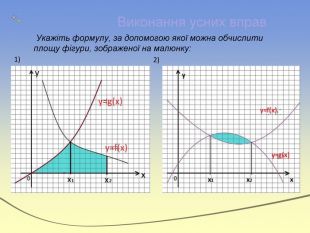
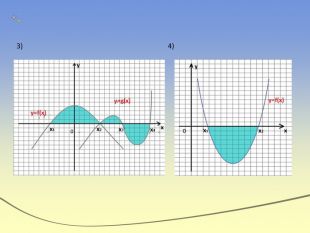
Інтеграл та його застосування








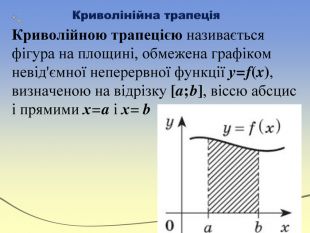
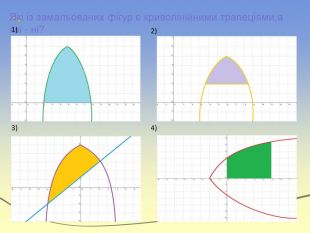
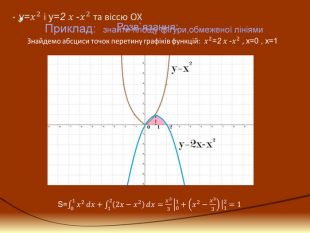
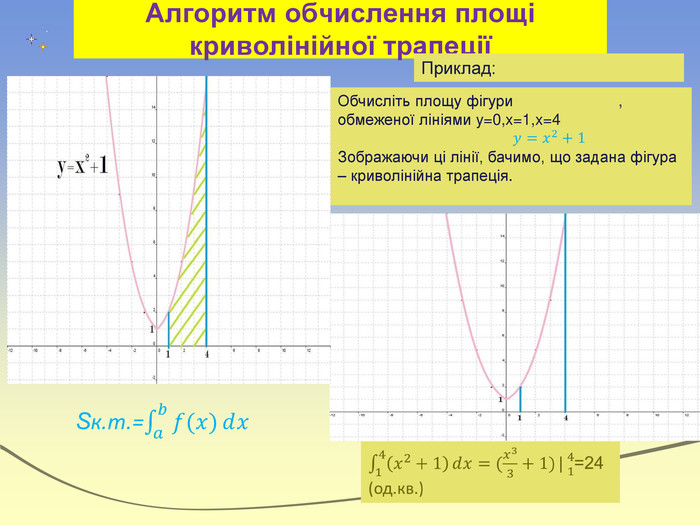
![Криволінійна трапеція. Криволійною трапецією називається фігура на площині, обмежена графіком невід'ємної неперервної функції у = f(x), визначеною на відрізку [a; b], віссю абсцис і прямими х = a і х = b Криволінійна трапеція. Криволійною трапецією називається фігура на площині, обмежена графіком невід'ємної неперервної функції у = f(x), визначеною на відрізку [a; b], віссю абсцис і прямими х = a і х = b](/uploads/files/36948/269125/293148_images/9.jpg)
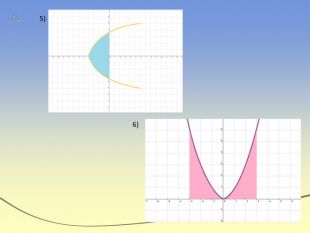
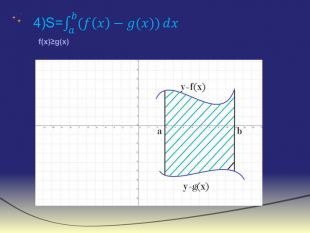
![Формула Ньютона-Лейбніца. Якщо f(x) визначена і неперервна на відрізку [a;b] , а F(x) її довільна первісна на цьому відрізку(F`(x)=f(x)) то :- формула Ньютона-Лейбніца Приклад: Формула Ньютона-Лейбніца. Якщо f(x) визначена і неперервна на відрізку [a;b] , а F(x) її довільна первісна на цьому відрізку(F`(x)=f(x)) то :- формула Ньютона-Лейбніца Приклад:](/uploads/files/36948/269125/293148_images/11.jpg)
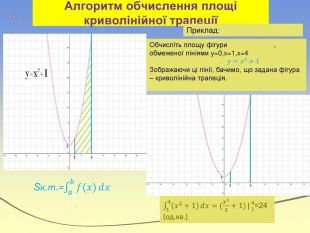
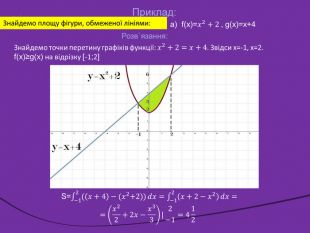
![Визначений інтеграл. Для кожної неперервної на відрізку [а;b] функції визначений iнтеграл існує. За формулою Ньютона-Лейбнiца потрібно: 1) знайти будь-яку первісну F функції f(х) на відрізку [а; b];2) обчислити значення первісної у точках х = b та х = а;3) знайти різницю F(b) - F(а).𝑎𝑏𝑓𝑥𝑑𝑥=𝐹𝑏−𝐹𝑎=𝐹(𝑥)𝑏𝑎 Властивості визначеного інтеграла Визначений інтеграл. Для кожної неперервної на відрізку [а;b] функції визначений iнтеграл існує. За формулою Ньютона-Лейбнiца потрібно: 1) знайти будь-яку первісну F функції f(х) на відрізку [а; b];2) обчислити значення первісної у точках х = b та х = а;3) знайти різницю F(b) - F(а).𝑎𝑏𝑓𝑥𝑑𝑥=𝐹𝑏−𝐹𝑎=𝐹(𝑥)𝑏𝑎 Властивості визначеного інтеграла](/uploads/files/36948/269125/293148_images/12.jpg)


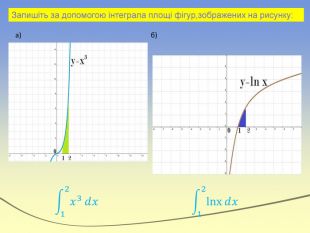
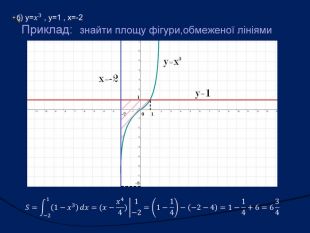
![Геометричний зміст. Геометричним змістом визначеного інтеграла є знаходження площі криволінійної трапеції. Нехай на відрізку [a;b] на осі ОХ задано функцію f(x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру обмежену графіком функції f(x) відрізком [a;b] осі ОХ, прямими х=а і х=в, називають криволінійною трапеціею. Геометричний зміст. Геометричним змістом визначеного інтеграла є знаходження площі криволінійної трапеції. Нехай на відрізку [a;b] на осі ОХ задано функцію f(x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру обмежену графіком функції f(x) відрізком [a;b] осі ОХ, прямими х=а і х=в, називають криволінійною трапеціею.](/uploads/files/36948/269125/293148_images/15.jpg)



![Інтерактивна вправа“Перевір себе”Вкажіть неправильну рівність стосовно властивостей визначених інтегралів., сє [a,b]1.2.3.4.5. Інтерактивна вправа“Перевір себе”Вкажіть неправильну рівність стосовно властивостей визначених інтегралів., сє [a,b]1.2.3.4.5.](/uploads/files/36948/269125/293148_images/27.jpg)


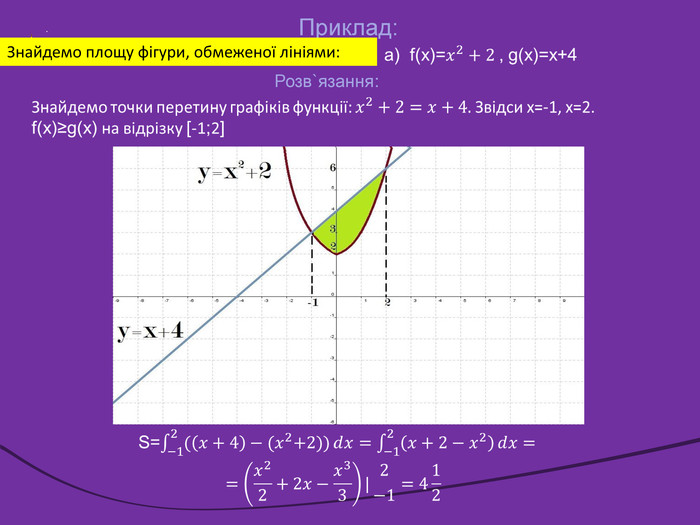
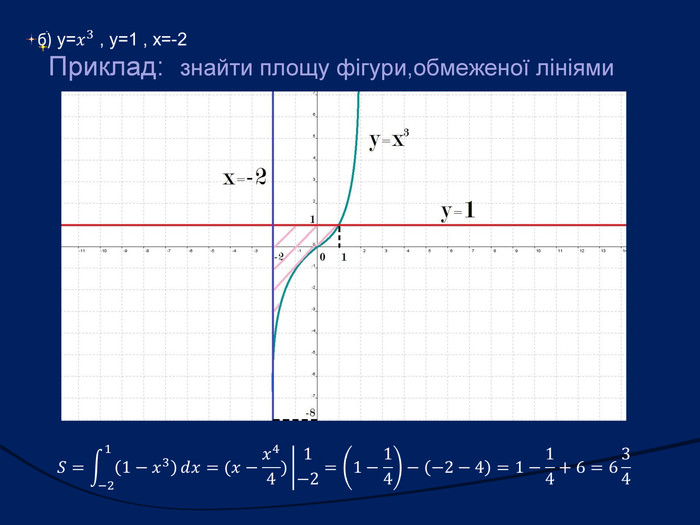
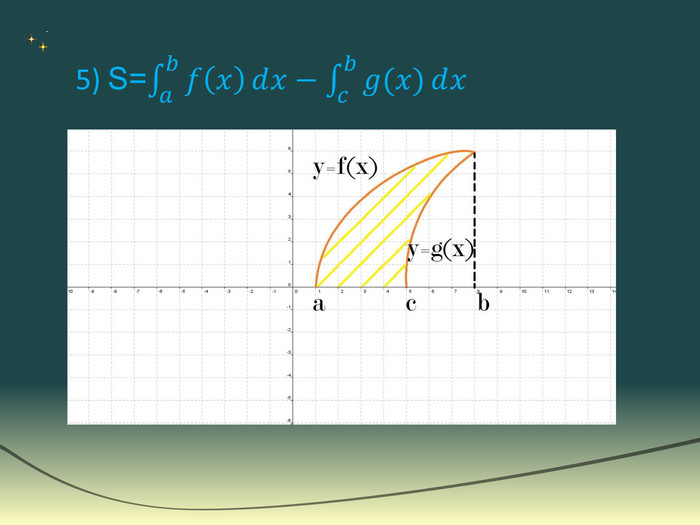
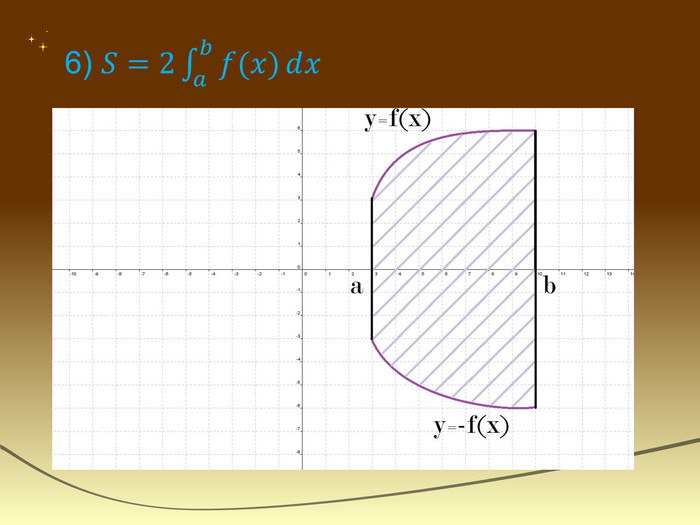






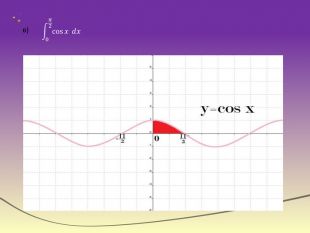
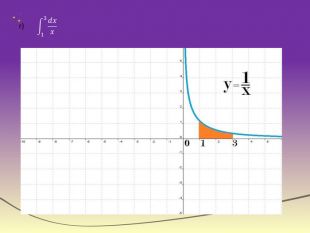
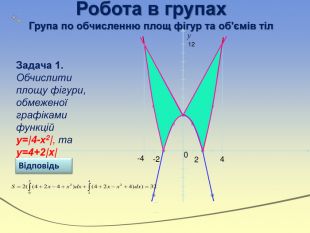
![Робота в групах. Група по розв'язуванню рівнянь та нерівностей1) Розв’язати нерівність: Відповідь: х є [-4;4] . 2) Розв’язати рівняння: Відповідь: ±π/3+πn, n є Z. Робота в групах. Група по розв'язуванню рівнянь та нерівностей1) Розв’язати нерівність: Відповідь: х є [-4;4] . 2) Розв’язати рівняння: Відповідь: ±π/3+πn, n є Z.](/uploads/files/36948/269125/293148_images/55.jpg)
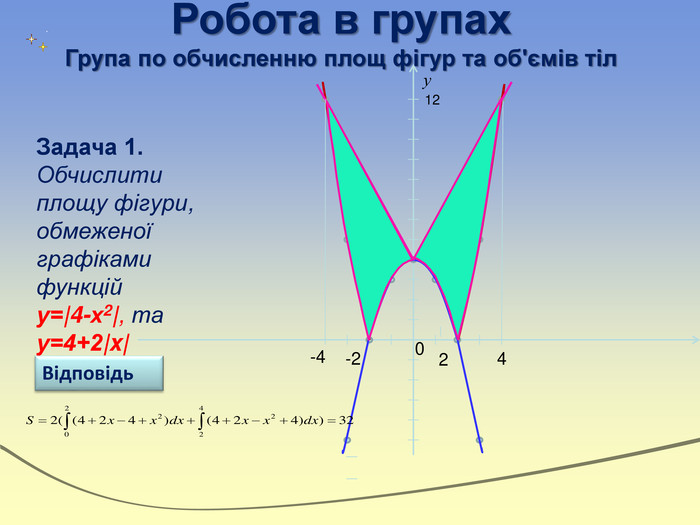
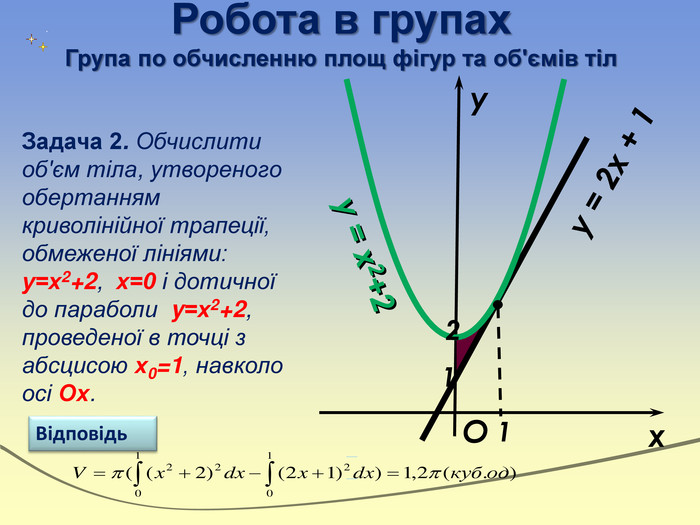









Дидактична: пояснити та систематизувати знання учнів про інтеграл, відпрацювати навички знаходження інтегралів , їх застосування до розв'язування задач, навчати учнів бачити єдину математичну модель у різних ситуаціях, складати її в нестандартних умовах. Розвиваюча: розвивати навики самостійного мислення, інтелектуальні навики (аналіз, синтез, порівняння, співставлення), увагу, пам’ять, спостережливість, формувати вміння виступати перед аудиторією. Виховна: виховувати вміння раціонально використовувати робочий час,математичну культуру учнів, підвищувати інтерес до предмету шляхом звернення до історичних джерел. Мета уроку
Історична довідка. Як відомо,Ньютон використовував у ролі інтеграла позначку квадрата(перед позначенням функції або навколо неї),але використовувати таке позначення було досить незручно. Сучасну позначку визначеного інтеграла ввів Лейбніц у 1675 році. Він утворив інтегральний символ ∫ з літери S – скорочення латинського слова summa. Сучасне поняття визначеного інтеграла з вказаними межами інтегрування були вперше запропоновані Жаном Батистом Фурье в 1819-20 роках.
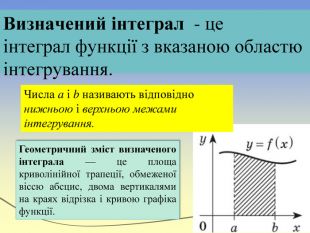
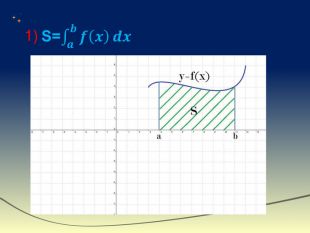
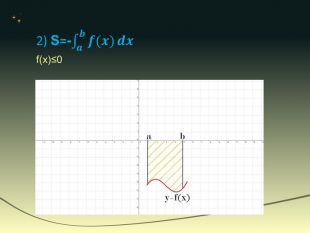
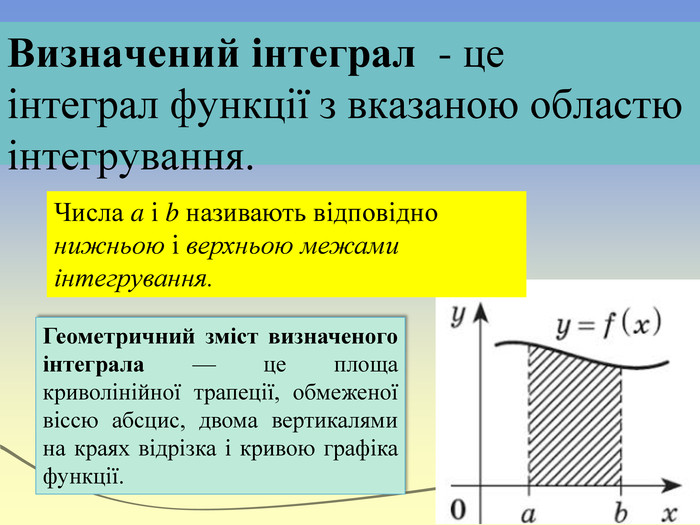
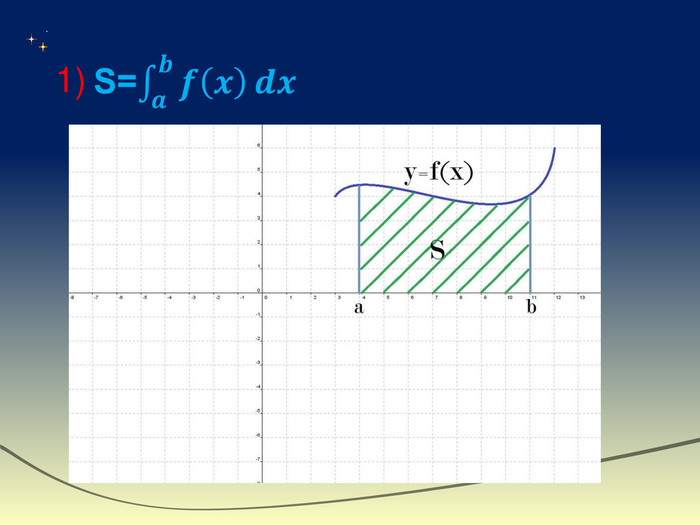
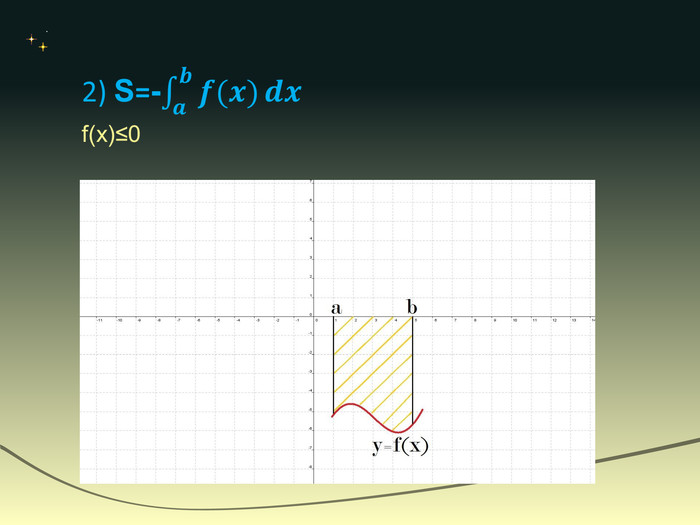
Визначений інтеграл - це інтеграл функції з вказаною областю інтегрування. Геометричний зміст визначеного інтеграла — це площа криволінійної трапеції, обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції. Числа a і b називають відповідно нижньою і верхньою межами інтегрування.
Визначений інтеграл. Для кожної неперервної на відрізку [а;b] функції визначений iнтеграл існує. За формулою Ньютона-Лейбнiца потрібно: 1) знайти будь-яку первісну F функції f(х) на відрізку [а; b];2) обчислити значення первісної у точках х = b та х = а;3) знайти різницю F(b) - F(а).𝑎𝑏𝑓𝑥𝑑𝑥=𝐹𝑏−𝐹𝑎=𝐹(𝑥)𝑏𝑎 Властивості визначеного інтеграла
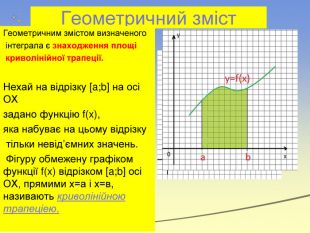
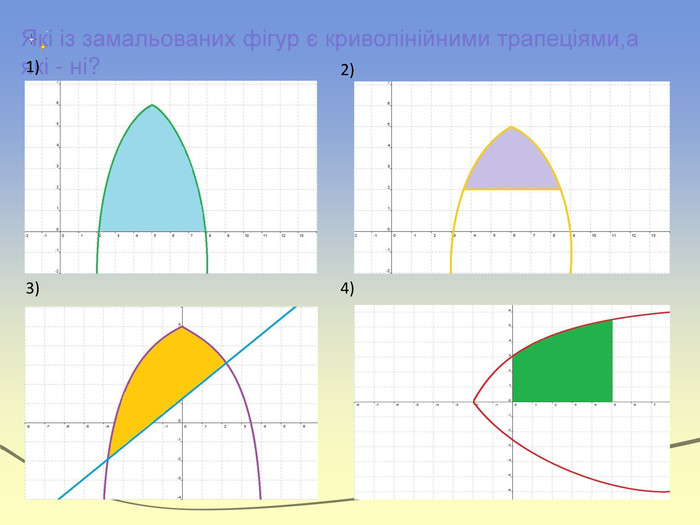
Геометричний зміст. Геометричним змістом визначеного інтеграла є знаходження площі криволінійної трапеції. Нехай на відрізку [a;b] на осі ОХ задано функцію f(x), яка набуває на цьому відрізку тільки невід’ємних значень. Фігуру обмежену графіком функції f(x) відрізком [a;b] осі ОХ, прямими х=а і х=в, називають криволінійною трапеціею.
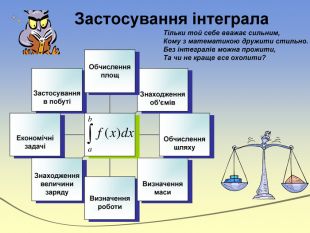
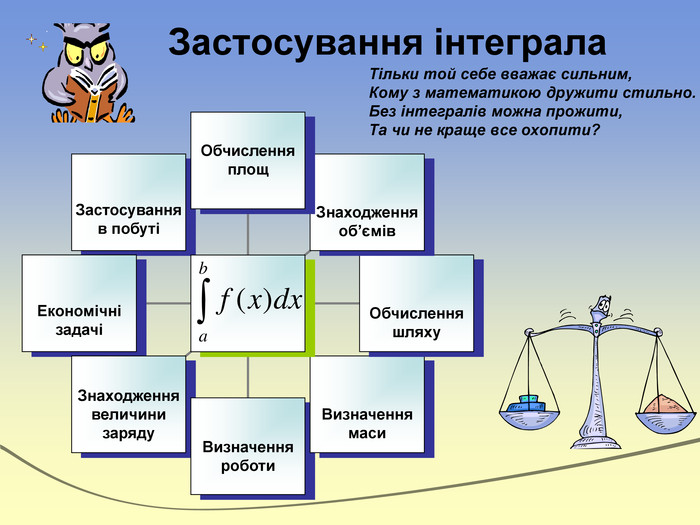
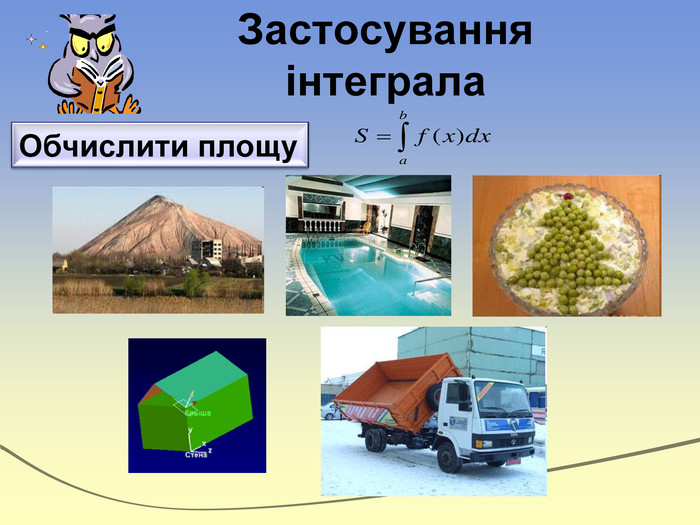
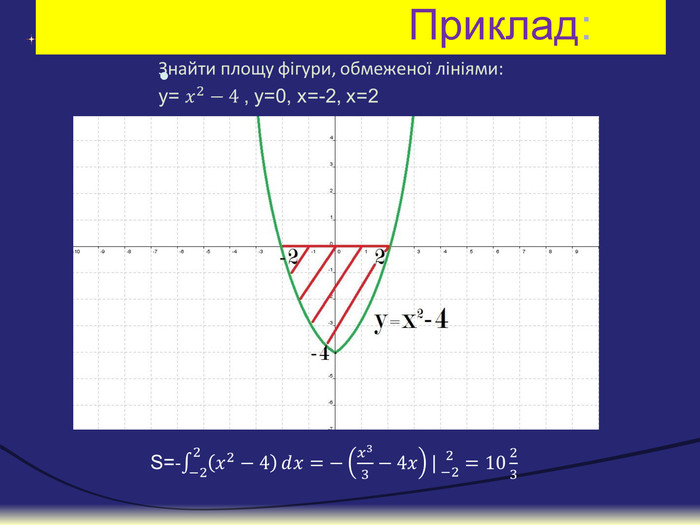
Застосування інтеграла. Тільки той себе вважає сильним,Кому з математикою дружити стильно. Без інтегралів можна прожити,Та чи не краще все охопити?Застосування в побутіЕкономічні задачіЗнаходження величини заряду. Визначення роботи. Визначення маси. Обчислення шляху. Знаходження об’ємів. Обчислення площ
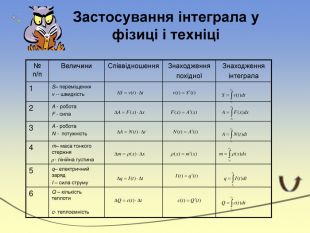
Застосування інтеграла у фізиці і техніці № п/п Величини Співвідношення Знаходження похідної Знаходженняінтеграла 1 S– переміщенняv -- швидкість 2 A - робота. F - сила 3 A - робота. N - потужність 4m– маса тонкого стержня - лінійна густина 5q– електричний заряд. I – сила струму 6 Q – кількість теплотиc- теплоємність
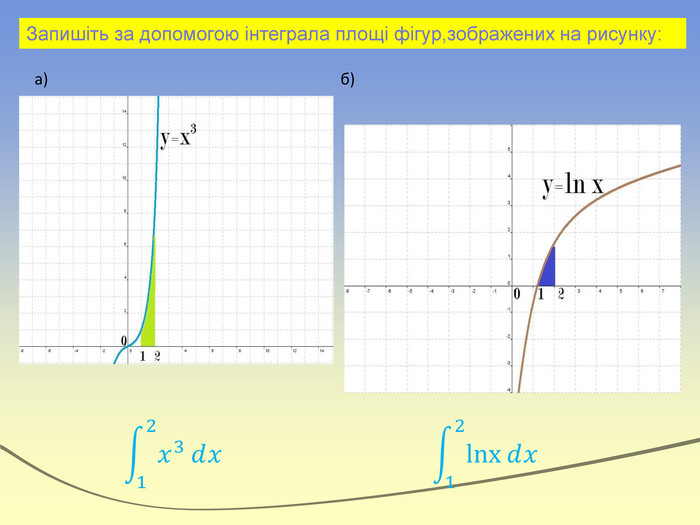
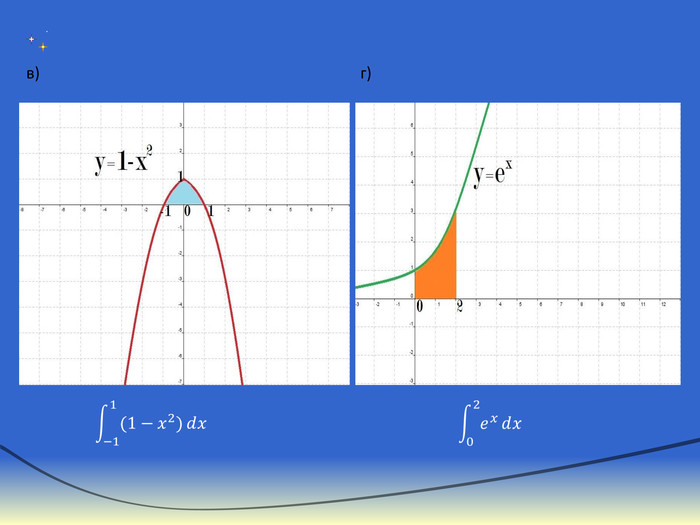
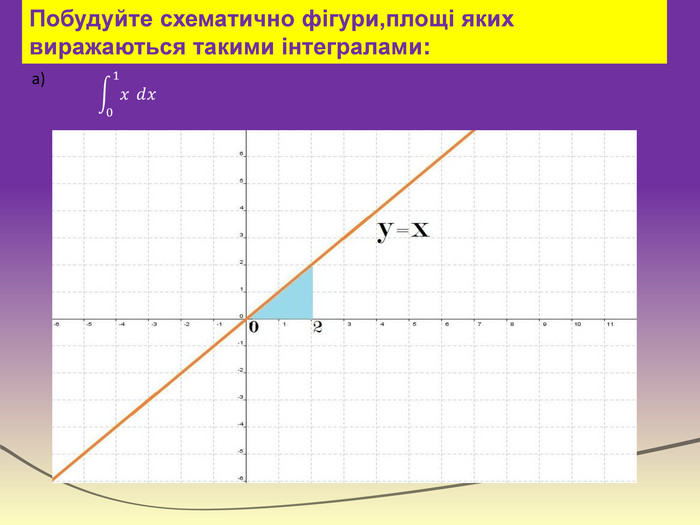
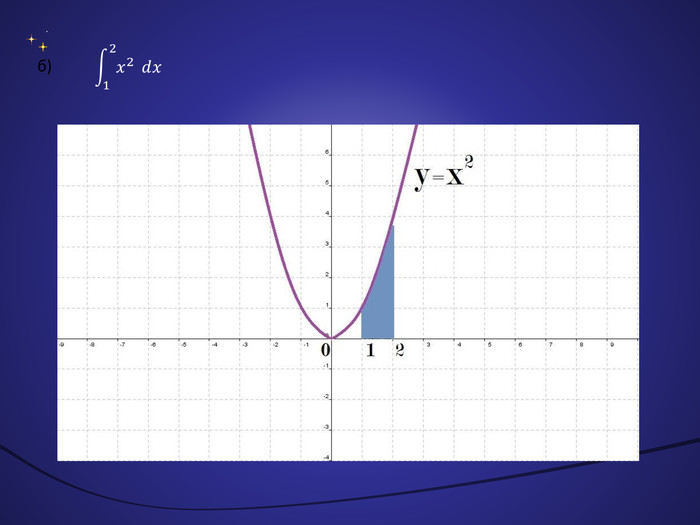
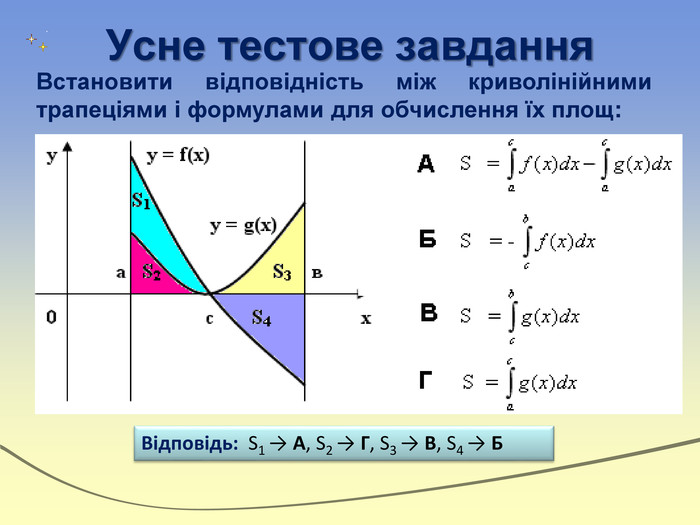
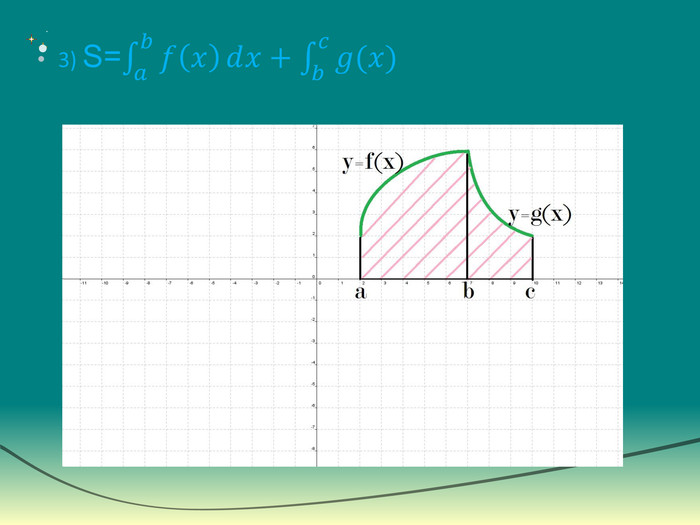
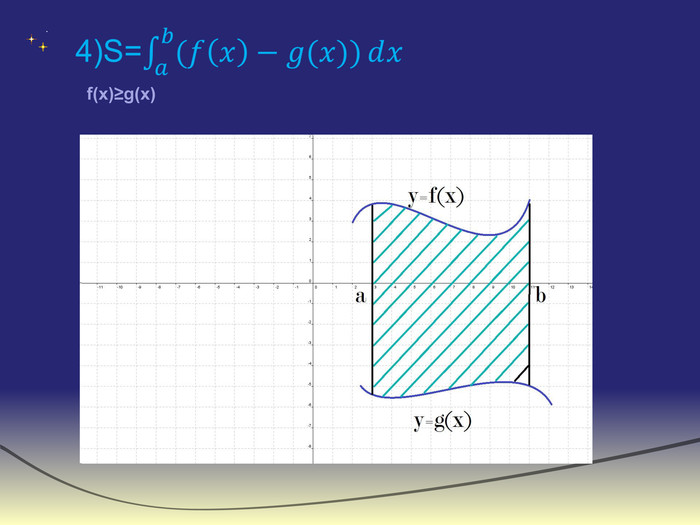
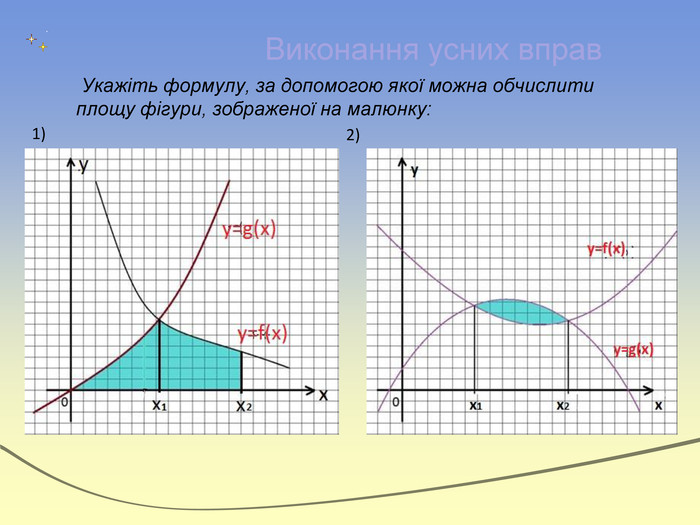
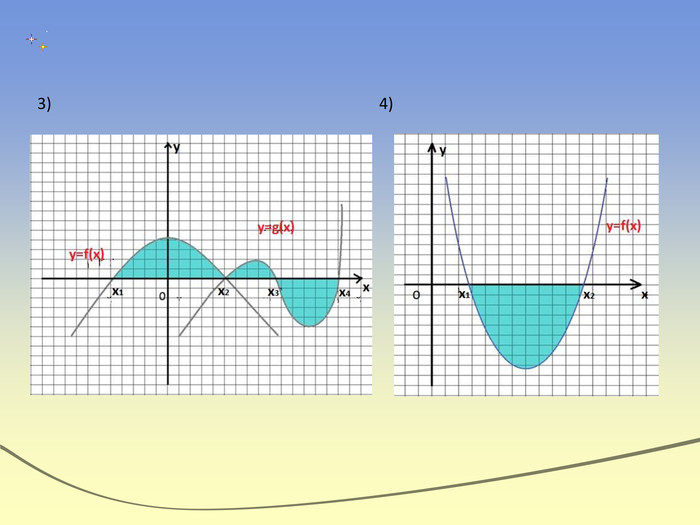
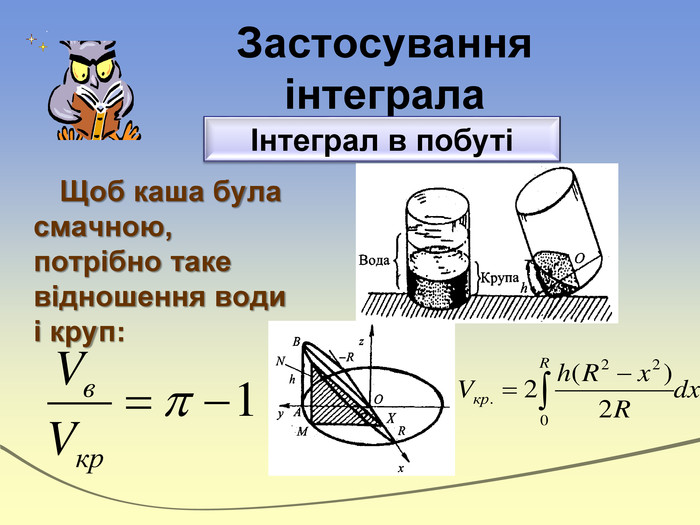
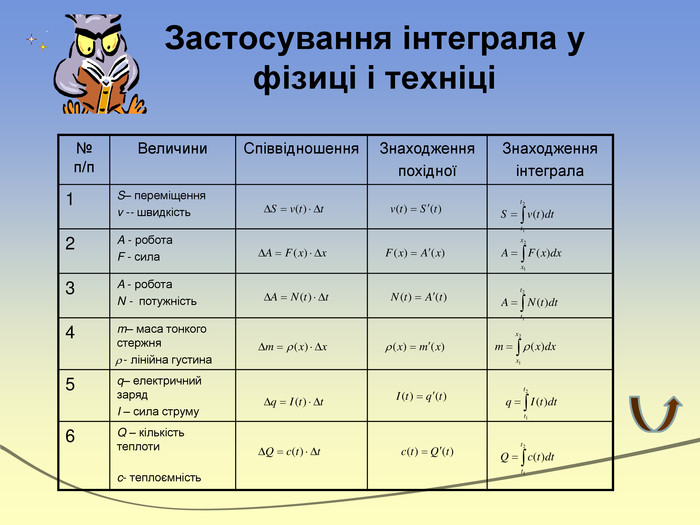
Експрес-опитування“Теоретичний марафон”Що таке первісна?Сформулювати основну властивість первісних. Що називають невизначеним інтегралом?Сформулювати означення визначеного інтеграла. Записати на дошці формулу Ньютона-Лейбніца і дати пояснення кожного символу. В чому полягає геометричний зміст визначеного інтеграла?Дати визначення криволінійної трапеції. Записати формулу для знаходження площі фігури,обмеженої зверху і знизу графіками неперевних функцій та прямими х=a і х=b (a
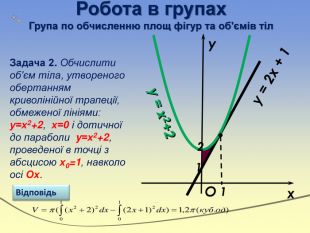
Робота в групах. Група по обчисленню площ фігур та об'ємів тіл. Задача 2. Обчислити об'єм тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями: у=х2+2, х=0 і дотичної до параболи y=х2+2, проведеної в точці з абсцисою х0=1, навколо осі Ох. Відповідьxyy = x2+2y = 2x + 1 O211
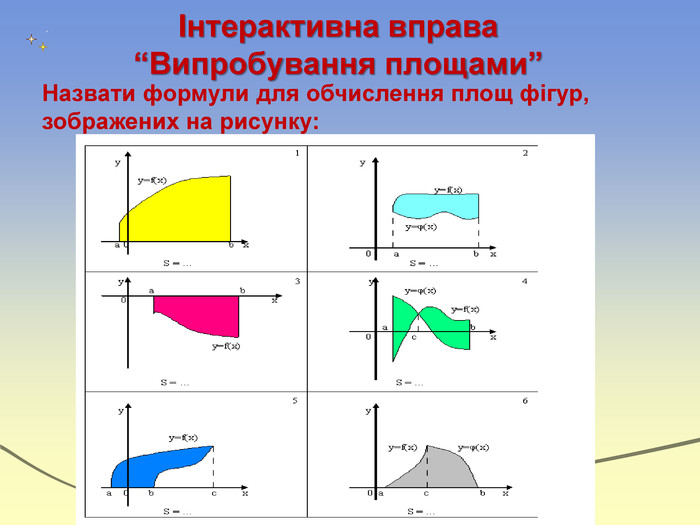
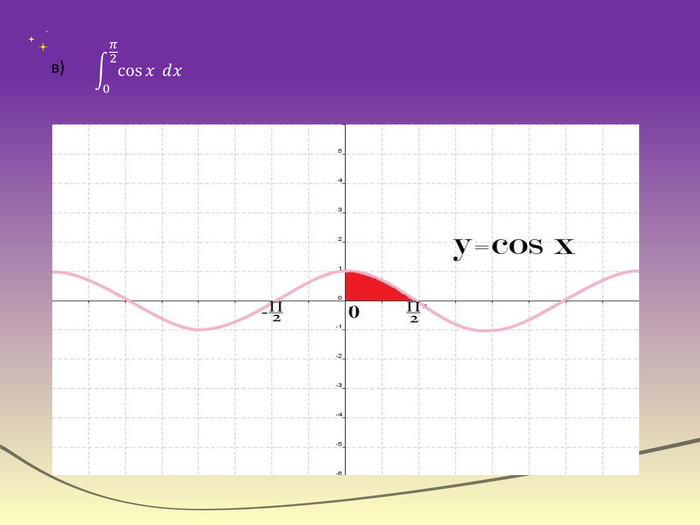
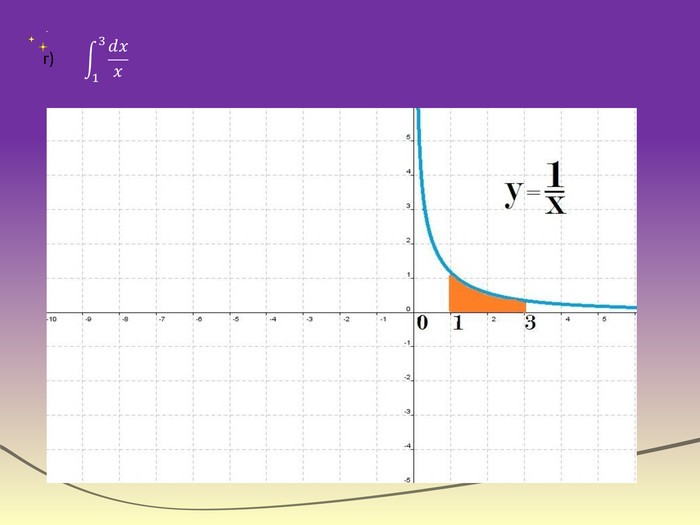
Робота в групах. Група по розв'язуванню задач фізичного змісту. Задача 1. Два тіла почали рухатися одночасно по прямій із однієї точки в одному напрямі. Одне тіло рухалось із швидкістю v1(t)=3t2+2t( м/с); друге-із швидкістю v2(t)=2t(м/с). Чому буде дорівнювати відстань між тілами через 6 с.?Відповідь: 216 м . Задача 2. З підручника №4, §26. Яку роботу потрібно витратити на стискання пружини на 4 см, якщо відомо, що сила 2 Н стискає цю пружину на 1 см?Відповідь: 0,16 Дж .
Робота в групах. Група по розв'язуванню нестандартних завдань. Задача 1. При яких значеннях S1 більше від S2 на 0,125 кв.од.?Відповідь: t=arcsin0,25. Задача 2. Знайти всі додатні числа a, для кожного з яких Відповідь: a=1. Задача 3. При якому значенні a пряма х=а ділить фігуру, обмежену графіком функції та прямими y=0, x=2,x=8 на дві рівновеликі частини?Відповідь: a=4.
Історія розвитку понять інтеграла й інтегрального числення пов’язана з потребою в знаходженні площ фігур, а також поверхонь і об’ємів довільних тіл. Передісторія інтегрального числення сягає глибокої давнини: ідеї інтегрального числення можна знайти в роботах давньогрецьких вчених Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда (бл.287-212 до н.е.).
Математики XVII ст. вчилися на працях Архімеда. Німецький астроном Й. Кеплер застосував подібні методи. Італійський математик Б. Кавальєрі, уявивши кожну фігуру утвореною з відрізка, а тіло із плоских фігур, сформулював принципи, які вважав очевидними й приймав без доведення. Символ ∫ - змінену латинську букву S (summa) – запровадив Г. Лейбніц, слово «інтеграл» - швейцарець Я. Бернуллі. Й. Кеплер. Г. Лейбніц. Я. Бернуллі
Слід зазначити, що в XVII ст. інтегрального обчислення як такого ще практично не було. Зв’язок між операціями диференціювання й інтегрування, узагальнення ідей, на яких ґрунтується розв’язання багатьох задач, було знайдено І. Ньютоном і Г. Лейбніцем: незалежно один від одного учені відкрили вираз, відомий зараз як формула Ньютона – ЛейбніцаІ. Ньютон


про публікацію авторської розробки
Додати розробку