Урок "Комбінаторні задачі. Класичне означення ймовірності."

Тема уроку: Комбінаторні задачі. Класичне означення ймовірності.

Мета уроку:

навчальна: сформувати уявлення про комбінаторику та комбінаторні задачі; розглянути приклади розв'язування найпростіших комбінатор­них задач;

розвивальна: : розвивати логічне мислення, кмітливість;

виховна: виховувати наполегливість.

Тип уроку: засвоєння нових знань і вмінь.

Хід уроку

I. Організаційний етап.

Перевірити готовність класу до уроку. Налаштування на роботу.

II. Перевірка домашнього завдання.

Поставити запитання до класу по темах вивчених на минулих урокам

III. Формулювання мети і завдань уроку.

Створити проблемну ситуацію, запропонувавши за­дачу практичного змісту.

У шкільній їдальні на сніданок можна вибрати булку, ватруш­ку, пряник або кекс, а з напоїв — чай, сік або молоко. Скільки різ­них варіантів сніданку можна вибрати?

Після цього повідомити, що ця задача належить до так званих комбінаторних. Вивчає способи розв’язання таких задач розділ математики, який має назву комбінаторика.

Отже, завдання уроку: зрозуміти, що вивчає комбінаторика, ознайомитися з деякими способами розв’язування комбінаторних задач.

IV. Сприймання і засвоєння навчального матеріалу.

Нехай дано n елементів.

1.  Всі впорядковані сукупності з n елементів називаються перестановками. Число перестановок із n елементів позначають 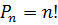, де
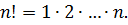
2.  Числом комбінацій із n елементів по k називається сполуки, кожна із яких містить k елементів взятих із даних n елементів, і відрізняється від іншої хоча б одним елементом. Число комбінацій обчислюється за формулою:

3.  Числом розміщень із n елементів по k називається сполуки, кожна із яких містить k елементів взятих із даних n елементів, і відрізняється від іншої або елементами або порядком елементів. Число розміщень позначається:

Подія – це результат випробування. Їх позначають: A, B, C, D .

Достовірною називається подія, яка при виконанні певних умов обов’язково відбувається в результаті випробування.

Неможливою називається подія, яка при виконанні певних умов ніколи не відбувається в результаті випробування.

Випадковою називається подія, яка може відбутися або ні в результаті випробування, вона залежить від багатьох випадкових факторів, які наперед врахувати неможливо.

Дві події А і В називаються рівноможливими, якщо при виконанні ряду умов однаково можливі появи подій А і В.

Дві події А і В називаються  єдино можливими якщо в результаті випробування обов’язково відбудеться одна і лише одна подія.

Ймовірністю події A називають відношення числа сприятливих появ події A до числа всіх несумісних рівно можливих і єдино можливих результатів випробування. Позначають , де n - число всіх можливих результатів випробування, а m - число сприятливих появ події A.

При статистичному означенні в якості ймовірності події приймають її відносну частоту

де m - число випробувань, в яких подія відбулася, n - загальне число проведених випробувань.                                      

Практично неможливою подією називається подія, ймовірність якої не в точності дорівнює нулю, але досить близька до нуля.

Практично достовірною подією називається подія, ймовірність якої не в точності дорівнює одиниці, але досить близька до одиниці.

Сумою двох подій А і В називають таку подію С, що відбувається тоді, коли відбувається або подія А, або подія В, або події А і В одночасно в одному експерименті. Суму подій А і В прийнято записувати в такий спосіб: .

Добутком двох подій А і В називають таку подію С, що відбувається тоді, коли відбувається і подія А, і подія В одночасно в одному експерименті. Добуток подій А і В прийнято записувати в такий спосіб: .

Дві події А і В називаються несумісними, якщо ніякі дві з них не можуть відбутися одночасно в одному експерименті.

Сумісними називаються події, якщо вони можуть відбутися в одному випробуванні.

Задача 1. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться число, кратне 3?

Розв’язання. Число всіх елементарних подій для цього експерименту . Нехай В — поява на грані числа, кратного 3. Число елементарних подій, що сприяють появі В, дорівнює двом

Отже,

Відповідь:

Задача 2. В популярній грі „Спортлото” учасник повинен назвати 5 видів спорту (5 чисел ) із 36. Яка ймовірність того, що вірно будуть названі 3 види спорту?

 Розв’язання.

Задача розв’язується за формулою математичної ймовірності події , де —подія , яка полягає в тому, що вірно буде названо 3 види спорту; —число всіх можливих випадків (шансів) при виборі 5 видів спорту із 36; —число випадків, які сприяють появі події

Загальне число всіх можливих випадків дорівнює числу комбінацій із 36 елементів (видів спорту) по елементів в кожній, тобто .Число сприятливих випадків для події , тобто того факту,що серед названих 5-ти видів спорту вірно будуть вибрані 3 види спорту , дорівнює добуткові числа випадків, якими можна вибрати 3 види спорту із 5 названих () на число випадків, якими можна вибрати 2 види (2=5-3) спорту із 31 неназваних видів (31=36-5) спорту (), тобто

.

Таким чином , шукана ймовірність визначається за формулою

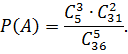
Використовуючи формулу для обчислення числа комбінацій

Одержимо,

Відповідь: Р.

Задача 3. Партія складається з 10 стандартних і 5 нестандартних деталей. Із партії навмання беруть 5 деталей. Знайти ймовірність того, що серед узятих деталей 3 виявились стандартними.

Розв’язання. Подія А — «серед 5 деталей 3 стандартні, а 2 нестандартні». Деталі беруться навмання, тому можливою елементарною подією є будь-яка група з 5 деталей, вибраних із 15 деталей. Щоб визначити, до якого типу підмножин належать ці групи, розглянемо одну з них. Нехай у групі виявилося 2 стандартні і 3 нестандартні деталі, тобто маємо . Виконаємо у групі довільне переставлення, наприклад . Група не змінилась — у ній як було, так і залишилося 2 стандартні деталі. Отже, порядок у групі неістотний, тому такі групи належать до комбінацій. Усі елементарні події рівноможливі, для обчислення ймовірності застосуємо формулу класичного означення ймовірності.

Загальна кількість елементарних подій

Щоб обчислити кількість елементарних подій, які становлять подію А, міркуємо так: 3 стандартні деталі з 10 можна вибрати способами, а 2 нестандартні з 5 —   способами. Отже,

Остаточно дістаємо:

Відповідь: 0,4.

Задача 4. В групі 15 студентів, серед яких 7 відмінників. По списку навмання вибирають 6 студентів. Знайти ймовірність того, що серед вибраних студентів будуть 4 відмінники.

Розв’язання. Нехай подія А – серед шести вибраних студентів 4 відмінники. Тоді,

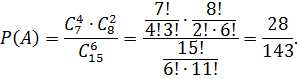
Відповідь:

Задача 5. У шухляді міститься 10 одинотипних деталей, 6 із яких є стандартними, а решта бракованими. Навмання із шухляди беруть чотири деталі. Обчислити ймовірність таких випадкових подій:

А — усі чотири деталі виявляються стандартними;

В — усі чотири деталі виявляються бракованими;

D — із чотирьох деталей виявляються дві стандартними і дві бракованими.

Розв’язання. Кількість усіх елементарних подій

кількість елементарних подій, що сприяють події А:

кількість елементарних подій, що сприяють появі В:

кількість елементарних подій, що сприяють появі D:

Обчислимо ймовірності цих подій:

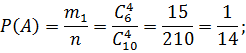
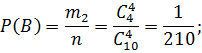
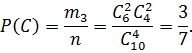
 V. Завдання для самостійного виконання

1. Два гральні кубики підкидають по одному разу. Знайти ймовірності таких подій:

А — сума цифр виявиться кратною 4;

В — сума цифр дорівнює 3.

2.               В урні міститься 5 білих, 3 чорних та 4 червоних кульки. Навмання виймають одну кульку. Знайти ймовірність того, що навмання вийнята кулька є червоною.
3.               З проміжку [0; 5] випадковим  чином вибирають два дійсних числа. Яка ймовірність того, що сума чисел дорівнює 5.
4.               У лотереї є всього 1000 квитків, з них 20 виграшних. Куплено два квитки. Визначити ймовірність того, що обидва квитки виграшні.
5.               Партія складається з 20 виробів, з яких 8 виробів 1-го сорту, 6—2-го, 2—3-го сорту, а решта — браковані. Навмання беруть 4 вироби. Знайти ймовірність того, що серед них виявилося 2 вироби 1-го сорту, 1—2-го сорту і 1 бракований.
6.               По цілі проведено 30 пострілів, причому зафіксовано 24 влучення.

Знайти відносну частоту влучення в ціль.