Интегрированный урок по математике и экономике в 9 классе по теме «Процентные расчеты. Формулы простых и сложных процентов»

 

 

 

 

 

Интегрированный урок по математике  и экономике

в 9 классе  в виде деловой игры «Я- клиент банка»

 

Тема урока: «Процентные расчеты. Формулы простых и сложных процентов»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Предмет: алгебра

Класс: 9

Учитель: Пасюга Ю.Ю.

Тема урока.  Процентные расчеты. Формула простых и сложных процентов.

Цели урока:

Образовательные цели:

- обобщить знания учащихся о процентах, повторить основные типы и способы решения задач на проценты;

- сформировать умения учащихся применять знания формул сложных процентов в разнообразных ситуациях;

- организовать деятельность учащихся по самостоятельному применению знаний и по самопроверке полученных знаний.

Развивающие цели: - развивать логическое мышление, творческие способности;

- развивать познавательный интерес учащихся к математике и экономике.

Воспитательные цели- воспитывать уважительные отношения друг к другу;

- воспитывать творческую, свободную и ответственную личность;

Тип урока: Комбинированный урок;

Оборудование и наглядность: презентация в Power Point, подборка задач на тему „проценты”, наглядные пособия;  раздаточный материал; карточки самооценивания.

Форма проведения: деловая игра «Я - клиент банка»

Ход урока

1. Организационный этап.

Проверить готовность учащихся к уроку, настроить их на работу.

Приветствие. Создание эмоционального фона.

2. Формирование цели и задач урока.

Мотивация учебной деятельности учеников. ( Слайд 1)

Учитель. Когда-то классик украинской литературы М.Рыльский сказал: „Новая жизнь нового стремится слова”. Я бы добавила, что не только слова, но и действий, профессий, нового мышления и мировоззрения в целом. Чтобы найти применение своим способностям и возможностям, надо уметь быстро адаптироваться в современном жизненном пространстве. Скоро вы покинете стены школы и перед вами остро встанет вопрос   выбора профессии.

Меня интересует знаете ли вы какие профессии сейчас наиболее востребованы, как развивается современный рынок труда?

       Конечно, вы правы, эти профессии очень нужны.  Именно вам, подростающему молодому талантливому поколению, предстоит поднимать нашу экономику, сделать Украину процветающим государством. Вне зависимости от выбранной профессии мы   являемся субъектами экономической деятельности, поэтому знание основных экономических понятий и законов необходимо любому человеку.  И любой грамотный современный человек должен знать математику.

Представьте себе такой случай. Мы живем теперь в XXI веке. Если бы кто-то из наших далеких предков, которые жили ровно 1000 лет назад, подумал бы положить в банк 1 копейку под 5% прибыли, то теперь эта копейка превратилась бы в большое богатство. Чтобы судить о величине этой суммы, представьте себе шар из чистого золота величиной с земной шар. Стоимость нескольких таких шаров и есть эта сумма, в которую выросла 1 копейка.                       

Поэтому сегодняшний интегрированный урок математики и экономики мы проведем в виде деловой игры, которую так и назовем „ Я- клиент банка”.

     Свой банк назовем „Будущее Украины” - в вашу честь, потому что вы - будущие хозяева украинской земли. Вот сегодня мы и убедимся в надежных ли руках будущее нашего государства.

 Итак, начинаем деловую игру. Как известно, в Украине денежная единица - гривна; в Европе - евро, а вы будете получать за свои знания (за правильные ответы) денежную единицу „проценто”,  так как  тема нашего урока  «Процентные расчеты. Формулы простых и сложных процентов».  Сегодня мы обобщим и систематизируем знания и умения по теме. До конца урока вам нужно пополнить банк денежной единицей „проценто” в виде ваших знаний.

Слоган нашого банка… Честным быть выгодно.  (слоган – это короткая фраза, передающая идеологию банка).  Поэтому я рассчитываю на вашу честность и порядочность.

Сегодня я буду генеральным директором нашого банка, а вы работать будете в группах- отделениях банка, которые назовем Отдел кредитов, отдел депозитов, отдел общей информации.

 Приступая к работе, а еще хочу сделать акцент.   «В любом деле без веры в собственную победу ничего не получится».

На своих карточках самооценивания на круговой диаграмме на сколько процентов  вы верите в себя.

Итак, давайте сначала разберемся что такое банк и как он работает.

3. Формирование новых знаний по теме «Банк»

Выступление учеников по теме, используя презентацию.  (Слайды 2-9)

(банк, функции и виды банков, денежная единица Украины)

Комментарии учителя.

4. Повторение теоретического материала (Слайды 10-16)

 (ответы на вопросы журналистов).  

  Наш банк „Будущее Украины” начинает свою работу. Для того, чтобы работа банка была понятной для всех клиентов, мы проведем сегодня пресс - конференцию для представителей средств массовой информации.

 

1) Газета „Банковское дело”

- У меня вопрос:  Объясните пожалуйста, что означает процент,  откуда пошло название „процент” и кому приходится часто решать задачи на проценты?

Почему необходимо понимать и уметь решать задачи на проценты?

Потому, что с задачами на процентные расчеты мы встречаемся в повседневной жизни. Приведем примеры:

 Повышение или снижение цен на товары;

 Объявления коммерческих банков, привлекающих средства населения на различных условиях;

 Процентные ставки по кредитам;

 Сведения о доходах по акциям предприятий и фондов;

 Уровень инфляции;

 Влажность воздуха;

 Концентрация вещества в смеси (растворе, сплаве)

Приведите еще примеры применения процентов в различных отраслях.

2) Журнал „История и право”

- Скажите, пожалуйста, как и откуда возник символ %?

Символ % возник в XV веке в Италии. Еще в XIII-XVI все учебники уделяли внимание процентному исчислению. Слово “процент” происходит от латинского pro centum, что означает “от сотни”. Первые таблицы на проценты составил Симон Стевин -  математик, механик и инженер из города Брюсе (Нидерланды).

Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.

Их используют для характеристики выполнения производственных планов, определение рост или снижение продуктивности труда. В процентах мы выражаем влажность воздуха, жирность молока, содержание соли в растворе, количество отсутствующих и присутствующих учеников в классе. Сейчас знания процента необходимое каждому человеку.

3) Телепередача „Успешный бизнесмен”

а) Сколько процентов составляют числа 0,28; 0,5; 0,248; 7.

б) Сколько процентов от одной гривны составляют 4 копейки,  15 копеек,  60 копеек, 1 гривна, 7 гривен.

4) Издательство „Экзамен без проблем”

- Какие существуют типы задач на проценты, привести примеры.

5) Газета „Экономика и мы”

 Как увеличить или уменьшить число а на р%. Привести примеры.

6) Издательство „Шпаргалка учеников” просит оказать помощь и объяснить какими способами можно решать задачи на проценты.

7) Газета „Капитал”

- Скажите, пожалуйста, в каких операциях применяется формула простых и сложных процентов.  Спасибо.

8) Газета „Аргументы и факты”

Я хочу провести тестирование всех присутствующих, чтобы больше узнать о сотрудниках банка.

5. Актуализация опорних умений (Слайд 17)

ТЕСТОВОЕ ЗАДАНИЕ: (ученики выполняют в группах на отдельных листах, результаты заносять в бланк ответов, для проверки  передают другой группе)

1) Сколько килограмм соли содержится в 30кг 5%-го раствора?

А)2;              Б)1,5;    В)3,      Г)2,5

2) 30% некоторого числа равна 18. Найти это число.

А)90; Б)48, В)30, Г)60

3) Сколько процентов составляет число 25 от числа 125?

А)10;   Б)15,   В)20,   Г)25

4) На сколько процентов увеличится периметр квадрата, если его сторону увеличить на 20%?

А)4;   Б)20;   В)2,2,   Г)1

5) Фирма „Радуга” платит рекламным агентам 5% от стоимости заказа. На какую сумму надо найти заказ, чтобы получить 2000 грн.

А)1000,  Б)145,  В)456,  Г)40000

6) В течение сентября 2018 года цена на сыр „Гауда” выросла на 30%, а в течение октября 2018 года  цена выросла  на 20%. На сколько процентов повысилась цена за 2 месяц

А)23,     Б)28,    В)56,   Г)76

 

Учитель. Проверим насколько правильную информацию вы дали представителю газеты „Аргументы и факты”. (Слайд 18)

Проверим решения задач варианта (задачи с решениями спроектированы на экран).

Вариант №1.

1) Сколько килограмм соли содержится в 30кг 5%-го раствора?

30•0,05=1,5(кг)       Б)1,5;

2) 30% некоторого числа равна 18. Найти это число.

18/30•100=60     Г)60

3) Сколько процентов составляет число 25 от числа 125?

25/125•100%=20%       В)20

4) На сколько процентов увеличится периметр квадрата, если его сторону увеличить на 20%?

1,2•а=4,8а, а-сторона квадрата

(4,8а-4а)/4а=0,8а/4а=0,2 (20%)

5) Фирма „Радуга” платит рекламным агентам 5% от стоимости заказа. На какую сумму надо найти заказ, чтобы получить 2000 грн.

2000:5*100=40000(грн.)

6) В течение сентября 2018 года  цена на сыр „Гауда” выросла на 30%, а в течение октября 2018 года - на 20%. На сколько процентов повысилась цена за 2 месяца?

X*1,3*1.2=1,56X

Полученные ответы отметить в бланке

 

6. Формирование умений и навыков (слайд 19)

Учитель.  Мы убедились, что в нашем банке работают грамотные и компетентные сотрудники. Напоминаю, что главная функция банка - это работа с клиентами - выдача кредитов и прием денег на депозит.

Привлечения средств на депозит и выдача кредитов осуществляется по определенной процентной ставке. Процент - это средство стимулирования привлечения вкладов (депозитов) в банк и это так называемое вознаграждение банка за выдачу кредитов.  Порядок начисления и выплаты процентов, размер процентной ставки по депозиту или кредиту оговариваются в депозитном или кредитном договоре.  Для того, чтобы подсчитать банковские проценты существуют 2 типа задач и соответственно 2 формулы:

1) задачи на простые проценты;

2) задачи на сложные проценты.

Учитель. Предоставляем слово отделу депозитов. (Слайды 20-21)

Ученик.  Задача на простые проценты.

Если человек не вносит своевременную плату за что-нибудь, то на нее может налагаться штраф - «пеня». Допустим пеня составляет 1% от суммы платы за каждый день просрочки. Тогда, например, за 20 дней просрочки сумма пени составит 20% от суммы платы. И со 100 грн человек должен будет внести пеню 100 • 0,2 = 20 грн, то есть всего заплатить 120 грн.

В разных случаях, для разных людей сумма платы, время просрочки и пеня разные. Поэтому возникает необходимость составить формулу оплаты, которую можно использовать при различных обстоятельствах.

Этой формулой пользуются и банковские сотрудники, когда процентное начисление осуществляется ежемесячно(слайд)

Эта формула описывает много конкретных ситуаций и называется формулой простого процентного роста или формулой простых процентов.  Формулой простых процентов пользуются тогда, когда каждый последующий процент начисляется на первоначальную величину.

Мы предлагаем решить такую задачу на депозит.

Задача. При какой процентной ставке на месяц вклад на сумму 1000 грн увеличится за год до 1480 грн ?

Используем формулу простого процентного роста. Подставим вместо Sп величину конечной суммы - 1480, вместо S величину первоначального вклада - 1000 и вместо п количество месяцев - 12.

Получим и решим уравнение: 1480 = 1000(1 + 0,01•12•г); 1480 = 1000 + 120р; 120р = 480; р = 4.

Следовательно, процентная ставка должна составлять 4% в месяц.

Учитель. Предоставляем слово отделу кредитов. (Слайды 22-23)

Ученик.  Задача на сложные проценты.

В банках для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем, скажем, через год) принята такая система начисления: за первый год пребывания вложенной суммы в банк на счет начисляется, например, 18% от нее. Если в конце года вкладчик не снял со счета эти деньги - «проценты», как их обычно называют, то они присоединяются к вложенной сумме и в конце второго года 18% начисляются уже с увеличенной суммы. В данном случае «проценты начисляются на «проценты».

Это формула сложного процентного роста или формула сложных процентов.

Отличие простого процентного роста и сложного процентного роста заключается в том, что при простом росте процент каждый раз исчисляют, исходя из первоначального значения величины, а при сложном росте процент исчисляется от предыдущего значения.

Задача. Какая сумма будет на срочном вкладе через 4 года, если банк начисляет 10 % годовых и внесенная сумма равна 2000 гривен?

Учитель. Предоставляем слово отделу общей информации. (Слайд 24-25)

А теперь рассмотрим задачи на проценты, которые уже нельзя отнести к простейшим.

Задача. Вкладчик положил в банк на 2 разные счета 1 200 грн. За 1-ый счет банк выплачивает 6% годовых, а за 2-ой 8% годовых. Через год клиент получил 80 грн. процентных денег. Сколько гривен он положил на каждый счет?

 

Задача. Цену товара сначала снизили на 20%, потом новую цену снизили еще на 10% и, наконец, после пересчета провели снижение еще на 5%. На сколько процентов всего снизили начальную цену товара?

Ответ: На 31,6%.

 

У доски работают представители всех групп, решая задачи.

7. Подведение итогов урока

На уроке вы хорошо работали, продемонстрировали знания, активность, хорошо мыслили. Сегодня мы не только решали задачи на проценты, но и пополнили свой багаж знаний новыми экономическими понятиями. А насколько хорошо вы их усвоили, мы проверим, отгадав экономический кроссворд.

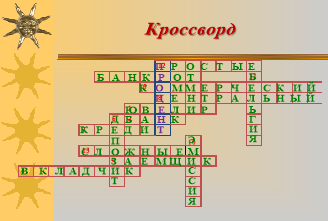Кроссворд (Слайд 26)

1. Первые банкиры в истории (ювелиры)
2. Учреждение, которое продает и покупает деньги (банк)
3. Разбитая лавка (в переводе с итал.) – банкрот
4. Как называется клиент банка, который кладет деньги в банк (вкладчик)
5. Как называется клиент банка, который берет деньги из банка под проценты (заемщик)
6. Деньги, которые мы кладем в банк (депозит)
7. Деньги, которые мы берем из банка (кредит)
8. Как называется главный банк страны (центральный)
9. Какой банк осуществляет работу с клиентами (коммерческий)
10. Печатание денег(эмиссия)
11. Страна ученого, который первый опубликовал таблицу процентов (Бельгия)
12. Как называются проценты, которые начисляются только на первоначальную сумму (простые)
13. Как называются проценты, которые начисляются на предыдущее значение (сложные)

Мы получили проверочное слово – ПРОЦЕНТ, а значит правильно разгадали кроссворд.

    Рефлексия

• Упражнение «Незаконченные предложения»

Учитель:    На сегодняшнем уроке я узнал...

                    На сегодняшнем уроке важнейшим открытием для меня было...

                    В начале урока я поставил перед собой цель…

• Диаграмма

В своих карточках самооценки отметьте на сколько процентов вы работали на уроке, на сколько процентов вы удовлетворены своими успехами.

8. Оценивание учеников

Каждая группа подсчитывает заработанные баллы- денежную единицу «проценто», отмечают тех, кто более активно принимал участие на уроке.

9. Домашнее задание.

Повторить формулу процентных расчетов.

Выполнить дифференцированное домашнее задание (разноуровневые задания по выбору учеников)