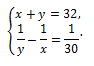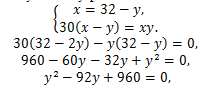Презентація з теми"Розв'язування системи рівнянь другого степені"; Конспект уроку з теми:"Розв'язування системи рівнянь другого степені"
Розробка уроку з алгебри у 9 класі.
Тема уроку: « Системи рівнянь другого степеня з двома змінними»
Мета уроку: повторити, систематизувати, й узагальнити знання та вміння учнів при розв’язуванні систем рівнянь з двома змінними графічним та аналітичним способами; складати системи рівнянь відповідно до умови задачі; стимулювати розвиток логічного мислення, творчих здібностей; формувати здатність аналізувати, узагальнювати, робити висновки.
Тип уроку: систематизація та узальнення знань та вмінь.
Обладнання:пам’ятка для учнів, картки із завданнями для самостійної роботи, тести, картки с завданнями для роботи в групах.
Хід уроку
Епіграф уроку: Мало знати, потрібно й використовувати.
Мало бажати, потрібно й робити. Й.Гете (слайд 5)
І Організаційний етап( Слайд2)
Учитель: Сьогодні ми на уроці вдосконалимо та закріпимо знання з теми системи рівнянь другого степені. Розглянемо різні способи розв'язування систем. Кожному хочу побажати успіху. Складається він з того, яким хоче бути кожен з вас тобто
У – успішним
С – спокійним
П – прогресивним
І – ініціативним
Х – хоробрим
Я бажаю вам успіху . І не тільки на уроках математики, бо якщо звернутися до слів філософа Е. Ільєнкова ,то можна зазначити «Усе людське життя – це не що інше, як постійна постановка та бажання досягти успіху під час розв'язування все нових питань та проблем». Підниміть руки, хто бажає досягти успіху? Я теж бажаю досягти успіху. Сподіваюсь, що сьогодні на уроці нас з вами чекає успіх. Всі ми покажемо свій розум, кмітливість.
ІІ. Мотивація навчальної діяльності( Слайд 3)
Ващ клас у 2021 році буде складати обов'язково ЗНО з математики. У програмі ЗНО є тема системи рівнянь. Щороку учням пропонуються завдання з цієї теми. Тому вивчати дану тему є надзвичайно важливою.
ІІІ.Повідомлення теми уроку та очікування результатів навчальної діяльності (Слайд4)
Сьогодні у нас урок з теми «Системи рівнянь другого степеня з двома змінними». У ході уроку ми, повторимо основні факти, які засвоїли, систематизуємо їх, та закріпимо вміння застосовувати знання під час розвязування вправ та задач.Тож будьмо уважними,активними,думаймо, пропонуймо, аналізуймо.Я сподіваюсь на успішну працю, і впевнена що на уроці ви зможете виявити знання, вміння , кмітливість. Записали число та тему урока. (Слайд 5)
ІV. Повторення та систематизація знань учнів (Слайд 6)
Усне опитування «Хай живе теорія!» технологія «Мікрофон» (5хв)
- Що таке система рівнянь другого степені?( якщо одне рівняння системи другого степеня, а друге з тими самими змінними другого або першого степеня, то таку систему називають системою двох рівнянь другого степеня з двома зміннішії.)
- Що є розв'язком системи рівнянь другого степені?(пара чисел, яка при підстановки в систему перетворює кожне рівняння в вірні рівності)
- Що позначає розв'язати систему рівнянь?(знайти все рішення або довести що їх немає)
- Які способи розв'язування рівнянь?( графічний та аналітичні)
- У чому суть способу додавання? ( коефіцієнти при одній змінної є протилежні числа)
- У чому суть способу підстановки? ( в заміні даної системи рівнянь рівносильної системою, в який одне з рівнянь має одне невідоме)
- Що є графіком рівняння
х²+у²=16, х-3у=1, ху=5, (х-1)²+(у+3)²=9, у=√х, у = 3 х2+5.
- Виразіть одну змінну через іншу
1) 2х+у=12 2) 5х-у=1 3) ху=-1 4)у-х²+5=0
Висновок: Повторіли теоретичний матеріал.
Тестові завдання (6хв)
1. Графік якого рівняння зображений на рисунку
А) х2 + у2 =4; б) ху = 4;
В) у = 2х2; г) у = 2х+5.
2. Яка пара чисел є розвязком систем х2 + у2 =10 А)(3;1); б)(3;-1); в) (-3;-1)
2х+у = 5
3. Які фігури є графіками системи рівнянь х2 + у2 =5
ху = 3
а) пряма і парабола; б) коло і парабола; в) коло і гіпербола; г) парабола і гіпербола.
4. Встановить співвідношення:
|
|
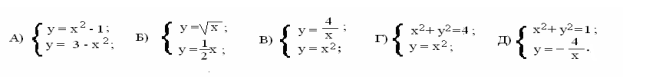
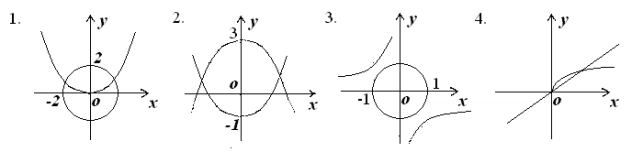
А |
Б |
В |
Г |
Д |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
V. Розв’язування систем рівнянь(робота в парах) (слайд 7)
І ряд
Розв'язати графічно систему рівнянь: у = х2 + 2
у – х = 4 Відповідь: (-1;3); (2;6)
Чому цій спосіб не зручний? (громоздкий, не завжди у відповіді цілі числа)
Коли зручно використовувати цій спосіб? (коли треба узнати скільки коренів має система рівнянь)
ІІ ряд
Розв'язати систему рівнянь методом підстановки: х – у =2
у2 – 2ху = 3
х = у+2 у1 = -3 у2 = -1
у2+ 4у + 3 = 0, х1 = -1 х2 = 1
Відповідь: (-1; -3); (1;-1)
Коли зручнише використовувати цій способ? (коли коефіцієнт при будь - якій змінній у рівнянні дорівнює 1)
ІІІ ряд Розв'язати систему рівнянь методом додавання:
х2 – у = 7 2х2 = 18 х2 =9 х1 = 3 х2 = -3
х2 +у = 11 х2 – у = 7 у = 2 у1 = 2 у2 =2 Відповідь: (3;2); (-3; 2)
Учитель Слайд(8,9,10) Презентація. Знаменитий французький математик Франсуа Вієт народився в 1540р. у містечку Фонтеней. Його батьки мріяли, що син стане адвокатом. Після закінчення юридичної школи у 1559р. Вієт почав свою адвокатську діяльність. Він вів справи однієї дворянки і водночас навчав астрономії її єдину дочку Катерину. Навчаючи дівчину, Франсуа і сам захопився астрономією. У нього виникає задум створити велику працю з астрономії. Щоб написати її, потрібні були знання з тригонометрії, тому Вієт сумлінно починає працювати і над вивченням математики. Через свою ученицю Франсуа познайомився з Генріхом Наварським і згодом став його радником.
У 1671р. Вієт приїжджає до Парижа, щоб особисто познайомитись з паризькими математиками.
Розповідають, що нерідко, забувши про їжу, Франсуа міг дві – три доби підряд просиджувати за своїм робочим, розв’язуючи якусь цікаву задачу, або досліджуючи якесь складне питання.
Вієт розробив ряд важливих питань теорії рівнянь 1- 4 степенів. Він сформулював і довів кілька теорем про взаємозв’язки між коренями і коефіцієнтами рівняння, зокрема й теорему про зведене квадратне рівняння.
Вієт активно застосовував свої знання не лише в галузі алгебри і геометрії. Відомо, наприклад, що він любив розгадувати зашифровані листи. Під час війни з Іспанією всі таємні листи іспанців вільно читали французи. Як не намагалися іспанські шифрувальники заплутати шифр, Вієт щоразу розгадував його В останні роки свого життя Вієт обіймав важливі посади при дворі короля Франції. Помер у Парижі 1603 р.
Задачі, що зводяться до системи рівнянь з двома змінними уміли розв’язувати китайські математики понад дві тисячі років тому.
Давньогрецький математик Діофант знаходив натуральні розв’язки більш складних систем рівнянь.
Графічний спосіб рівнянь вперше запропонував видатний французький філософ, математик, фізик, фізіолог Рене Декарт.
Творчі завдання:( Слайд 11) 1. Скільки розв'язків має система рівнянь залежно від
значення а?
х2 + у2 = 4
у = а
Відповідь: Якщо а =2 або -2 один розв'язок, якщо -2
а2 – два розв
язка,
якщо а
розв'язків немає
V. Самостійна робота (різнорівнева)(слайд 12)
І варіант ІІ варіант
1. Розв'язати систему рівнянь методом підстановки:
х2 – у = 8 у – х = -1
х + у = 4 х2 +2у = 6
2. Розв'язати систему рівнянь методом додавання:
х + у2 = 3 х + у2 = 7
х - у2 = 1 2х - у2 = 2
Відповіді: варіант1 1) (-4; 8) , (3;1) 2) (4;3), (-2;-3)
Варіант 2 1) (2;1), (2; -1) 2) (3;2), (3;- 2)
VІ. Підсумок уроку: (Слайд 13,14)
Кросворд: (робота в парах)
1. Автор підручника алгебра 9 класу.
2. Назва графіка квадратичної функції.
3. Графік рівняння х2 + у2 =9.
4. Один зі способів розв'язування систем рівнянь.
5. В честь якого вченого названа координатна площина.
6. Залежність у від х .
7. Зображення функції f(х)
Отримали слово «Молодці»( Слайд 15)
Рефлексія
Зверніть увагу на малюнок намальований на дошці. На початку уроку всі були на першій сходинці, а зараз кожен для себе визначить на якій сходинці він зараз.
VІ. Домашнє завдання: (Слайд 16)
1) повторити алгоритми розв'язування систем рівнянь
2) стор. 146 тести (№7-9-середній рівень, №7-10 – достатній рівень, №7-11 – високий рівень)
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
24 серпня 2001 року в Харкові відкрили пам'ятник футбольному м'ячу. На постаменті із чорного граніту установлено м'яч діаметром 1,5 метра. Загальна вага споруди більше 2 тонн (Рис.1.).
Рис.1.
В 1999 році найкращим футболістом світу був визнаний бразилець Ривалдо (Рис.2.). Отримавши приз "Золотий м'яч", він розпиляв його на 60 частин, прикріпив до кожної срібну пластину зі своїм ім'ям. Ці оригінальні подарунки спортсмен роздав тим, кого вважав причетними до свого успіху: товаришам по команді, тренерам , командному лікарю і масажисту і навіть прибиральниці стадіону.
Рис.2. Ривалдо
IV. ЗАСТОСУВАННЯ ЗНАНЬ, ФОРМУВАННЯ ВМІНЬ І НАВИЧОК
Задача 1. Сучасний м'яч виготовляють зі шкіряних шестикутників і п'ятикутників, які сполучають між собою для надання м'ячу круглої форми (рис.3.). Кількість цих шестикутників і п'ятикутників дорівнює 32, різниця чисел, обернених до кількості п'ятикутників і шестикутників, — 1/30 . Знайдіть кількість п'ятикутників і шестикутників, з яких виготовляють футбольний м'яч.
Розв'язання. Нехай х — кількість шестикутників, у — кількість п'ятикутників. Відомо,що сума цих чисел дорівнює 32, а різниця чисел, обернених до
попадання — 1/30, x>y.
Рис.3.Футбольний м'яч
Розв'язування цієї задачі зводимо до розв'язування системи рівнянь другого степеня з двома змінними:
Оскільки х і у не дорівнюють нулю, то після зведення до спільного знаменника у другому рівнянні дістанемо таку систему рівнянь:
звідки y1=12 або y2=80. .
За змістом задачі кількість п'ятикутників не може дорівнювати 80. Тоді
х=32-12=20.
Відповідь. 20 шестикутників і 12 п'ятикутників.
Слід зазначити, що п'ятикутники чорного кольору, шестикутники — білого. Чорні п'ятикутники допомагають більш тонко відчувати будь-які відхилення під час польоту м'яча.
ТЕМА: Розв’язування задач за допомогою складання систем рівнянь другого степеня з двома змінними
Антипіна Олена Вікторівна
Вчитель математики
ВУФК
м.Миколаїв
Класс: 9
Мета уроку:
- формувати вміння розв'язувати задачі за допомогою складання систем рівнянь другого степеня;
- повторити методи розв'язання систем рівнянь другого степеня;
- формувати вміння самостійно мислити;
- формувати пізнавальний інтерес,культуру мислення,мовлення
- збуджувати допитливість;
- ознайомити зі спортивним та культурним життям країни, міста.
Тип уроку:застосування знань, умінь, навичок.
ХІД УРОКУ
I. МОТИВАЦІЯ ВИВЧЕННЯ ТЕМИ
Учитель. Системи рівнянь другого степеня є математичною моделлю, що використовують для розв'язування практичних задач. Уміння розв'язувати задачу є мистецтвом, що здобувається практикою, подібно, скажімо, до спорту. Ми опановуємо будь-яку майстерність за допомогою наслідування та досвіду. За допомогою постійних, наполегливих,часто виснажливих тренувань, ви опановуєте спортивне мистецтво . Навчаючись розв'язувати задачі, ви повинні спостерігати і наслідувати інших у тому, як вони це роблять, і нарешті, ви опануєте це мистецтво, виконуючи відповідні вправи.
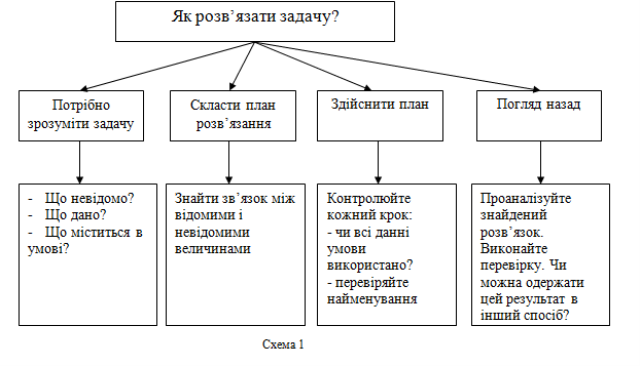
I I . ФОРМУЛЮВАННЯ АЛГОРИТМУ РОЗВ'ЯЗАННЯ ЗАДАЧІ ЗА ДОПОМОГОЮ СИСТЕМИ РІВНЯНЬ
(Дивись схему1.)
Рефлексія проводиться у формі інтерактивної вправи «Незакінчене речення»:
- Сьогодні на уроці я пригадав…
- Найбільш складним для мене було…
- Більше всього мені сподобалось…
- Мені сподобалось ( чи не сподобалось ) працювати в групі, бо…
- Я розвинув своє вміння…
- Тепер я буду більш успішним, бо…
- Мене влаштовує ( чи не влаштовує ) результат, бо…
- Я хотів би побажати…
4. Наш урок підійшов до кінця. Я вдячна Вам за співпрацю. Бажаю Вам успіхів. Пам’ ятайте слова Ломоносова:
«Все, що було темним, сумним і невірним, математика зробила ясним, вірним і очевидним
Варіант1
1. Графік якого рівняння зображений на рисунку
А) х2 + у2 =4; б) ху = 4;
В) у = 2х2; г) у = 2х+5.
2. Яка пара чисел є розвязком систем х2 + у2 =10 а) (3;1); б)(3;-1).
2х+у = 5
3. Які фігури є графіками системи рівнянь х2 + у2 =5
ху = 3
а) пряма і парабола; б) коло і парабола; в) коло і гіпербола; г) парабола і гіпербола.
4. Встановить співвідношення:
1) у= х2 – 1 2) у= 
3) у = 
4) х2 + у2 =4
у = 3 – х2 у = 
х у= х2 у = 2х2
а) б) в) г)
Варіант 2
1. Графік якого рівняння зображений на рисунку
А) х2 + у2 =4; б) ху = 4;
В) у = 2х2; г) у = 2х+5.
2. Яка пара чисел є розвязком систем х2 + у2 =4 а)(2;0); б)(0;-2).
х+у = 2
3. Які фігури є графіками системи рівнянь х2 + у2 =16
У = 5х-3
а) пряма і коло; б) коло і парабола; в) коло і гіпербола; г) парабола і гіпербола.
4. Встановить співвідношення:
1) у= х2 – 1 2) у= 3) у = 4) х2 + у2 =4
у = 3 – х2 у = х у= х2 у = 2х2
а) б) в) г)
Спосіб додавання
- Урівнюємо коефіцієнти при одній із змінних шляхом почленного множення обох рівнянь на відповідним чином підібрані множники;
- Додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну із змінних;
- Розв’язуємо одержане рівняння з однією змінною;
- Підставляємо найдене значення змінної в будь-яке із заданих рівнянь системи;
- Записуємо відповідь.
Спосіб підстановки
- Із одного рівняння системи виражаємо одну із змінних через другу змінну і відомі величини;
- Знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;
- Розв’язуємо одержане рівняння і знаходимо значення цієї змінної;
- Підставляючи знайдені значення у вираз для першої змінної, одержуємо відповідні її значення;
- Записуємо відповідь.
Графічний спосіб
1) Виразити у через х;
2) Побудувати в одній системі координат графіки рівнянь системи.
3) Визначити координати точок перетину графіків – саме вони є розв’язками.
4) Виконати перевірку.
5) Записати відповідь.
1. Розв'язати способом підстановки систему рівнянь:
Х2 - У = 8
Х + у = 4.
2. Розв'язати способом додавання систему рівнянь:
Х2 - У = 7
Х2 + У = 11.
1. Розв'язати способом підстановки систему рівнянь:
Х2 - У = 8
Х + у = 4.
2. Розв'язати способом додавання систему рівнянь:
Х2 - У = 7
Х2 + У = 11.
1. Розв'язати способом підстановки систему рівнянь:
Х2 - У = 8
Х + у = 4.
2. Розв'язати способом додавання систему рівнянь:
Х2 - У = 7
Х2 + У = 11.
1. Розв'язати способом підстановки систему рівнянь:
Х2 - У = 8
Х + у = 4.
2. Розв'язати способом додавання систему рівнянь:
Х2 - У = 7
Х2 + У = 11.
1. Розв'язати способом підстановки систему рівнянь:
У = 4Х
Х2 + У +3 = 0.
Вказівка: Підставити в друге рівняння замість у вираз 4х і розв'язати
квадратне рівняння.
2. Розв'язати способом додавання систему рівнянь:
Х – У2 = 1
Х + У2 = 3.
Вказівка: Перейти до системи додав рівняння.
1. Розв'язати способом підстановки систему рівнянь:
У = 4Х
Х2 + У +3 = 0.
Вказівка: Підставити в друге рівняння замість у вираз 4х і розв'язати
квадратне рівняння.
2. Розв'язати способом додавання систему рівнянь:
Х – У2 = 1
Х + У2 = 3.
Вказівка: Перейти до системи додав рівняння.
1. Розв'язати способом підстановки систему рівнянь:
У = 4Х
Х2 + У +3 = 0.
Вказівка: Підставити в друге рівняння замість у вираз 4х і розв'язати
квадратне рівняння.
2. Розв'язати способом додавання систему рівнянь:
Х – У2 = 1
Х + У2 = 3.
Вказівка: Перейти до системи додав рівняння.
Розв'язати способом додавання систему рівнянь:
Х2 – 2У = 7
Х2 + 2У = 11.
Розв'язати способом додавання систему рівнянь:
Х2 – 2У = 7
Х2 + 2У = 11.
Розв'язати способом додавання систему рівнянь:
Х2 – 2У = 7
Х2 + 2У = 11.
Розв'язати способом додавання систему рівнянь:
Х2 – 2У = 7
Х2 + 2У = 11.
І варіант Розв'язати способом додавання систему рівнянь:
Х2 – 2У = 7
Х2 + 2У = 11.
ІІ варіант
1. Розв'язати систему рівнянь методом підстановки:
х2 – у = 8 у – х = -1
х + у = 4 х2 +2у = 6
2. Розв'язати систему рівнянь методом додавання:
х + у2 = 3 х + у2 = 7
х - у2 = 1 2х - у2 = 2
Тема: Розв’язування систем рівнянь другого степеня з двома
змінними.
Математична прес - конференція
Мета:
навчальна: узагальнити і систематизувати способи розв’язування систем рівнянь, формувати вміння і навички досліджувати і розв’язувати системи рівнянь другого степеня з двома змінними;
розвивальна: розвивати пізнавальну компетентність, логічне мислення, увагу, пам'ять, спонукати учнів до творчої активності, ініціативи, прагнення досягати високих результатів ;
виховна: виховувати в учнів дисциплінованість, наполегливість, уважність, кмітливість; любов до предмета; самокритичність .
Тип уроку: узагальнення і систематизація знань, умінь і навичок.
Саніна Ніна Олексіївна,
учитель математики
Харківської загальноосвітньої школи
І – ІІІ ступенів № 129
Харківської міської ради
Харківської області
Алгебра . 9 клас.
Тема: Розв'язування систем рівнянь другого степені.
Очікувані результати навчально – пізнавальної діяльності учнів:
Знаннєвий компонент:
Називає графіки функцій, методи розв'язування систем рівнянь.
Діяльнісний компонент:
Застосовує різні способи розв'язування систем рівнянь;
Дотримується правил безпеки при роботі з інструментами;
Уміє ефективно співпрацювати самостійно та з іншими.
Ціннісний компонент:
Висловлює власну думку;
Виявляє соціальну активність, відповідальність.
Ключові компетентності уроку: спілкування рідною мовою,
пізнавальна компетентність, інформаційно – цифрова компетентність,
соціальна компетентність, загальнокультурна компетентність,
здоров'язбережувальна компетентність.
Тип уроку: систематизація та узагальнення знань та вмінь.
Хід уроку:
І. Організаційний етап.
Кожному хочу побажати успіху. Складається він з того, яким хоче бути
кожен з вас тобто
У – успішним
С – спокійним
П – прогресивним
І – ініціативним
Х – хоробрим
Я бажаю вам успіху!
ІІ. Мотивація навчальної діяльності учнів.
Ваш клас у 2021році буде складати обов'язково ЗНО з математики. У
програмі ЗНО є тема системи рівнянь. Щороку учням пропонуються
завдання з цієї теми. Тому вивчати дану тему є надзвичайно важливо.
ІІІ. Повідомлення теми та очікуваних результатів навчально – пізнавальної діяльності учнів.
Епіграф уроку: Мало знати, потрібно й використовувати.
Мало бажати, потрібно й робити.
Й. Гете
ІV. Актуалізація опорних знань.
Усне опитування «Хай живе теорія!» технологія мікрофон.
Тестові завдання на два варіанта.
V. Розв'язування систем рівнянь.
Робота в парах.
Учні розв'язують системи рівнянь методом підстановки,
додавання та графічним, потім поясняють рішення біля дошки.
Колективне розв'язування системи рівнянь з параметром.(Завдання з ЗНО).
VІ. Історична довідка. Презентація.
VІІ. Різнорівнева самостійна робота.
VІІІ. Підсумок уроку. Робота в парах. Відгадування кросворду.
ІX. Рефлексія.
Зверніть увагу на малюнок намальований на дошці. На початку уроку всі
були на першій сходинці, а зараз кожен для себе визначить на якій
сходинці він зараз.
X. Домашнє завдання
про публікацію авторської розробки
Додати розробку