Побудова геометричної моделі задач з параметрами в координатній площині (x;y).

Побудова геометричної моделі задач з параметрами в координатній площині (x;y).

 В залежності від ролі, яка відводиться параметру в задачі (нерівноправне і рівноправне з змінною) виділяють два основних графічних способи:

1. побудова графічної моделі в координатній площині XOY;
2. побудова графічної моделі в координатній площині XOA.

Розглянемо схематичну структуру першого графічного способу.

На площині XOY функція y=f(x;a) буде задавати сімейство кривих, які залежатимуть від параметра а. Від однієї кривої цього сімейства можна перейти до іншої за допомогою перетворень. Виконуючи відповідні перетворення будемо читати з графіка відповідь до задачі.

Розглянемо конкретні завдання:

Завдання 1. Знайти всі значення параметра а, при яких рівняння
tg(2 ·ǀxǀ) + lg(2-x) – lg(lg a) = 0 має єдиний корінь.

Розв’язування. Для розв’язування введемо заміну lg a = t, t>0 і використовуючи властивості логарифмів lg (2 ·ǀxǀ · (2-x)) = lg t.

Рівняння замінимо рівносильною системою.

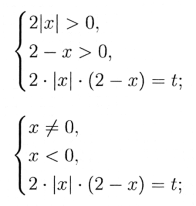
Будуємо схематичний графік функції y=2ǀxǀ · (2-x) і сімейство прямих y=t, паралельних осі OX (мал.. 2.1.)

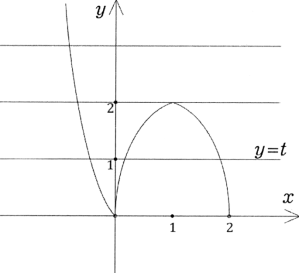
     Мал. 2.1.

 Отриманий графік сімейство прямих y=t повинен перетнути в одній точці. Отже, t>2, lg a>2. Звідси a>100.

 Відповідь. a>100.

Завдання 2. Для кожного значення параметра a знайти всі значення x, які задовольняють рівняння ǀх + 3ǀ – аǀ х – 1ǀ = 4.

Розв’язування. Запишемо рівняння у вигляді ǀх + 3ǀ – 4 = а ǀх – 1ǀ
і побудуємо схематично графік функції y = ǀх + 3ǀ – 4 (мал. 2.2.)

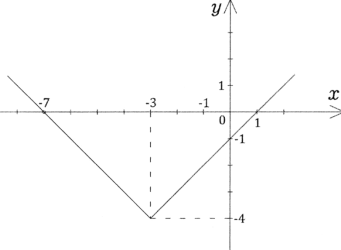
     Мал. 2.2.

Графік функції g(х) = а ǀх – 1ǀ є сімейством двох променів (при а ≠ 0) з спільною точкою (1;0), які отримуються з стисненням до осі OY (a>1) розтягом (при 0 < a < 1), і відображенням відносно осі OX при a<0 (мал. 2.3.)

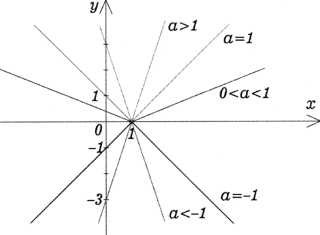
     Мал. 2.3.

Сумістивши графіки в одній системі координат отримаємо відповідь:

1. якщо а=0, то х=1 або х= -7;
2. якщо а=1, то х Є [1;+∞) – розв’язок;
3. якщо а=-1, то х Є [-3;1] – розв’язок;
4. якщо а>1, то х=1;
5. якщо а<-1, то х=1;
6. якщо 0 < a < 1 U -1 < a < 0, то х=1 або х= .

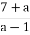Завдання 3. При яких значеннях параметру а система

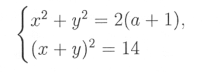
має рівно два розв’язки?

Розв’язування. Графіком другого рівняння системи є дві паралельні прямі
x + y = і x + y = - (мал.2.4.)

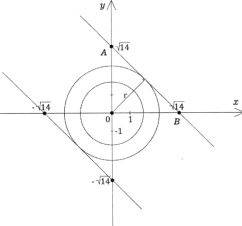 Графіком рівняння x² + y² = 2(a+1) є сімейство кіл з центром в точці О (0;0) і
радіусом r = , якщо а > -1.

 Система буде мати рівно два розв’язки, якщо одне з кіл буде дотикатися до прямих, тобто r = ·AB = .

Мал. 2.4.

Звідси = ;

2(а+1) = 7;

а+1 = ; а =

Відповідь: при а = 2,5.

Завдання 4. При яких значеннях параметра а система

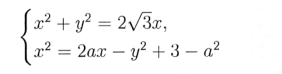
має єдиний розв’язок?

Розв’язування. Використавши спосіб групування і формулу скороченого множення перше рівняння системи запишемо

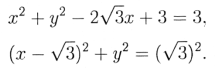
Графіком рівняння є коло з центром в точці А ( ;0) і радіусом r = .

Друге рівняння системи запишемо

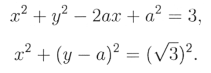
Це рівняння задає сімейство кіл з центром в точці B (0;а) і радіусом R = .

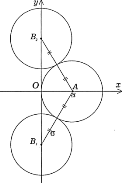Щоб виконувалась умова задачі потрібно, щоб кола розташувались як показано на мал. 2.5.

 Із трикутників В₂ОА (або В₁ОА) маємо:

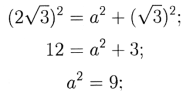В₂А² = В₂О² + ОА² (або В₁А² = В₁О² + ОА²);

    Мал. 2.5.

а = 3 або а = -3.

Відповідь: а = 3 і а = -3.

Розглянемо завдання в якому будемо розглядати не одне сімейство графіків, а два.

Завдання 5. При яких значеннях параметра а корені рівняння
ǀх – а²ǀ = а² – 4а – 5 мають однакові знаки?

Розв’язування. Перше сімейство графіків задається формулою

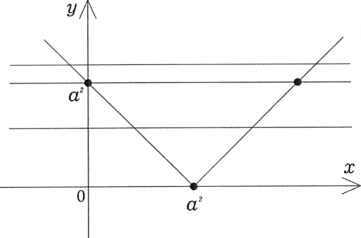
y = ǀх – а²ǀ у вигляді двох променів з початком в точці (а²;0) і кут утворений цими променями дорівнює 45^о (графіки y = ǀх – а²ǀ отримані із графіка y = ǀхǀ зсувом по осі ОХ на а² одиниць).

Мал. 2.6.

 Друге сімейство – сімейство прямих у = а² – 4а – 5 паралельних осі абсцис. Ці прямі повинні пересікати промені в точках, абсциси яких мають однакові знаки.

 З малюнку 2.6. отримуємо

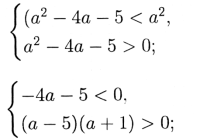
Мал. 2.7.

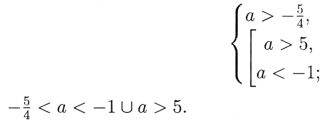
Відповідь: при – < a < – 1, а > 5.