Презентація до теми "Прогресії"

Арифметическая и геометрическая прогрессия в окружающем нас мире.

Progressia – движение вперёд

-2; 0;2; 4;… 1; 1; 2; 3; 5; 8;… -3; 3; -4; 4; -5; 5;… -4; -8; -16;… 7; 14;28;56;… -10; -8; -4;… 8; 6; 4;… 9;6;3;…

Арифметическая последовательность Геометрическая последовательность Числовая последовательность -2; 0;2; … -4; -8; -16;… 3; 3; -4; 4; -5; 5;… 8; 6; 4;… 7; 14;28;… -10; -8; -4;… 9;6; 3;… 1; 1; 2; 3; 5; 8;…

Прогрессии мы с вами изучали, И много новых формул вы узнали, Различные задачи прорешали, И вот теперь настал тот час, И вы конечно же должны узнать А применимы ли прогрессии СЕЙЧАС?

Наука достигает совершенства лишь тогда, когда ей удается пользоваться математикой. (Фридрих Энгельс)

Действительно ли прогрессии играют большую роль в повседневной жизни?

Кафедра Зав. кафедрой Финансы и кредиты Панасенко К. Физика Шпигарев В. Социология Примак А. Экономика и менеджмент Терентьева С. История науки Чичкань К.

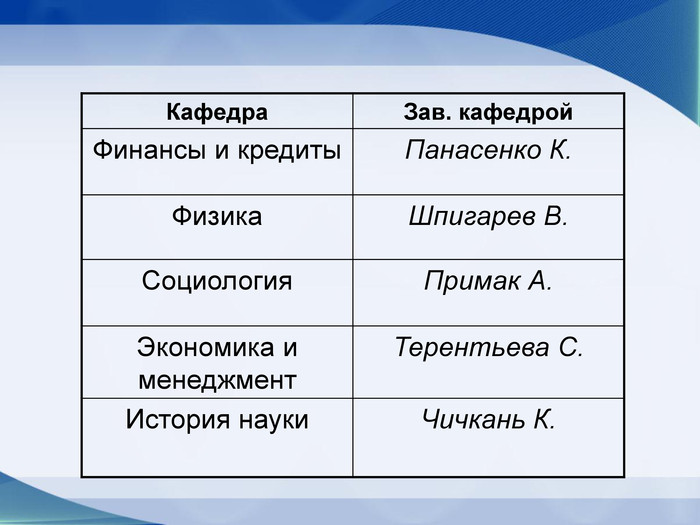
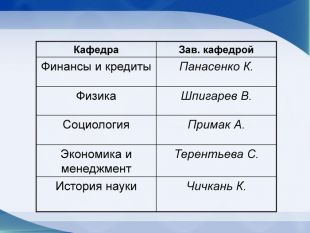
Кафедра истории науки Задача 1 Из старинного учебника математики, носящего пространное заглавие: «Полный курс чистой математики, сочиненный Артиллерии Штык-Юнкером и Математики партикулярным Учителем Ефимом Войтяховским в пользу и употребление юношества и упражняющихся в Математике» (1795г) следующая задачка: «Служившему воину дано вознаграждение за первую рану 1 копейка, за другую – 2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось, что воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран».

Задача 2. Древнейшая задача на прогрессии – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце пошлого столетия, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических и геометрических задач этого документа имеется такая: Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, насколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, два первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Кафедра финансы и кредиты 1) Банк начисляет 10% от суммы, если внесенная сумма 10000 гривен. Какая сумма будет на счету клиента банка через 5 лет? 2) Банк начисляет 20% годовых, если внесенная сумма 10000 гривен. Какая сумма будет на счету клиента банка через 5 лет?

Кафедра физики 1) Период полураспада элемента равен 2 суток. Сколько процентов радиоактивного вещества останется по истечении 6 суток? 2) Автомобиль, двигаясь со скоростью 1м/с за каждую последующую секунду изменял свою скорость на 0,6 м/с. Какую скорость он будет иметь спустя 10 секунд?

3) Чему равно перемещение свободно падающего тела в n-ю секунду после начала движения?

Кафедра социологии На сколько процентов увеличится население острова за 10 лет, если ежегодно оно увеличивается на 3%?

Кафедра менеджмента Задача 1. В старинной арифметике Л.Ф. Магницкого имеется следующая задача: Некто продал лошадь за 156 руб. Но покупатель, приобретя лошадь, раздумал ее покупать и возвратил продавцу, говоря: Нет мне расчета покупать за эту цену лошадь, которая таких денег не стоит. Тогда продавец предложил другие условия: Если, по-твоему, цена лошади высока, то купи только ее подковные гвозди, лошадь же получишь тогда впридачу бесплатно. Гвоздей в каждой подкове 6. за первый гвоздь дай мне всего ј коп., за второй – Ѕ коп., за третий – 1 коп., и т.д. Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условия продавца рассчитывая, что за гвозди придется уплатить не более 10 рублей. На сколько покупатель проторговался?

Объявление Велосипед за 100 гривен! Каждый может приобрести в собственность велосипед всего за 100 грн. Вместо 500 грн. Условия покупки высылаются бесплатно (Условие: за 100 грн. высылается 4 билета, которые надо сбыть по 100 грн. своим знакомым, собранные таким способом 400 грн. следует отправить фирме, после чего высылается велосипед). Выгодна ли фирма горожанам?

Действительно ли прогрессии играют большую роль в повседневной жизни?

Числа Фибоначчи — элементы числовой последовательности: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… в которой каждое последующее число равно сумме двух предыдущих чисел.

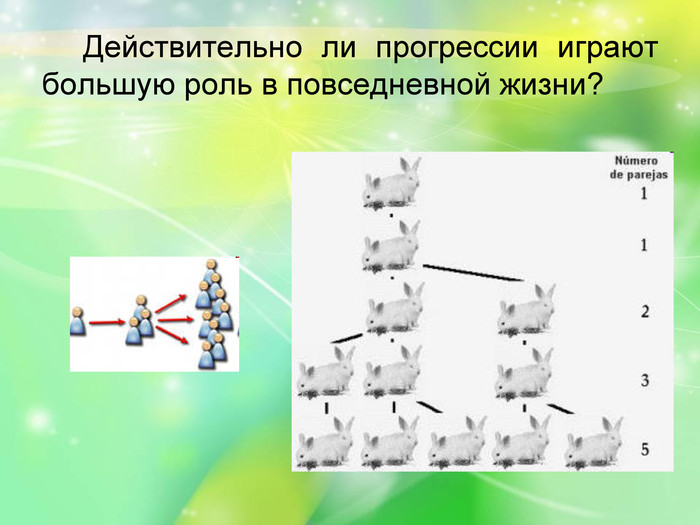
Числа Фибоначчи были известны в Индии в трудах математиков VIII—XII веков и применялись там в стихосложении. В Западной Европе последовательность введена в 1202 году в «Книге счёта» Леонардо Пизанского (Фибоначчи), где он предлагает задачу о размножении кроликов: имеется одна новорожденная пара кроликов, которая начинает давать приплод в одну пару кроликов в каждый месяц, начиная со второго месяца. Так же размножаются и вновь родившиеся кролики, порождая новую пару кроликов каждый месяц, начиная со второго, с момента своего рождения. В задаче Фибоначчи спрашивалось, сколько пар кроликов будет к концу года (считается, что кролики не умирают). В конце года будет F13=233 пары кроликов. Как это посчитать?

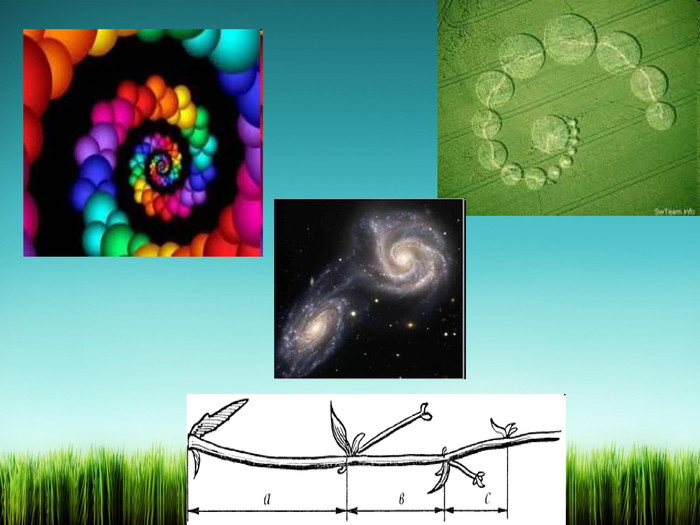
Листья, сидящие на ветке одиноко, располагаются кругом стебля, по винтовой линии, то есть каждый последующий лист повыше и в сторону от предыдущего. При этом для каждого вида растений характерен свой угол расхождения двух соседних листьев, который выдерживается более или менее точно во всех частях стебля. Числа Фибоначчи исчисляют спирали семечек в подсолнухе, спирально завитой раковине и т.п.

Вами доказано: прогрессии имеют назначение. Но разве только этим Душа науки бредит? Лирика для Физика была нужна всегда. Поэзия, что муза, ему приносит вдохновение. А в ней есть ли прогрессия? Скажите нет, иль Да!!!

Прогрессии в литературе: строки из “Евгения Онегина”. «…Не мог он ямба от хорея Как мы не бились отличить…». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха. Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2. Хорей – это стихотворный размер с ударением на нечетные слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;.. Примеры. Ямб. «Мой дЯдя сАмых чЕстных прАвил…», прогрессия 2; 4; 6; 8;… Хорей. «Я пропАл, как звЕрь в загОне»Б.Л.Пастернак, «БУря  мглОю  нЕбо  крОет» А.С. Пушкин, прогрессия 1; 3; 5;7

Мало того, великие люди даже в стихи писали в рамках «Золотой пропорции». Например, проведенный Н. Васютинским анализ стихотворений А.С. Пушкина с этой точки зрения показал, что размеры стихов распределены весьма неравномерно; оказалось, что Пушкин явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи). Многими исследователями было замечено, что стихотворения подобны музыкальным произведениям; в них также существуют кульминационные пункты, которые делят стихотворение в пропорции золотого сечения. Рассмотрим, например, стихотворение А.С. Пушкина «Сапожник»: Картину раз высматривал сапожник И в обуви ошибку указал; Взяв тотчас кисть, исправился художник, Вот, подбочась, сапожник продолжал: «Мне кажется, лицо немного криво… А эта грудь не слишком ли нага? Тут Апеллес прервал нетерпеливо: «Суди, дружок, не выше сапога!"

Есть у меня приятель на примете: Не ведаю, в каком бы он предмете Был знатоком, хоть строг он на словах, Но черт его несет судить о свете: Попробуй он судить о сапогах! Проведем анализ этой притчи. Стихотворение состоит из 13 строк. В нем выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 — числа Фибоначчи). Совпадение, или автор надумал что то? Разбираем дальше великого поэта… Кульминацией главы является объяснение Евгения в любви к Татьяне — строка "Бледнеть и гаснуть… вот блаженство!". Эта строка делит всю восьмую главу на две части — в первой 477 строк, а во второй — 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!.. Вполне вероятно что Пушкин даже никогда не слышал о Фибоначчи и Золотой пропорции, но творил он свои произведения подчиняясь именно ей. Точно такую же закономерность можно проследить и в классической музыке, и найти золотую пропорцию в шедеврах Баха, Бетховена, Шопена, Вагнера. Например, исследуя Хроматическую фантазию и фугу Баха, за единицу меры во времени была принята длительность четверти. В этом произведении содержится 330 таких единиц меры. Золотое деление этого интервала приходится на 204-ю четверть от начала. Этот момент золотого сечения точно совпадает с ферматой (в нотной грамоте знак ферматы увеличивает длительность звука или паузы обычно в 1,5-2 раза), которая отделяет первую часть произведения (прелюдию) от второй. Поразительную соразмерность частей демонстрирует также фуга, следующая за фантазией. При взгляде на схему гармоничного анализа фуги «невольно приходишь в священный трепет перед гениальностью мастера, воплотившего силою художественной чуткости до такой степени точности сокровенные законы природного творчества