Конспект учня на час карантину з теми :"Зведення подібних доданків"

13.03

Класна робота

Властивості множення раціональних виразів. Коефіціент буквенного виразу. Зведення подібних доданків

[усно]

Для множення раціональних чисел, як і для множення додатних чисел, справджуються переставна і сполучна властивості.

Переставна властивість множення.

– Для будь-яких раціональних чисел а і b виконується рівність ab = ba.

Приклад:

 -3 ∙ 2 = -6   або 2 ∙ (-3) = -6, тому -3 ∙ 2 = = 2 ∙ (-3)

Сполучна властивість множення.

Для будь-яких раціональних чисел а, b і c виконується рівність (ab)c = a(bc).

Приклад.

(-2 ∙ 3) ∙ (-4) = -6 ∙ (-4) = 24    або   -2 ∙ (3 ∙ (-4)) = = -2 ∙ (-12) = 24, тому (-2 ∙ 3) ∙ (-4) = -2 ∙ (3 -4)).

Властивості множення дають можливість спростити процес обчислення добутку кількох множників, обираючи зручний порядок обчислень.

-25 -4) (-1 ) = (-25 -4)) ((-1 ) ) = 100 (-1) = -100.

Добуток дорівнює нулю, якщо хоча б один із множників дорівнює нулю.

-25 -4) (-1 )

Розподільна властивість множення.

Для будь-яких раціональних чисел а, Ь і с справджується рівність: (а + b)с = ас + bс.

Приклад :

Нехай а =-4; 6 = 7; с = -5:

(-4 + 7) • (-5) = 3 • (-5) = -15 або

 -4 • (-5) + 7 • (-5) = 20 + (-35) = -15.

Отже, (-4 + 7) • (-5) = -4 • (-5) + 7 • (-5).

Заміну виразу (а + Ь)с на вираз ас + Ьс називають розкриттям дужок, а навпаки – винесення спільного множника за дужки.

[письмово]

Числовим виразом називається запис, складений із чисел, знаків арифметичних дій і дужок. 

2+(-3),    33-14(-5) і т.д

Буквеним виразом називається запис, складений із букв, чисел, знаків арифметичних дій і дужок.

3a+x, 2y+12 і т.д

Приклад1. Спростити вираз -2а ∙ 3b ∙ (-5)

Розв’язання. -2а ∙ 3b ∙ (-5) = -2 ∙ а ∙ 3 ∙ b ∙ (-5) = (-2 ∙ 3 ∙ (-5)) ∙ (а ∙ b) = 30аb

 30 аb.

Доданки, що мають однакову буквену частину, називають подібними доданками.

Додавання подібних доданків називають зведенням подібних доданків.

Щоб звести подібні доданки, достатньо додати їх коефіцієнти і знайдений результат помножити на спільну буквену частину.

Вправи1

Звести подібні доданки: 1) 4а + а – 6а; 2) 7b – 3b – 4b.

1. У цьому прикладі всі доданки подібні, оскільки в них спільна частина а. Додаючи коефіцієнти, маємо: 4 + 1 – 6 = -1.

Отже, 4а + а – 6а = -1 ∙ а = – а;

2. Самостійно!(д.з)

Вираз може містити доданки з різними буквеними частинами. Тоді доданки можна об’єднати у групи з однаковою буквеною частиною. Доданки з різних груп доцільно підкреслювати по-різному.

Вправи2 Спростити вираз  1. 4а + 5b – 7а + 4 + 3b., 2. 3а – 8а +5х – 1 – 3х.

1. 
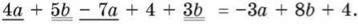
2. Самостійно!(д.з)

Вправа 3. Розв’язати рівняння 1) 4(x + 2) – (x – 2) = 13. 2) х-4 – (2х+4)=8

Розв’язання.

1. Розкриємо дужки (переставний закон): 4x + 8 – x + 2 = 13.
2. Зведемо подібні доданки 3x + 10 = 13.
3. 3x = 13 – 10;

3x = 3;

x = 3 : 3;

 x = 1.

3. Самостійно! (д.з)

Вправа 4.

Розкрий дужки і зведи подібні доданки:

1) 2(3x – 5) + 4x; 2) – ( 7a + 8) + 3a;

3) 7x + (x – 3); 4) 2у – 3(у – 5)

1. = 6х – 10+4х = 10х-10.

2. Самостійно (д.з)

3. Самостійно (д.з)

4. = 2у – 3у + 15 = -у + 15 (Одиницю перед літерою не пишемо)

Вправа 5. Спрости вираз та знайди його значення:

1) – (2m – 0,2) + 2(4m – 0,1), якщо m = 0,7;

2) 3(2x – 0,8) – (6x + 0,4), якщо x = 1,83

1. Розкриємо дужки = -2m + 0,2 + 8m – 0,2 = 6m + 0 = 6m.

2. Самостійно (д.з)