Конспект уроку " Квадратні нерівності"

Тема уроку. Квадратичні нерівності.

Мета: Сформувати поняття квадратичної нерівності, вміння за допомогою графіка квадратичної функції розв’язувати квадратні нерівності. Формування складати план до вивчення нової теми та діяти за ним.

Тип уроку: засвоєння нових знань та вмінь.

Хід уроку.

1. Організаційний момент.
2. Перевірка домашнього завдання.
3. Актуалізація опорних знань.

Математичний диктант:

1. Якщо а-в є додатнім числом, тоді а відносно в буде ( більшим).
2. Якщо а-в є від’ємним числом, тоді а відносно в буде (меншим).
3. Значення змінної нерівності, яке перетворює її в правильну числову нерівність називається ( розв’язком).
4. Сукупність розв’язків нерівності утворюють ( множину).
5. Якщо нерівність не має розв’язків, то говорять, що її множина розв’язків буде (порожня).
6. Два проміжки, які є розв’язком однієї нерівності утворюють (об’єднання).
7. Спільні розв’язки з двох проміжків утворюють (перетин ).
8. Функція виду ах²+вх+с=у, де а, в,с – де-які числа, х – аргумент, називається (квадратичною).
9. Проміжок, на якому функція набуває значень однакового знака, називають проміжком (знакосталості).
10. Графіком квадратичної функції є (парабола).
11.  Напрям вітей параболи залежить від (головного коефіцієнта ).
12.  Кількість точек перетину параболи з віссю Ох залежить від (дискримінанта ).

( діти обмінюються зошитами та здійснюють перевірку, вчитель називає правильні відповіді ).

4. Вивчення нового матеріалу.

1. Означення квадратичної функції.

Побудуємо графік функції  y=x²−2x−3  і розглянемо його:

• Визначимо напрямок віток параболи. У рівнянні даної функції  a >0,  отже вітки її графіка напрямлені вгору.
• Визначимо координати вершини параболи:
  (1;−4)(1;−4). Позначимо її на координатній площині, і проведемо пряму x=1
• найдемо абсциси точок перетину графіка з віссю Ox x²−2x−3=0. За теоремою, оберненою до теореми Вієта, маємо: x₁=−1, x₂=3.
  Отже, точки перетину параболи з віссю Ox мають координати (−1;0) і (3;0). Відкладемо їх.
• Візьмемо ще пару точок. Побудємо для цього таблицю значень:

і відкладемо точки із зазаначеними у таблиці координатами:

•  Всі знайдені точки сполучаємо  плавною лінією.

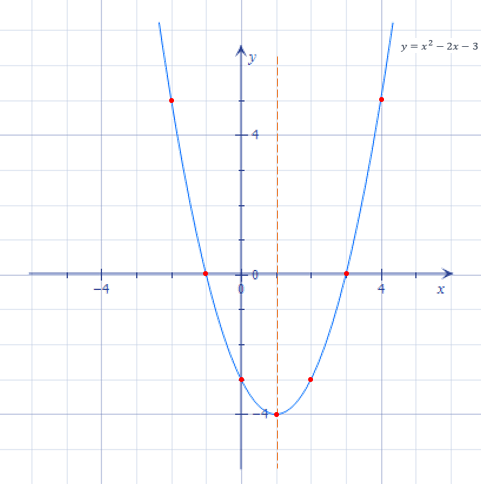
Слова вчителя. Розглянемо уважніше отриманий графік. Як бачимо, віссю Ох він ділиться на дві частини. Скажіть мені будь ласка:

- Що можна сказати про частину графіка функції, яка    знаходиться над віссю Ох?( у всіх точках графіка функція набуває додатніх значень, тобто у > 0)

-Що можна сказати про частину графіка, що знаходиться під віссю Ох? ?( у всіх точках графіка функція набуває від’ємних значень, тобто у ˂ 0)

- Запишемо проміжки на яких функція набуває додатніх значень:

 хϵ( -∞; -1)U( 3; +∞)

-Запишемо проміжки на яких функція набуває від’ємних значень:

хϵ( -1; 3)

-Як ці проміжки називаються? ( проміжки знакосталості)

-Яке має значення проміжок знакосталості для нашої фукції?

Запишемо:

якщо хϵ( -∞; -1)U( 3; +∞) , тоді у = x²−2x−3> 0;

якщо  хϵ( -1; 3), тоді у = x²−2x−3˂ 0.

Таким чином, ми отримали розв’язання двох нерівностей.

Запишемо в загальному вигляді ці нерівності:

ах²+вх+с > 0 та ах²+вх+с ˂ 0,

де а, в, с – деякі числа, х – змінна ,  а ≠ 0

-Як можна назвати ці нерівності, враховуючи, що ліва частина є квадратний тричлен ? ( Квдратними нерівностями )

5. Засвоєння нових знань і створення плану розв’язання квадратних нерівностей.

1. За допомогою графіка розв’язати квадратну нерівність:                 -х²- 6х - 5>0.
2. Звернути увагу дітей на те, що розв’язання квадратних нерівностей залежить від:

• напряму вітей параболи ;
• точок перетину з віссю Ох.

3. Створити план розв’язання квадратних нерівностей на прикладі х² + 6х – 7 ˂ 0.

6. Закріплення набутих знань.

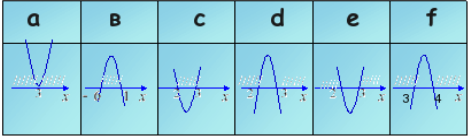
1. Виберіть з таблиці графічну інтерпретацію для кожної нерівності:  - х² – 5х +6 > 0

                    х² – 5х + 6 ˂ 0

                  -х² + 7х – 12 ˂ 0

                   х² – 6х + 9 > 0

2. Виконати вправи за підручником: № 12.18; 12.21.

7. Домашне завдання : вивчити означення квадратної нарівності за підручником, за створеним планом розв’язання квадратних нерівностей виконати вправу 12.17 ( 1 – 5).