Конспект уроку на тему "Нерівність трикутника"

          Богдан Юлія

Урок №35        Дата ___________

Тема: Нерівність трикутника.

Мета:

навчити домогтися засвоєння змісту теореми, що виражає нерівність трикутника, і наслідок з неї; навчитися застосовувати теорему й наслідок під час розв'язування задач;

розвинути логіко-дидактичне мислення , вміння аналізувати, узагальнювати, виконувати дії за аналогією;

виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу як індивідуальну так і групову (формування соціальної компетентності).

Обладнання: Підручник з математики 7 клас (Істер), Збірник задач і контрольних робіт з алгебри 7 клас (Мерзляк).

Хід уроку

1. Організаційний етап

• Привітання
• Перевірка присутності учнів на уроці
• Перевірка готовності учнів та кабінету до уроку

2. Перевірка домашнього завдання

Чи були у вас проблеми при виконанні завдань? Якщо так, то один з учнів хто виконав це завдання пояснює його біля дошки. Якщо ні, то просто перевіряю наявність домашньої роботи у зошитах.

3. Формулювання мети й завдань уроку, мотивація навчальної діяльності

Трикутник – ключова фігура планіметрії. Існує багато різних видів трикутників, проте всім їм притаманні деякі спільні властивості. На попередньому уроці ми розглянули одну з них, а сьогодні вивчимо ще одну.

4. Актуалізація опорних знань

1. Що таке трикутник?
2. З яких елементів складається трикутник?
3. Намалюйте трикутник ABC та вкажіть усі його елементи.
4. Що ми знаємо про кути трикутника?
5. Електронний тест https://learningapps.org/3424219

5. Засвоєння нових знань

Розглянемо 5 різних трикутників запишеио у таблицю довжини їх сторін та суми

Розглянувши таблицю бачимо, що сума 2 сторін завжди більша за третю.

Т. (нерівність трикутника) Кожна сторона трикутника менша від суми двох інших його сторін.

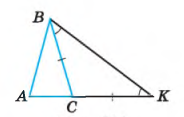
□ розглянемо довільний трикутник ABC і доведемо, що його сторона наприклад АВ, менша від суми двох інших сторін АС і СВ.

1) відкладемо на продовжені сторони АС відрізок СК, що дорівнює стороні ВС. Тоді ВСК – рівнобедрений і тому СВК=СКВ.

2) АВК>СВК, тому АВК>АКВ. Оскільки в трикутнику проти більшого кута лежить більша сторона, то АВ<AК. Але ж АК=АС+СК=АС+ВС. Отже, АВ<AC+BC.

Аналогічно можна довести, що АС<AB+BC, BC<AB+AC. ■

Наслідок. Кожна зі сторін трикутника більша за різницю двох інших його сторін.

□ Запишемо нерівність трикутника для трикутника АВС: АВ < АС + ВС. Віднявши від обох її частин, наприклад АС, матимемо: АВ-АС < ВС. (Таку дію можна виконати, використовуючи властивості нерівностей, які розглядатимуться в курсі алгебри). Отже, ВС > АВ - АС. Аналогічно: АС>ВС-
-АВ, АВ > ВС - АС. ■

Оскільки, наприклад, ВС>АВ-АС і ВС>АС-АВ, то, узагальнюючи, отримаємо ВС > |АВ – АС|. З теореми про нерівність трикутника та наслідку з неї отримаємо важливе співвідношення між сторонами трикутника: кожна сторона трикутника менша від суми двох інших сторін, але більша за модуль їх різниці. Наприклад, |АВ – АС|< ВС < АВ + АС.

Приклад 1. Чи існує трикутник зі сторонами 5 см, 9 см, 13 см?

13<5+9
5+9=14
13<14

Такий трикутник існує.

Методичний коментар. Для того щоб дати відповідь на запитання задачі слід утворити та перевірити нерівність трикутника для найдовшої сторони. Знайти суму інших двох та порівняти із довжиною третьої сторони.

Приклад 2. Чи існує трикутник зі сторонами 5 см, 9 см, 15 см?

153<5+9
5+9=14
14<15

Такий трикутник не існує.

Методичний коментар. Для того щоб дати відповідь на запитання задачі слід утворити та перевірити нерівність трикутника для найдовшої сторони. Знайти суму інших двох та порівняти із довжиною третьої сторони.

Приклад 3. Знайдіть сторону АС рівнобедреного трикутника АВС якщо АВ=10см, ВС=4 см.

Припустимо, що рівними є сторони довжина яких 4 см. Складемо нерівність трикутника

10<4+4
10<8

Нерівність Не вірна. Отже припущення було не вірним.

Припустимо, що рівними є сторони довжина яких 10 см. Складемо нерівність трикутника

10<4+10
10<14

Нерівність вірна, отже третя сторона трикутника = 10 см.

Приклад 4. У трикутнику АВС відомо, що АВ=1,2 см, АС=2,3 см. Знайдіть третю сторону цього трикутника, якщо її довжина, виражена в сантиметрах, дорівнює цілому числу. Скільки розв'язків має задача?

Позначимо третю сторону через Х.

Утворимо 3 нерівності трикутника:

х<1,2+2,3
1,2<x+2,3
2,3<x+1,2

З першої нерівності маємо х<3,5, так як довжина шуканої сторони ціле число, то можливими розв'язками є: х=1, х=2, х=3.

Перевіримо чи задовільняють знайдені значення 2 нерівність:

1,2<1+2,3
1,2<2+2,3
1,2<3+2,3

Перевіримо чи задовільняють знайдені значення 3 нерівність:

2,3<1+1,2 – нерівність

2,3<2+1,2
2,3<3+2,3

Отже дана задача маж 2 розв'язки: 2 та 3.

6. Вправи для закріплення

Індивідуальна робота біля дошки. Учні по черзі виходять до дошки та виконують з детальним коментуванням запропоновані завдання. (К. – володіння державною та рідною мовою)

№ 496 (Істер)

1. 7<5+2
   7<7
   Нерівність не вірна, отже такого трикутника НЕ існує.
2. 6<2+3
   6<5
   Нерівність не вірна, отже такого трикутника НЕ існує.
3. 5<2+4
   5<6
   Нерівність вірна, отже такий трикутника існує.

Методичний коментар: для того щоб дати відповідь на запитання задачі слід утворити нерівність трикутника для найдовшої сторони, оцінити отриману нерівність та оцінити результат.

№ 498 (Істер)

Нехай третя сторона = х см.

Утворимо 3 нерівності трикутника:

х<2,9+4,5
2,9<x+4,5
4,5<x+2,9.

З першої нерівності маємо х<7,4, так як довжина шуканої сторони ціле число, то можливими розв'язками є: х=1, 2, 3, 4, 5, 6, 7.

Перевіримо чи задовільняють знайдені значення 2 нерівність:

2,9<1+4,5 - 2,9<5,5
2,9<2+4,5 - 2,9<6,5
2,9<3+4,5 - 2,9<7,5
2,9<4+4,5 - 2,9<8,5
2,9<5+4,5 - 2,9<9,5
2,9<6+4,5 - 2,9<10,5
2,9<7+4,5- 2,9<11,5
Всі нерівності вірні, томі перевіримо можливі розв’язки для 3 нерівності

4,5<1+2,9 - 4,5<3,9.

4,5<2+2,9 - 4,5<4,9.

4,5<3+2,9.

4,5<4+2,9.

4,5<5+2,9.

4,5<6+2,9.

4,5<7+2,9.

Отже найменше можливе значення довжини 3 сторони – 4 см.

Методичний коментар: для того щоб дати відповідь на запитання задачі слід позначити шукану сторону через змінну х та утворити 3 нерівності трикутника. Проаналізувавши 1 з них отримаємо усі можливі значення шуканої сторони, далі перевіримо ці значення по черзі підставляючи їх у 2 та 3 нерівності. Проаналізувавши вірність отриманих нерівностей дати відповідь на запитання задачі.

Робота в групах. Для виконання наступних завдань діти об’єднуються у 3 групи. Завдання слід виконати швидко та правильно. Після виконання завдань група вибирає 1 представника який біля дошки пояснює виконання 1 із завдань. (к. Соціальна)

№ 499 (Істер)

1.  Нехай х – коефіцієнт пропорційності, тоді сторони трикутника відповідно дорівнюють 2х, 3х, 4х.

Утворимо нерівність трикутника для найдовшої сторони

4х<2х+3х
4х<5х

Нерівність вірна, отже сторони трикутника можуть бути пропорційними числам 2, 3, 4.

2. Нехай х – коефіцієнт пропорційності, тоді сторони трикутника відповідно дорівнюють 7х, 8х, 15х.

Утворимо нерівність трикутника для найдовшої сторони

15х<7х+8х
15х<15х

Нерівність НЕ вірна, отже сторони трикутника НЕ можуть бути пропорційними числам 7, 8, 15.

3. Нехай х – коефіцієнт пропорційності, тоді сторони трикутника відповідно дорівнюють 5х, 3х, 7х.

Утворимо нерівність трикутника для найдовшої сторони

7х<5х+3х
7х<8х

Нерівність вірна, отже сторони трикутника можуть бути пропорційними числам 5, 3, 7.

Методичний коментар: для того щоб дати відповідь на запитання задачі слід ввести коефіцієнт пропорційності, скласти нерівність трикутника для найдовшої сторони, проаналізувати її та зробити висновок.

№ 501 (Істер)

Якщо бічна сторона трикутника = 3 см, то ще одна його сторона = 3 см. На третю сторону залишається 12-(3+3)=6 см. Складемо нерівність трикутника для найдовшої сторони

6<3+3
6<6

Нерівність Не вірна, отже такого рівнобедреного трикутника Не існує.

Методичний коментар: для того дати відповідь на запитання задачі слід знайти усі 3 сторони трикутника, для цього потрібно застосувати знання про рівнобедрений трикутник та периметр трикутника. Потім слід записати нерівність трикутника для найбільшої сторони, проаналізувати її та зробити висновок.

7. Підбиття підсумків уроку

• Тест «Нерівність трикутника»
• Що нового ви дізналися сьогодні на уроці?
• Що було для вас уже відомим?
• Що було цікавим на уроці?
• Тест для перевірки якості засвоєння матеріалу

https://learningapps.org/4748513

8. Домашнє завдання

§ 20 № 495, 499.