Урок "Функція y=tgx, її графік та властивості"
З ДОСВІДУ РОБОТИ
КОНСПЕКТ УРОКУ ПО ТЕМІ:
« Функція y = tg x:
графік та властивості»
алгебра і початки аналізу
10 клас
вчителя математики
СЗШ № 3 І-ІІІ ступенів І. Я. ФРАНКА
міста Стрия
ТКАЧУК-СИДОРИК
ЛЕСІ РОМАНІВНИ
СТРИЙ
2012
Тема . Функція y = tg x: графік та властивості
Мета уроку.
- Навчальна : домогтися засвоєння учнями основних понять, пов'язаних з означенням функції у = tgx, її властивостями, побудовою графіка (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакосталості; найбільші і найменші значення); вміти застосовувати властивості функції під час розв'язування вправ; повторити поведінку тригонометричних функцій на чвертях.
- Виховна - виховувати культуру мовного спілкування в ході бесіди, формувати правильну математичну мову, активну громадянську позицію, навики самостійно приймати рішення; розвивати творчий та естетичний потенціал, логічне і критичне мислення учнів; стимулювати розвиток умінь учнів аргументувати свою відповідь.
- Розвиваюча – розвивати в учнів вміння практичної реалізації системи знань в систему вмінь та предметних компетенцій, вміння реалізовувати прикладні зв’язки через систему курсу математики з фізикою, астрономією та міжрівневі зв’язки математики. Підтримувати інтерес до нових засобів навчання. Формувати навички творчого застосування знань до виконання вправ.
Методична мета уроку: реалізація інформаційно – комунікативних технологій, творчої складової в процесі формування вмінь та навичок учнів, застосування активних форм і методів виховання особистості учня.
Тип уроку: комбінований .
Форми роботи: колективна, групова, індивідуальна. Прийоми: фронтальна бесіда, тренувальні вправи, самостійна робота,
випереджувальні завдання, ілюстрації, елементи ігрових технологій.
Девіз уроку:
Перед людиною є три шляхи до пізнання: шлях мислення - найбільш
благородний, шлях наслідування - найбільш легкий і шлях особистого
досвіду - найбільш важкий. Конфуцій
Епіграф: «Випереди себе вчорашнього».
Міжпредметні зв’язки.
Забезпечуючі. Геометрія 8 клас. Розв’язування прямокутних трикутників
Геометрія 9 клас. Розв’язування трикутників
Забезпечувані. Фізика. Гармонійні коливання.
Динаміка.
Оптика
Алгебра і початки аналізу. Комплексні числа.
Диференціальне числення
Астрономія. Астрономічні дослідження
Забезпечення заняття:
-
Література:
- А.Г.Мерзляк, Д.А.Номіровський, В.Б.Полонський, М.С. Якір
Алгебра і початки аналізу. 10 клас ;
- А.Г.Мерзляк «Дидактичні матеріали. Алгебра і початки аналізу. 10 клас
- М.І. Шкіль. Алгебра і початки аналізу. 10 клас
- О.М. Роганін. Плани – конспекти уроків.
- Наочні посібники. Презентації:
- «Функція y = tg x: графік та властивості»
- «Тренувальні вправи «Перетворення графіків функцій»
- Роздатковий матеріал.
- Математичний диктант;
- Таблиця «Тригонометричні функції числового аргументу»;
- Таблиця «Значення тригонометричних функцій деяких кутів»;
- «Віднови записи».
4. Технічні засоби навчання. Мультимедійний проектор.
Компетенції. Навчальна, соціально – трудова, стимулювально – мотиваційна.
Функції:
Теоретична : знати: поняття «Тригонометрична функція тангенс»
Повторити поняття: «радіанна та градусна міра кута», «одиничне коло», «тригонометричні функції числового аргументу», знаки тригонометричних функцій на чвертях, монотонність тригонометричних функцій на чвертях, співвідношення між тригонометричними функціями числового аргументу, властивості тригонометричних функцій синус і косинус.
Практична: вміти: будувати графік тригонометричної функції тангенс, описати її властивості, застосовувати їх до розв’язування вправ; застосовувати перетворення графіків функцій щодо даного графіка.
Повторити: перетворення градусної міри кута в радіанну і навпаки, відповідність між дійсними числами і точками на одиничному колі; обчислення значення тригонометричних функцій числового аргументу для окремих кутів.
ХІД УРОКУ:
- Організаційний етап. (Метод: психолого – педагогічної підтримки роботи учнів на уроці) 2 хв.
Учитель. Які асоціації викликає у вас слово «урок»?
У —успіх...
Р —радість...
О — обдарованість...
К — компетентність...
Сподіваюся, що сьогодні на нас чекає і успіх, і радість. Ви зможете продемонструвати власну обдарованість і компетентність.
-
Перевірка домашнього завдання.
- Виберіть правильну відповідь
![]()
![]()
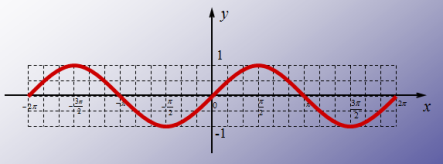 2.1.1. 1.Користуючись графіком функції, вкажіть проміжки, де функція спадає
2.1.1. 1.Користуючись графіком функції, вкажіть проміжки, де функція спадає
А) Б)
![]()
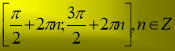
В) Г)
2.1.2

Користуючись графіком функції, вкажіть проміжки, де функція набуває додатних значень
![]() А)
А)
![]() Б)
Б)
![]()
В)
2.1.3 Користуючись графіком функції, вкажіть точки, в яких функція набуває найменшого значення
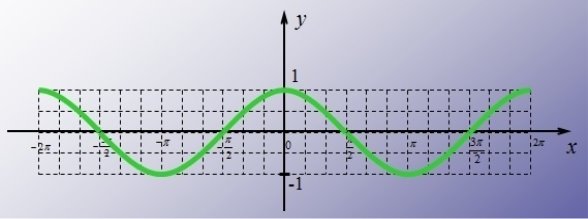

А)
![]() Б)
Б)
![]()
В)
2.2 Перевірити правильність побудови графіків функцій вправи № 2 за рисунком, зробленими до уроку.
На дошці зображено графік функції.
Дати відповіді на питання (в дужках – очікувані відповіді):
1. Графік якої функції зображено? ( у = 2sin 2x).
2. Назвати період цієї функції (Т = ![]() ).
).
3. Функція парна чи непарна? (Функція непарна).
4. Назвати область визначення і область значень цієї функції. (D(f)![]() R, Е(f)[-2;2]).
R, Е(f)[-2;2]).
5. Назвати нулі функції. (у = 0, при х = ![]() , n
, n ![]() Z).
Z).
6. Назвати проміжки знакосталості, монотонності функції.
у > 0 при ![]() n
n ![]() Z.
Z.
у зростає при ![]()
у спадає при![]() n
n ![]() Z.
Z.
3. Формулювання теми, мети і завдань уроку.
- Мотивація пізнавальної діяльності учнів.
(метод – історично – довідковий, випереджальне завдання: «Застосування відомостей про функцію у= tqх, історичні відомості»).
Епіграф: «Випереди себе вчорашнього».
Невеличкий екскурс в минуле…
Вавілоняни вже на початку III тисячоліття до н.е. мали календар з розподілом року на 12 місяців. Отже, вони вміли визначати положення сонця і зірок на небосхилі, тобто володіли певними знаннями тригонометричного характеру.
Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць – Америго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель. Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані. Це дало поштовх стрімкому розвиткові астрономії, а ця наука неможлива без тригонометрії.
Завершальний етап у розвитку тригонометрії пов'язаний з ім’ям Леонарда Ейлера. Він упорядкував питання про знаки тригонометричних функцій у різних чвертях, ввів однакове позначення сторін трикутника: а, в, с і протилежних кутів А, В, С; розробив тригонометрію як науку про тригонометричні функції, запропонував розглядати тригонометричні функції як числа, що виражають відношення відповідних тригонометричних ліній до радіуса кола.
- Прикладне спрямування теми у формуванні майбутнього компетентного фахівця. (Метод: переконання )
Тригонометрія має велике практичне значення, зокрема, для розв’язання задач на знаходження площ і об’ємів, на додавання і розкладання сил, на знаходження відстаней до недоступних предметів тощо. Вона широко застосовується в механіці, топографії, астрономії. Велике значення має тригонометрія також у навігаційній справі, бо й тут неабияку роль відіграють вимірювання на поверхні Землі. Тригонометричні обчислення застосовуються практично у всіх областях геометрії, фізики й інженерної справи. Велике значення має техніка тріангуляції, що дозволяє вимірювати відстані до недалеких зірок в астрономії, між орієнтирами в географії, контролювати системи навігації супутників. Також слід відзначити застосування тригонометрії в таких областях, як теорія музики,акустика, оптика, аналіз фінансових ринків, електроніка, статистика, біологія, медицина (включаючи ультразвукове дослідження (УЗД) і комп'ютерну томографію), фармацевтика, теорія ймовірностей, хімія, теорія чисел, криптографія, сейсмологія, метеорологія, океанологія, картографія, фізика, топографія та геодезія, архітектура, фонетика, економіка, електронна техніка, машинобудування, комп'ютерна графіка, кристалографія.
|
|
- Актуалізація опорних знань учнів.
4.1 Математичний диктант
- Тригонометрія ґрунтується на … (співвідношенні подібності).
- Відношення довжин сторін у подібних трикутників однакове, тому відношення сторін прямокутних трикутників залежить тільки від одного параметра - … ( гострого кута).
- Спочатку тригонометричні функції були пов'язані з співвідношеннями сторін у прямокутному трикутнику. Їхнім єдиним аргументом є кут (один з гострих кутів цього трикутника), тому … (тангенс) - відношення протилежного катета до прилеглого.
-
Дані визначення дозволяють обчислити значення функцій для гострих кутів, тобто від 0 до 90 (від 0 до
 радіан). У XVIII столітті Леонард Ейлер дав сучасні, більш загальні визначення, розширивши область визначення цих функцій на всю числову вісь. Тангенсом кута повороту ɑ називають … (відношення синуса цього кута до його косинуса).
радіан). У XVIII столітті Леонард Ейлер дав сучасні, більш загальні визначення, розширивши область визначення цих функцій на всю числову вісь. Тангенсом кута повороту ɑ називають … (відношення синуса цього кута до його косинуса).
- Пряму паралельну осі ОУ, що проходить через точку з координатами (1;0) називають … (віссю тангенсів).
- Вираз tqx має смисл при будь-якому х, крім чисел виду …
х =![]()
- Оскільки tqɑ - це ордината точки Тɑ лінії тангенсів, то областю значень тангенса є … (R).
- Оскільки точки Тɑ і Т-ɑ симетричні відносно Ро лінії тангенсів, то …
( tq(-ɑ) = - tqɑ).
- При зміні кута від - π/2 до π/2 ордината точки То лінії тангенсів збільшується від -∞ до + ∞, тобто tqɑ … (зростає) на проміжку (-π/2;π/2).
- Найменший додатній період тангенса дорівнює … ( π).
Математичний диктант
|
1 |
|||
|
Перед твариною |
Перед людиною |
Перед учнем |
|
|
2 |
прямого кута |
гострого кута |
тупого кута |
|
є один шлях- |
є три шляхи - |
є безліч шляхів- |
|
|
3 |
котангенс |
синус |
|
|
до науки: |
до роботи: |
до пізнання: |
|
|
4 |
відношення синуса цього кута до його косинуса |
відношення косинуса цього кута до його синуса |
відношення синуса цього кута до синуса другого кута |
|
шлях мислення |
шлях вивчення |
шлях повторення |
|
|
5 |
віссю котангенсів |
асимптотою |
віссю тангенсів |
|
- найбільш дорогий, |
- найбільш дешевий, |
- найбільш благородний, |
|
|
6 |
х = |
х = |
х = |
|
шлях наслідування - |
шлях предків - |
шлях вчителів - |
|
|
7 |
R |
Z |
N |
|
найбільш легкий |
найбільш приємний |
найбільш точний |
|
|
8 |
tq(-ɑ) = - tqɑ |
tq(-ɑ) = tqɑ |
tq(-ɑ) = - tq(-ɑ) |
|
і шлях особистого |
і шлях друга |
і шлях однокласника |
|
|
9 |
спадає |
зростає |
сталий |
|
навчання - |
досвіду - |
розуму - |
|
|
10 |
2π |
3π |
π |
|
найбільш зрозумілий. |
найбільш вдалий. |
найбільш важкий. |
Перед людиною є три шляхи до пізнання:
шлях мислення - найбільш благородний,
шлях наслідування - найбільш легкий
і шлях особистого досвіду – найбільш важкий.
Конфуцій
4.2. «Віднови записи»
tg 30° = ![]()
tg ![]() = 1
= 1
tg ![]() =
= ![]()
tg (-45°) = - 1
tg ![]() - не існує
- не існує
tg 60° = ![]()
tg π = 0
4.3 «Знайди помилку»
№1. Якій чверті належить Рα, якщо:
а) sin α cos α > 0;
б) tg α cos α > 0;
в) ctg α sin α < 0?
Відповіді:
- І
- І
- ІІІ
Очікувана відповідь: а) І або III; 6) І або II; в) II або III.
№2. Порівняти з нулем:
а) tg 2 · tg 3 · ctg 3 · cos 1;
б) sin 1 · cos 2 · tg 3 · ctg 4;
в) tg 1 · cos 3 · сtg 2 · tg 2.
Відповіді:
- ≥ 0;
- ≤ 0;
- ≤ 0.
Очікувана відповідь: а) < 0; б) > 0; в) < 0.
-
 Вивчення нового матеріалу: властивостей тригонометричної функції у = tgx; побудова графіка
Вивчення нового матеріалу: властивостей тригонометричної функції у = tgx; побудова графіка
ПЛАН
- Означення функції у = tgx.
- Область визначення функції у = tgx.
- Область значень функції у = tgx.
- Графік функції у = tgx.
- Властивості функції у = tgx.
- Перетворення графіка функції у = tgx.
 Тангенсом числа α називається відношення синуса числа α до його косинуса:
Тангенсом числа α називається відношення синуса числа α до його косинуса: ![]() .
.
Тангенс визначений для всіх а, крім тих значень, для яких cos α = 0, тобто для α = ![]() + πn, n
+ πn, n ![]() Ζ.
Ζ.
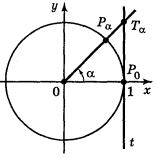
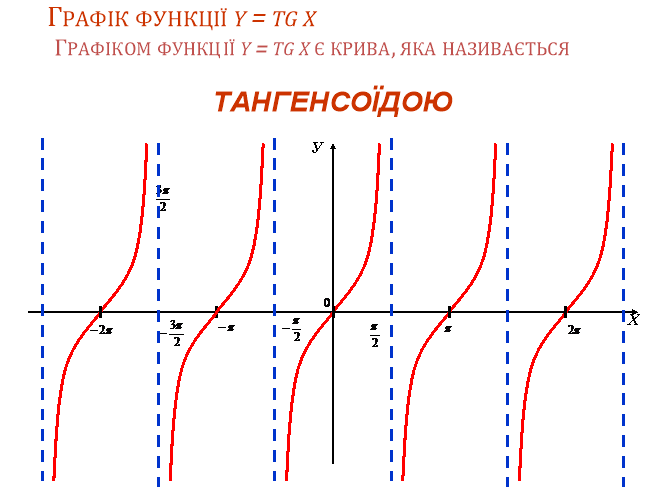
Для розв'язування деяких задач корисно мати уявлення про лінію тангенсів (рис.1 ). Проведемо дотичну t до одиничного кола в точці Ρо. Нехай α — довільне число, для якого cos α ![]() 0, тоді точка Рα (cos α; sin α) не лежить на осі ординат і пряма ОРα перетинає t в деякій точці Тα з абсцисою 1. Знайдемо ординату точки Тα із трикутника ОРоТα.
0, тоді точка Рα (cos α; sin α) не лежить на осі ординат і пряма ОРα перетинає t в деякій точці Тα з абсцисою 1. Знайдемо ординату точки Тα із трикутника ОРоТα.
![]() ; у = tgα.
; у = tgα.
Таким чином, ордината точки перетину прямих ОРα і t дорівнює тангенсу числа α. Тому пряму t називають віссю тангенсів.
Властивості вивчених тригонометричних функцій зручно записати в таблицю. При заповненні таблиці можливі такі коментарі:
Вираз tg х має смисл при будь-якому x, крім чисел виду х = ![]() , n
, n ![]() Ζ.
Ζ.
Оскільки tg α — це ордината точки ![]() лінії тангенсів, то областю значень тангенса є R.
лінії тангенсів, то областю значень тангенса є R.
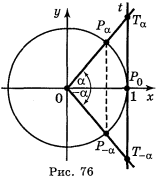
Оскільки точки Тα і Τ-α симетричні відносно Р0 лінії тангенсів, то tg (-α) = -tg α.
Можна довести аналітично, що tg α непарна функція:
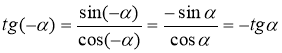 ,
,
При зміні кута α від -![]() до
до ![]() ордината точки Тα лінії тангенсів збільшується від -
ордината точки Тα лінії тангенсів збільшується від -![]() до +
до +![]() , тобто tg α зростає на проміжку
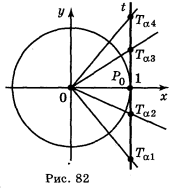
, тобто tg α зростає на проміжку ![]() . Враховуючи, що найменший додатний період тангенса є π, робимо висновок, що tg α зростає на кожному з проміжків
. Враховуючи, що найменший додатний період тангенса є π, робимо висновок, що tg α зростає на кожному з проміжків ![]() , п
, п![]() Ζ (рис. 82).
Ζ (рис. 82).
- Закріплення нового матеріалу.
7.1 Знайти область визначення функції
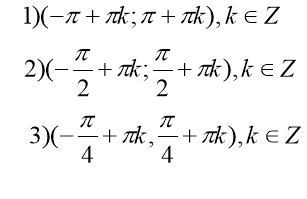
А)
![]()
Б)
![]()
В)
![]()
![]() 7.2. Дослідити функцію на парність (непарність):
7.2. Дослідити функцію на парність (непарність):
![]()
1)непарна;
2)ні парна, ні непарна;
3)непарна;
7.3 Виконання вправ на закріплення властивостей функції у=tqx
Вправа 1. Користуючись властивостями функції у= tg x, порівняйте числа:
- tg 150 і tg 1400
- tg (-1,2 p) і tg (-0,1p)
- і
Очікувана відповідь:
- tg250; tg650; tg150.
- tg(-1); tg(-3); tg(-2) .
- tg(-3); tg(-5); tg 3.
Вправа 2. Розташуйте числа в порядку їх зростання:
- tg250; tg650; tg150.
- tg(-1); tg(-3); tg(-2) .
- tg(-3); tg(-5); tg 3.
Очікувана відповідь:
- tg250; tg650; tg150.
- tg(-1); tg(-3); tg(-2) .
- tg(-3); tg(-5); tg 3.
Вправа 1 (пояснення)
Розв’язання
- Оскільки tg 1400= tg (900+500)= tg 500 і функція у= tg x зростає на проміжку (-p/2; p /2) і 150 < 500, то tg 150 < tg 500.
Отже, tg 150 < tg 1400.
- Оскільки tg (-1,2 p)=tg (-p - 0,2p) = tg (- 0,2 p) і функція у= tg x зростає на проміжку
(-p /2; p /2) і - 0,2 p < - 0,1 p, то tg (- 0,2 p) < tg (- 0,1 p) .
Отже, tg (- 1,2 p) < tg (- 0,1 p).
- Оскільки tg (10p/9)=tg (p + p/9) = tg (p/9) і функція у= tg x зростає на проміжку
(-p /2; p /2) і 2p/9 > p/9 , то tg 2p/9 > tg p/9 .
Отже, tg 2p/9 > tg 10p/9 .
-
Розминка
8. 1. Підняти праву руку перед собою, паралельно поверхні стола і виконати круговий
поворот на 720 градусів.
8. 2. Підняти ліву руку перед собою, паралельно поверхні стола і виконати круговий поворот на
(-1080) градусів.
8. 3. Покласти кисті рук на плечі і виконати по 4 кругових рухи вперед і назад. Яка сума кутів повороту?
-
Перетворення графіків функції y= tg x.
- Тренувальні вправи
(Метод: встановлення відповідностей)
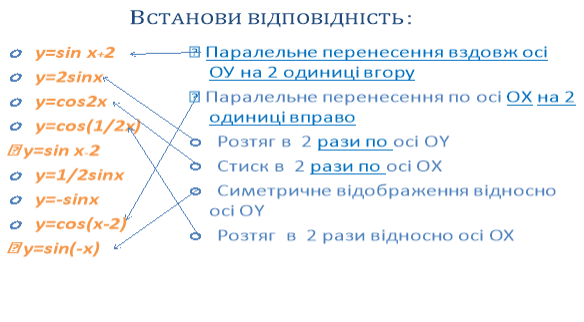
- Серед наведених графіків зазначте графік функції y=|tg x|
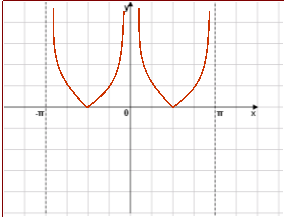

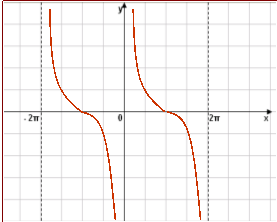
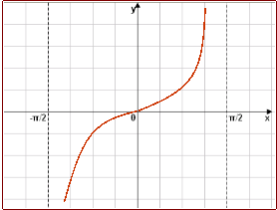
-
 Функція y=2tg x зростає на проміжку :
Функція y=2tg x зростає на проміжку :
А)
![]() Б)
Б)
![]()
В)
![]()
Г)
![]()
Д)
- Графік функції y = tgx паралельно перенесли на 2 одиниці вниз вздовж осі Oy і на π/4 одиниці вліво вздовж осі Ox. Отримали наступний графік функції:
![]()
А)
![]()
Б)
![]()
В)
![]()
Г)
- Самостійна робота.
№ 605. Побудувати графік функції.
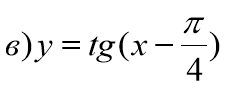
![]()
![]()
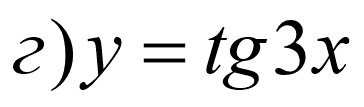
![]()
- Підведення підсумків заняття.( рефлексія)
Учням пропонується закінчити речення
- Сьогодні я дізналась…
- Було цікаво…
- Було важко…
- Я зрозуміла, що…
- Тепер я можу…
- Я навчилась…
- У мене вийшло…
- Я змогла….
- Мене здивувало…
- Урок дав мені для життя…
- Я випередила себе, вчорашню…
11. Оцінювання досягнень учнів.
12. Домашнє завдання.
1. А.Г. Мерзляк. Дидактичні матеріали. № 13, стр. 28
2. А.Г Мерзляк. Алгебра і початки аналізу. Розділ 4, §24, № 602(1,3,5), 604 (1), 605, 613 (на повторення).
1

про публікацію авторської розробки
Додати розробку
