Конспект уроку "Розв’язування рівнянь, що зводяться до квадратних", 8 клас

Тема: Розв’язування рівнянь, що зводяться до квадратних.

Мета:узагальнити та систематизувати знання  з теми;

продовжувати удосконалювати вміння та навики при розв’язуванні рівнянь, що зводяться до квадратних, поглибити вміння та навики при розв’язуванні дробово-раціональних рівнянь;

розвивати пізнавальну компетентність учнів, навички усного рахунку, увагу, пам'ять, логічне мислення;

виховувати інтерес до вивчення математики, творче ставлення до справи, цілеспрямованість, наполегливість, відповідальність,  уміння працювати в парі та групі.

Тип уроку: удосконалення, застосування знань і вмінь.

Хід уроку

І.Організаційний момент.

ІІ. Актуалізація опорних знань:

а)питання по домашньому завданню, наявність, відповіді;

б)повтор типів рівнянь, що зводяться до квадратних та короткий опис їх розв’язання:

І тип: (2х-4)(9-х)+22(9-х) = 0

ІІ тип: (3х-2)(х+6)-(х-2)(3-х) = 0

ІІІ тип: +-9 = 0

ІV тип:    =

в)самостійна робота з наступною взаємоперевіркою:

І варіант

1) (х-1)(х+2)+(х-1)(3+4х) = 0

2) -+4 = 0

ІІ варіант

1) (2,5х-7)(2х+3)+3х+4 = (4х-9)(1,5х+1)

2) =

ІІІ варіант

1) -20+64 = 0

2)  + = 12

ІІІ. Розв’язування  дробово-раціональних рівнянь.

1. 
2. 
3. 
4. .

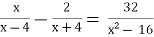
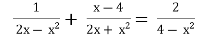
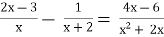Додаткові завдання:

1.  Знайти абсциси точок перетину  графіків функцій:

У =   і  у = .

2. За яких значень  х сума дробу 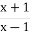      і  дробу, оберненого до даного, дорівнює 2,5.
3. За яких значень х  значення виразів рівні:

і    ?

IV. Підсумок уроку.

V. Домашнє завдання: повторити §24, §7, виконати №514 (3), ,  №516 (1).