Конспект уроку "Розв'язування задач" з теми "Теорема Піфагора"

Тема: Розв’язування задач

Мета: узагальнення знань учнів про прямокутний трикутник,    удосконалення вмінь розв’язувати задачі на теорему Піфагора,  розвиток обчислювальних навичок, інтересу до математики; виховання  мовної культури

 

 

 

 

Обладнання: презентація „Піфагор”, демонстрація „Піфагор”, таблиці самооцінювання.

Тип уроку: узагальнення знань, вмінь

 

 Хід уроку

І. Вступне слово вчителя

Прямокутний трикутник – одна з перших  геометричних фігур, про властивості якої людство дізналося ще в давнину. Задачі про трикутник знаходять у давньоєгипетських папірусах, старовинних індійських книгах. У папірусі Ахмеса згадується про властивості рівнобедреного та прямокутного трикутників, давні вавилоняни 4000 років тому вже знали про кути при основі рівнобедреного трикутника. Ознаки рівності трикутників були сформульовані Евдемом Родоським та Фалесом Мілетським. У давній Греції в іонійській математичній школі (заснована в VІ ст. до н.е. Фалесом ),  у школі Піфагора знали види і властивості трикутників. Систематизував ці відомості Евклід у першому трактаті з геометрії „Началах”.

Чому ж трикутник цікавив людей з давніх часів? Жорсткість трикутника використовувалася в будівництві й конструюванні, використовується і нині. Сьогоднішній  ми на уроці узагальнимо знання про прямокутний трикутник,  продовжимо розвивати вміння розв’язувати задачі на теорему Піфагора, продовжимо формувати та удосконалювати обчислювальні навички, дізнаємось цікаве з історії математики.

Наш урок буде відбуватися в вигляді подорожі, бо я дуже люблю подорожувати, пізнавати щось  цікаве на новому шляху. Я маю надію, що ви теж любите мандрувати і ми з вами подружимось.

ІІ. Актуалізація опорних знань учнів

Перевіримо готовність нашої команди.

Метод „Мікрофон”. Даєте відповідь на одне питання і передаєте мікрофон  наступному.

1. Трикутник, у якого є прямий кут, називається …(прямокутним)
2. Сторона прямокутного трикутника, що лежить проти прямого кута, називається …(гіпотенуза)
3. Перпендикуляр, проведений з вершини трикутника на протилежну сторону, називається …(висотою)
4. Відношення прилеглого катета до гіпотенузи в прямокутному трикутнику називається … (косинусом кута)
5. Відрізок, що сполучає основу перпендикуляра з основою похилої, називається … (проекція)
6. Рівні похилі мають … проекції (рівні)
7. З двох похилих більша та, у якої проекція … (більша)
8. Сформулюйте нерівність трикутника (В будь-якому трикутнику кожна сторона менша за суму двох інших сторін)

ІІІ. Сприймання і усвідомлення матеріалу

Наша подорож буде не лише в далекі країни, але й у далеке минуле.

І етап

острів Самос

Вирушаємо на острів Самос, де в 580 р. до н.е. народився давньогрецький математик Піфагор.

Шлях до нього нам вкажуть острівки. Усі острівки мають форму трикутників. Але деякі з них вводять нас в оману. Правильний шлях вкажуть нам лише прямокутні  трикутники.

 

 

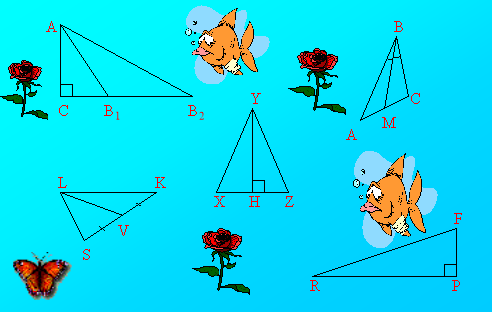
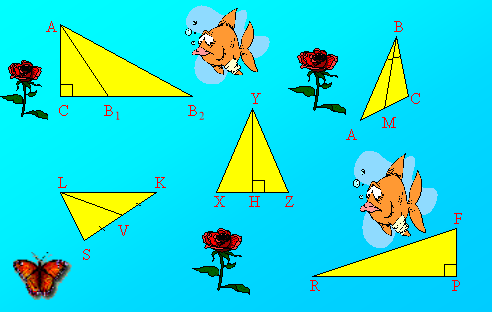
Ось ми на острові Самос, де народився,  найславетніший дав­ньогрецький матема­тик, філософ-ідеаліст Піфагор народився в 580 р. до н.е. на ос­трові Самосі. З цієї причини його називають Піфагором Самоським. До речі, існував ще один Піфагор з Самоса, він був відомим скульптором і нази­вався Регейським, бо працював у місті Регії. З ім'ям Піфагора пов'язано, мабуть, найбільше різних цікавих подій і легенд. Вже навіть саме ім'я цієї видат­ної людини незвичайне, бо во­но буквально означає «Той, про кого сповістила Піфія», тобто народження Піфагора було передбачено заздалегідь.

Легендарною особою Піфагора вважали вже у стародавні часи — у 306 р. до н.е. йому, як найрозумнішому з греків, поставили па­м'ятник на римському форумі перед коміцієм, вона простояла там до початку правління Сулли. А вперше слава прийшла до Піфаго­ра, коли він був ще ефебом (юнаком). У віці вісімнадцяти років він, за звичаєм багатьох молодих людей свого часу, починає подорожу­вати і перш за все їде до Мілету, щоб зустрітися з Фалесом. Фалес зустрів його ласкаво, щиро поділився своїми знаннями, але, жаліючись на старість і слабке здоров'я, порадив їхати до Єгипту, щоб ще повчитися у єгипетських жерців. Він також сказав, що ні від природи, ні внаслідок навчання не має такої вдачі, яку він ба­чить у Піфагора. Тому, спілкуючись з уславленими жерцями, Піфагор може стати найбільш близьким до богів і найбільш розум­ним серед людей.

 

ІІ етап

Єгипет

Піфагор вирушає до  Єгипту, і ми разом з ним. Щоб потрапити нам до цієї країни слід виконати завдання, яке і буде перепусткою до неї.

Тестова робота

 

 

 

 

 Єгипет – гаряча країна, тому в розподілі населення величезну роль відіграє клімат. Пустелі, екваторіальні терени заселені мало. Зате у вологих тропічних зонах та в долині Нілу люду мешкає значно більше. Ця одна з найбільших річок світу і манила до себе,  і завдавала багато клопоту. Бо коли Ніл розливався і виходив з берегів, то 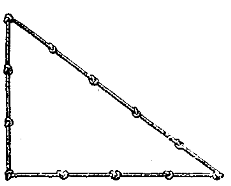руйнував житла єгиптян. Тому народ добре знався на будівництві і в математиці. Ще з часів подорожі Піфагора по Єгипту йому був відомий єгипетський трикутник  з сторонами 3,4,5. Єгипетські жерці свято берегли таємниці і розглядали кожну математичну істину як божественне откровення. Серед таких істин широкою популярністю користувалась і та, яка протягом ряду тисячоліть служила єгипетським будівельникам для відбудови житла. Для побудови прямих кутів вони використовували вірьовку, поділену вузлами на 12 частин. Якщо з цієї вірьовки скласти трикутник із сторонами 3, 4, 5 частин, то кут між ними, із сторонами 3 і 4 частини, буде прямим. Цікаво, що саме такі пропорції археологи знаходять у  розмірах тесаних  плит піраміди   Хефрена  (в Єгипті).

Піфагор провів у Єгипті і його святинях 22 роки, займаючись спостереженням зоряного неба і геометрією, осягнувши не уривка­ми і не поверхово всі таїнства богів. А в той час, коли Єгипет заво­ював перський цар Камбіз, Піфагор був серед тих, кого захопили у полон біля стін Великих пірамід. Але його слава як мудреця і ма­га була вже на той час настільки велика, що коли Камбіз дізнався, хто знаходиться серед його полонених, він наказав негайно звільнити Піфагора і вибачився перед вченим.

ІІІ етап

Вавилон

Після полону Піфагор переїздить. Назва цього міста зашифрована. Розв’язавши трикутники, знайдемо ключ до розв’язки.

 

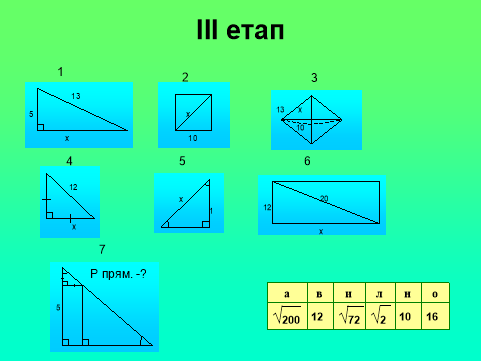
Після полону Піфагор перебуває у Вавилоні. Там він охоче спілкується з мудрецями і магами, які відповідали йому увагою, і, навчившись найго­ловнішому в їхньому вченні, глибоко опанувавши науку про числа, музику й інші предмети, провівши в такий спосіб ще дванадцять років.

 

 

ІV етап

Італія

Ми вирушаємо на південь Італії до м. Кротоні – грецької колонії. Поки ми не прибули до місця призначення погуляємо в гру „Вірю – не вірю”

Правила такі, якщо вам здається твердження правильним, то покажіть мені знак плюс, інакше – знак мінус.

Чи вірите ви:

1. Що  будь-який прямокутний трикутник називається єгипетським? (ні)
2. Що Піфагор брав участь у кулачному бої на олімпійських іграх? (Так, він був чемпіоном у цьому виді спорту)
3. Що Фалес був болільником і помер на трибуні Олімпійського стадіону під час бою Піфагора7 (Так)
4. Що якщо кожного дня по 10 годин просто переписувати праці Леонарда Ейлера, то не вистачить і 76 років, щоб переписати їх? (так, його праці складають 75 великих томів)
5. Що Шарль Перро, автор „Червоної шапочки”, написав казку „Кохання циркуля і лінійки”? (Так)
6. Що Наполеон Бонапарт писав математичні роботи? (так, відома задача Наполеона)
7. Що два в квадраті – 4, три в квадраті – 9, кут у квадраті 90? (так)
8. Що вперше розробив математичну теорію музики Піфагор? (так)
9. Що всі три сторони піфагорового трикутника визначаються непарними числами? (Ні, бо квадрат непарного числа є число непарне, а сума двох непарних чисел завжди число парне)

 

В місті Кротоні Піфагор розпочав свою діяльність. Його вважали пророком і тому діяльність школи, яку він заснував, носила таємничий характер.

Велику увагу піфагорійці  приділяли дослідженням властивостей прямокутних трикутників, сторони яких визначаються цілими числами. Теорема Піфагора була відома вавилонянам ще за 1200 років до Піфагора. Знали її й у стародавній Індії. Можливо, що Піфагор або його учні дали перше повноцінне доведення цієї теореми. Теорема Піфагора є одним з найважливіших геометричних тверджень. Відомо понад 150 способів доведення цієї теореми

 

 

V етап

Індія

Країна до берегів якої ми підпливаємо – стародавня Індія. Там у ХІІ ст. у книзі „Лілаваті” (що означає „Прекрасна”, мається на увазі наука арифметика) Бхаскара   так довів теорему Піфагора:

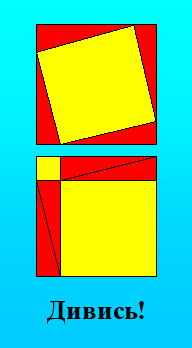
Розглядаючи ці два рисунки, видно, що сума квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі.

Цей індійський вчений запропонував нам задачу (задачі складались у віршованій формі, щоб краще запам’ятовувались):

На березі річки тополя росла,

Та вітру порив її стовбур зламав.

Тополя упала і стовбур її

Кут прямий з течією ріки утворив.

Пам’ятай, в тому місці ріка

Чотири фути була шириною.

Верхівка схилилась до краю,

Залишивши три фути всього над водою.

Прошу, тепер швидше скажи мені ти:

Тополя якої була висоти?  (5+3=8 футів)

 

Положення, які містилися в „Сутрах” мали зміст:

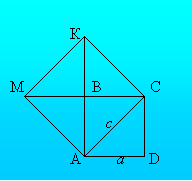
1. Квадрат діагоналі прямокутника дорівнює сумі квадратів його більшої і меншої сторін

АС² = АD² + СD²

 

 

2. Квадрат на діагоналі квадрата в два рази більший самого квадрата

VІ етап

Німеччина

Заглянемо до Німеччини .

Існує легенда про те, що в честь свого відкриття Піфагор приніс в жертву бика, або, як розповідають інші 100 биків, яка послужила приводом для гумору в творах письменників та у віршах поетів. Німецький письменник А.Шаміссо написав:

Пребудет вечной истина, как скоро

Её познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожжение

За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, её почуя, вслед.

Они не в силах свету помешать,

А могут лишь, закрыв глаза, дрожать

От страха, что вселил в них Пифагор.

 

ХV ст. з рукописного німецького трактату нам пропонують розв’язати задачу.

 Драбину завдовжки 13 футів приставили до стіни так, щоб нижня її частина була віддалена від стіни на 5 футів. На скільки опуститься драбина по стіні, якщо її основу відсунути ще на 7 футів?

 

 

VІІ етап

Греція

Ми наближаємось до нашого часу і тримаємо курс на Грецію. Там в  1955 році було випущено поштову марку,  що ілюструє теорему Піфагора.

Щоб її побачити треба справитись із завданням.

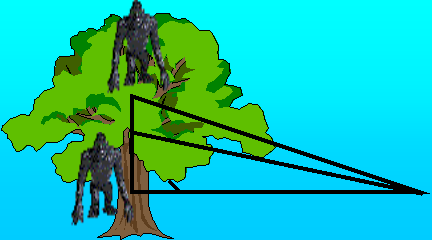
На дереві сиділо дві мавпи: одна — на самій вершині дерева, друга — на висоті 10 ліктів від землі. Другій мавпі захотілося напитися води з джерела, що було на відстані 40 ліктів від основи дерева, і вона злізла з дерева; за той самий час перша мавпа зскочила з вершини дерева просто до того самого джерела (рухаючись по прямій лінії). Обидві мавпи пройшли ту саму відстань. Швидко скажіть, з якої висоти стрибнула мавпа.

 

 

 

 

Дивлячись на неї, можна наочно пересвідчитися в тому, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів ка­тетів. Сума площ квадратів, побудованих на двох катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі. (9 + 16 = 25)

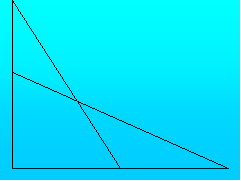
Малюнок для випадку рівнобедреного трикутника учні називали „піфагоровими штанами” і в дореволюційній Росії складали вірші:

„Пифагоровы штаны Во все стороны равны.”

 

 

VІІІ етап

Прилуки

І ось нарешті ми повернулися додому і потрапили на аукціон.

Ви вибираєте одну із  запропонованих задач і отримаєте бали:  10, 11, 12.

Задача 1. У пункті А дві траси перетинаються під прямим кутом. З цього пункту однозначно вирушили автомобіль зі швидкістю 80 км/год і автобус зі швидкістю 60 км/год. Яка відстань буде між ними через 3 год?

Задача 2. Катети прямокутного трикутника дорівнюють 12 м і 9 м. Знайдіть невідомі лінійні елементи трикутника.

Задача 3. Обчисліть висоту рівнобічної трапеції, у якої основи дорівнюють 24 см і 44 см  , а бічна сторона – 70 см.

 

 

ІV. Домашнє завдання: скласти задачу практичного змісту, для розв’язання якої треба використати теорему Піфагора.

V.  Підсумок уроку: оголошуються оцінки. Дякую класу за співпрацю.