Конспект уроку з алгебри і початків аналізу для 11-го класу на тему "Похідні елементарних функцій. Правила знаходження похідних."

Урок алгебри і початків аналізу  в 11 класі

Тема: Похідні елементарних функцій. Правила знаходження похідних

Мета:

      навчальна: працювати над засвоєнням учнями: правил обчислення похідних; змісту основних правил диференціювання та формулювання їх математичною мовою, домогтися свідомого сприйняття учнями змісту понять  «диференційована функція», «диференціальне числення», сформувати вміння знаходити похідні функцій, використовуючи правила знаходження похідних; продовжити формувати вміння та навички учнів застосовувати набуті знання до розв’язування задач з даної теми;

                     розвивальна: розвивати логічне  мислення,  комунікабельність, увагу, пам’ять, здатність до самостійності мислення; усне та писемне мовлення; розвивати інтерес до математики;

                    виховна:виховувати в учнів бажання мати глибокі й міцні знання, працьовитість та уважність; сприяти розвитку всесторонньо розвинутої особистості;

 

Тип уроку: засвоєння нових знань, умінь і навичок.

Хід уроку

І. Організаційний етап.

Організація уваги учнів. Перевірка готовності класу до заняття.

Для сьогоднішнього уроку я до кожного етапу уроку підібрала вислів відомої людини. І починаємо ми з вислову Конфуція « Від того настрою, з яким ви вступаєте в день, або в якусь справу залежать ваші успіхи, а можливо, і невдачі». Я бажаю вам розпочати урок з гарним настроєм і отримати від нього задоволення і гарні результати.

ІІ. Перевірка домашнього завдання.

«Як приємно дізнатися, що ти чогось навчився». Мольє

Звіримо відповіді

№210

А) 45 ; Б) -2; В) 0

№219

А) 0; Б) 1/7.

№ 249

А) 5; Б) -5; В) 2

ІV.  Актуалізація знань, умінь та навичок.

Хай живе теорія – без теорії немає практики.

1. Символом  ∆х позначають?  (приріст аргументу)

2.  Символом  ∆ƒ, ∆у позначають ?  (приріст функції)

3.  Границя неперервної функції дорівнює ? (значенню функції в цій точці)

4. Похідною функції ƒ(х) у точці х₀  називають? 

5. Сформулюйте геометричний зміст похідної? (похідна функції в точці дорівнює кутовому коефіцієнту дотичної до графіка даної функції в даній точці)

6.  Знайти f'(x₁),f'(x₂)

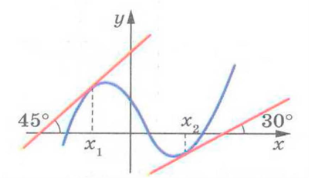
7. Знайти похідні функцій

1) y=5;  2)  y=x ; 3) y=x²; 4) y=x³ ; 5) ; 6) .

ІІІ. Формування теми та мети уроку.

«Коли починаєш справу, спитай себе: «Що я маю зробити?» Після закінчення: «Що я зробив?» Піфагор.

Тема нашого уроку: Похідні елементарних функцій. Правила знаходження похідних

План нашого уроку:

1.Таблиця похідних.

2. Похідна одночлена.

3.Похідна суми.

4.Похідна добутку.

5.Похідна частки.

 

ІV.  Мотивація навчальної діяльності.

«Математику вже навіть задля того потрібно вивчати, що вона розум  до ладу приводить». Ломоносов

Сучасні фахівці повинні добре володіти математичним апаратом, який має надзвичайне значення для багатьох професій.

V.  Вивчення  нового матеріалу.

1.Таблиця похідних.

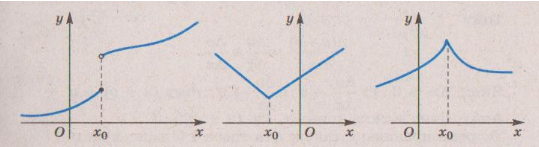
Чи кожна функція має похідну в кожній точці?

Функції не мають похідних в точках розриву, в точках зламу та в кінцевий точках області визначення функції.

 

 

 

 

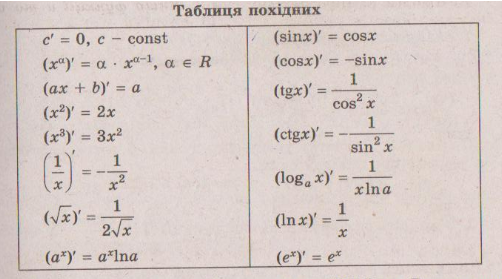
Ми розглядатимемо функції, графіки яких – неперервні лінії. Операцію визначення похідної функції називають диференціюванням.

 

 

 

 

 

 

 

 

Це формули за допомогою яких знаходять похідні даних функцій.

Кожна з цих формул доведена у XVII ст.

2. Похідна одночлена.

Для кожного натурального n і дійсного k в кожній точці x:

,

де  n – натуральне число, k – дійсне число

Приклад.

;

.

Усно:

=

=

=

3.Похідна суми.

Якщо функція u та v диференційовані в точці x, то в цій точці

.

Приклад

;

4.Похідна добутку.

Якщо функція u та v диференційовані в точці x, то .

Приклад

;

5.Похідна частки.

Якщо функція u та v – функція від x, диференційовані в точці x, причому в цій точці , то

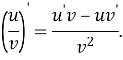
Приклад

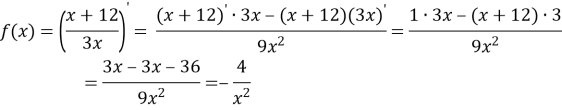
Розв’язування вправ

№ 267 – а), б),  г), д) – самостійно

Біля дошки

№ 271, № 275 – а), б), в);

Тест з ЗНО 2009 року

Хвилина релаксації (звучить спокійна музика)

№ 289 – а);

№ 296 – а);

№ 298 – б);

№ 299 – а).

VІІІ. Домашнє завдання.

«Як крапля довбає камінь не силою, а частим падінням, так і людина стає вченою частим учінням». Дістервег.

Вивчити п. 8 (Г.П. Бевз, В.Г. Бевз Математика 11 клас, Київ «Генеза» 2011)

№ 272; №281; №299 - г)

ІХ. Рефлексія.

Для взаємозв’язку вчителя з учнями використовується прийом «Скринька побажань».

Що сподобалося на уроці?

Що не сподобалося?

Що пропонуєш змінити?

Учні пишуть відповіді на аркушах і кладуть до скриньки.

Закінчити наш урок мені хотілося б словами Спінози: «Якщо ви хочете, щоб життя посміхалося вам, подаруєте йому спочатку свій гарний настрій».

Дякую вам за урок. Бажаю всім успіхів і гарного настрою!