Конспект уроку з алгебри на тему: "Сума n перших членів арифметичної прогресії."
Конспект уроку алгебри в 9 класі
студентки групи МІЕ17Б Чудної Олени
Тема: Сума n перших членів арифметичної прогресії.
Мета:
-
Навчальна:
- повторення та закріплення основних понять, властивостей з даної теми;
- формування вмінь застосовувати властивості арифметичної прогресії до розв’язування вправ, знаходити суму n перших членів арифметичної прогресії
-
Виховна:
- виховувати пізнавальний інтерес до математики
- виховувати інтерес до знань;
- виховувати наполегливість.
-
Розвиваюча:
- розвивати вміння використовувати теоретичні знання на практиці;
- розвивати навички логічного мислення;
- розвивати вміння аналізувати, узагальнювати, порівнювати, робити висновки
Тривалість уроку : 45 хвилин
Тип уроку: урок формування умінь та навичок з теми.
Етапи уроку
- Організаційний момент (2 хвилини)
- Перевірка домашнього завдання (5 хвилин)
- Актуалізація опорних знань та мотивація навчальної діяльності учнів (10 хвилин)
- Виконання практичних завдань (26 хвилин)
- Підсумок уроку (2 хвилини)
- Постановка домашнього завдання (2 хвилини)
Хід уроку
І. Організаційний момент.
Доброго дня, діти! Сподіваюсь ви відпочили на перерві? Ну, що ж зараз час налаштуватися на урок. Давайте перевіримо чи всі присутні на уроці. (Вчитель за журналом відмічає присутніх та відсутніх).
ІІ. Перевірка домашнього завдання.
Підручник: Алгебра: підруч. для 9-го кл. загальноосвіт. навч. закл./ О.С. Істер. – Київ: Генеза, 2017. – 264 с.
№729
Знайдіть ![]() – суму десяти перших членів арифметичної прогресії (
– суму десяти перших членів арифметичної прогресії (![]() якщо
якщо ![]() .
.
Розв’язання
![]()
![]()
Відповідь: ![]()
№731
Знайдіть суму двадцяти перших членів арифметичної прогресії (![]() якщо
якщо ![]() .
.
Розв’язання
![]()
![]()
Відповідь: ![]()
№733
Знайдіть суму тридцяти перших членів арифметичної прогресії:
- 5; 8; 11;…
- 0; -2,5; -5;… .
Розв’язання
![]()
- 5; 8; 11; …
Щоб знайти суму, спершу знайдемо різницю прогресії:
![]()
![]()
![]()
- 0; -2,5; -5;…
Щоб знайти суму, спершу знайдемо різницю прогресії:
![]()
![]()
![]()
Відповідь: 1) ![]() 2)
2) ![]()
№735
Знайдіть суму вісімдесяти перших членів арифметичної прогресії ![]() , якщо
, якщо ![]()
Розв’язання
Знайдемо ![]() та
та ![]() :
:
![]()
![]()
![]()
![]()
Або
Знайдемо ![]()
![]()
![]()
Знайдемо d:
![]()
![]()
![]()
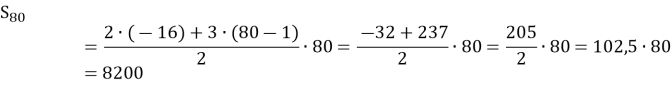
Відповідь: ![]()
ІІІ. Актуалізація опорних знань та мотивація навчальної діяльності учнів
На попередніх уроках ми з вами знайомилися арифметичною прогресією та її властивостями. Арифметична прогресія зустрічається насправді дуже часто в нашому житті. Наприклад, у вавилонських текстах розповідається про те, що збільшення освітленої частини місячного диска протягом перших п'яти днів відбувається за законом геометричної прогресії, з якою ми познайомимося трохи пізніше, а наступні 10 днів - за законом арифметичної прогресії з різницею 16.
Сьогодні ж я пропоную, вам набути нових умінь у розв’язуванні задач із знаходження суми n перших членів арифметичної прогресії.
Та перш ніж розпочинати виконувати завдання нам треба пригадати теоретичний матеріал, для цього ми проведемо невеличкий математичний диктант:
- Послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число називають…(арифметичною прогресією).
- Якщо d > 0, то арифметична прогресія … (зростаюча), якщо d < 0, то прогресія … (спадна).
-
Характеристична властивість, формула (
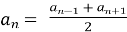 ).
).
-
Як виражається n-й член арифметичної прогресії через її перший член і різницю? (
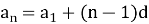 ).
).
-
Чому дорівнює сума n перших членів арифметичної прогресії? (
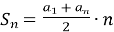 ,
, 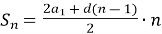 ).
).
Обміняйтеся зошитами та перевірте один одного. (виводиться слайд)
Добре, ми все пригадали, тепер можна перейти й до практики.
ІV. Виконання практичних завдань.
№740
Знайдіть суму:
- усіх натуральних чисел від 125 до 317 включно;
- усіх натуральних чисел, які кратні числу 5 і не більші за число 350;
- усіх двоцифрових натуральних чисел які при діленні на 3 дають в остачі 2 (необов’язково, в залежності від рівня знань учнів в класі).
Розв’язання
Для того щоб знайти суму, спершу знайдемо кількість членів прогресії:
![]()
![]()
![]()
- В даному випадку, послідовність матиме вигляд 5; 10; 15; …
![]()
![]()
З’ясуємо кількість членів прогресії:
![]()
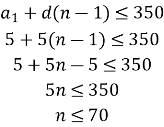
Отже, ![]()
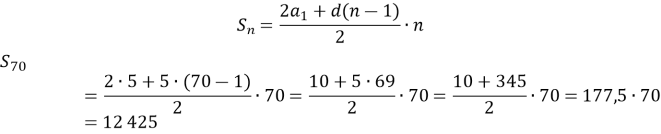
-
Нам треба підібрати таку послідовність двоцифрових натуральних чисел, які б при діленні на 3 давали остачу 2.
Такими числами будуть 11; 14; 17; …
Чому так? Міркування такі: 9 ділиться на 3 без остачі, а щоб остача складала 2, треба до 9 додати 2 й отримаємо 11. Аналогічно діяли далі, 12![]() 3, щоб остача була рівною 2, додамо 12+2=14. І так далі.
3, щоб остача була рівною 2, додамо 12+2=14. І так далі.
Щоб з’ясувати чому дорівнює ![]() , дивимось які числа (близькі до 100) ділять на 3 без остачі. Це 96 і 99, але щоб остача була 2, до них треба додати 2 і отримаємо 98 і 101 відповідно. Нам підійде 98. Отже,
, дивимось які числа (близькі до 100) ділять на 3 без остачі. Це 96 і 99, але щоб остача була 2, до них треба додати 2 і отримаємо 98 і 101 відповідно. Нам підійде 98. Отже, ![]()
Знайдемо d:
![]()
![]()
Знайдемо n:
![]()
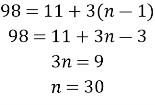
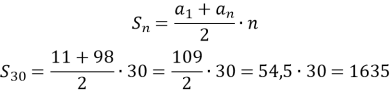
Відповідь: 1) ![]()
№742
Знайдіть суму восьми перших членів арифметичної прогресії ![]() , якщо:
, якщо:
Розв’язання
![]()
- Знайдемо d:
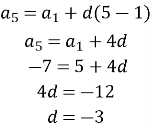
![]()
- Знайдемо d:
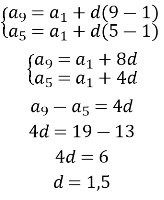 Знайдемо
Знайдемо ![]()
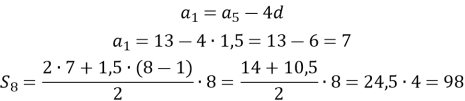
Відповідь: 1) ![]()
№744
Знайдіть перший член арифметичної прогресії, якщо сума перших п’ятнадцяти членів цієї прогресії дорівнює 375, а різниця прогресії дорівнює 3.
Розв’язання
Отже, з умови маємо, що
![]()
Суму можна знайти за такою формулою:
![]()
З неї й знайдемо ![]() , підставивши у формулу відомі нам значення:
, підставивши у формулу відомі нам значення:
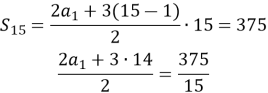
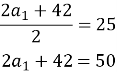
![]()
![]()
Відповідь: ![]() .
.
№746
Знайдіть суму додатних членів арифметичної прогресії 19; 17; 15; … .
Розв’язання
Знайдемо d:
![]()
![]()
Знайдемо порядковий номер n останнього додатнього члена послідовності:
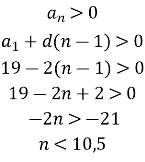 Так як n має бути додатнім, то n=10.
Так як n має бути додатнім, то n=10.
Отже, ![]() останній додатній член послідовності. Тому, шукаємо
останній додатній член послідовності. Тому, шукаємо ![]()
![]()
![]()
Відповідь: ![]()
V. Підсумок уроку
Ми з вами добре постаралися, ви всі молодці. Тепер ви точно впевнилися, що математика це неабияка гімнастика для нашого розуму.
- Чи були у вас труднощі у виконанні завдань? (Так/Ні)
- Які труднощі у вас виникали?
VІ. Постановка домашнього завдання
Дякую вам за увагу та активність на уроці, а тепер запишіть домашнє завдання: №741(1), 743, 745, 747 (Алгебра: підруч. для 9-го кл. загальноосвіт. навч. закл./ О.С. Істер. – Київ: Генеза, 2017. – 264 с.)
№741 (1)
Знайдіть суму:
- Усіх натуральних чисел, які кратні числу 7 і не перевищують числа 420.
Розв’язання
В даному випадку, послідовність матиме вигляд 7; 14; 21; …
![]()
![]()
З’ясуємо кількість членів прогресії:
![]()
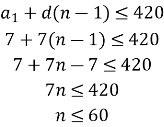
Отже, ![]()
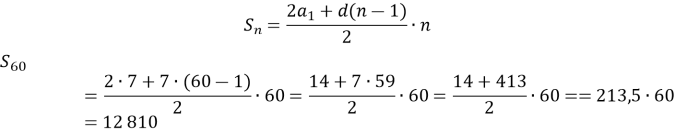
Відповідь: ![]()
№743
Знайдіть суму десяти перших членів арифметичної прогресії ![]() , якщо:
, якщо:
Розв’язання
![]()
- Знайдемо d:
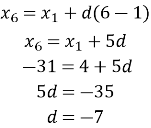
![]()
- Знайдемо d:
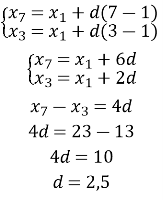 Знайдемо
Знайдемо ![]()
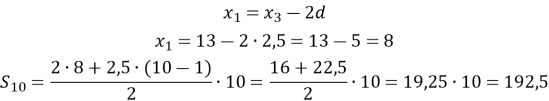
Відповідь: 1) ![]()
№745
Знайдіть різницю арифметичної прогресії ![]() , якщо
, якщо ![]() , а сума восьми її перших членів дорівнює 168.
, а сума восьми її перших членів дорівнює 168.
Розв’язання
Отже, з умови маємо, що
![]()
Суму можна знайти за такою формулою:
![]()
З неї й знайдемо ![]() , підставивши у формулу відомі нам значення:
, підставивши у формулу відомі нам значення:
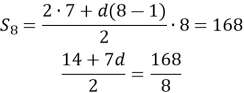
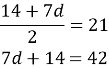
![]()
![]()
Відповідь: ![]() .
.
№747
Знайдіть суму від’ємних членів арифметичної прогресії ![]()
Розв’язання
Знайдемо d:
![]()
![]()
Знайдемо порядковий номер n останнього від’ємного члена послідовності:
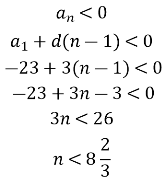 Так як n має бути додатнім, то n=8.
Так як n має бути додатнім, то n=8.
Отже, ![]() останній від’ємний член послідовності. Тому, шукаємо
останній від’ємний член послідовності. Тому, шукаємо ![]()
![]()
![]()
Відповідь: ![]()

про публікацію авторської розробки
Додати розробку
