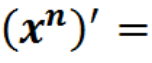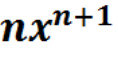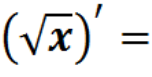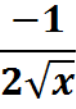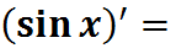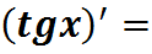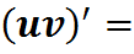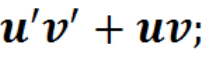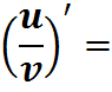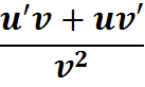|
Узагальнюючо-підсумковий урок по темі “Похідна функції”.
Тема уроку. Похідна. Фізичний і геометричний зміст похідної.
Мета уроку:
-
Продовжувати формувати навики застосування формул і правил диференціювання при розв'язуванні вправ, підготувати учнів до контрольної роботи.
-
Розвивати логічне і системне мислення, комунікабельність.
-
Виховувати прагнення до поглиблення та удосконалення знань.
Математику не можна вивчати спостерігаючи, як це робить сусід!
А. Нівен
Хід уроку
І. Мотивація навчальної діяльності. Формулювання цілей та завдань уроку
Похідна – фундаментальне поняття математичного аналізу за допомогою якого досліджують процеси і явища в природних , соціальних і економічних науках. Тому вивченню цієї теми ми приділили особливув увагу. Продовжуємо роботу.
Основна мета нашого уроку – використання теоретичних знань при розв’язанні практичних задач. Ключова ціль –впевнено себе почувати під час контрольної роботи та ЗНО де досить прості в розв’язанні задачі мають достатньо нестандартний зміст.
ІІ. Актуалізація опорних знань
Історична довідка:
-
До відкриття похідної незалежно один від одного прийшли два відомих учених – І. Ньютон і Г. Лейбніц наприкінці XVII ст.
 
І. Ньютон сформулював і розв’язав основну проблему математичного аналізу: “ За даною довжиною шляху в будь-який момент часу знайти швидкість руху у вказаний час.” І якщо він виходив із задач механіки, то Г. Лейбніц – із геометричних задач. У Лейбніца первісним поняттям для похідної була дотична, а у Ньютона – швидкість.
ІІІ. Розв'язування вправ
Знання таблиці і правил – це надійний крок до розв’язання багатьох задач.
Усне опитування:
-
означення похідної;
-
правила диференціювання;
-
усне виконання завдань:
-
Знайти і виправити помилки
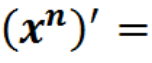 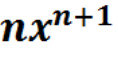
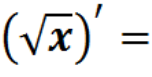 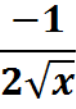
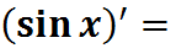 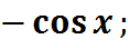
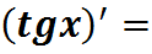 
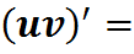 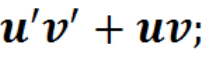
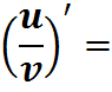 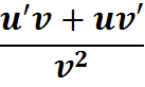
Знайти похідні функцій:
Виконання тестів - надійний шлях до здачі ЗНО
Завдання у форматі ЗНО


ІV. Творче перенесення знань та навичок у нові умови. Ґрунтовні знання з теми “Похідна” допоможуть Вам без проблем розв’язувати будь-які задачі, пов'язані з похідною.
-
Запишіть рівняння дотичної до графіка функції
у = х2 – х + 3, яка паралельна прямій х + у + 3 = 0.
2.Тіло рухається за законом S(t)= 1 + 2t2
(S – шлях у метрах t – час у секундах). Обчисліть швидкість руху в момент t0 =2с
3. Знайдіть кутовий коефіцієнт дотичної до параболи у = - х2 + х в точці з абсцисою х0 = 1.
4. Знайдіть, при яких значеннях параметра а дотична до графіка функції
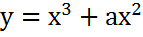
у точці з абсцисою х =-1 проходить через точку М(3;4).
Розв’язання
у=f(x )+f )+f (x (x )(x-x )(x-x ) )
f(x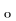 )=-1+а, )=-1+а,
f (x)=3x+2ax, (x)=3x+2ax,
f (-1)=3-2а, (-1)=3-2а,
у=-1+а+(3-2а)(х+1);
у=(3-2а)х-а+2;
т. М є у, то 4=(3-2а)3-а+2;
а=1.
Задача 5.
При яких значеннях параметра а дотичні до графіка функції у(х)=х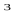 - а - а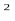 х проведені через точки з абсцисами х=0 і х=а перпендикулярні? х проведені через точки з абсцисами х=0 і х=а перпендикулярні?
Розв’язання
-
у (х)=3х (х)=3х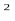 -а -а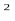 ; ;
у (0)=-а (0)=-а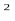 ; ;
у (а)=2а (а)=2а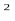 ; ;
дотична в точці з абсцисою х=0: у= -а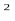 (х-0)=-а (х-0)=-а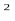 х; х;
дотична в точці з абсцисою х= а: у= а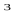 -а -а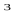 +2а +2а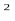 (х- а); (х- а);
у=2а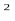 х-2а х-2а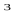 . .
-
k
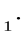 k k =-1-умова перпендикулярності прямих, отже маємо: =-1-умова перпендикулярності прямих, отже маємо:
-а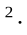 2а 2а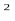 =-1, 2а =-1, 2а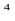 =1, а =1, а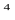 =0,5 ; а= =0,5 ; а=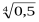
V. Підсумок уроку
Домашнє завдання:
Тестові завдання 1-12, с.150
|