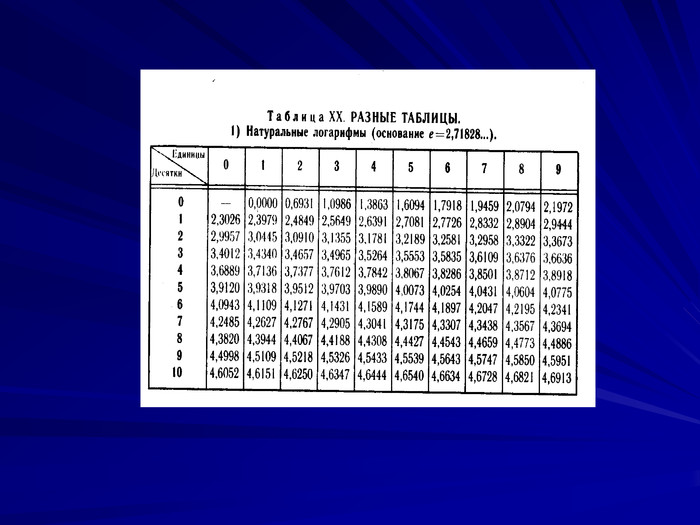
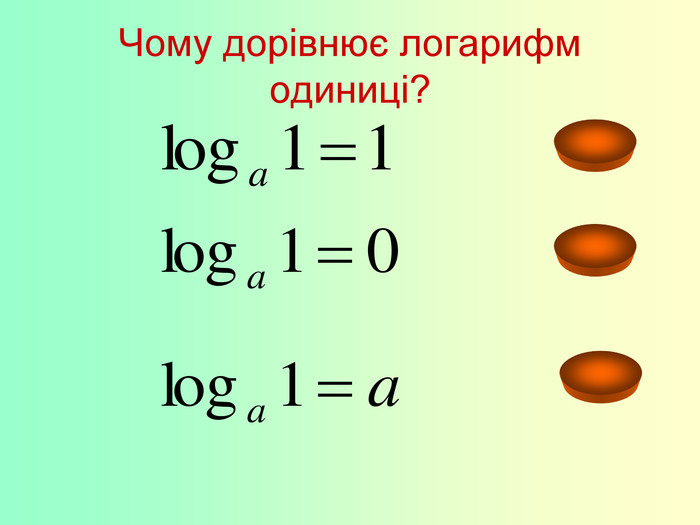Розробка уроку-гри на тему "Логарифмічна функція.Основні властивості логарифмів"
- îôçêèÇ_åêéÄÅêæ.ppt ppt
- ΓÑßΓ.ppt ppt
- ІСТОРІЯ ЛОГ.ppt ppt
- Логарифмічна функція.docx docx
- Показати всі файли
Логарифмічна функція.Основні властивості логарифмів
Вид уроку: узагальнення та систематизація знань (урок-змагання)
Мета:
1. Навчальна: Повторити і закріпити поняття логарифма числа, його основні властивості. Навчити учнів застосовувати свої знання, отримані на попередніх уроках при розв’язуванні задач підвищеної складності.
2. Виховна: Сприяти формуванню наукового світогляду учнів, виховувати культуру спілкування, взаємодопомоги, взаємної відповідальності при роботі в групах.
3.Розвиваюча: Розвивати творче мислення, математичну мову, вміння виражати свої думки та вислуховувати інших, розвивати самостійність в отриманні знань
Методичне та матеріальне забезпечення уроку: роздатковий матеріал,
мультимедійний проектор, екран, комп’ютер, учнівські презентації
Програмне забезпечення: Microsoft Office - 2003 (Microsoft Word, редактор формул ![]() , Power Point).
, Power Point).
Ресурси Інтернету: http://www.yandex.ru/ (пошук картинок застосування логарифмічної спіралі, пошук історичної довідки про відкриття логарифма і його першовідкривачів; пошук ескізів графіків логарифмічної функції).
Міжпредметна інтеграція: фізика, астрономія, біологія, історія математики, музика
Основні знання і вміння:
Знати: означення та властивості логарифмів, логарифмічної функції, методи розв’язування рівнянь
Вміти: логарифмувати алгебраїчні вирази, використовувати властивості логарифмів при обчисленні виразів, що містять логарифми, застосовувати свої знання при розв’язуванні задач підвищеної складності
Методична спрямованість: доцільність використання сучасних інформаційних технологій на уроці, демонстрація міжпредметних зв’язків
Хід уроку
І. Організаційний момент , перевірка д/з
Перевірка готовності учнів до уроку.
ІІ. Мотивація навчальної діяльності учнів, повідомлення теми, мети і завдань
Початок XX століття. Франція. Париж. Проходячи площею Екзюпері, пан Команьон вказав на будинок Денізо: «Щось більше не чути про провидицю, що спілкувалася з духами. Мене водив туди Лакарель, правитель канцелярії префекта. Вона сиділа в кріслі, заплющивши очі, а людей десять шанувальників ставили питання. На всі питання вона відповідала в поетичному стилі і без особливих труднощів. Коли черга дійшла до мене, я поставив найпростіше запитання: «Який логарифм 9?». Вона мені нічого не відповіла. Як же так? Провидиця і не знає логарифма 9? Та чи можливо таке! Всі були збентежені. Я пішов, і мене проводжали загальним несхваленням».
«Ох, знову логарифми», - подумаєте ви. А мені хочеться сказати: «Ах, ці логарифми». І сьогодні на занятті ми продовжимо відпрацьовувати навики знаходження логарифмів, але завдання будуть підвищеної складності, а також розглянемо застосування логарифмічної функції в самих різних областях науки і техніки.
ІІІ. Актуалізація опорних знань
Актуалізація опорних знань відбувається у вигляді математичної розминки. Формуються імпровізовані команди. Команда складається з 4 – 6 чоловік. Вчитель пояснює правила гри.
Запитання для команд
- У вигляді усного тесту (правильна відповідь 1 бал), завдання на екрані:
- Дайте означення логарифма
- Виберіть основну логарифмічну тотожність
- Чому дорівнює логарифм добутку?
- Чому дорівнює логарифм частки?
- Який логарифм називається десятковим?
- Який логарифм називається натуральним?
- Чому дорівнює логарифм степеня?
- Виберіть вірну рівність з даних
- Вкажіть формулу переходу до нової основи
-
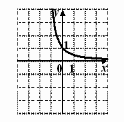
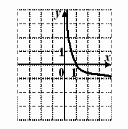
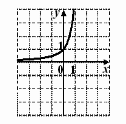
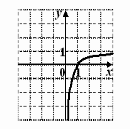
На одному з рисунків зображений ескіз графіка функції
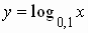 . Вкажіть номер цього рисунка.
. Вкажіть номер цього рисунка.
|
1) |
|
2) |
|
3) |
|
4) |
|
2.Завдання з ключем(за кожну правильну відповідь 1 бал): Цей прийом прийшов до нас з програмування і полягає в наступному: я вимовлятиму деякі твердження і, якщо ви згодні зі мною, то в зошиті ставите «1», якщо не згодні – «0». В результаті повинно вийти число.
-
Якщо
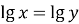 , то x = y
, то x = y
-
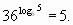
-
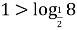
-
Якщо
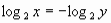 , то x = -y
, то x = -y
-
Графік функції y = x i
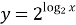 співпадають
співпадають
-
Якщо
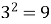 , то
, то 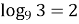
-
Область визначення функції
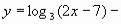 проміжок (0;
проміжок (0; 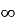 )
)
-
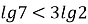
-
Якщо
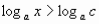 , то
, то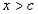 при
при 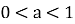
-
Вираз
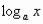 справедливий для будь-якого
справедливий для будь-якого 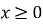
Ключ: 1010000100.
3.Вгадайте дати народження видатних математиків(8 балів)
Кожна команда отримує по чотири приклади, серед розв’язків яких вибирає натуральні числа від 1 до 9. Чотири розв’язки утворюють дату народження одного з великих математиків. Якщо команда після підказки вгадує ім’я математика їй нараховують додаткові бали (2 бали)
|
№1
а)
б)
в)
г)
а) 1; б) 5; в) 9; г) 6. |
№2
а)
б)
в)
г)
a) 1; б) 6; в) 2; г) 3. |
№3
а)
б)
в)
г)
a ) 1; б) 6; в) 4; г)3. |
№4
а)
б)
в)
г)
a ) 1; б) 5; в)5; г) 0. |
![]() Рене Декарт (1596-1650), французький філософ, математик, фізик і фізіолог.
Рене Декарт (1596-1650), французький філософ, математик, фізик і фізіолог.
Його латинізоване ім’я Картезій. Один з найвідоміших його висловів: cogito ergo sum- «думаю, значить, існую». Ці три короткі слова надовго визначили шлях «нової філософії»-поняття, яке стало рубежем між античністю і системним науковим мислителем середньовіччя. Його ім’ям названо прямокутну систему координат.
З ним була завойована свобода, позбутися якої філософія вже не могла.
Ісаак Ньютон (1643-1727), англійський математик, механік, астроном
і фізик.
Крім наукового таланту, йому були притаманні порядність і серйозне відношення до справи. Саме за ці якості він був призначений наглядачем Монетного двору. Крок за кроком він розібрався не тільки в технології виготовлення грошей, але й досконало вивчив методи, якими користувались фальшиво-монетчики і інші авантюристи. Озброєний цими знаннями, він розкрив діяльність більше 100 шахраїв і віддав іх під справедливий суд. В подяку від керівництва в 1699 році він отримав довічне високооплачуване звання директора Монетного двору. Він народився таким маленьким, що його можна було б викупати в пивній кружці
Блез Паскаль (1623-1662), французький філософ, письменник, математик і фізик.
Його життя одне з найяскравіших і трагічніших в історії людства. Якщо про якусь дитину можна сказати – вундеркінд, так це про нього. В 12-річному віці він по-новому відкрив початки евклідової геометрії. Математичні проблеми, на розв′язання яких древні геометри витратили кілька тисячоліть, юнаком були розв′язані за декілька днів. Це Гоголь в науці. Та ж безмежна талановитість, незвичайна творча щедрість і те ж перекреслення самого себе, якого не зміг перенести його геній.
Джон Непер( 1550-1617)
Він шотландець. У 16 років відправився на континент, де протягом п'яти років в різних університетах Європи вивчав математику і інші науки. До ідеї логарифмічних обчислень прийшов ще в 80-х роках 16 століття, проте опублікував свої таблиці тільки в 1614г., після 25-річних обчислень! Вони вийшли під назвою «Опис чудових логарифмічних таблиць». Цьому вченому належить і сам термін «логарифм», який він переводить як «штучне число».
4. Логарифмічна комедія : 2>3 (3 бали)
Розглянемо нерівність ![]() Вона вірна.
Вона вірна.
Замінимо кожен дріб степенем за основою ![]() :
: ![]()
Теж вірна нерівність. Більшому числу відповідає більший логарифм, значить
![]() тобто
тобто ![]()
Скоротимо на ![]() Отримуємо
Отримуємо ![]() .
.
В чому помилка цього доведення? (Помилка доведення полягає в тому, що число ![]() - від’ємне, а при діленні на від’ємне число – знак нерівності потрібно змінити на протилежний.)
- від’ємне, а при діленні на від’ємне число – знак нерівності потрібно змінити на протилежний.)
5. «Будь-яке число – трьома двійками»(3 бали)
Продовжимо уроку дотепною головоломкою алгебри, якою розважалися учасники одного з'їзду фізиків в Одесі. Пропонується завдання: будь-яке дане число, ціле і додатне, зобразити за допомогою трьох двійок і математичних символів.
Наприклад: Нехай дано число 3.
Розв’язання:
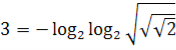 ,
,
Так як 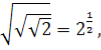
![]() ,
, ![]() .
.
Аналогично: 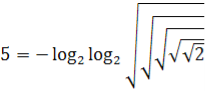 .
.
IV Основна частина. Виконання вправ
Логарифмічні дива
Розв’яжемо декілька прикладів:
-
Обчислити
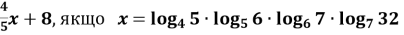 (5б)
(5б)
Розв’язання:
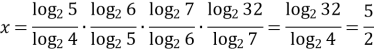
![]()
-
Знайти з рівності x:
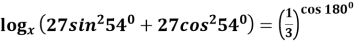
(5б)
-
Порівняти числа А =
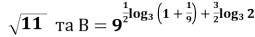
(7б)
Розв’язання:
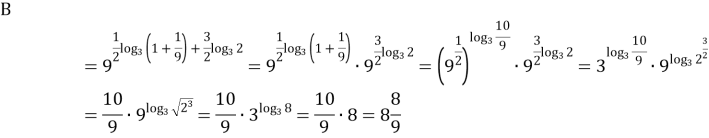
Отже, В >A
-
Розв’язати рівняння:
 (7б)
(7б)
Розв’язання:
![]()
![]() =lg100
=lg100
![]() - 2=0
- 2=0
![]()
Перевірка
Відповідь: x=100, x=0,1
-
Побудувати графік функції:
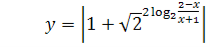 (10 б)
(10 б)
Розв’язання:
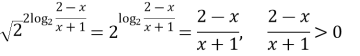
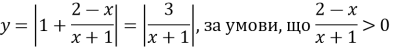
Розв’яжемо нерівність: ![]()
![]()
![]()
Будуємо графік ![]() в системі
в системі ![]() , де
, де ![]() (-1;0)
(-1;0)
V Презентації учнів
Логарифми, як і багато математичних понять, мають давню історію. Розширимо свої знання про них .
1.Історія виникнення логарифмів
2. Логарифмічна спіраль.
3. Зірки, шум і логарифми
4. Музика, живопис, архітектура і логарифми.
VI Підсумок уроку
Ода експоненті.
Дійсно, безмежні застосування логарифмічної функцій в самих різних областях науки і техніки, адже придумували логарифми для полегшення обчислень. Більше трьох століть пройшло з того дня, як в 1614 році були опубліковані перші логарифмічні таблиці, складені Джоном Непером. Вони допомагали астрономам і інженерам. Скорочуючи час на обчислення, тим самим, як сказав знаменитий французький вчений Лаплас: “Подовжуючи життя астрономам (обчислювачам)”.
Все це надихнуло англійського поета Ельмера Бріла, який написав “оду експоненті”. Уривок з якої ми наводимо:
“…Ею порождено многое из того,
Что достойно упоминания,
Как говорили наши
Англосаксонские предки:
Могущество ее порождений
Заранее обусловлено ее
Собственной красотой и силой,
Ибо они суть физического воплощения
Абстрактной идеи ее.
Английские моряки любят и знают ее
Под именем “Гунтер”.
Две шкалы Гунтера-
Вот чудо изобретательности.
Экспонентой порождена
Логарифмическая линейка:
У инженера и астронома не было
Инструмента полезнее, чем она.
Даже изящные искусства питаются ею.
Разве музыкальная гамма не есть
Набор передовых логарифмов?
И таким образом абстрактно красивое
Стало предком одного из величайших
Человеческих достижений”.
Були поети, які не присвячували оди експоненті та логарифмам, але згадували їх в своїх віршах. Наприклад, в своєму вірші “Фізики і лірики” поет Борис Слуцький
Б.Слуцкий
Потому-то, словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.
Підведення підсумків роботи на уроці, аналіз одержаних оцінок, поради, зауваження, оголошення переможців
VII. Домашнє завдання
Математика: Підручник \О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов, А.К. Сліпенко. – К.: Вища шк., 2001 – 447с. § 1.4 с. 259.
|
Обов’язкова частина |
Додаткове завдання |
|
|
|
|
Число 7 представити за допомогою трьох двійок і математичних символів. |
|
|
|
Додатки
Варіанти можливих презентацій
Історія виникнення логарифмів
- Винахід логарифмів на початку XVII ст. тісно пов'язаний з розвитком в XVI ст. виробництва і торгівлі, астрономії і мореплавання, що вимагали удосконалення методів обчислювальної математики. Все частіше потрібно було швидко проводити громіздкі дії над числами, все точніше і точніше повинні були бути результати дій. Ось тоді-то і знайшла втілення ідея логарифмів, цінність яких полягає в зведенні складних дій до найпростіших.
- В середині XVI ст. Симон Стівен опублікував таблицю для обчислення складних відсотків, необхідність яких була викликана зростанням торговельно-фінансових операцій. Сам Стівен не помітив того, що його таблицями почали користуватися для спрощення обчислень. Це побачив один з його сучасників – Бюрги. Талановитий математик І. Бюрги не був професійним ученим. Він був майстерним годинним майстром і механіком. У 1603 р. на запрошення імператора Рудольфа II він прибув до Праги, де став придворним годинникарем. Його перебування в Празі співпало за часом з перебуванням там Іоганна Кеплера. Діяльність Бюрги була високо оцінена Кеплером, який призвав Бюрги опублікувати свої винаходи. Бюрги склав таблицю логарифмів, де одних множень громіздких чисел на 1,0001 довелося проводити понад 200 млн разів. Бюрги не поспішав здати в друк свою працю, і лише в 1620 р. вона була опублікована.
- Слово ЛОГАРИФМ походить від грецьких слів - число и - відношення
- Проте найважливішою причиною обмеженого успіху таблиці Бюрги було те, що ще за 6 років до її публікації з'явилася досконаліша таблиця логарифмів Джона Непера. Складанню таблиць Непер присвятив близько 20 років свого життя. Таблиця Непера зіграла величезну роль в математичній науці.
- 6)Таблиці натуральних логарифмів склав і видав в 20-х роках XVII в Джон Спейдель.
7) Едмонт Гунтер в 1624 році, через 10 років після появи перших таблиць, винайшов логарифмічну лінійку. Протягом 300 років вона удосконалилася, але тільки в XX столітті набула широкого поширення, зараз її витиснули мікрокалькулятори і комп'ютери. Вона стала робочим інструментом для багатьох поколінь.
8)Тепер ми можемо знаходити значення логарифмів, використовуючи комп’ютер. Так, мовою программування PASCAL за допомогою стандартних функцій можна обчислювати натуральні логарифми чисел:
Program logaryfm;
Var x,y:real;
Begin
Read(x);
y:=ln(x);
Write(y);
End.
Логарифмічна спіраль.
1)Літак, що вилетів з якої-небудь точки земної кулі на північ, через деякий час опиниться над Північним полюсом. Якщо ж він полетить на схід, то, облетівши паралель, повернеться в той же пункт, з якого вилетів. Припустимо тепер, що літак летітиме перетинаючи всі меридіани під одним і тим же кутом, відмінним від прямого, тобто тримаючись весь час одного і того ж курсу. Коли він облетить земну кулю, то потрапляє в точку, що має ту ж довготу, що і точка вильоту, але розташовану ближче до Північного полюса. 2) Після наступного обльоту він виявиться ще ближчим до полюса і, продовжуючи летіти вказаним чином, описуватиме навколо полюса спіраль, що звужується.
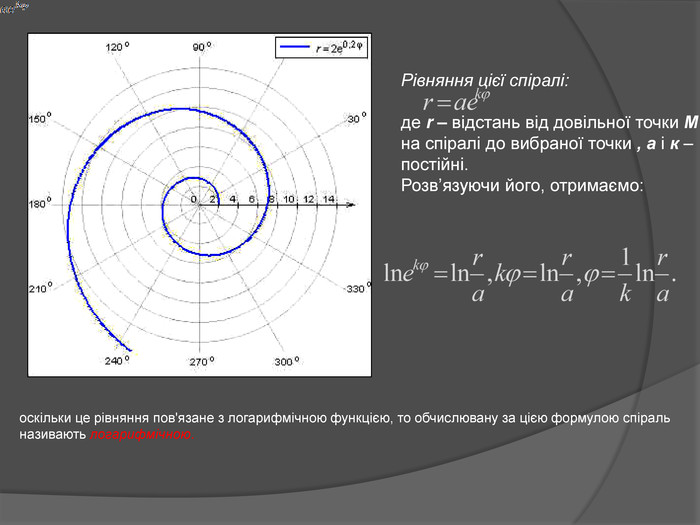
3)Рівняння цієї спіралі:
r = ![]() ,
,
гед r – відстань від довільної точки М на спіралі до вибраної крапки , ![]() – кут між променем ОМ і вибраним променем Ох, а і к – постійні.
– кут між променем ОМ і вибраним променем Ох, а і к – постійні.
Розв’язуючи його, отримаємо:![]() ,
, ![]()
оскільки це рівняння пов'язане з логарифмічною функцією, то обчислювану за цією формулою спіраль називають логарифмічною.
4)Живі істоти зазвичай ростуть, зберігаючи загальний контур своєї форми. При цьому вони ростуть на всіх напрямках – доросла істота і вище і товстіша за дитинча. Але раковини морських тварин можуть рости лише в одному напрямі. Щоб не дуже витягуватися в довжину, їм доводиться скручуватися, причому кожен наступний виток подібний до попереднього. А таке зростання може здійснювати лише по логарифмічній спіралі або її деяким просторовим аналогам.
- Тому раковини багатьох молюсків, равликів, а також роги таких ссавців, як архари (гірський козел), закручені по логарифмічній спіралі.
- Один з найбільш поширених павуків – епейра, сплітаючи павутиння, закручує нитки навколо центру по логарифмічній спіралі
Можна сказати, що ця спіраль є математичним символом співвідношення форм зростання. Великий німецький поет Іоганн Вольфгант Гете вважав її навіть математичним символом життя і духовного розвитку.
- 8) 9) 10)По логарифмічній спіралі формується і тіло циклона, а також
закручено і багато галактик, зокрема, Галактика, якій належить Сонячна система.
11) Одна з чудових властивостей логарифмічної спіралі полягає в тому, що довільний промінь, що виходить з її полюса, перетинає будь-який виток спіралі під одним і тим же кутом. Ця властивість застосовується в ріжучих машинах. Ножі соломорізки, що обертаються, мають профіль, обкреслений по логарифмічній спіралі. Кут різання такого механізму постійний уздовж всієї кромки рухомого ножа.
Виявляється, трубу, що підводить струмінь води до лопастей турбінного колеса на гідроелектростанції, також слід завертати по логарифмічній спіралі. Тоді втрати енергії рухомої води будуть мінімальними.
12)Логарифмічна спіраль – крива «з твердим характером». Вона не змінює своєї природи при багатьох перетвореннях, до яких чутливі інші криві. Стиснути або розтягнути цю спіраль щодо її полюса – те ж саме, що повернути її на певний кут. Властивості логарифмічної спіралі так глибоко вразили швейцарського математика Якоба Бернуллі, що він заповів висікти її на своєму надгробку, що супроводжує зображення латинською фразою «Eadem mutata resurgo» - «Змінена, відроджуюся колишньою».
Зірки, шум і логарифми
1)Тут, здавалося б, пов’язані несумісні речі . Шум і зірки об'єднуються тому, що гучність шуму і яскравість зірок оцінюються однаковим чином – за логарифмічною шкалою. 2)Астрономи ділять зірки за степенем яскравості на видимі і абсолютні зоряні величини – зірки першої величини, другої, третьої і так далі Послідовність видимих зоряних величин, що сприймаються оком, є арифметичною прогресією. Але фізична їх яскравість змінюється за іншим законом: яскравості зірок складають геометричну прогресію із знаменником 2,5. Легко зрозуміти, що «величина» зірки є логарифмом її фізичної яскравості. Оцінюючи яскравість зірок, астрономи оперують таблицею логарифмів, складеною за основою 2,5.
3) Аналогічно оцінюється і гучність шуму. Шкідливий вплив промислових шумів на здоров'я робочих і на продуктивність їх праці спонукало виробити прийоми точної числової оцінки гучності шуму. Одиницею гучності служить «бел», але практично використовуються одиниці гучності, що = його десятій частині, - так звані «децибели». Послідовність степеня гучності 1 бел, 2 бели і так далі складають арифметичну прогресію. Фізичні ж величини, що характеризують шуми (енергія, інтенсивність звуку і ін.), складають геометричну прогресію із знаменником 10. Гучність, виражена в белах, дорівнює десятковому логарифму відповідної фізичної величини. 4) Розглянемо декілька прикладів: тихе шелестіння листя оцінюється в 1 бел, гучна мова – в 6,5 белів, гарчання лева – в 8,7 белів, шум Ніагарського водопаду – 9 белів. 5) Звідси випливає, що по силі звуку розмовна мова перевищує шелестіння листя в 1 млн 316 тис разів, левове гарчання сильніше гучної мови в 158 разів.
6)Логарифми і відчуття
Відчуття, що сприймаються органами чуття людини, можуть викликатися роздратуваннями, що відрізняються один від одного в багато мільйонів і навіть мільярдів разів. Удари молотка об слизьку плиту в сто разів голосніші, ніж тихе шелестіння листя, а яскравість дуги вольта в трильйони разів перевершує яскравість якої-небудь слабкої зірки, ледь помітної в нічному небі. Але ніякі фізіологічні процеси не дозволяють дати такого діапазону відчуттів. Досліди показали, що організм як би «логарифмує» отримані ним роздратування, тобто величина відчуття приблизно пропорційна десятковому логарифму величини роздратування. Як бачимо, логарифми застосовуються і в психології.
Музика, живопис, архітектура і логарифми.
Розкопуючи одне з поселень кам'яного віку на території України, археологи виявили декілька кісток мамонта, призначення яких було їм не зрозуміле. Уважний аналіз показав, що на цих кістках залишалися сліди ударів – це були залишки шумового оркестру, під звуки якого в давнину здійснювалися магічні танці. Звучання тятиви лука навело на думку про створення струнних інструментів.
Піфагор був не тільки великим математиком, але і хорошим музикантом. Він встановив, що приємні поєднання звуків відповідають певним співвідношенням між довжинами струн, що коливаються, і відстанню між дірочками сопілки; створив першу математичну теорію музики. 1)Хоча музиканти не люблять перевіряти алгеброю гармонію, вони весь час мають справу з математикою, оскільки сучасна альфа заснована на логарифмах. Розглянемо приклад – «гра на роялі». Номери клавішів на роялі є логарифмами чисел коливань відповідних звуків; номер октави є характеристикою, а номер звуку в даній октаві мантисою цього логарифма.
- 2) Відомий фізик Ейхенвальд пригадував: «товариш мій з гімназії полюбляв грати на роялі, та не любив математики. Він навіть говорив , що музика і математика не мають нічого спільного. Уявіть же собі, як неприємно був вражений мій товариш , коли я довів йому, що, граючи на клавішах сучасного роялю, він грає на… логарифмах»
3)Дійсно, сходинки хроматичної гами(12-звукової) частот звукових коливань представляють собою логарифми. Тільки основа цих логарифмів = 2 (а не 10, як в інших випадках). Припустимо, що ноті «до» - відповідає частота = n коливанням в секунду. В октаві частота коливань нижнього звука в два рази менша верхнього, тобто ці частоти відносяться як 1: 2. Тоді ноті «до» першої октави відповідають 2n коливань в секунду. Позначимо всі ноти хроматичної гами номерами p.
4) Тоді частота звука вира-жається формулою
Npm = n * 2m (√2)p
Логарифмуючи, отримаємо
lg Npm=lg n+ mlg 2 + plg2/12
lg Npm= lg n + (m +γ/12) lg2
- Приймаючи частоту «до» за 1 (n = 1) і зводячи всі логарифми до основи 2, маємо
log2 Npm = m + γ/12
Логарифмічні лінії в природі помічають не тільки математики, але і художники, наприклад, це питання хвилювало Сальвадора Далі.
- Його нав’язливою ідеєю стала картина Вермеєра «Мереживниця», репродукція якої висіла в кабінеті батька. Пізніше Сальвадор Далі попросив в Луврі дозволу написати копію з цієї картини, а потім кіномеханіка показати на екрані репродукцію намальованої копії. Він пояснив, що, поки не написав копію, майже нічого не розумів в «Мереживниці», і йому знадобилося ціле літо, щоб нарешті зрозуміти, що він інстинктивно провів на полотні строгі логарифмічні криві.6)
7)Логарифмічну спіраль можно побачити і в архітектурі. Прикладом є вежа в Москві.
№1
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]()
№2
а) ![]() ;
;
б) ![]()
в)![]()
г)![]()
№3
а) ![]()
б) ![]()
в) ![]()
г)![]() .
.
№4
а) ![]()
б) ![]()
в) ![]()
г)![]()
Заповіт на сотні років
Відомий заповіт знаменитого американського державного діяча Бенджамина Франкліна. Ось уривок з нього.
«Доручаю тисячу фунтів стерлінгів жителям Бостона. Якщо вони приймуть цю тисячу фунтів, то повинні доручити її добірним громадянам, а вони даватимуть їх з відсотками, по5 на сто в рік, в позику молодим ремісникам. Сума ця через сто років збільшиться до 131000 фунтів стерлінгів. Я бажаю, щоб тоді 100000 фунтів було спожито на споруду громадських будівель, останні ж 31000 фунтів була віддана у відсотки на 100 років. По закінченню другого століття сума зросте до 4060000 фунтів стерлінгів, з яких 1060000 фунтів залишаю в розпорядження жителів Бостона, а 3000000 – правлінню Массачусетської спільноти. Далі не насмілююся простягати своїх видів».
Залишаючи всього 1000 фунтів, Франклін розподіляє мільйони. Математичний розрахунок показує, що міркування


про публікацію авторської розробки
Додати розробку